小學生幾何直觀能力的培養策略

張衛星

《義務教育數學課程標準（2011年版）》指出：幾何直觀主要是指利用圖形描述和分析問題;借助幾何直觀可以把復雜的數學問題變得簡潔、形象，有助于探索解決問題的思路，預測結果;幾何直觀可以幫助學生直觀地理解數學，在整個數學學習過程中都發揮著重要作用。筆者認為，幾何直觀是利用圖形洞察問題本質的一種方式，它既有形象思維的特點，又有抽象思維的特點。如果能夠將幾何直觀作為一種重要的方法、思想滲透于日常教學中，就能幫助學生理解數學知識，提高解決問題的能力。那么，如何在數學教學中培養小學生的幾何直觀能力呢？

一、以形譯數，讓抽象的數變直觀

按照雙重編碼理論，造成數學知識學習和記憶困難的主要原因在于數學學習材料（數學語言和符號）具有高度的抽象性，它不容易喚起視覺印象。因此，在小學數學教學中應該重視對學生進行心理印象方面的訓練。即在知識的形成階段，充分利用數學學習材料數與形統一的特點，引導學生將數學知識的言語表征轉化為表象表征，將數譯成形，形成科學、合理的概念系統。

如，一位教師教學“認識一位小數”時，就特別強調將數的意義通過直觀的形式表現出來。教師先后組織了三個層次的活動，引導學生將數譯成形。第一個層次，讓學生用語言描述0.1的含義，既激發了學生對0.1的已有認識，又為下面畫圖表示0.1做了必要的準備。第二個層次，讓學生在表示整數“1”的正方形中分一分、涂一涂，表示出0.1的大小，再用語言描述所畫圖的含義。結果，學生有4種表示方法，即把正方形平均分成10行，涂其中的一行;把正方形平均分成10列，涂其的一列;把正方形平均分成5行2列，涂其中的一份;把正方形平均分成兩行5列，涂其中的一份。如果把這四種方法進行歸類，實質上是兩種表示方法（如圖1、圖2）。

圖1 ? ? ? 圖2

第三個層次，引導學生借助一個被平均分成10份的長方形，涂色表示出其他的“零點幾”，并由此歸納一位小數的含義。這樣以形譯數，把抽象的數變得直觀可見，既幫助學生理解了一位小數的意義，又有利于學生積累更豐富的用圖形表征數學概念的經驗。更為重要的是增強了學生的數感，發展了他們的幾何直觀能力。

二、以形譯式，讓抽象的式變直觀

在小學數學中，有相當一部分數學知識都是伴隨著幾何意義而存在的。教師在數學課堂教學中加強數學知識幾何意義的闡釋，有利于學生形成知識表象，促進對數學知識的理解和記憶，積累表象建構的經驗，同時也為問題解決過程中的表象遷移提供了潛在的可能。特別是對于一些難以用語言表達的抽象算式，如果能用直觀的圖形表示出來，就可以讓抽象的算理變得通俗易懂，從而讓學生輕松學會。

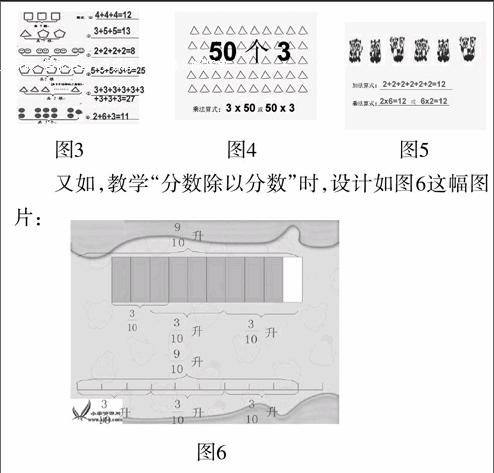
如，教學“乘法的初步認識”時，首先引導學生用加法式子表示各種圖形的的含義（如圖3），然后利用圖4讓學生感受列加法算式比較麻煩，從而想到用簡潔的算式，即乘法算式來表達。最后，利用圖5來溝通直觀圖形、加法算式、乘法算式之間的聯系。

這樣教學，就為學生主動建構乘法意義的表象提供了豐富的素材，加深了學生對乘法意義的理解，式與形實現了完美統一，使學生初步獲得了利用圖形直觀描述數學知識的經驗。

圖3 ? ? ? 圖4 ? ? ? 圖5

又如，教學“分數除以分數”時，設計如圖6這幅圖片：

圖6

當學生理解了這幅圖的含義，對于÷=3的理解也就水到渠成。可見，根據學生的特點適度以形譯式，可能會取得意想不到的效果。

三、以形譯形，讓抽象的形變直觀

小學生的空間觀念薄弱，主要因為他們年齡小，知覺水平尚處于低級階段，抽象思維能力相對較弱。學生初次接觸的幾何圖形是從整體上認識的，不會關注圖形的細節，是一種照相機式的認識方法。他們難以對圖形進行合理地想象，難以正確地理解圖形的內涵。因此，小學生學習幾何需要更多的經驗，通過觀察比較，獲得對圖形豐富的感性認識，從而較好地把握圖形的本質特征。

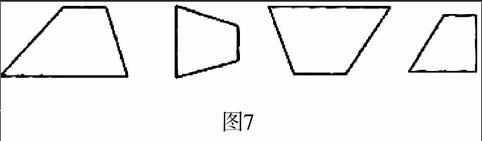
如，教學“認識梯形”時，教師設計了如下的一組圖形（如圖7），讓學生辨認。

圖7

這樣通過位置變換，讓學生認識在不同位置狀態下的梯形，學生對梯形的認識就會全面而深刻。

又如，在學生學完“長方形和正方形的周長”后，設計如下一道習題：

兩個完全一樣的長方形，長4厘米，寬3厘米。如果將這兩個圖形拼成一個新的大長方形，這個新的大長方形的周長至少是多少厘米？

學生的認識比較膚淺，初做這道題，全班同學幾乎“全軍覆沒”，他們都是先求出一個長方形的周長，然后再將這個周長乘2就是大長方形的周長。為此，教師利用課件展示如下兩種拼的結果（如圖8、圖9）：

圖8

圖9

在這兩個直觀圖形的參照下，學生經過思考、交流、討論，最后算出圖8的周長是22厘米，圖9的周長是20厘米。在此基礎上，教師再讓學生說說為什么這兩個大長方形周長會不一樣。學生通過觀察知道，圖8減少了兩條寬，而圖9減少了兩條長，因此周長不一樣。至此，學生也就明白“至少”的含義。

上述這兩個例子帶給我們的啟示是：想讓學生牢固把握幾何圖形的內涵，就應當重感知、重體驗、重理解，用圖形的直觀幫助學生理解圖形的本質。

四、以形譯聯，讓抽象的聯變直觀

盡管不同數學知識的內涵不同，但它們之間卻并非毫無聯系。不要把幾何直觀簡單地等同于能用圖形描述問題的技能，幾何直觀更為深遠的意義表現為能夠借助圖形去分析知識之間的聯系，從而讓學生建立正確的、穩固的知識結構。因此，當學生遇到一些難以厘清的相關概念之間的關系時，教師要適時以形譯聯，讓抽象的知識變得更直觀。如，教學“長方形和正方形的關系”時，學生常會說“長方形是特殊的正方形”，究其原因是學生沒有厘清兩者的關系。為此，教師應引導學生一起畫韋恩圖（如圖10）：