三維斜流線性完全耦合層吸收邊界條件

伍　新　陳志夫　尹漢鋒

1.湖南大學汽車車身先進設計制造國家重點實驗室，長沙，4100822.湖南工程學院，湘潭，4111043.廣州汽車集團股份有限公司汽車工程研究院，廣州，511434

三維斜流線性完全耦合層吸收邊界條件

伍新1,2陳志夫3尹漢鋒1

1.湖南大學汽車車身先進設計制造國家重點實驗室，長沙，4100822.湖南工程學院，湘潭，4111043.廣州汽車集團股份有限公司汽車工程研究院，廣州，511434

采用傅里葉與拉普拉斯變換方法分析了三維斜流背景下聲波、渦波與熵波的色散關系；根據各物理波的色散軌跡特征，結合頻率變化的時空坐標變換方法，給出了一組時間與空間坐標變換關系式，并將三維斜流線性歐拉方程變換至新坐標系；采用復數變換方法，引入阻尼，分別構建了x層、y層、z層及角層的完全耦合層(PML)吸收邊界條件,給出了吸收項的施加原則；最后通過三維脈沖聲波、對稱渦環與周期性點聲源在斜時均流中的傳播問題驗證了該吸收邊界條件的正確性。研究結果表明：所提出的坐標變換關系能夠有效解決各物理波相位速度與群速度不一致的問題；在斜背景流下，該PML吸收邊界條件能較好地吸收物理波，有效抑制邊界反射，可用于氣動聲學計算。

完全耦合層；邊界條件；計算氣動聲學；歐拉方程；色散

0　引言

在開放區域氣動聲學問題的數值計算中，無限計算域需要人工截斷，形成一種特殊的邊界條件，即無反射邊界條件，它既要使計算域內的各種物理波能無反射或者較小反射地通過邊界，又能讓計算域外的物理波能順利通過邊界進入計算域，同時，還能阻止計算域外的非物理波傳入計算域。完全耦合層(perfectly matched layer,PML)吸收邊界條件作為最優秀的無反射邊界條件之一，在近年取得了極大的發展。

文獻[1-5]首次將Berenger提出的PML技術引入計算氣動聲學領域，提出了一系列穩定的PML吸收邊界條件。Lin等[6]建立了一個適用于平行流計算的非線性和黏性PML吸收邊界條件。結合譜差分方法，Zhou等[7]采用該黏性PML吸收邊界條件求解了圓柱繞流等典型氣動聲學問題。柳占新等[8]從聲學角度推導了笛卡兒坐標系和柱坐標下全歐拉方程的PML吸收邊界條件，并將其應用于渦扇發動機進氣道流場模擬。周正干等[9]應用PML技術分析了超聲波聲場特性。Parrish等[10-11]通過兩次坐標變換，提出了穩定的二維線性和非線性斜流PML吸收邊界條件，并將其拓展至圓柱坐標系。雖然上述PML吸收邊界條件具有較高的數值精度，但是，它們無法求解三維任意方向入流問題。

在汽車側風、圓柱或鈍體斜向繞流等氣動聲學問題的數值計算中，往往存在背景斜流。斜流使流場內各物理波的群速度與相位速度方向不同，這給穩定的PML構造帶來了挑戰，即如何建立正確的坐標轉換關系[12]。針對該問題，本文從控制方程內各物理波的色散關系軌跡出發，構建恰當的坐標轉換關系，修正各物理波的群速度與相位速度方向，發展三維斜流線性PML吸收邊界條件。

1　控制方程色散關系分析與坐標變換

1.1控制方程

笛卡兒坐標系下，三維量綱一斜流線性歐拉方程為

(1)

其中，ρ為密度，u、v、w分別為x、y、z方向的速度，Max、May、Maz分別為x、y、z方向的馬赫數，p為壓力，H為非定常源項。

1.2色散關系分析

根據波數分析理論，對式(1)等號兩邊進行傅里葉與拉普拉斯變換：

(2)

其中，ω為頻率，kx、ky、kz分別為x、y、z方向的波數。經該變換后即可獲得三維斜流線性歐拉方程的色散關系矩陣Ψ：

(3)

λ=ω-Maxkx-Mayky-Mazkz

通過求解色散關系矩陣Ψ的零點λi(i=1,2,…,5)即可獲得各物理波的色散關系。熵波與渦波的色散關系為

ω-Maxkx-Mayky-Mazkz=0

(4)

聲波的色散關系為

(5)

為了分析各物理波的群速度與相位速度方向，將式(4)與式(5)等號兩邊同時除以頻率ω，得

(6)

(7)

渦波、熵波及聲波在坐標系(kx/ω,ky/ω,kz/ω)內的色散關系軌跡如圖1a所示。圖1a中，渦波與熵波的色散關系軌跡為一個斜置的平面，聲波的色散關系軌跡為一個中心不在坐標系原點的斜置橢球。根據色散關系軌跡穩定性分析方法[13]，三維斜流線性歐拉方程中，不論是渦波、熵波還是聲波，其色散關系軌跡均存在不穩定區域，因此，在進行PML變換之前，必須采用適當的坐標變換來修正域內各物理波的群速度與相位速度方向。

1.3坐標變換關系的構建

如果將z方向的斜流消去，則該問題可以轉化為二維斜流線性歐拉方程的坐標變換關系式的推導。參考文獻[13]中的結論，x層坐標變換的關系式可以表示為

(8)

式中，t為時間。

由式(8)可獲得各物理量關于新坐標與原坐標偏導數之間的關系:

(9)

與式(9)相對應的新波數、新頻率與原波數、原頻率之間的關系為

(10)

(11)

聲波的色散關系為

(12)

同理，可以獲得用于y層與z層PML吸收邊界條件推導的坐標變換關系式，其表達式分別為

(13)

(14)

(a)變換前(b)x層

(c)y層(d)z層圖1　物理波在坐標系(kx/ω,ky/ω,kz/ω)與內的色散關系軌跡

2　PML吸收邊界條件推導

采用復數變換方法，通過式(8)、式(13)與式(14)分別推導x層、y層及z層的PML吸收邊界條件。然后，根據各層PML吸收邊界條件推導各角層PML吸收邊界條件。對于三維計算域，整個計算域由26塊PML吸收域與一個物理計算域組成，PML吸收邊界條件由七大部分組成，分別為x層、y層、z層、xy層、yz層、xz層及xyz層，如圖2所示。

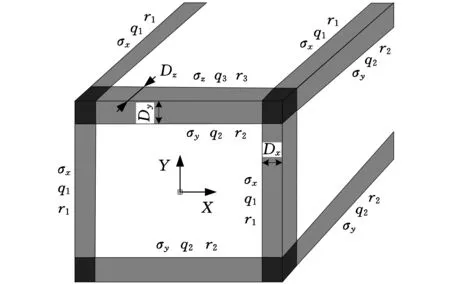
圖2　物理域與PML計算域示意圖

2.1平行層PML吸收邊界條件

首先，將式(9)代入式(1)，將控制方程變換至新坐標系：

(15)

其次，引入阻尼，將新時間、空間坐標系下的控制方程轉換至頻域：

(16)

再次，引入輔助變量q1，將頻域PML吸收邊界條件變換至新的時間與空間坐標系：

(17)

(18)

最后，通過式(9)將新時間、空間坐標系下的PML吸收邊界條件變回至原時間與空間坐標系，獲得x層PML吸收邊界條件：

(19)

(20)

同理，也可獲得y層與z層PML吸收邊界條件：

(21)

(22)

(23)

(24)

2.2角層PML吸收邊界條件

關于xy層PML吸收邊界條件，吸收系數σx與σy均不為零，因此結合x層和y層PML吸收邊界條件即可得xy層PML吸收邊界條件，其表達式為

(25)

(26)

(27)

為了使xy層PML吸收邊界條件穩定，在輔助變量方程(式(26)與式(27))等號左邊，分別增加額外的吸收項σyq1與σxq2，該吸收項對穩定性的影響詳見文獻[13]。

同理，也可獲得yz層和xz層PML吸收邊界條件，其表達式分別為

(28)

(29)

(30)

(31)

(32)

(33)

為使各角層PML吸收邊界條件穩定，在式(29)、式(30)、式(32)與式(33)等號的左邊依次增加吸收項σzq2、σyq3、σzq1與σxq3。

關于xyz層PML吸收邊界條件，吸收系數σx、σy與σz均不為零，因此必須結合x層、y層和z層PML吸收邊界條件即可得xyz層PML吸收邊界條件，其表達式為

[σx(I+βxA)+σy(I+βyB)+σz(I+βzC)]u=0

(34)

(35)

(36)

(37)

式(35)～式(37)中，(σy+σz)q1、(σx+σz)q2與(σx+σy)q3分別為輔助變量方程中額外增加的吸收項。

3　算例驗證

為驗證本文構建的三維斜流線性PML吸收邊界條件的正確性，選用三維脈沖聲波、對稱渦環與周期性點聲源在斜時均流中的傳播問題作為測試算例。計算域四周均采用PML吸收邊界條件，空間離散格式采用改進的7點色散保持有限差分格式[13]，時間推進格式采用6級4階低耗散低色散RK顯式格式[14]。為了消除短波對數值計算的影響，采用人工黏性耗散[15]進行計算。計算時空間網格尺寸Δx=Δy=Δz=1，時間步長取0.1 s，吸收系數σx、σy、σz分別為

(38)

D為PML吸收寬度，xb、yb、zb分別為PML計算域與歐拉計算域的交界位置，根據文獻[10]，σm、α分別取值2、3。

3.1脈沖聲波傳播

假定該脈沖聲波初始位置在坐標原點，并且處于速度場為(0.5,0.5,0.5)的時均流場中，該問題的初始條件可描述為

(39)

設該問題的歐拉計算域為x,y,z∈[-20,20]，吸收寬度取值為D=10Δx=10Δy=10Δz，在t=40 s時的壓力等值面及截面等值線如圖3所示。可以看出，當三維脈沖聲波達到PML吸收邊界時，聲波迅速衰減，在邊界處未見明顯反射。

(a)壓力等值面圖(b)平面z=20上的壓力等值線圖圖3　t=40 s時壓力圖

3.2渦環傳播

渦環動力學及其發聲機理是目前一個非常活躍的研究方向，也是理論流體力學與氣動聲學領域中的難點。以對稱渦環在斜時均流中的傳播問題作為測試算例進行測試。設渦環的半徑r0=10，渦核的半徑b=3，初始時刻渦環對稱中心位于坐標系原點，將該渦環置于(0.5,0.5,0.5)的時均流場中，如圖4所示，該問題的初始條件可描述為

(40)

ux(r)=εr0r-1(r-r0)e-α[x2+(r-r0)2]

ur(r)=-εr0r-1(r-r0)xe-α[x2+(r-r0)2]

圖4　對稱渦環示意圖

采用與3.1節中相同的計算方案，獲得渦量隨時間的變化情況，如圖5所示。該渦環隨時均流對流，可以看出，當渦環到達PML計算域內時，渦量迅速衰減，且未見明顯反射。由此可知，當任意方向斜流存在時，渦環能順利穿過計算邊界，該PML吸收邊界條件能較好地吸收渦環中的物理波。

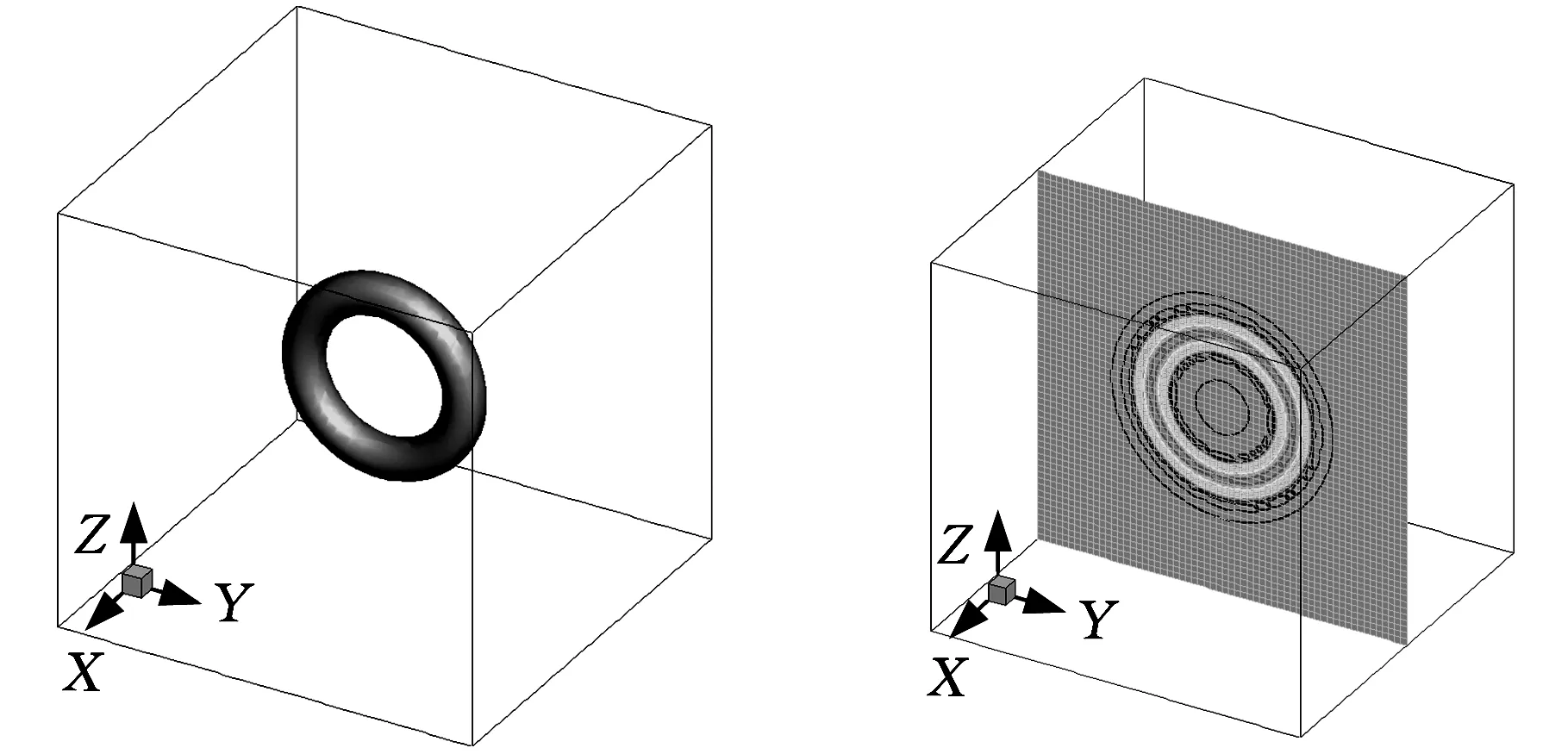
(a)t=0時渦量等值面圖(b)t=0時平面x=0上的渦量等值線圖

(c)t=40 s時渦量等值面圖(d)t=40 s時平面x=20上的渦量等值線圖圖5　渦量隨時間變化圖

3.3周期性點聲源傳播

為了測試PML吸收邊界條件對周期性聲波的吸收性能，在式(1)中的壓力方程右端施加一個周期性點聲源，該點聲源為

s(x,y,z,t)=sin(0.2πt)e-(ln2)[x2+y2+z2]/32

(41)

歐拉計算域為x,y,z∈[-40,40]，計算域外圍采用10層PML吸收邊界條件。

當t=100s時，壓力數值解等值面與等值線如圖6所示。可以看出，周期性聲波能無反射地通過邊界。

(a)聲壓等值面圖(b)平面x=0上的聲壓等值線圖

(c)平面y=0上的聲壓等值線圖(d)平面z=0上的聲壓等值線圖圖6　t=100 s時聲壓等值面與等值線圖

4　結論

(1)三維斜流線性歐拉方程中，渦波、熵波與聲波的色散關系軌跡均存在不穩定區域。

(2)提出的坐標變換關系式能有效修正各物理波的群速度與相位速度方向，使其色散關系軌跡均穩定。

(3)提出的PML吸收邊界條件能較好地吸收熵波、渦波與聲波，未見明顯反射。

[1]BerengerJP.APerfectlyMatchedLayerfortheAbsorptionofElectromagneticWaves[J].JournalofComputationalPhysics, 1994, 114(2): 185-200.

[2]HuFQ.OnAbsorbingBoundaryConditionsforLinearizedEulerEquationsbyaPerfectlyMatchedLayer[J].JournalofComputationalPhysics, 1996, 129(1): 201-219.

[3]HuFQ.AStablePerfectlyMatchedLayerforLinearizedEulerEquationsinUnsplitPhysicalVariables[J].JournalofComputationalPhysics, 2001, 173(2): 455-480.

[4]HuFQ.APerfectlyMatchedLayerAbsorbingBoundaryConditionforLinearizedEulerEquationswithaNon-uniformMeanFlow[J].JournalofComputationalPhysics, 2005, 208(2): 469-492.

[5]HuFQ,LiXD,LinDK.AbsorbingBoundaryConditionforNonlinearEulerandNavier-stokesEquationsBasedonthePerfectlyMatchedLayerTechnique[J].JournalofComputationalPhysics, 2008, 227(9): 4398-4424.

[6]LinDK,LiXD,HuFQ.AbsorbingBoundaryConditionforNonlinearEulerEquationsinPrimitiveVariablesBasedonthePerfectlyMatchedLayerTechnique[J].Computers&Fluids, 2011, 40(1): 333-337.

[7]ZhouY,WangZJ.AbsorbingBoundaryConditionsfortheEulerandNavier-stokesEquationswiththeSpectralDifferenceMethod[J].JournalofComputationalPhysics, 2010, 229(23): 8733-8749.

[8]柳占新, 高頻, 仝志勇.全歐拉方程的理想匹配層邊界條件[J].中國機械工程, 2011, 22(16): 1938-1941.

LiuZhanxin,GaoPin,TongZhiyong.PMLBoundaryConditionsforFullEulerEquations[J].ChinaMechanicalEngineering, 2011, 22(16): 1938-1941.

[9]周正干, 魏東.時域有限差分法在超聲波聲場特性分析中的應用[J].機械工程學報，2010, 46(2): 9-13.

ZhouZhenggan,WeiDong.AnalysisofUltrasonicSoundFieldCharacteristicwithFDTD[J].ChineseJournalofMechanicalEngineering，2010, 46(2): 9-13.

[10]ParrishSA,HuFQ.PMLAbsorbingBoundaryConditionsfortheLinearizedandNonlinearEulerEquationsintheCaseofObliqueMeanFlow[J].InternationalJournalforNumericalMethodsinFluids, 2009, 60(5): 565-589.

[11]ParrishSA.AnalysisandApplicationofPerfectlyMatchedLayerAbsorbingBoundaryConditionsforComputationalAeroacoustics[D].Norfolk:Univ.ofOldDominion, 2008.

[12]HuFQ.DevelopmentofPMLAbsorbingBoundaryConditionsforComputationalAeroacoustics:aProgressReview[J].Computers&Fluids, 2008, 37(4): 336-348.

[13]陳志夫.基于色散關系分析的高精度氣動聲學計算方法研究[D].長沙:湖南大學, 2013.

[14]HuFQ,HussainiMY,MantheyJL.Low-dissipationandLow-dispersionRunge-KuttaSchemesforComputationalAcoustics[J].JournalofComputationalPhysics, 1996, 124(1): 177-191.

[15]TamCKW,JayC,ZhongD.AStudyoftheShortWaveComponentsinComputationalAcoustics[J].JournalofComputationalAcoustics, 1993, 1(1): 1-30.

(編輯陳勇)

Three Dimensional Linear PML Absorbing Boundary Conditions with an Oblique Mean Flow

Wu Xin1,2Chen Zhifu3Yin Hanfeng1

1.State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Hunan University,Changsha,410082 2.Hunan Institute of Engineering,Xiangtan,Hunan,411104 3.Guangzhou Automobile Group Co.,Ltd. Automotive Engineering Institute,Guangzhou,511434

For three dimensional linear Euler equations in the case of oblique mean flow, the dispersion relations of acoustic, vortex and entropy wave were first analyzed by using Fourier and Laplace transform method. Then the hypothesis for changed frequency was employed, a proper space-time transformation was presented for deriving three dimensional linear Euler equations in transformed coordinates. A complex change was applied to the new equations and a damping parameter was introduced. A three linear PML absorbing boundary conditions in the case of oblique mean flow forxlayer,ylayer,zlayer and corner layer were derived. In addition, the importance of added absorption term was emphasized. Finally, the effectiveness of linear PML absorbing boundary conditions was validated by computing the computational aeroacoustics benchmark problems. The results prove that: the presented space-time transformation can solve the problem of direction inconsistence in group and phase velocity of physical wave; in the case of oblique mean flow, the proposed PML absorbing boundary conditions can absorb the physical wave with little or no reflection.Therefore,it also can be applied to aeroacoustic computation.

perfectly matched layer(PML); boundary condition; computational aeroacoustics; Euler equation; dispersion

2014-05-19

國家自然科學基金資助項目(11302075,11002052)；湖南省教育廳高等學校科學研究項目(12C0627)

V211.3DOI：10.3969/j.issn.1004-132X.2015.01.001

伍新，男，1976年生。湖南大學汽車車身先進設計制造國家重點實驗室博士研究生，湖南工程學院機械工程學院講師。主要研究方向為計算聲學、振動與噪聲控制。陳志夫，男，1986年生。廣州汽車集團股份有限公司汽車工程研究院工程師。尹漢鋒，男，1982年生。湖南大學汽車車身先進設計制造國家重點實驗室講師、博士。