從虛位移原理到拉格朗日方程

劉偉偉

（滄州師范學院物理與電子信息系，河北滄州　061001）

從虛位移原理到拉格朗日方程

劉偉偉

（滄州師范學院物理與電子信息系，河北滄州061001）

由虛位移原理出發(fā)結合達朗貝爾原理得到動力學普遍方程，再有這個普遍方程得到拉格朗日方程。容易看出理論力學比經(jīng)典力學有更深的理論基礎和靈活性。尤其是廣義坐標、廣義力的引入，以能量為基本概念的動力學方程比牛頓第二定律更具有理論優(yōu)勢。通過方程的應用實例可揭示出這兩個方程在分析力學中具有非常重要的理論價值和應用價值。

廣義坐標廣義力虛位移拉格朗日方程

分析力學是理論力學的重要組成部分，它給出了與牛頓第二定律等價的力學基本方程，提供了解決力學問題的不同方法，拉格朗日方程也是分析力學中一個重要的基本方程。拉格朗日方程是在動力學的普遍方程（達朗伯—拉格朗日方程）的基礎上，將各點的坐標xi 、及其虛位移變換為δxi廣義坐標qj及其變分δqj后得到的。為了加深對拉格朗日方程的認識和理解，以便能更好地運用它來分析和解決問題，下面將達朗伯原理和虛位移原理結合起來推導出動力學普遍方程和拉格朗日方程。

1　從虛位移原理動力學普遍方程

設由n個質(zhì)點組成的質(zhì)點系，由達朗伯→原理知，在質(zhì)點→系運動的任一→瞬時，任一質(zhì)點Mi上作用的主動力，約束反力及其慣性力三者構成形式上的平衡力系，即：

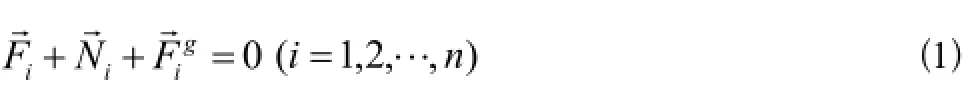
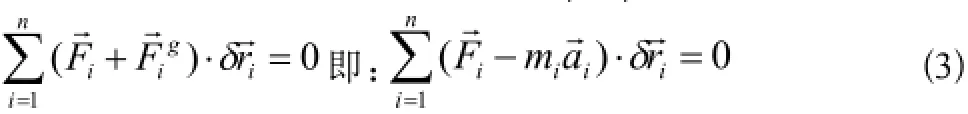
（3）式是通過達朗伯虛加慣性力手段和虛位移原理相結合而得到的結果，稱為動力學普遍方程，也稱達朗伯——拉格朗日方程。

2　從動力學普遍方程到拉格朗日方程

由分析力學，可設主動力為F=（F1，F(xiàn)2，···，F(xiàn)n），廣義力Q=（Q1，Q2，···QN）

如果將位矢對任意一個廣義坐標 qj求偏導數(shù)，再對時間求導數(shù)，則得到

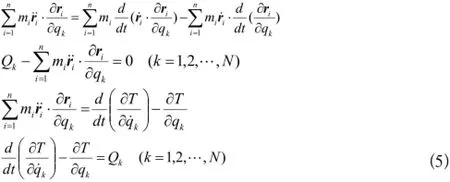
如果作用在系統(tǒng)上的主動力都是有勢力，根據(jù)有勢力的廣義主動力

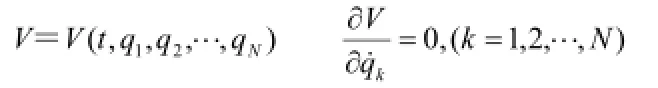
引入拉格朗日函數(shù)L=T－V，T是動能，V是勢能，得到主動力為有勢力的拉格朗日方程

動力學普遍方程中系統(tǒng)的運動是直角坐標來描述的，而拉格朗日方程是用廣義坐標來描述系統(tǒng)的運動，兩者都可用來解決非自由質(zhì)點系的動力學問題，對于解決復雜的非自由質(zhì)點系的動力學問題，應用拉格朗日方程往往要比用動力學普遍方程簡便得多。

3　應用舉例

為了說明分析力學在解決力學問題靈活、方便且科學上的嚴謹?shù)葍?yōu)勢，我們可通過以下面例題的求解來彰顯。

如圖1所示，試用拉格朗日方程求單擺的微振動方程和周期。

解：設單擺的擺長為l，擺錘質(zhì)量為m，取θ為廣義坐標，則拉格朗日函數(shù)為：

在解題過程中，并沒有用大家所熟悉的牛頓第二定律與拉格朗日方程對比來求解。但仍能明顯的感覺到，用分析力學解題比用牛頓第二定律的方法簡單靈活的多。

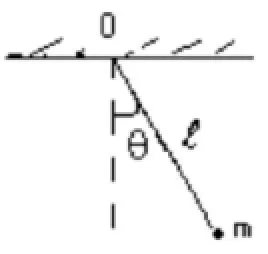
圖1　

4　結語

在分析力學中，關于力學系統(tǒng)的動力學規(guī)律有兩種不同的表述，其中之一便是拉格朗日表述，在這種表述中，就是用拉格朗日方程來描述系統(tǒng)的運動規(guī)律。

拉格朗日方程的基本特色在于：（1）由于采用廣義坐標作基本變量，微分方程式的數(shù)目和系統(tǒng)的自由s度數(shù)目相同，微分方程的數(shù)目是最少的。（2）由于微分方程中不包含約束反力，以及所使用的函數(shù)（動能函數(shù)、勢能函數(shù)等）多為標量函數(shù)，這和牛頓的力學方程相比較，在解決質(zhì)點系動力學問題時有很大的優(yōu)越性。（3）第二類拉格朗日方程是力學系統(tǒng)在具有最一般意義的廣義坐標描述下保持形式不變的動力學方程，因此利用該方程來研究力學系統(tǒng)的動力學具有極大的普遍性。因此，可以說，拉格朗日方程是力學中一個非常重要的理論工具。

［1］顧致平.理論力學［M］.中國電力出版社，2011.

［2］周衍柏.理論力學教程［M］.人民教育出版社，1979.

［3］肖士珣.理論力學簡明教程［M］.人民教育出版社，1979.