幾種常用的正項級數審斂法的比較
石會萍
(滄州師范學院 物電系,河北滄州 061001)
幾種常用的正項級數審斂法的比較
石會萍
(滄州師范學院 物電系,河北滄州 061001)
無窮級數是高等數學的重要組成部分,而正項級數又是級數理論中重要的組成部分,判別正項級數的斂散性更是數項級數的核心內容。正項級數的判斂方法雖然較多,但使用起來仍有一定的技巧。本文歸納總結了幾種常用的正項級數判斂法,比較了這些方法的不同點,總結了幾種方法各自的特點與適用范圍,便于學習者節約時間,提高效率。
正項級數 收斂 發散
無窮級數是高等數學的一個重要組成部分,它是表示函數、研究函數的性質以及進行數值計算的一種工具[1]。而數項級數又是無窮級數的一個重要組成部分,正項級數又是其中很重要的一類。因為許多數項級數都是通過將其化成正項級數而知其斂散性的,因此,正項級數的審斂就顯得尤為重要。正項級數有幾種審斂法,但一些學生學習中卻有些茫然,看到一個級數不知選擇哪種方法審斂,針對這種情況,現將幾種常用的正項級數的審斂法比較如下:
上面這兩個方法適用于一般項是n的有理式、無理式以及含有正弦函數、對數函數的正項級數。利用這兩個方法判定一個正項級數的斂散性時,都需要預先選定某個收斂(或發散)的級數作為比較級數常用的比較級數是-P級數和等比級數。
以上這兩種方法的優勢是不用另外找比較級數,只用該級數本身即可判斂,不足之處是當1=ρ時此法失效。
綜合以上,當需要判別一個正項級數的斂散性時,可按以下方法進行:

解 (1)本題適宜采用根植判別法。由于

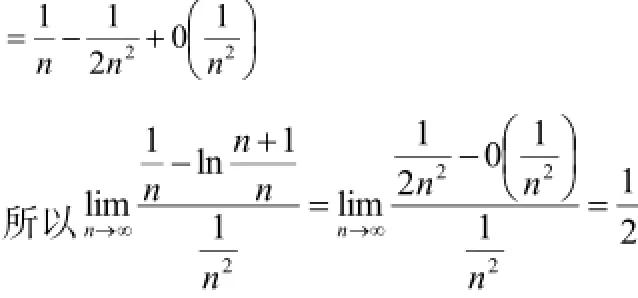
[1]同濟大學數學系.高等數學(第六版)[M].北京:高等教育出版社,2007.
[2]四川大學數學系高等數學教研室.高等數學(第三版)[M].北京:高等教育出版社,1996.
[3]王沖.淺析正項級數的比較判斂法[J].滄州師范學院學報,2015,3.

