多元組合ACS-TSP系統

陳 芳

（大同市安福儀器儀表有限責任公司，山西大同037003）

多元組合ACS-TSP系統

陳 芳

（大同市安福儀器儀表有限責任公司，山西大同037003）

文章提出了用多算法結合蟻族系統（ACS）求解旅行商問題（TSP）的方法，介紹了在ACS-TSP問題上的遺傳算法，目的是為了尋找處理旅行商早期停滯現象的解空間。此外，還提出了一種新的最小生成樹（MST）算法，結合最近鄰（NN）來創建一個初始架構，以便又快又好地解決旅行商問題。

ACS-TSP；遺傳算法；最小生成樹；最近鄰

螞蟻系統（AS）[1-2]也稱為蟻族系統（ACS）[3]，是由Dorigo和他的同事首先提出的，后來經過不斷地完善而發展起來的一種蟻群算法。蟻族系統已經被成功地應用于許多領域，如旅行商問題（TSP）[4]、二次分配問題[5]、數據挖掘[6]、空間規劃[7]、作業車間調度和其他方面[8-9]。

ACS-TSP算法與遺傳算法（GA）、模擬退火（SA）和進化規劃（EP）[10]等算法相比較能夠產生更好的效果，但仍然需要解決兩類問題，即早期停滯和收斂時間。早期停滯是一種現象，當信息素幾個弧的強度變的很高時，螞蟻將一次又一次地構建相應的路線，這就使得在選擇最優路徑時變得不可能。本文的目的是結合其他算法解決上述問題。

1 基于蟻族系統的TSP問題

蟻族系統是在螞蟻行為尤其是覓食行為的啟發下產生的，自然界中的螞蟻通過信息素來存放信息，以實現互相溝通。螞蟻的選擇傾向于以正相關的強度來發現線索的特定路徑。如果其他螞蟻沒有獲得更多的信息素，那么信息素就會消失，即信息失去強度。相反，如果許多螞蟻選擇某一路徑下的信息素，會使得路徑的信息強度增大，從而吸引越來越多的螞蟻。

應用ACS解決TSP的工作原理是：M螞蟻最初被隨機定位在n個城市，每只螞蟻根據轉移概率規則來選擇城市，從而制定完整的路線。在構建路線的同時，螞蟻通過應用本地更新規則來改變信息素的數量，當所有螞蟻構建完成了他們的路線時，全局性的更新將被應用。ACS算法框架為：

1.1 狀態轉換規則

k螞蟻的任務是構建一條訪問所有城市，然后回到起點的路線。與k相關的還有待參觀的城市Jk(r)，其中，r是螞蟻k目前所處的城市。螞蟻k從城市r到城市s所使用的規則稱為偽隨機比例選擇規則（或稱狀態轉換規則）：

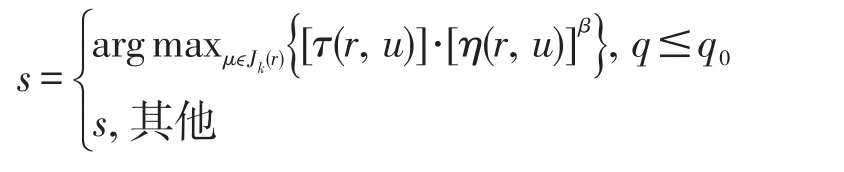
其中，τ(r,u)代表邊緣信息素的量；η(r,u)是城市r和城市u之間距離倒數的啟發式函數；β是用來衡量信息素路徑相對重要性的參數；q表示在區間[0,1]上隨機選擇的概率；q0是一個參數，0≤q0≤1；s是隨機變量，表明了螞蟻從城市r選擇去城市s的可能路徑。

s由下述方程給出：

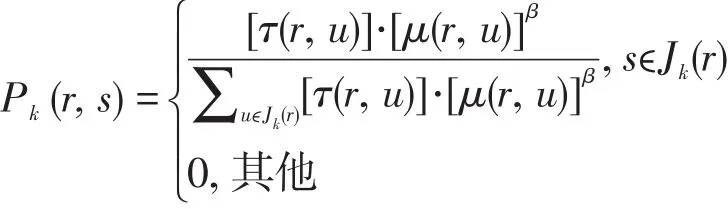
1.2 局部更新規則

構建一個解決TSP的方案，螞蟻通過應用下面的本地更新規則來訪問邊緣路徑和改變信息素路徑的數量：

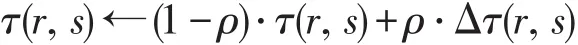
其中，ρ表示信息素衰減的參數，0＜ρ＜1；Δτ(r,s)代表初始信息素的水平，Δτ(r,s)＝(n*Lnn)-1；Lnn代表由最近鄰啟發式產生的路徑長度；n代表節點數。

1.3 全局更新規則

全局更新是在所有螞蟻已經完成了他們的路徑之后被執行的，信息素的數量是通過應用下面的全局更新規則來更新的：

其中，α代表信息素衰減參數，0＜α＜1；Lgb是最優路徑長度。

2 解決方案

本文運用遺傳算法來尋找解空間，以避免出現早期停滯現象，從而獲得解決TSP問題的全局最優解。此外，應用最小生成樹（MST）構建初始路徑來提高算法的效率。

2.1 遺傳算法

在每次循環中，通過讓最好的螞蟻去更新路徑來提高ACS的性能。但太早排除其他潛在的螞蟻會導致早期停滯現象，所以在解決ACS問題上引入遺傳算法來處理早期停滯現象。

遺傳算法（GA）[11]是一種基于遺傳和自然選擇原則的優化和搜索技術，由John Holland等人開發。遺傳算法是在基因概念的基礎上衍生出來的，其中包括三個重要的環節，即復制、交叉和變異。這些基因操作只使用原始操作，如復制、交換和翻轉基因。利用遺傳算法求解最優化問題的優點：（1）遺傳算法包括開發以及在操作過程中的探索，這與優化的方法（如梯度下降法）不同；（2）通過利用遺傳算法，不僅能夠解決線性與非線性規劃，還能解決整數規劃。

在全局更新階段，采用了兩相策略來提高尋找解空間的能力。在第一階段，當所有螞蟻完成了他們的路線后，在所有的螞蟻路徑中選擇三條有代表性的路徑：一是最優路徑，二是中等路徑，三是最劣路徑。對于這三條路徑，應用遺傳算法交叉算子的后代方法。在第二階段，應用最優路徑和GA所構建的三條其他路徑來解決全局邊緣信息素的更新問題。全局更新規則為：

利用上述方法，可以改進ACS-TSP算法框架為：

2.2 旅行商問題的構建方法

最近鄰（NN）方法通常是用來構建一個旅行商路線，但這樣的方法可能會產生嚴重的錯誤。最小生成樹（MST）的問題是找到一個最小總成本的生成樹圖，可以由krushal和Prim算法驗證，一個最優路徑通常包含70～80%的邊緣最小生成樹。

基于上述現象，采用一種新的與NN相結合的MST方法來構建一個初始路徑。根據具體的TSP問題，構建相應的MST樹，形成屬于MST樹的候選邊緣集。因為MST是一個n樹，其節點的自由度大于2，選擇最長的路徑，把從后代節點到祖先節點作為起始路線。然后，把初始路徑的結束點作為新的起始節點。選擇下一個節點方法為：（1）存在一個沒有被候選邊緣集訪問的邊緣，該邊緣連接新的起始節點。（2）如果上述方法不成功，則運用NN方法選擇最近的沒有被訪問的節點作為下一個節點。

在初始階段，利用上面提到的方法，增加少量的信息素以便螞蟻尋找路徑，從而減少收斂時間，最初的路徑構建程序框架如下：

3 實驗結果

為了驗證上述方法的合理性，在計算機上進行模擬。在實驗中設置如下參數：q0=0.9，ρ=0.5，α=1，β=2，計算機模擬運行=50。此外，在實驗中使用了20只螞蟻，與之前Dorigo提出的ACSTSP方法相比較，試驗結果表明：a280、att532、rat783、u1060、fl1400、rl1889是基準問題。圖1顯示的是ACS-TSP路徑長度和使用rl1889基準問題的對比情況。ACS+TSP+ls與Improved+ls計算路徑長度的對比結果，見表1。結果表明，利用TSP與遺傳算法以及最小生成樹相結合的方法，較好地解決了全局最優解或接近全局最優解的問題。

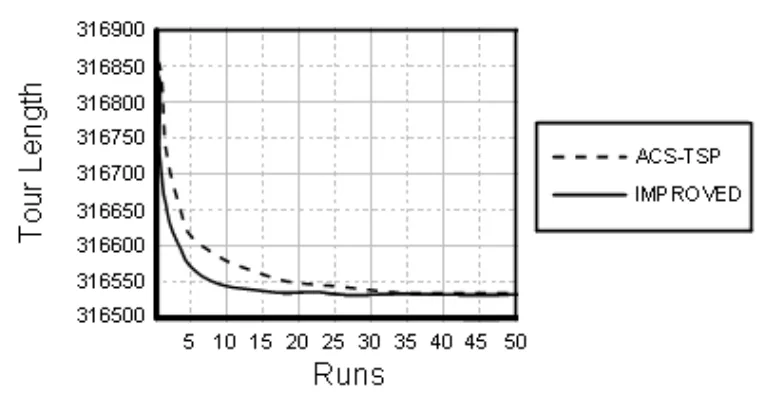
圖1 ACS-TSP路徑長度和使用rl1889基準問題的對比

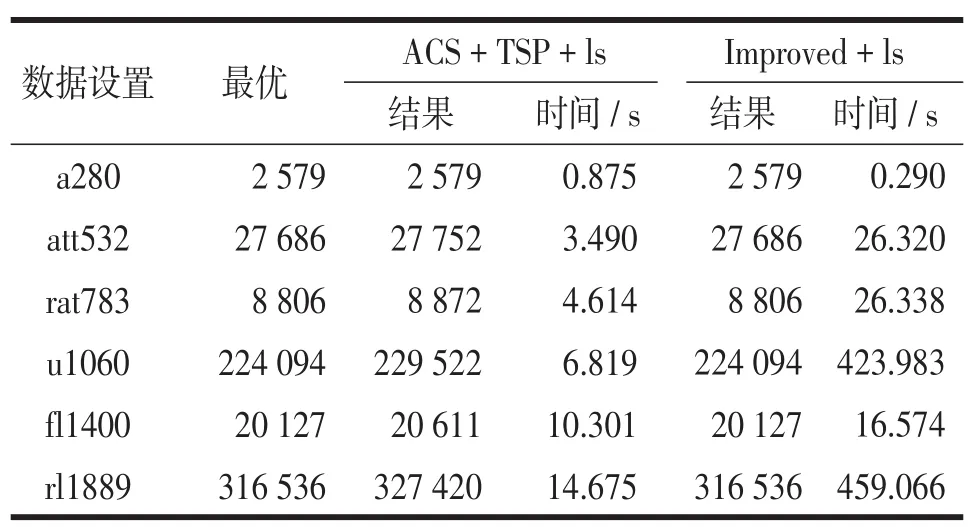
表1 ACS+TSP+ls與Improved+ls計算路徑長度的對比

4 結語

多元組合ACS-TSP系統是一種新的可以迅速提高初始路徑的戰略方法，對大型TSPs決策也能勝任。

[1]Colori A,Dorigo M,Maniezzo V.Distributed optimization by ant colonies[A].Varela F,Bourgine P.Proceedings of the first Europe an conference on artificial life[C].Paris:Elsevier Publishing,1991:134-142.

[2]Dorigo M,Maniezzo V,Colorni A.The ant system:optimization by a colony of cooperating agents[J].IEEE Transactions on Systems,Man,and Cybernetics-Part B,1996,26(1):29-41.

[3]Dorigo M,Gambardella L M.Ant colony system:a cooperative learning approach to the traveling salesman problem[J].IEEE Transactions on Evolutionary Computation,1997,l(1):53-66.

[4]Tsai Cheng-fa,Tsai Chun-wei,Tseng Ching-chang.A new Hybrid heuristic approach for solving large traveling salesman problem[J].Information Sciences,2004,166(1-4):67-81.

[5]Maniezzo V,Colorni A.The ant system applied to the quadratic assignment problem[J].IEEE Transactions on Knowledge and Data Engineering,1999,11(5):769-778.

[6]Parpinelli R S,Lopes H S,Freitas A A.Data mining with an ant colony optimization algorithm[J].IEEE Transactions on Evolutionary Computation,2002,6(4):321-328.

[7]Bland J A.Space-planning by ant colony optimization[J].International Journal of Computer Applications in Technology,1999,12(6):320-328.

[8]Blum Christian.Ant colony optimization:introduction and recent trends[J].Physics of Life Reviews,2005,2(4):353-373.

[9]Dorigo M,Caro G D,Gambardella L M.Ant algorithms for discrete optimization[J].Artificial Life,1999,5(2):137-172.

[10]Bonabeau E,Dorigo M,Theraulaz G.Swarm Intelligence:From Natural to Artificial Systems[M].New York:Oxford University Press,1999.

[11]Holland J.Adaptation in Natural and Artificial Systems[M].Ann Arbor:University of Michigan Press,1975.

A Multi-Metaheuristic Combined ACS-TSP System

CHEN Fang
（Datong Anfu Instrument and Meter Limited Liability Company,Datong Shanxi,037003)

This paper presents a Multi-Metaheuristic combined Ant Colony System(ACS)-Travelling Salesman Problem(TSP)al?gorithm for solving the TSP.We introduce genetic algorithm in ACS-TSP to search solutions space for dealing with the early stagnation problem of the traveling salesman problem.Moreover,we present a new strategy of Minimum Spanning Tree(MST)coupled with Nearest Neighbor(NN)to construct a initial tour for improving TSP thus obtaining good solutions quickly.According to our simulation results,the new algorithm can provide a significant improvement for obtaining a global optimum solution or a near global optimum solution in large TSPs.

ACS-TSP;genetic algorithm;minimum spanning tree;nearest neighbor

TP301

A

1674-0874(2015)05-0069-04

2015-09-20

陳芳（1991-），女，山西大同人，助理工程師，研究方向：企業信息化軟件開發與應用。

〔責任編輯 王東〕