基于非支配遺傳算法的自動化倉庫動態貨位優化*

印 美，洪榮晶，劉 林

（1.南京工業大學機械與動力工程學院，南京 211816；2.江蘇省工業裝備數字制造及控制技術重點實驗室，南京 210009）

基于非支配遺傳算法的自動化倉庫動態貨位優化*

印 美1，洪榮晶1，劉 林2

（1.南京工業大學機械與動力工程學院，南京 211816；2.江蘇省工業裝備數字制造及控制技術重點實驗室，南京 210009）

針對存有隨機數量貨物的機床零部件自動化立體倉庫（AS/RS）中存在的貨位規劃難題，提出了一種基于動態的倉儲模式與Pareto遺傳算法的AS/RS貨位優化方法。該方法以能耗最低和效率最高為基本原則規劃庫區和優化分配貨架，完成貨位編號和貨品編號；以堆垛機行駛時間和貨架穩定性為優化目標，建立貨位多目標優化的數學模型；采用第二代非支配排序遺傳算法得到動態貨位優化的Pareto最優解。仿真實例計算結果表明，該方法使貨物的出入庫能量消耗、出入庫效率以及貨架的穩定性等指標得到較大改善。

自動化立體倉庫；貨位動態分配；多目標優化；遺傳算法

0 引言

自動化立體倉庫（AS/RS，Automated Storage&Retrieval System）是指人工不直接進行處理的自動存儲和取出貨物的系統，它具有占地面積少、貨位處理速度快、準確率高、降低庫存積壓等優點［1］，對現代物流系統的作業效率和系統性能具有重要影響，在機床零部件的自動化管理系統中得到了廣泛應用。

貨位分配是影響自動化立體倉庫作業效率和系統性能的重要因素，為了進一步提升自動化立體倉庫性能，相關學者在自動化立體倉庫貨位分配優化方面進行了大量研究。羅鍵等［2］根據出入庫點到貨位小車的時間進行貨位分區并進行了貨位優化。楊鵬等［3］針對多載具自動化存取系統的貨位分配優化問題進行了研究。MoonG等［4］研究了存儲量變化時分類隨機存儲策略和貨物再次分類策略對存儲效率的影響，根據存儲量變化的大小選擇相應的貨物存儲策略。Ediz等［5］以貨位分配、貨位檢索和貨位存儲保持最小化為目的建立數學模型，并基于最優訂貨策略采用遺傳退火算法進行求解。

上述研究是在倉庫空倉情況下的靜態貨位優化，通常情況下倉庫存儲著一定量的貨物，同時存在出入庫，需要隨時給入庫貨物分配貨位。此外，考慮到節能環保，本文將降低能耗對存儲成本的影響作為優化目標之一。因此，綜合考慮貨位優化過程中能耗的影響、倉庫的運行效率和貨架的穩定性，建立多目標約束的優化模型，提出了一種基于第二代非支配排序遺傳算法的動態貨位優化分配方法，為出入庫貨物選擇最佳貨位。

1 自動化立體倉庫貨位問題描述

以某機電企業的立體倉庫為例，每一巷道有左右兩排貨架。假設立體倉庫每一列貨位數量一致，貨格大小相同，有n排p列q層，其貨位的長度、高度分別為l、h，并將最接近入庫臺的一排記為第一排，最接近巷道口的一列記為第1列，最底下一層記為第1層，位于第x排y列z層的貨位記為（x，y，z）（x=1，2，…，n；y=1，2，…，p；z=1，2，…，q）。針對上述倉庫布局模式，下面采用分類隨機存儲策略結合貨架受力均勻和穩定性原則、效率原則、分散存放原則進行自動化倉庫的動態貨位分配，具體分配策略內容如下：

（1）貨位編號。為了形成貨位的優先級順序，需要對倉庫貨位的單位能耗進行排序，文獻［6］中給出了一種貨位單位能耗因子d（h，L）

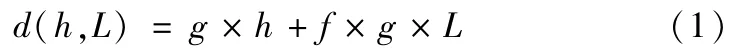
式中，g為重力加速度/m·s-2；h為貨格的高度/m；L為貨物所在貨位到出入庫臺的水平距離/m；f為軌道與輸送小車的摩擦系數。

根據公式（1），按d（h，L）由小到大的原則對倉庫的貨位進行排序并編號。貨位編號的大小對應于貨物存入該貨位時所消耗能量的大小，當立體倉庫的構造和布局確定時，可以得到相應的貨位單位質量的能耗值，排序后單排貨位編號如圖1所示。

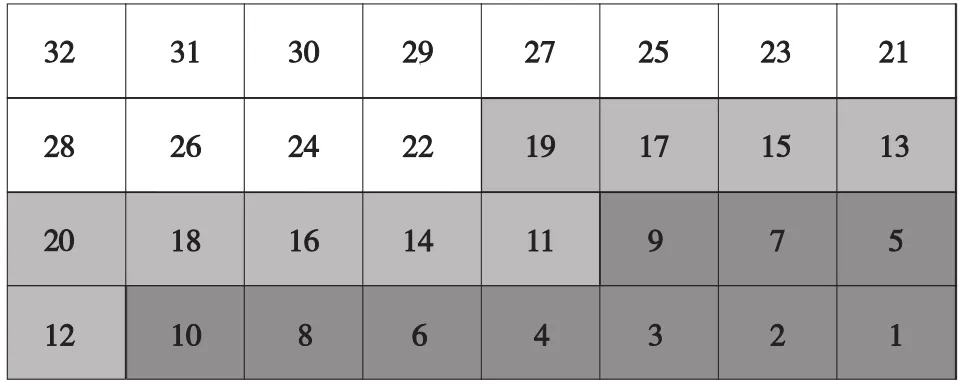
圖1 單排貨位編號

（2）貨位聯合編號。為了滿足相同貨品的分散存放和堆垛機運行的平衡，綜合各巷道貨架貨位進行統一編號。將每排貨架對應貨位從左到右進行順序編號，形成穿梭于各巷道之間的貨位鏈，如圖2所示是聯合編號完成后貨位排序。

圖2 聯合編號示意圖

（3）貨品編號。為了使每個貨品與合理的貨位形成一一映射關系，依據貨位-貨品耦合原理［7］，需要對貨品的立方體索引號值（Cube-per-Order，COI）進行計算。由Heskett［8］給出的立方體索引號規則，并考慮到能耗的影響，將貨品的COI值計算公式修改為：

式中，Ik表示某種貨物k的COI值；Ck表示貨物k存儲總量所需的庫存容量；fk表示貨物k的出庫頻率；mk表示貨物k的質量。

貨品鏈的形成根據公式（2），由貨品的COI值從小到大對貨品進行排序，其順序反映了貨品的出入庫頻率和質量，然后將COI值低的貨物與貨位編號小的貨位相對應，即將出入庫頻率高且質量大的貨物放置在距離出入口近并且單位能耗低的貨位上，這樣既能提高出入庫的效率又能降低倉庫的運行成本。

2 貨位優化多目標數學模型

根據貨架穩定性原則和效率原則，以倉庫運行能耗最低、出入庫時間最小化和重心最穩作為優化目標，以倉庫的實際運行狀況為約束條件，建立貨位優化的多目標數學模型。

2.1 貨位區優化

設有s種貨品，貨位分區的目的是讓貨品的COI值Ik（k=1，2，…，s）較小的貨品放置在單位能耗低的貨位上，即使Ik與貨位編號D的乘積Q最小，數學描述為：

2.2 出入庫時間分析

假設堆垛機在X方向、Y方向和Z方向均以勻速運動的，速度分別為vx、vy、vz，不考慮制動、啟動堆垛機的耗時及伸入貨格進行操作的時間，則出入庫效率優化的數學描述為：

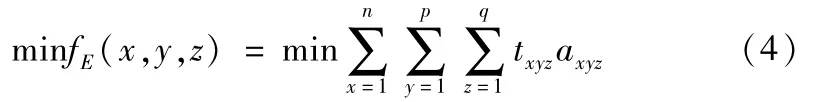
式中，txyz=（x+（x/2））d/vx+max（l×y/vy，h×（z-1）/vz），表示將貨物送到分配的貨位運行時間最小。axyz=0或1，為0時表示（x，y，z）貨格沒有貨物，為1時表示（x，y，z）貨格有貨物。

2.3 貨架穩定性分析

為了達到貨架穩定目標，即重心最穩，將貨物在貨架上的分布視作質點系，其數學描述為：

式中，Gz、Gy和Gxyz分別表示貨架的垂直重心、水平重心和貨架（x，y，z）貨位處的貨物重量，式（5）為了使貨架的垂直重心接近貨架的底層，使貨架穩定；式（6）是為了使貨架的水平重心接近貨架水平方向的中心軸線。

因此，貨架穩定性目標的數學描述為：

由于貨架水平穩定性和垂直穩定性同樣重要，貨架任何一邊不穩定都會造成嚴重后果，所以在水平和垂直方向上設置相同的系數，均為0.5。

2.4 貨位優化數學模型

綜上所述，貨位優化的多目標數學模型可以描述為：

貨架一共有n排p列q層，x、y、z均為正整數，分別表示貨架的排、列、層，且1＜x＜n，1＜y＜p，1＜z＜q。

3 基于遺傳算法的貨位優化設計

由上述分析，貨位動態分配優化模型是一個多目標優化問題，對于多目標優化問題，各個目標是相互沖突的，求解的關鍵是獲得由Pareto最優解組成的集合，用遺傳算法求解多目標問題的方法主要有SPEA2、NPGA2、SPGA、NSGA、NSGA-Ⅱ等，而第二代非支配排序遺傳算法（NSGA-Ⅱ）較其他算法具良好的穩定性、收斂性以及所求得的Pareto最優解集分布均勻［9-10］，本文采用該算法對貨位動態分配的多目標問題進行優化，并且在個體生成時進行約束處理，使其滿足約束條件，從而保證每個個體都是可行解。

基于NSGA-Ⅱ算法求解貨位分配優化模型的步驟：

（1）獲取當前的庫存狀態（包括貨品與貨位的信息）；

（2）輸入當前的任務信息（包括出入庫、貨品的任務數等）；

（3）初始化并編碼。設置最大迭代次數Kmax、種群數目pop、交叉概率pc、變異概率pm。采用實數編碼，初始化群體，并計算個體適應度值；

（4）將群體個體進行非支配分層，設置虛擬適應度，計算個體擁擠度算子，修改虛擬適應度，按照輪賽制選擇算子，進行選擇，形成新種群；

（5）執行交叉、變異操作，在此對產生的個體進行約束處理，避免非法產生非法個體；

（6）精英保留策略，將父代種群Pt與子代種群Qt合并為臨時種群Rt，進行非支配分層，并計算每個個體局部擁擠距離，依據輪賽制選取pop個個體，形成新的父代種群；

（7）在此基礎上進行選擇、交叉、變異，形成新的子代種群。如果迭代次數大于最大次數Kmax，則迭代終止；

（8）得到優化后的貨位坐標，進行模擬仿真驗證，根據優化結果，對貨位重新排序。

如圖3所示，為求解貨位分配優化的算法流程圖。

圖3 求解貨位分配優化的算法流程圖

4 應用實例

4.1 基本參數

某自動化立體倉庫有4排，每排8列4層，貨位的長度d=120cm，寬度l=120cm，貨位的高度h=80cm，堆垛機的水平運行速度vx=1 m/s、vy=1 m/s，垂直運行速度vz=0.5 m/s。貨物的參數如表1所示，第一列表示貨物1的質量是20 kg，作業概率為30%，需要的貨位個數是50個，分配在B區，以此類推，已知每類貨物的質量，作業概率和所需要的貨位數。

表1 倉庫貨物基本參數

根據貨位區分配結果，質量越大、作業效率越大的貨物放在距離出入口越近貨位區的可能性越大，即1類貨物放在B區，2類貨物放在C區，3類貨物放在A區，倉庫貨物基本參數見表1。

仿真計算實例中，假設共有2個貨物需要入庫，其中1類貨物、2類貨物各1個。共有2個貨物要出庫，為3類貨物。貨位進行優化前，倉庫的布局情況見圖6a，當前庫存為15個，分別是1類貨物5個，2類貨物4個，3類貨物6個。

4.2 仿真結果

仿真結果分析：按照上述NSGA-Ⅱ對多目標優化問題的求解方法，設置算法種群規模為200，交叉概率為0.9，變異概率為0.1，進化最大代數為100。編程并對其進行數值模擬計算，運行結果如圖4所示。

圖4 種群均值和解的追蹤曲線

圖5 目標函數解的分布

圖4 為種群均值和解追蹤曲線，圖5為目標函數解的分布圖，由圖4、圖5可見，種群進化到70代時已基本收斂，當種群進化到100代時，Pareto最優解具有良好的多樣性，NSGA-Ⅱ的搜索結果是令人滿意的。

選取其中的三組具有代表性的Pareto最優解作為貨位優化方案，對比貨位優化前后的三個目標函數值，如表2所示，較之優化前，其貨物存儲能耗fQ、出入庫時間fE和貨架重心fG平均值分別降低了39.20%、61.84%和47.62%，在Pareto最優解集中，三個目標之間是競爭關系，當其中一個減小時，必然會導致其他兩個目標值相應增大。

表2 優化前后三個目標函數值對比

4.3 模型驗證

如圖6所示，是采用數值模擬計算出的優化前后貨位分配狀態的三維示意圖。對比優化前后貨位分配狀態表明，優化前的貨位布局不合理，倉庫的綜合性能比較差，貨位優化后，貨位分配布局合理，滿足出入庫效率和貨架穩定性要求且能耗最低。同類貨物的貨區有相應的空缺貨位，是因為再次入庫時可以直接存放貨物到對應貨位區，無需再進行倒庫操作。再次出庫時，僅需取出相應貨位區的貨物即可。此外，由仿真結果知，并非所有Ik較小的貨物都放在編號較小的貨位上，這是因為貨位優化是一個多目標的問題，多個目標相互矛盾，在求解的過程中，為了滿足多目標最優，部分優化目標有妥協的趨勢。

圖6 優化前后貨位分配狀態對比

5 結論

本文提出了一種基于NSGA-Ⅱ算法的自動化立體倉庫動態貨位優化方法，該方法在綜合考慮堆垛機運行時間最短和貨架重心最穩的前提下，兼顧了倉庫運行能耗最低為優化目標，通過對生成個體進行了約束處理有效地避免非法個體的產生，較好地解決了貨位優化多目標之間相互沖突的妥協求解問題。仿真實例表明，所建立的模型能較好的兼顧貨位分配時的能耗、效率和貨架穩定性要求，得到的Pareto最優解為出入庫貨物分配了合理貨位，該優化算法可滿足工程應用實際需求。

［1］中國倉儲協會倉儲設施與技術應用委員會.自動化立體倉庫應用及發展展望［J］.物流技術與應用，2013（4）：106-108.

［2］羅鍵，鐘壽桂，吳長慶.基于離散粒子群算法的A VS/R S貨位優化［J］.廈門大學學報，2009，48（2）：212-215.

［3］楊朋，繆立新，戚銘堯.多載具自動化存取系統貨位分配優化［J］.計算機集成制造系統，2011，17（5）：1050-1055.

［4］Moon G，Kim GP.Effects of relocation to AS/RS storage location policy with production quantity varition［J］.Computer and Industrial Engineering，2001，l（4）：1-13.

［5］Atmaca Ediz，Ozturk Ayla.Defining order picking policy：A storage assignment model and a simulated annealing solution in AS/RS systems［J］.Applied Mathematical Modeling，2012，37（7）：5069-5079.

［6］銀光球，何福英，盛冬發.自動化立體倉庫中庫位優化模型研究［J］.福建工程學院學報，2006，4（3）：347-350.

［7］張蹺萍，劉文煌.CIMS物流系統的關鍵技術［J］.計算機集成制造系統，1997，3（1）：22-24.

［8］Heskett J L.Cube-per-order index-a key to warehouse stock location［J］.Transportation and Distribution Management，1963，3（4）：27-31.

［9］Zitzler E，Thiele L.Multi-objective evolutionary algorithms：a comparative case study and the strength Pareto approach［J］.Evolutionary Computation，IEEE Transactions on，1999，3（4）：257-271.

［10］Kalyanmoy Deb，Amrit Pratap，Sameer Agarwa.A fast and elitist multiobjective genetic algorithm：NSGA-II［J］.IEEE Transaction on Evolutionary Computation，2002，6（2）：182-197.

（編輯 李秀敏）

Optimization for Dynamic Location Assignment of AS/RS Based on Non-dominated Sorting Genetic Algorithm

YIN Mei1，HONG Rong-jing1，LIU Lin2
（1.School of Mechanical and Power Engineering，Nanjing Tech University，Nanjing 211816，China；2.Jiangsu Key Laboratory of Digital Manufacturing for Industrial Equipment and Control Technology，Nanjing210009，China）

To solve the slotting optimization of AS/RS，in which random spaces were occupied，an optimization method based on the dynamic storage strategy and non-dominated sorting genetic algorithm II（NSGA-II）was proposed.In this method，low energy consumption and high efficiency were taken into consideration for the section assignment and the locations and goods were numbered.Then，the optimization model was established for location assignment by defining the optimal objectives as the travel time of Storage/Retrieval machines and the stability of the whole warehouse.Finally，the optimal Pareto solution of dynamic location assignment was obtained using the NSGA-II.A numerical example demonstrated the feasibility of the proposed method，which not only reduced the energy and time consumption of storage and retrieval cycle，but also improved the stability of the whole warehouse.

automated storage/retrieval system；dynamic location assignment；multi-objectives optimization；non-dominated sorting genetic algorithm

TH246；TG65

A

1001-2265（2015）03-0031-04 DOI：10.13462/j.cnki.mmtamt.2015.03.009

2014-05-30；

2014-06-03

國家自然科學基金資助項目（51375222）

印美（1989—），女，江蘇泰興人，南京工業大學碩士研究生，研究方向為機械制造及其自動化，（E-mail）ymclara@sina.com。