基于ARX參數模型的某型抗荷調壓器系統辨識
經驗人:王 鵬 楊曉萍 曹煜國
基于ARX參數模型的某型抗荷調壓器系統辨識
經驗人:王 鵬 楊曉萍 曹煜國
本文對系統辨識基本原理進行了簡要介紹,利用Matlab系統辨識工具箱,完成了某型抗荷調壓器的系統辨識與ARX(擴展自回歸模型)參數模型建立,其預測結果具有較高準確性。此方法對于在試飛階段缺少被試產品技術資料情況下,了解掌握系統輸入輸出特性具有較好作用。
抗荷調壓器是飛機抗荷系統的主要組成部分。調壓器根據飛機過載大小,將來自環控系統的引氣調節至合適的壓力范圍內,以供給飛行員抗荷裝具使用,其作用是減輕過載對人體機能的不良影響,提高飛行員抗過載能力,從而最大程度地發揮飛機的機動性。
對于抗荷系統飛行試驗來說,課題人員往往由于種種客觀原因,不能獲得被試產品詳細技術資料,導致需要用較多飛行架次評估系統性能,嚴重時會影響到型號試飛進度。
筆者通過學習相關系統辨識資料,結合日常使用Matlab經驗,以某型抗荷調壓器為對象,采用ARX參數模型完成了系統辨識,建立的系統模型能夠以飛機過載作為輸入條件,預測抗荷調壓器輸出壓力,預測精度能夠滿足系統評估需要。
系統辨識原理及方法
系統辨識原理
基于試驗數據及試驗過程的系統建模過程,通常稱為“系統辨識”,其實質是從輸入輸出數據中提取被研究對象的數學模型,它是系統建模的一個十分重要的途徑。
隨著現代控制理論的迅速發展,過程控制及計算機技術的不斷進步,“系統辨識”已經成為在理論和方法上都有著鮮明特色的學科,廣泛而有效地應用于航空航天領域。
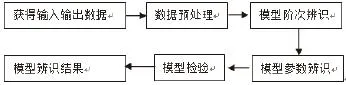
圖1 系統辨識流程圖
系統辨識的一般流程如圖1所示。
系統辨識方法
常用的系統辨識方法有:
非參數模型辨識方法
它是在假定系統是線性的條件下,不必事先確定模型的具體結構。主要有階躍響應法、脈沖響應法、頻率響應法、相關分析法、譜分析法等。
參數模型辨識方法
此方法必須假定一種模型,通過極小化模型與系統間的誤差準則來確定模型的參數。主要有最小二乘法、極大似然法、貝葉斯估計法、線性最小方差估計、神經網絡方法等。
其中最小二乘法因其結構簡單、收斂速度快、辨識精度較高、性能可靠、對先驗數據依賴低、且在工程上易于實現等眾多優點,因此受到工程人員和科研人員的重視,應用極為廣泛。
結合實際工作,本文選用參數模型辨識方法。
參數模型選取
就工程實際而言,一般化隨機模型為:
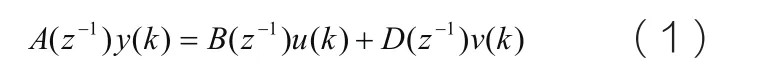
由此模型可提供以下模型:
(1) ARMAX模型(擴展自回歸滑動平均模型)
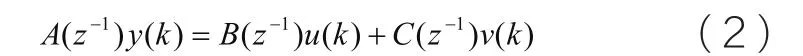
(2) ARX模型(擴展自回歸模型)
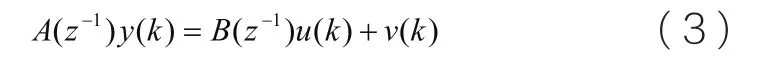
(3)Box-Jenkins模型(輸出誤差模型)
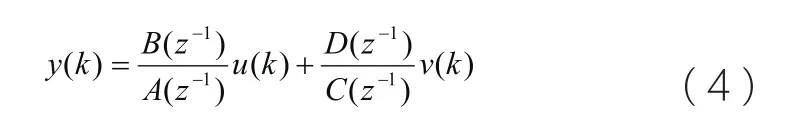
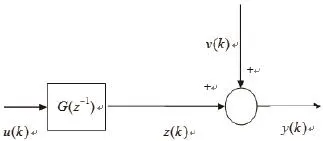
圖2 ARX模型結構示意圖
系統辨識時模型類的選擇要秉承最小化原理,盡量用最可能少的參數來表示要辨識的系統。因此,模型類的選用需要統籌考慮,兼顧多種因素。
本課題應用以上方法對實測數據進行辨識對比分析,其中ARX模型辨識結果擬合度較高。因此本文將重點說明某型抗荷調壓器ARX參數模型辨識的實現。
ARX模型結構如圖2所示。
圖中,輸入u(k)和輸出y(k)都是可以觀測的;G(z-1)是系統模型,用來描述系統的輸入出輸出特性;v(k)是白噪聲。
系統的描述方程為:
式中:y(k)為系統輸出量的第k 次觀測值,y(k-1)為系統輸出量的第(k-1)次觀測值,后面依次類推;u(k)為系統的第k 次輸入值,u(k-1)為系統的第(k-1)次輸入值,依此類推;將(5)式改寫為:
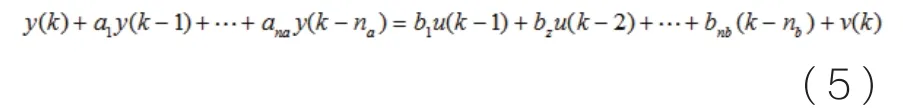
可得系統輸入輸出的最小二乘格式為:
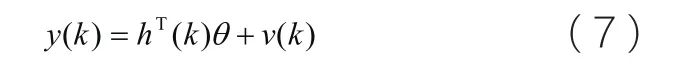
式中:h 為樣本集合;θ為被辨識的參數集合。
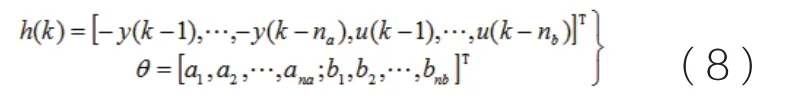
取準則函數

通過式(9)可以看出,未知模型參數θ最可能的值是在實際觀測值與計算值之累積誤差的平方和達到最小值處,所得到的這種模型輸出能夠最接近實際系統的輸出。使得J(θ)為最小值時θ估計值記作稱為參數θ的最小二乘估計值。求得的必要條件為:

某型抗荷調壓器ARX參數模型的Matlab實現
Matlab系統辨識工具箱包括了ARX模型、ARMAX模型、Box-Jenkins模型和狀態空間模型等。表1列舉了Matlab中常見的參數模型辨識函數。
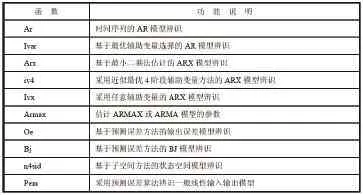
表1 參數模型辨識函數
輸入輸出數據獲取及預處理
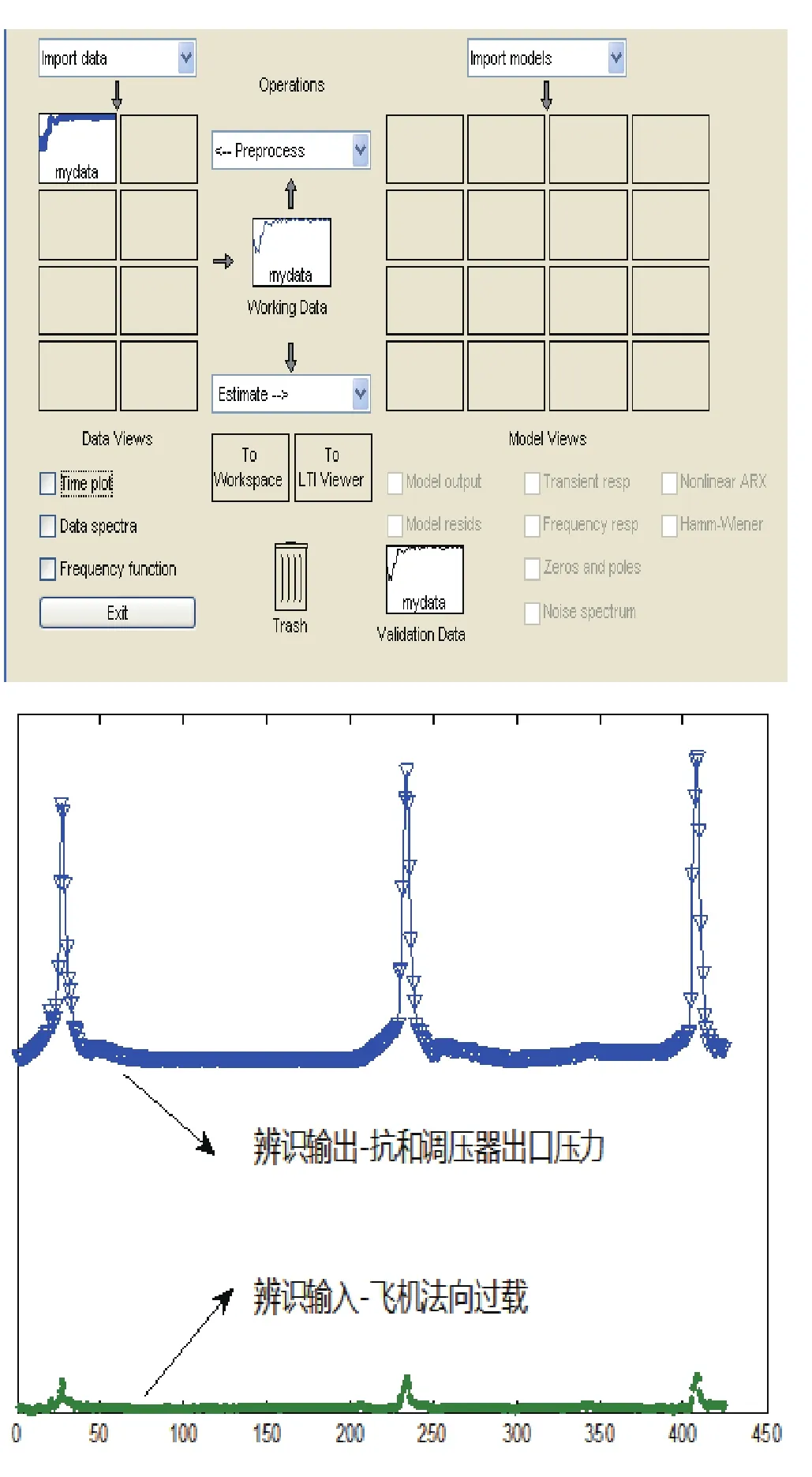
圖3 輸入輸出數據導入及預處理結果
對于某型抗荷調壓器來說,將飛機過載值作為輸入(x1),抗荷調壓器出口壓力作為輸出(y1),導入Workspace,用繪圖指令(plot)將數據畫成曲線, 觀察了解系統的時域或頻域特性。對輸入輸出數據要進行異常值剔除、數據有效性檢驗、數據類型和結構轉換等預處理。利用iddata命令生成標準包含輸入輸出數據的對象。如圖3所示。
模型定階
Matlab辨識工具箱已提供了方便、直觀的模型階次選擇工具。模型的辨識算法已封裝到ARX函數中。系統辨識工具箱可以生成以下多種類型的模型:頻率響應模型、沖擊響應模型、低階傳輸函數(過程模型) 、輸入輸出多項式模型、狀態空間方程模型、非線性(黑箱)模型、常微分或差分方程(灰箱)模型。
調用Matlab中計算多個單ARX模型損失函數的函數為arxstruc和模型結構選擇函數為selstruc,它可以計算和比較ARX模型的損失函數值,并得到最小損失函數所對應的階次(圖4中紅圈顯示)。
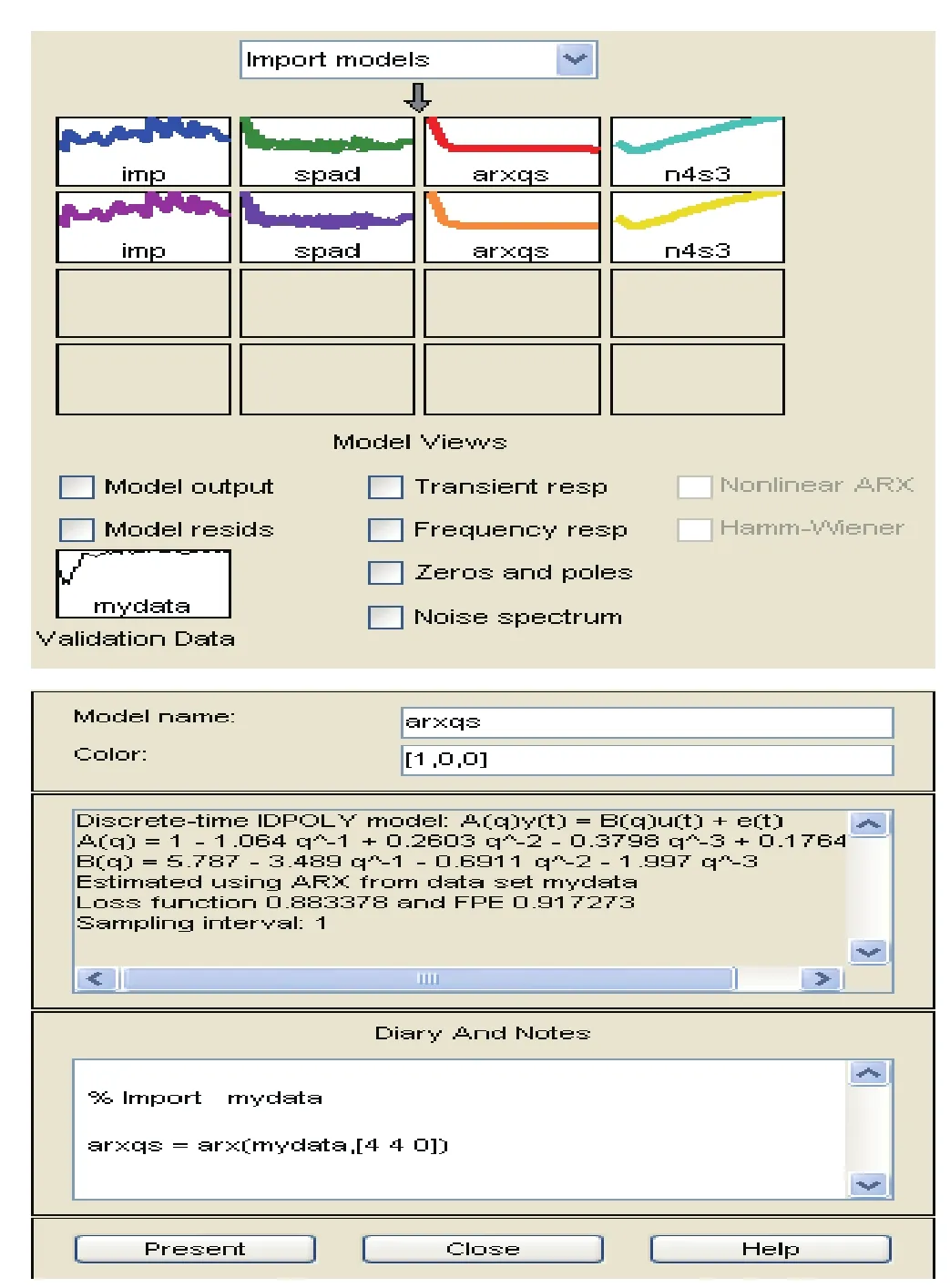
圖4 模型定階結果
傳遞函數獲取
通過上述模型定階可以得出系統離散模型的系數,調用Matlab中的d2c函數,可以將上文辨識得出的離散模型轉換為控制系統傳遞函數模型。
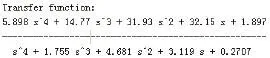
系統模型檢驗
將試驗數據中的輸入(飛機法向過載數據)作為辨識得到的ARX模型的輸入,獲得仿真輸出,與實測輸出(抗荷調壓器出口壓力)進行對比,計算擬合度。圖5是采用辨識得到的模型預測的抗荷調壓器出口壓力,可以看出模型擬合度較高,達到了89%(圖5中紅圈)。
圖6是殘差互相關性分析。結果顯示:殘差在合理的公差帶以內,即模型參數在置信區間內,模型有效。
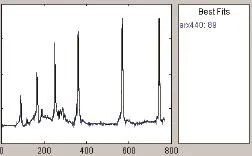
圖5 辨識模型預測數據與實測數據對比(擬合度89%)

圖6 殘差互相關分析
結束語
系統辨識方法在機理尚不清楚或機理過于復雜的系統動態特性研究中具有廣泛應用;
本文建立的某型抗荷調壓器ARX參數模型與文獻中抗荷調壓器模型在結構上具有一致性,從而驗證了系統辨識的準確性;
建立的系統模型能夠以飛機過載作為輸入條件,預測抗荷調壓器輸出壓力,預測精度能夠滿足系統評估需要,其結果具有代表性;
Matlab系統辨識工具箱具有強大的運算和分析功能,利用其進行系統辨識,可以大大提高辨識的速度和精度,并且辨識結果直觀,準確度高。
10.3969/j.issn.1001-8972.2015.10.043

