雙值約束三次規劃問題的全局最優性充分條件

葉 敏

(康居西城小學，重慶401331)

1 基礎知識

三次規劃問題有許多實際應用，比如金融、農業、組合證券投資選擇等方面［1－3］.吳至友［4－5］等人提出了一種研究全局最優性條件的新方法—L-次微分法來對一些特殊的非凸二次規劃問題的全局最優性充分條件進行研究，并得到了一些初步的研究成果.L-次微分與一般凸函數的次微分不同，一般凸函數的次微分是由一些線性函數組成的集合，而L-次微分可能是由一些非線性函數組成的集合.2010年，Wang等在文獻［6］中利用文獻［5］中所提出的抽象次微分為工具，建立了帶箱子或二元約束的三次規劃問題的全局最優性充分和必要條件;2012年，Zhang等在文獻［7］中研究了一些帶箱子或二元約束的一類特殊三次極小化問題的全局最優性充分條件.此處利用拉格朗日函數和L-次微分的方法，給出了雙值約束的三次極小化問題的全局最優性充分條件，而且得到了此類三次規劃問題在一些特殊情況下的結果，此結果與文獻［7］中的相應結論是一致的.同時給出例子說明給出的最優性條件能有效地用于確定給定的三次極小化問題的全局極小值，所得結果改進和推廣了文獻［7］中的相應結果.

考慮如下三次規劃問題:

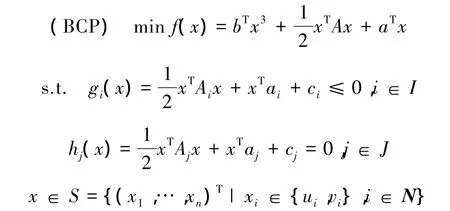
其中 ui，vi∈R，ui＜vi，i=1，2，…，n，b=(b1，…，bn)T∈Rn，a∈Rn，A∈Sn，Sn是所有 n×n 對稱矩陣的集合，).為了方便討論，不妨令 N={1，2，…，n}，I={1，2，…，m}，J={m+1，…，m+p}.

在文中，令L為一些特殊的三次函數組成的集合:

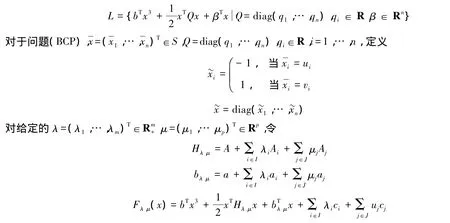
2 主要結果

在下面的證明中令L為如下二次函數組成的集合:

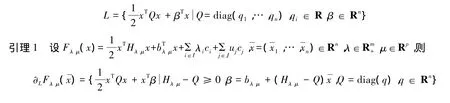
由引理1可以得到下面關于問題(BCP1)的全局最優性充分條件.

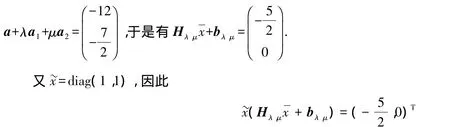
［1］HANOCH G，LEVY H.Efficient Portfolio with Quadratic and Cubic Utility［J］.JBus，1970(43):181-189

［2］LEVY H，Sarnat M.Investment and Portfolio Analysis［M］.New York:Wiley，1972

［3］HENIN C，DOUTRIAU J.A Specialization of the Convex Simplex Method to Cubie Programming［J］.Decis Econ Finance，1980(3):61-72

［4］WU Z Y，JEYAKUMAR V，RUBINOV A M.Sufficient Conditions for Global Optimality of Bivalent non-convex Quadratic Programs with Inequality Constraints［J］.JOptim Theory Appl，2007，133(1):123-130

［5］JEYAKUMAR V，RUBINOV A M，WU Z Y.Non-convex Quadratic Minimization Problems with Quadratic Constraints:Global Optimality Conditions［J］.Math Program A，2007，110(3):521–541

［6］WANGY J，LIANGZ A.Global Optimality Conditions for Cubic Minimization Problem with Box or Binary Constraints［J］.JGlob Optim，2010，47(4):583–595

［7］JEYAKUMAR V，LEE G M，SRISATKUNARAJAH S.Distinguishing a Global Minimizer from Local Minimizers of Quadratic Minimization with Mixed Variables［J］.Pac JOptim，2010(6):65-74

［8］LI G Q，WU Z Y.Global Optimality Conditions for Mixed Integer Quadratic Programming Problems［J］.Math Appl，2011，24(4):845-850

［9］ZHANG X M，WANG Y J，MA W M.Global Sufficient Optimality Conditions for a Special Cubic Minimization Problem［J］.Math Probl Eng，2012(2012):1-16

［10］ZHOU X G，CAO B Y.New Global Optimality Conditions for Cubic Minimization Subject to Box or Bivalent Constraints［J］.Pac JOptim，2012(8):631-647