基于ARIMA建模的重慶市第三產業(yè)產值預測*

徐 浩，劉宇琴

(1.重慶工商大學 電子商務及供應鏈系統(tǒng)重慶市重點實驗室，重慶400067;2.重慶工商大學管理學院，重慶400067)

隨著我國經濟社會的快速發(fā)展，第三產業(yè)對于經濟的發(fā)展越來越起到至關重要的核心作用.發(fā)達國家的GDP構成中，第三產業(yè)占到了GDP的80%左右，而我國第三產業(yè)占國民經濟的比重大約為40%.重慶在2013年的統(tǒng)計中，第三產業(yè)占本市生產總值的比重只有40.01%［1］，而天津、上海的第三產業(yè)占市生產總值的比重已經超過60%，北京更是達到了76%左右，大大超過重慶.《重慶十一五規(guī)劃》明確提出，要加快發(fā)展以服務業(yè)為核心的第三產業(yè)，把“促進服務業(yè)全面發(fā)展和升級擺在突出位置，充分發(fā)揮其促進經濟增長特別是促進就業(yè)的重要作用［2］”，因此研究第三產業(yè)產值的預測問題具有十分重要的意義。此處根據時間序列預測模型—ARIMA建立了重慶市的第三產業(yè)預測模型，并有十分優(yōu)異的擬合程度，為以后政府的決策提供了參考.

1 ARIMA模型簡介及建模

1.1 ARIMA 模型過程

ARIMA(autoregressive integrated moving average)模型簡稱自回歸求積移動平均模型，是1970年博克斯與詹金斯所提出.這種預測方法著重分析經濟時間序列本身的概率或隨機性質，而不在意構造單一方程或聯(lián)立方程模型，其主要優(yōu)點是對短期預測具有十分良好的效果［3］.張華初，林洪(2006)利用ARIMA模型對我國社會消費品零售額進行了預測，預測結果較好，并提出了擴大我國內需的建議［4］;池啟水(2007)利用ARIMA模型對我國的石油消費量進行了預測，結果表明，ARIMA模型很適合我國石油消費量的非平穩(wěn)時間序列的特點，擬合較好［5］;龔國勇(2008)也利用ARIMA模型對深圳的GDP進行了預測，結果表明，ARIMA模型可用于深圳國內生產總值短期預測，為深圳制定經濟發(fā)展目標提供決策參考［6］;蔣艷(2010)運用ARIMA模型預測了廣西固定資產投資，得出誤差在5%，可以接受［7］.此處選取ARIMA模型對第三產業(yè)產值進行短期預測，建模的主要過程包括:

1)自回歸過程(AR).若考慮時間序列 Yt－δ=α1(Yt－1－δ)+α2(Yt－2－δ)+…+αp(Yt－p－δ)+ut，其中，δ是 Y 的均值，ut是一個白噪聲，則表明Yt是一個p階自回歸，或AR(p)過程;

2)移動平均過程(MA).假定一個時間序列 Yt=μ+β0ut+β1ut－1+β2ut－2+…+βqut－q，其中，μ 是常數，u 和前面一樣，是隨機誤差項，則被稱為一個MA(q)過程;

3)自回歸移動平均過程(ARMA).當然，一個時間序列可能兼有AR和MA的特性，那么兼有的模型比如 Yt可以寫為 Yt=θ+α1Yt－1+β0ut+β1ut－1，其中有一個自回歸和移動平均項，所以就是 ARMA(1，1)過程.其中，θ為常數項;

4)自回歸求積移動平均過程(ARIMA).在一般的經濟時間序列中，原始的序列基本都不是平穩(wěn)的過程，假設一個時間序列經過一階差分后變?yōu)槠椒€(wěn)的時間序列，則這個時間序列Yt是一階單積的，即Yt～I(1).因此，如果必須將一個時間序列差分d次，將它變?yōu)槠椒€(wěn)的，然后用ARMA(p，q)作它的模型，則那個原始的時間序列是ARIMA(p，d，q)時間序列.p指回歸項數，d指變?yōu)槠椒€(wěn)的差分次數，q指移動平均次數.

1.2 ARIMA模型建立的一般方法

1)原時間序列的平穩(wěn)性檢驗，檢驗的方法一般是用單位根檢驗，若序列不滿足平穩(wěn)性條件，則可以通過差分來變平穩(wěn);

2)通過計算能夠描述序列特征的一些統(tǒng)計量，如自相關(ACF)系數和偏自相關(PACF)系數來確定ARMA(p，q)模型的階數p和q，并根據一定的準則如AIC等綜合考慮來確定模型的參數;

3)估計模型的未知參數，并通過參數的T統(tǒng)計量檢驗其顯著性，以及模型的合理性;

4)通過診斷分析，檢驗模型的擬合值和實際值的殘差序列是否為一個白噪聲序列.

2 重慶市第三產業(yè)產值序列ARIMA建模

2.1 數據的獲取及平穩(wěn)性處理

從重慶統(tǒng)計年鑒上統(tǒng)計出1978-2011年重慶市第三產業(yè)總值，見表1.

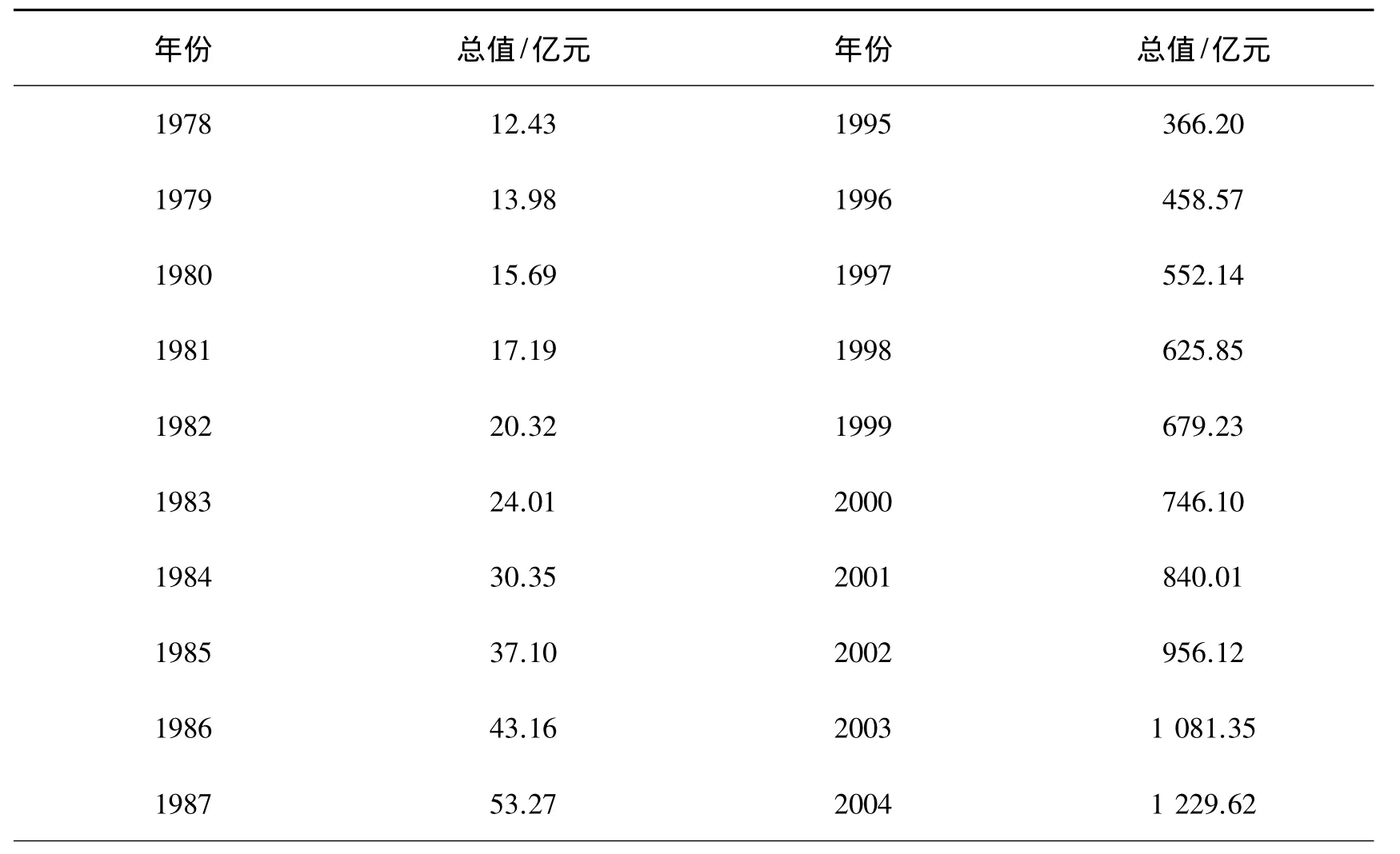
表1 1978-2011年重慶市第三產業(yè)總值

續(xù)表1

首先進行數據的平穩(wěn)性檢驗，使用Eviews 6.0作為檢驗軟件，如表2，對原始數據進行單位根檢驗.

表2 原始序列的ADF(單位根)檢驗

由表2可知，原始序列的τ統(tǒng)計量為0.923 626，遠遠大于在1%顯著性和5%顯著性以及10%顯著性下的臨界值，即接受H0∶δ=0的原假設，即存在單位根，所以原始時間序列是非平穩(wěn)的.

為了消除原序列的不平穩(wěn)，對原始序列取自然對數，實驗發(fā)現取一階差分后在1%，5%和10%顯著性下仍然不能通過ADF檢驗，即序列仍不是平穩(wěn)的，故取二階差分，記為Δ2ln Yt，再對取二階差分的序列進行ADF檢驗，可見時間序列趨勢基本消除，可以認為是一個平穩(wěn)的時間序列，如表3.

表3 二階差分后的ADF檢驗結果

表3中，經過二階差分后序列的τ值為－5.414 520，均通過1%顯著水平、5%顯著性水平以及10%顯著性水平的單位根檢驗，時間序列是平穩(wěn)的，即序列為二階單整序列，Δ2ln Yt～I(2).此模型中的d=2，即為二階單整的時間序列.

2.2 模型識別

模型識別的主要工具是自相關函數(autocorrelation function，ACF)和偏自相關函數(partial autocorrelation function，PACF)以及由此可得的相關圖(圖1).

由圖1的偏自相關函數(PACF)可以看出，p=1或p=2都可以，由自相關函數(ACF)圖可以看出，自相關圖 q=1 或 2 均可.利用最佳準則函數(AIC)可知，在 ARMA(1，1)，ARMA(1，2)，ARMA(2，1)和 ARMA(2，2)中，ARMA(1，2)的AIC和SC值最小，即赤池信息量和施瓦茨準則最小，故ARMA(1，2)為最優(yōu)的模型，如表4.

圖1 Δ2ln Yt的自相關及偏自相關圖

表4 4種模型的擬合估計結果比較

如表4，ARMA(1，2)的AIC值和SC值都最小，且R2在4個模型中最優(yōu)，所以選擇ARMA(1，2)模型作為估計模型，且差分次數為2，故最后的模型為ARIMA(1，2，2).2.3 ARIMA(1，2，2)模型的擬合和參數估計

建立 ARIMA(1，2，2)模型如下:

通過Eviews軟件的最小二乘法估計出方程的參數:

2.4 模型的診斷

圖2為殘差序列的前12階自相關圖(ACF)和偏自相關圖(PACF).

圖2 殘差序列的自相關圖和偏自相關圖

從圖2可以看出，自相關圖和偏自相關圖的相關函數均落在置信區(qū)間內，可以認為為白噪聲過程，同時，對殘差序列進行ADF檢驗.

表5 殘差序列的單位根檢驗

由上述檢驗可知，通過模型的擬合程度較好，可以進行下一步的分析.

2.5 模型的預測

由 ARIMA(1，22)模型:

最后預測的結果如表6.

表 6 ARIMA(1，2，2)模型預測值

通過模型預測，可以發(fā)現除了2011年的預測誤差百分比在－3.75%外，其余的誤差百分比都小于3%，預測的精度很好，預測精度在98%左右，表明了ARIMA(1，2，2)模型對于重慶市第三產業(yè)的產值具有良好的預測效果.

3 結束語

通過對1978-2011年重慶市第三產業(yè)產值序列進行分析，運用ARIMA(1，2，2)模型對第三產業(yè)的產值進行了預測，不僅預測結果的準確性較高，而且預測結果的穩(wěn)定性很好，可用為重慶市制定第三產業(yè)發(fā)展戰(zhàn)略規(guī)劃提供決策參考.在今后的研究中，可以將更多的預測技術作為方法，形成組合預測法，如ARIMA模型與灰色系統(tǒng)理論的結合，ARIMA模型與神經網絡的結合［5］，ARIMA模型與GARCH法結合等，運用更為先進和現代的預測方法對其進行預測.

［1］曾國平，劉娟.重慶第三產業(yè)發(fā)展水平差異分析［J］.商業(yè)研究，2009(11):4-7

［2］達摩達爾·古扎拉蒂.計量經濟學基礎［M］.北京:中國人民大學出版社，2009

［3］張華初，林洪.我國社會消費品零售額ARIMA預測模型［J］.統(tǒng)計研究，2006(7):58-60

［4］池啟水.中國石油消費量增長趨勢分析—基于ARIMA模型的預測與分析［J］.資源科學，2007，29(5):69-73

［5］龔國勇.ARIMA模型在深圳GDP預測中的應用［J］.數學的實踐與認識，2008，28(4):53-57

［6］蔣燕.ARIMA模型在廣西全社會固定資產投資預測中的應用［J］.數理統(tǒng)計管理，2006，25(5):588-592

［7］呂一清，何躍.基于灰色神經網絡的第三產業(yè)發(fā)展趨勢的預測模型［J］.統(tǒng)計與決策，2011(4):157-159

［8］劉勇，汪旭暉.ARIMA模型在我國能源消費預測中的應用［J］.經濟經緯，2007(5):11-13

［9］趙廷.ARMA在我國 GDP預測中的應用［J］.中國市場，2011(1):60-62

［10］張蔚，張彥琦.實踐序列資料ARIMA季節(jié)乘積模型及其應用［J］.第三軍醫(yī)大學學報，2002，24(8):955-957

［11］萬麗娟，徐孝勇.西部大都市區(qū)縣第三產業(yè)發(fā)展水平差異分析—以重慶市為例［J］.重慶大學學報:社會科學版，2010，22(16):6-10

［12］郎茂祥.預測理論與方法［M］.北京:清華大學出版社，2011