行列式的計算方法解析

楊關玲

(重慶師范大學數學學院，重慶401331)

當前，在教學領域中，無論是高等數學領域里的高深理論，還是現實生活里的實際問題，都或多或少地與行列式有著直接或間接的聯系.行列式的計算是一個重要的問題，也是一個很麻煩的問題.n級行列式一共有n!項，計算它有n!(n－1)個乘法.這是因為n級行列式的每一項都取自不同行不同列的n個元素的乘積，若把每一項都按a1j1a2j2…anjn排列，則對于a1j1a2j2…anjn有n!種排列，故n級行列式共有n!項.每一項都有n個數相乘，即每一項有n－1個乘法，共有n!(n－1)個乘法.二階行列式有2!項，三階行列式有3!項，當n較大時，n!是一個相當大的數字，直接從定義來計算行列式幾乎是不可能的事.因此，可以利用行列式的性質簡化行列式的計算.

行列式計算方法很多，而且一個行列式求解問題往往同時要用如上列舉出的一個或幾個方法才能解決.所以，在學習的過程中要學會觀察、探索，并有針對性總結.這里歸納介紹幾種具有典型特征的行列式解法.

1 關于n階行列式的計算方法［1-3］

1.1 直接利用定義計算(適用于行列式中有較多0的情況)

在引進行列式的定義之前，為了更加容易理解行列式的定義，首先介紹排列和逆序的概念.

(1)n級排列:由1，2，3，…，n組成的一個有序數組稱為一個n級排列.

(2)在一個排列中，如果一對數的前后位置與大小順序相反，即前面的數大于后面的數，那么它們就稱為一個逆序，一個排列中逆序的總數稱為這個排列的逆序數.

(3)逆序數為偶數的排列稱為偶排列，逆序數為奇數的排列稱為奇排列.

在做好這些工作之后，引入行列式的定義:

當行列式中的元素有較多的0，并且行列式的元素比較簡單時，不需要變形就可以直接利用行列式的定義計算出行列式的值.

1.2 利用行列式的性質，化為上(下)三角行列式計算

運用行列式的性質是計算行列式的一個重要途徑，大多數行列式的計算都依賴于行列式的性質，將行列式化成上三角(下三角或反三角)形式，再根據行列式的定義來計算行列式.

特征:第1行、列及主對角線外元素均為0(或可化為這種形式)的行列式(稱K型行列式)，可以化為上三角行列式進行計算.

1.3 利用行(列)展開定理進行降階，或作拉普拉斯展開

拉普拉斯定理 設在行列式D中任意取定了k(1≤k≤n－1)個行，由這k行元素所組成的一切k級子式與它們的代數余子式的乘積的和等于行列式D.

例2 在行列式

根據拉普拉斯定理

從這個例子來看，利用拉普拉斯定理來計算行列式一般是不方便的.這個定理主要是在理論方面應用.

1.4 利用遞推關系，或用數學歸納法證明

無論是初等數學，還是高等數學，遞推公式都有著非常廣泛的運用.適用遞推法計算行列式有以下規律:按照行列式的某一行(列)展開，會產生階數比原行列式低但卻與原行列式有著相同類型的新的行列式，運用遞推法逐層降階，最終將計算出原行列式的值.

例3 計算n階行列式

由式(1)(2)得 A=－2，B=3，所以 Dn=－2n+1+3n+1.

1.5 利用范德蒙行列式(或其他已知行列式)

對任意的n(n≥2)，n級范德蒙德行列式等于a1，a2，…，an這n個數的所有可能的差ai－aj(1≤j＜i≤n)的乘積，即ai－aj).值得注意的是范德蒙德行列式為零的充分必要條件是a1，a2，…，an這n個數中至少有兩個相等.

例4 計算行列式

1.6 加邊法

加邊法即在原行列式基礎上增加1行、1列(保持行列式值不變)，然后利用增加的行(列)對行列式化簡、計算.

解 通過加邊法把原來的n階行列式轉化為n+1階行列式進行計算

1.7 借助對應矩陣特征值的乘法計算

即 λi是 Ai的特征值，i=1，2，…，n.若 f(x)=a1+a2x+…+A 為 n 階矩陣，則 f(λ)=a1+a2λ+…+是f(A)=a1E+a2A+…+的特征值.

注:符合本題特征的行列式稱為循環行列式，因而如上結果具有一般性.此處用到方陣的特征值之積恰為其行列式的值，方陣的多項式的特征值恰是其特征值的多項式.

2 抽象型行列式的計算［4，5］

抽象型行列式一般不給出具體元素，它往往涉及與行列式相關聯的方陣、伴隨陣、逆矩陣、分塊矩陣，以及n維向量等的計算.因此，解決該類問題時應靈活運用矩陣的有關性質.，具體討論時應注意以下幾點:

(5)各行(列)以向量及其運算形式給出的行列式，可以按行(列)拆成幾個行列式之和;

(6)當已知矩陣的特征值時，可以用所有特征值之積計算.

例7 設A為n階方陣，且AA'=E(E是n階單位矩陣，A'是A的轉置矩陣)

1)對矩陣A+E右乘A'，再取行列式;

3 行列式按行(列)展開定理，及代數余子式的應用［6，7］

行列式按行(列)展開定理，以及一個行列式某一行(列)元素與另一行(列)對應元素的代數余子式乘積之和為零這兩個事實，在行列式代數余子式、方程組等的討論中有著廣泛的應用.如在求一個行列式某一行元素代數余子式之和時，逐個計算再求和，運算量很大，此時可借助行列式中改變某一元素的取值不影響該元素代數余子式的值這一特點，將該行元素都化為1，如此得到的行列式即如上要求的值.

(1)求 A31+A32+A33+A34.

(2)求 M12+M22+M32+M42.

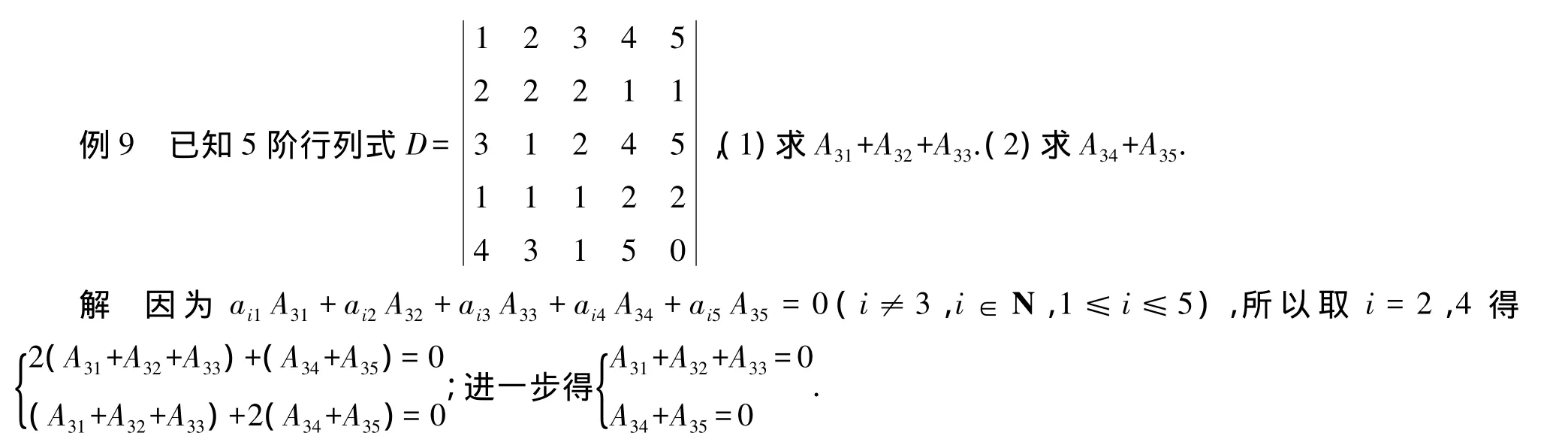
注:要求某一矩陣所有元素的代數余子式之和，可考慮先求其伴隨矩陣，再求伴隨矩陣各元素之和.

行列式的計算方法最常見的便是以上7種，但有時也因其結構不同而有其他類型的解法(如三對角線行列式的解法)，這里就不一一列舉了.在平時的學習中，有時還會碰見一些抽象型行列式的計算，行列式按行(列)展開定理，及代數余子式的應用.

以上計算行列式的基本方法奠定了高等數學的理論基礎，同時也為數學在現實生活中的廣泛運用提供了理論依據，總而言之，具有實質上研究價值.

［1］劉洪星.高等代數選講［M］.北京:機械工業出版社，2009

［2］徐仲，等編.高等代數［M］.3版.西安:西北工業大學出版社，2006

［3］王萼芳，石生明.高等代數［M］.3版.北京:高等教育出版社，2003

［4］陳東升，黃守佳.線性代數與空間解析幾何［M］.北京:機械工業出版社，2008

［5］劉先忠，楊明.線性代數［M］.3 版.北京:高等教育出版社，2008

［6］胡顯佑，彭勇行.線性代數習題集［M］.天津:南開大學出版社，2004

［7］吳世錦.四元數分量行列式的性質［J］.重慶工商大學學報:自然科版，2010，27(5):452-456