關于不定方程x(x+1)(x+2)(x+3)=Dy(y+1)(y+2)(y+3)(其中 D=21，23)

張 洪，羅 明

(西南大學數學統計學院，重慶400715)

設D是非完全平方數，對形如x(x+1)(x+2)(x+3)=21y(y+1)(y+2)(y+3)的不定方程已有不少研究工作［1－12］.此處將運用遞歸數列的方法證明當D=21和D=23時，不定方程

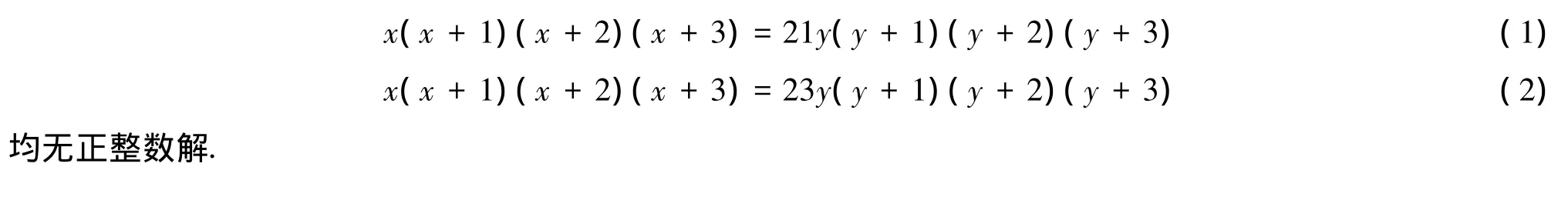
1 不定方程x(x+1)(x+2)(x+3)=21y(y+1)(y+2)(y+3)

先將方程(1)化為

易知方程X2－21Y2=－20的全部整數解［13］，由以下6個結合類給出:

顯然對?n∈Z有3|±y'n，由式(5)可以推出(2y+3)2≡2(mod 3)，此不可能，從而排除式(5).因此實際需要討論的只有式(4).

容易驗證下面各式成立:

下面將證明式(4)僅當n=0時成立，由此求得式(1)的全部正整數解.

1.1 (2y+3)2=－ 4yn+5解的證明

本節將考察式(4)的解，即n取何值時，－4yn+5是一個完全平方數.

引理1 只有n=0時，－4yn+5是一個完全平方數.

證明 由式(6)得yn＞1(n≠0)，從而－4yn+5是負數，不可能為一個平方數，當n=0時，－4yn+5=12，結果成立.證畢.

1.2 (2y+3)2=4yn+5 解的證明

引理3 若4yn+5是平方數，則必須n≡0(mod 100).

證明 用對序列{4yn+5}取模的方法證明.取 mod 29，排除 n≡1，2，4(mod 5)，此時 4yn+5≡12，17，3(mod 29)，剩余n≡0，3(mod 5).為節省篇幅，下面只給出每次取模所用的素數以及 n的剩余情況.取mod 421，剩余 n≡0(mod 5);取 mod 179，剩余 n≡0，5，10(mod 20);取 mod 149，199，剩余 n≡0(mod 25).綜合得剩余 n≡0，25，50(mod 100).對 n≡25(mod 100)，令 n≡100t1+25，若2|t1，則 n≡25(mod 40);若，則n≡5(mod 40).取 mod 41，排除 n≡25，5(mod 40)，剩余 n≡0，50(mod 100).對 n≡50(mod 100)，令 n≡100t2+50，若 2|t2，則 n≡10，50(mod 80);若，則 n≡30，70(mod 80).取 mod 239，排除 n≡10，50，30，70(mod 80)，剩余 n≡0(mod 100).

引理4 設n≡0(mod 100)，僅當n=0時4yn+5為平方數.

證明 令n=2·k·52·2t(t≥1，k≡1(mod 2))，對{5um±4vm}取mod 541所得的兩個剩余序列周期均為 45，而{2t}對mod 45的剩余序列具有周期12.對k分兩種情況討論.

1)k≡1(mod 4)時.當 t≡0，1，4(mod 12)時，令 m≡2t;當 t≡3，5，7，9，11(mod 12)時，令 m≡5·2t;當t≡2，6，8，10(mod 12)時，令 m≡52·2t.則當 t(≥1)(mod 12)=0，1，2，3，4，5，6，7，8，9，10，11 時，m(mod 45)=1，2，10，40，16，25，25，10，10，40，40，25，對應{5um+4vm}(mod 541)=323，360，479，356，357，247，247，479，479，356，356，247，這些數均為模 541 的平方非剩余.于是，由式(10)(11)及引理 2，得

從而4yn+5是非平方數.

2)k≡－1(mod 4)時.當 t≡2，3，6，9，11(mod 12)時，令 m≡2t;當 t≡0，4，8，10(mod 12)時，令 m≡5·2t;當 t≡1，5，7(mod 12)時，令 m≡52·2t.則當 t(≥1)(mod 12)=0，1，2，3，4，5，6，7，8，9，10，11 時，m(mod 45)=5，5，4，8，35，35，19，5，20，17，35，23，對應{5um－4vm}(mod 541)=356，356，331，447，479，479，455，356，247，250，479，428，這些數均為模 541 的平方非剩余.于是，由式(10)(11)及引理 2，有

從而4yn+5是非平方數.

2 不定方程x(x+1)(x+2)(x+3)=23y(y+1)(y+2)(y+3)

先將方程(2)化為

易知方程X2－23Y2=－22的全部整數解［13］，由以下兩個非結合類給出:

顯然必滿足 xn≥－1－1.從而式(13)(14)中的只需取

下面將證明式(13)僅當n=0時成立，式(14)僅當n=0時成立，由此求得(2)式的全部正整數解.

2.1 (2x+3)2=4xn+5 解的證明

本節將考察式(13)的解，即n取何值時4xn+5為完全平方數.

證明 當4|m 時，由式(17)知 um≡1(mod 4)，um≡1(mod 3)，um≡1(mod 23)，所以有－1≡1(mod 8)，92vm±5um≡±1(mod 4).由式(19)，可推知

引理6 若式(13)成立，則必須 n≡0(23×3×52×7).

證明 同引理3的證明類似，用對序列{4xn+5}取模的方法證明.由于數字23×3×52×7較大，證明分兩步進行.

1)取模 29，3109，2239，剩余 n≡0，18，28，46，54(mod 56).取模 7，47，13，167，1 511，4 871，剩余 n≡0，6，42，60(mod 84).綜合得剩余 n≡0，84(mod 168).對 n≡84(mod 168)，令 n≡168t1+84，若 2|t1，則 n≡4(mod 16)，取 mod 673，排除 n≡4(mod 16);若，則 n≡12(mod 16)，取 mod 31，排除 n≡12(mod 16).剩余n≡0(mod 168).

2)取模 2 351，11，2 819，101，2 099，44 201，剩余 n≡0，2，10，50(mod 100).取模 7，47，9 001，149，599，19 051，剩余 n≡0，21，60，75，90，120(mod 150).綜合得剩余 n≡0，150(mod 300).

綜上得 n≡0(23×3×52×7).

引理7 設 n≡0(23×3×52×7)，僅當 n=0時式(13)成立.

證明 令n=2·k·3·52·7·2t(t≥2，k≡1(mod 2))，對{5um±92vm}取mod 131所得的兩個剩余序列周期均為44，而{2t}對mod 44的剩余序列具有周期10.對k分兩種情況討論.

1)k≡1(mod 4)時.當 t≡1，3(mod 10)時，令 m≡2t;當 t≡7，9(mod 10)時，令 m≡5·2t;當 t≡5(mod 10)時，令m≡52·2t;當 t≡6，8(mod 10)時，令 m≡3·7·2t;當t≡2，4(mod 10)時，令m≡3·5·7·2t;當 t≡0(mod 10)時，令 m≡3·52·7·2t.則當 t(≥2)(mod 10)=0，1，2，3，4，5，6，7，8，9 時，m(mod 44)=8，24，24，8，8，8，24，24，8，8，對應{5um+92vm}(mod 131)=86，68，68，86，86，86，68，68，86，86，這些數均為模131的平方非剩余.于是，由式(20)(21)及引理5，得

從而4xn+5非平方數，故僅當n=0時(13)式成立.

2)k≡－1(mod 4)時.當 t≡6，8(mod 10)時，令 m≡2t;當 t≡2，4(mod 10)時，令 m≡5·2t;當 t≡0(mod 10)時，令 m≡52·2t;當 t≡1，3(mod 10)時，令 m≡3·7·2t;當 t≡7，9(mod 10)時，令 m≡3·5·7·2t;當 t≡5(mod 10)時，令 m≡3·52·7·2t.則當 t(≥2)(mod 10)=0，1，2，3，4，5，6，7，8，9 時，m(mod 44)=36，20，20，36，36，36，20，20，36，36，對應{5um－92vm}(mod 131)=86，68，68，86，86，86，68，68，86，86，這些數均為模131的平方非剩余.于是，由式(20)(21)及引理5，得

從而4xn+5非平方數，故僅當n=0時(13)式成立.

2.2 (2x+3)2=+5解的證明

引理8 若式(14)成立，則必須 n≡0(23×3×52×7).

1)取模 29，3 109，2 239，剩余 n≡0，28，30，52(mod 56).取模 7，47，13，167，1511，4871，剩余 n≡0，36，42，66(mod 84).綜合得剩余 n≡0，84(mod 168).對 n≡84(mod 168)，令 n≡168t1+84.若 2|t1，則 n≡4(mod 16)，取 mod 673，排除 n≡4(mod 16);若，則 n≡12(mod 16)，取 mod 31，排除 n≡12(mod 16).剩余 n≡0(mod 168).

2)取模 2 351，11，2 819，101，2 099，44 201，剩余 n≡0，40，50(mod 100).取模 7，47，9001，149，599，19051，剩余 n≡0，15，54，75，105，135(mod 150).綜合得剩余 n≡0，150(mod 300).

綜上得 n≡0(23×3×52×7).

引理9 設 n≡0(23×3×52×7)，僅當 n=0時(14)式成立.

證明 當n≡0(23×3×52×7)時，證明過程與引理7的一致，這里不再證明.

3 結 果

根據前面的討論，現給出文中的兩個主要結果.

定理1 不定方程x(x+1)(x+2)(x+3)=21y(y+1)(y+2)(y+3)無正整數解.

證明 由引理 1 有(2y+3)2=－4y0+5=1，因此 y=－1，－2.由引理 4 有(2y+3)2=4y0+5=9，因此 y=0，－3.由此，容易知道方程(1)僅有 16 組平凡解，即(0，0)，(0，－1)，(0，－2)，(0，－3)，(－1，0)，(－1，－1)，(－1，－2)，(－1，－3)，(－2，0)，(－2，－1)，(－2，－2)，(－2，－3)，(－3，0)，(－3，－1)，(－3，－2)，(－3，－3).因此不定方程x(x+1)(x+2)(x+3)=21y(y+1)(y+2)(y+3)無正整數解.

定理2 不定方程x(x+1)(x+2)(x+3)=23y(y+1)(y+2)(y+3)無正整數解.

證明 由引理7知，要式(13)成立，則必須n=0，此時x=0，－3.由引理9知，要式(14)成立，則必須n=0，此時 x=－1，－2.由此，容易知道方程(2)僅有 16 組平凡解，即(0，0)，(0，－1)，(0，－2)，(0，－3)，(－1，0)，(－1，－1)，(－1，－2)，(－1，－3)，(－2，0)，(－2，－1)，(－2，－2)，(－2，－3)，(－3，0)，(－3，－1)，(－3，－2)(－3，－3).因此不定方程x(x+1)(x+2)(x+3)=21y(y+1)(y+2)(y+3)無正整數解.

［1］COHN J E.The Diophantine Equation x(x+1)(x+2)(x+3)=2y(y+1)(y+2)(y+3)［J］.Pacific JMath，1971(37):240-331

［2］PONNUDURAI T.The Diophantine Equation x(x+1)(x+2)(x+3)=3y(y+1)·(y+2)(y+3)［J］.JLondon Math Soc，1975(10):232-240

［3］宣體佐.關于不定方程x(x+1)(x+2)(x+3)=5y(y+1)(y+2)(y+3)［J］.北京師范大學學報:自然科學版，1982(2):27-34

［4］羅明.關于不定方程x(x+1)(x+2)(x+3)=7y(y+1)(y+2)(y+3)［J］.重慶師范學院學報:自然科學版，1991，8(1):1-8

［5］徐學文.關于不定方程p2kx(x+1)(x+2)(x+3)=y(y+1)(y+2)(y+3)［J］.華中師范大學學報:自然科學版，1997(3):257-259

［6］LUO M.On The Diophantine Equation x(x+1)(x+2)(x+3)=6y(y+1)(y+2)·(y+3)［J］.Indian Jpure appl Math，2001(1):3-7

［7］程遙，馬玉林.關于不定方程x(x+1)(x+2)(x+3)=11y(y+1)(y+2)(y+3)［J］.重慶師范大學學報:自然科學版，2007，24(1):27-30

［8］段輝明，楊春德.關于不定方程x(x+1)(x+2)(x+3)=19y(y+1)(y+2)(y+3)［J］.四川師范大學學報:自然科學版，2009，32(1):60-63

［9］羅明，朱德輝，馬芙蓉.關于不定方程3x(x+1)(x+2)(x+3)=5y(y+1)(y+2)·(y+3)［J］.重慶師范大學學報:自然科學版，2009，26(5):16-21

［10］瞿云云，曹慧，羅永貴，等.關于不定方程x(x+1)(x+2)(x+3)=15y(y+1)·(y+2)(y+3)［J］.西南師范大學學報:自然科學版，2012，37(6):9-14

［11］郭鳳明，肖冬雪，安瑩.關于不定方程x(x+1)(x+2)(x+3)=10y(y+1)(y+2)(y+3)［J］.西南師范大學學報:自然科學版，2013，38(10):13-16

［12］郭鳳明，羅明.關于不定方程x(x+1)(x+2)(x+3)=13y(y+1)(y+2)(y+3)［J］.重慶師范大學學報:自然科學版，2013，30(5):101-105

［13］柯召，孫琦.談談不定方程［M］.上海:哈爾濱工業大學出版社，1980