屬性值為三角模糊數(shù)的多屬性群決策方法探究

□ 王本梅 周愛蓮 安吉縣道路運(yùn)輸管理局

屬性值為三角模糊數(shù)的多屬性群決策方法探究

□ 王本梅 周愛蓮 安吉縣道路運(yùn)輸管理局

［導(dǎo)讀］ 針對屬性值均為三角模糊數(shù)的多屬性群決策問題，提出了一種新的方法。該方法通過定義三角模糊數(shù)向量的內(nèi)積，計算專家評判的相似度和差異度，從而確定群體專家的權(quán)重。利用離差最大化得到屬性的權(quán)重，確定方案的群體綜合屬性值，利用模糊數(shù)大小的可能度得到排序權(quán)向量，從而給出方案排序結(jié)果。應(yīng)用實(shí)例驗(yàn)證了方法的可行性和合理性。

隨著學(xué)術(shù)界對決策問題的關(guān)注，相關(guān)研究也越來越多。大多數(shù)文獻(xiàn)都針對決策方法進(jìn)行研究，而對群體專家權(quán)重確定的問題很少涉及，一般都是假定專家權(quán)重相同或事先給定，太過于絕對化、經(jīng)驗(yàn)化。為此，本文針對屬性為三角模糊數(shù)的問題，重點(diǎn)研究專家權(quán)重和屬性權(quán)重的確定方法，通過定義三角模糊數(shù)向量的內(nèi)積，計算專家評判的相似度和差異度，從而確定群體專家的權(quán)重。通過離差最大化得到屬性的權(quán)重，確定方案的群體綜合屬性值，利用模糊數(shù)大小的可能度得到排序權(quán)向量。

1.三角模糊數(shù)相關(guān)定義

定義1［1］稱為三角模糊數(shù)，其隸屬度函數(shù)為即：

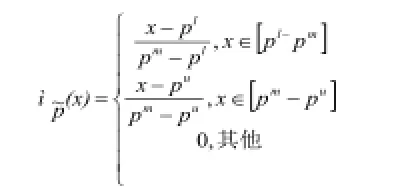
定義2［2］考慮任意兩個三角模糊數(shù)，根據(jù)擴(kuò)展原理，有相應(yīng)的模糊數(shù)運(yùn)算規(guī)則如下：

定義3［3］設(shè)為任意兩個三角模糊數(shù)，則稱的積。特別地，當(dāng)時，為的模。

定義6［3］設(shè)和為任意兩個正模糊數(shù)，稱：

定義7［4］設(shè)為任意兩個三角模糊數(shù)，則的可能度為：

定義8［4］設(shè)由n+1個三角模糊數(shù)構(gòu)成的集合為，則的可能度為：

2.群決策模型描述

本文計算出一位專家對于不同方案的不同權(quán)重，一個屬性對于不同方案的不同權(quán)重，更加細(xì)致、合理地刻畫了不同專家、不同屬性對決策結(jié)果的影響，更加符合實(shí)際。在考慮模糊多指標(biāo)決策問題中，由于各指標(biāo)的量綱可能不同，所以需要對原始決策矩陣進(jìn)行規(guī)范化，在此，假設(shè)屬性類型為效益型，利用文［1］將決策矩陣規(guī)范化為其中，

3.群專家權(quán)重的確定

一個專家的評判與群體評判的綜合結(jié)果越相近，則說明其可信度越高，其權(quán)重也應(yīng)越大。為求專家的權(quán)重，首先把專家的評價值按一定的方法形成一個多維向量，然后從兩個方面考慮：一是用兩向量的空間位置關(guān)系反映評判的總體相似性；二是用兩三角模糊數(shù)的距離反應(yīng)評判結(jié)果之間的差異性。

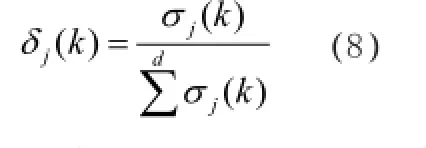
定義9［5］決策者對于方案的權(quán)重的定義為：

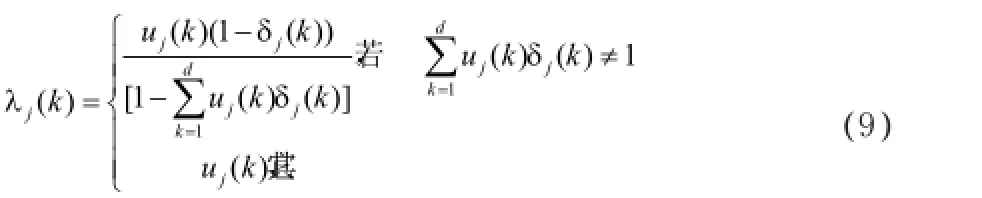
4.算例

表2 專家群體給出方案s1的屬性值

表3 專家群體給出方案s2的屬性值

表4 專家群體給出方案s3的屬性值

首先，規(guī)范化決策矩陣，由公式（7）、（8）計算各專家評價方案的相似度和差異度為：

由式（9）得到各專家關(guān)于方案的權(quán)重分別為：

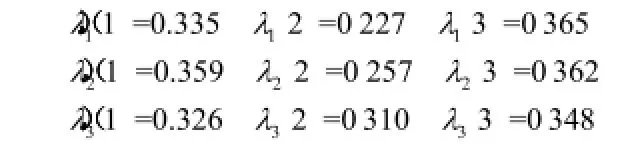
對決策者，由公式（10）求解各屬性的權(quán)重分別為：

由公式（11）得到各決策者對各供應(yīng)商的綜合屬性值，再由公式（12）得到各供應(yīng)商的群體綜合屬性值分別為：

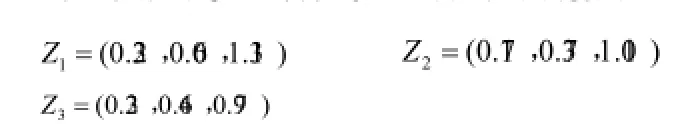
由于方案的群體綜合屬性值仍為模糊數(shù)，根據(jù)定義7、定義8計算方案大小的可能度，從而得到排序權(quán)向量［7］，其中，的值越大，對應(yīng)的方案越優(yōu)。計算結(jié)果如下：。所以最佳供應(yīng)商是s2。

5.結(jié)語

通過對模糊型多屬性群決策問題的研究，得出結(jié)論：（1）通過計算模糊數(shù)向量的內(nèi)積和距離得到其相似度和差異度，進(jìn)而得到專家權(quán)重，避免了主觀確定專家權(quán)重的不足，為模糊型多屬性群決策問題專家權(quán)重的確定提供理論依據(jù)。（2）在屬性權(quán)重完全未知的情況下，運(yùn)用離差最大化的方法建立非線性規(guī)劃模型，并求解該模型得到屬性權(quán)重，避免了主觀隨意性，使結(jié)果更加客觀可信。（3）將專家權(quán)重、屬性權(quán)重與決策矩陣進(jìn)行集結(jié)得到各供應(yīng)商的群體綜合屬性值。并利用方案大小的可能度得到排序權(quán)向量，從而確定方案的優(yōu)劣，避免了三角模糊數(shù)之間的直接比較。為權(quán)重未知的模糊型多屬性群決策問題提供一定的參考。

［1］張利萍，鄭彥玲.一種基于三角模糊數(shù)的模糊型多屬性群決策方法［J］.數(shù)理醫(yī)藥學(xué)雜志，2011，24（1）：15-18.

［2］周宏安劉三陽.基于離差最大化模型的模糊多屬性決策投影［J］.系統(tǒng)工程與電子技術(shù)，2007，29（5）：741-744.

∶

［1］王本梅（1985-），女，碩士研究生，主要研究方向?yàn)槲锪飨到y(tǒng)規(guī)劃設(shè)計。

［2］周愛蓮（1972-），女，副教授，碩導(dǎo)，主要研究方向?yàn)槲锪飨到y(tǒng)規(guī)劃設(shè)計。