平頭式塔機起重臂預翹度的設計研究
李 斌,李宏乾
(沈陽建筑大學 交通與機械工程學院,遼寧 沈陽 110168)
平頭式塔機起重臂預翹度的設計研究
李 斌,李宏乾
(沈陽建筑大學 交通與機械工程學院,遼寧 沈陽 110168)
針對平頭式塔式起重機起重臂在工作中產生的下撓問題,研究起重臂預翹度確定的理論和方法。通過研究起重臂在自重載荷和起重載荷的共同作用下,起重臂的下撓曲線和下撓量的計算分析方法,給出了起重臂撓曲線和下撓量的計算表達式。依據最大下撓量最小的原則確定了起重臂預翹度的設計方法和計算表達式,為平頭式塔式起重機的起重臂預翹度的設計奠定理論基礎。
平頭式塔式起重機;下撓曲線;設計方法;預翹度
平頭式塔式起重機在起重作業時,塔機起重臂在自重載荷和起重載荷共同作用下會出現不同程度的下撓。過大的下撓會減少塔機的實際起升高度,并使載重小車由大幅度向小幅度變幅過程中出現爬坡現象。
為解決這一問題,塔機設計者在設計時都使起重臂各節臂架的上弦桿長度略小于下弦桿的長度,以實現起重臂具有一定的預翹量,來抵消起重臂的下撓。但是這種設計還僅僅是基于經驗的基礎上,并沒有理論依據。為解決這一問題,本文運用結構在載荷作用下的彈性變形理論,研究起重臂在自重載荷和起重載荷共同作用下所產生的變形曲線和各節臂架端部的轉角和位移計算方法。并以相對水平軸線最大下撓量最小為原則確定了起重臂預翹度設置的理論和方法。以實現起重臂在合理的預翹度下使起重小車的最大爬坡度最小。這對減少起重小車的驅動功率,提高整機造型的和諧程度具有實際意義。
1 起重臂位移狀態分析
1.1 單節臂架受力與位移的關系
對于平頭式塔機起重臂,可將其力學模型簡化為懸臂梁。當起重臂受自重載荷和起重載荷共同作用時,可將其受力情況轉化為懸臂梁受均布自重載荷和集中起重載荷作用。設起重臂由n節臂架組成,選取任意一節臂架i(i=1,2,……,n)作為研究對象,分析其受力狀態。第 節臂架的受力情況如圖1所示,起重載荷作用于點A。均布自重載荷為qi,集中起重載荷為PQ,臂架長度為li。

圖1 第i節臂受力情況
參照圖1中的臂架受力情況可知,Pi為第i+1節臂架至第n節臂架的自重之和,Mi為分別將各節臂架的自重轉移到第i節臂架的端部B處,相應產生的附加力矩之和,起重載荷PQ與臂架根部的距離為x(x∈[0,li]),梁的剛度為EI,則起重載荷作用點A處的垂直位移和轉角位移分別為

式中的Pi和Mi取值如下


參照圖1中的臂架受力情況,當起重載荷作用于A點時,求得第i節臂架的端部B處的垂直位移和轉角位移分別為

起重載荷可以作用在任意一節起重臂臂架上的任意位置,端部集中載荷Pi和Mi以及起重載荷PQ都會有所不同,但載荷作用點和臂端位移計算方法不變。
上述的第i節臂架作用有起重載荷,第k節(k=1,2,…,≠i,i+1,i+2…,n)上沒有作用起重載荷,第k節只有自重載荷和端部載荷作用,其端部載荷確定方法如下。
1)當k>1時,

其中:j=k+1,k+2…,n-1;n為起重臂的節數。
2)當k<i時,

則第k節端部的位移計算表達式如下

1.2 起重臂整體位移分析
前面分析了各節起重臂的位移狀態,整個起重臂是由多節臂架組成的,并且處于根部的各節臂架位移都對處于端部的各節臂架的位姿有直接影響。以起重臂的前三節臂架AB、BC和CD為例(如圖2所示),分析各節臂架在總體坐標下的垂直位移和轉角位移。

圖2 起重臂變形曲線
參照圖2中的起重臂變形曲線可知,第一節臂架AB端部相對于臂根部有垂直位移Δ1,轉角位移θ1;第二節臂架BC端部相對第一節臂架AB有垂直位移Δ2,轉角位移θ2,則BC端部相對于起重臂臂根的垂直位移和轉角位移分別為

根據變形曲線可知:Δh1=Δ1,y1=l2sinθ1,Δ2′=Δ2cosθ1
代入上式得兩項位移如下

第三節臂架CD自身產生的垂直位移為Δ3,轉角位移為θ3,則第三節臂架端部相對于起重臂臂根的垂直位移和轉角位移分別為
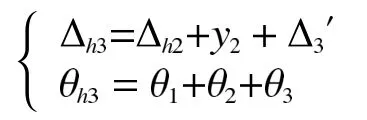
根據變形曲線可知

代入上式得兩項位移如下

由此可得任意第k節臂架端部相對起重臂臂根的兩項位移均可以描述為

其中:k=1,2…,n。
起重載荷作用在第x節起重臂的點x處,則點相對臂根的兩項位移可以描述為

其中:i=1,2…,n。
式(4)可以用來描述起重臂任意節端部的位移狀態,而式(5)可以用來描述起重載荷在任意一點處的位移狀態。
2 起重臂預翹度的研究
選取合理的預翹度既有利于塔機的整體造型,也有利于降低變幅降低驅動時的能耗。依據塔式起重機的起重特性,在超出額定最大起重量工作幅度后,不同的幅度具有不同的額定起重量。實際上塔機在日常工作時,任意幅度狀態下施加的載荷是很難確定的,起重特性給定的只是額定載荷,在任意幅度施加任意載荷,起重臂各節都會產生與之相對應的位移,也就是垂直位移和轉角位移,這些位移和轉角均可以依據式(1)、(2)和(3)進行計算。
為了減少起重臂的下撓量,在起重臂設計時使其具有一定的上翹量,對下撓量進行一定程度的抵消。起重臂是桿系桁架結構,由于加工上的原因起重臂的上翹都是采用折線上翹的形式,即使起重臂在連接點處上翹一定的角度。其處理的方法就是使上弦桿的長度短于下弦桿,兩節臂在連接點處就形成了一定角度的上翹。其上翹的角度可用如下方法分析計算。
設第k節起重臂末端上下弦桿長度差為δk,第k+1節與第k的連接處的上弦桿與下弦桿的長度差一般情況下也是δk,兩者連接銷軸間的距離為hk,得角度關系如圖3所示。

圖3 角度關系
參照如圖3可得在連接處產生的預翹角θqk

式(6)中關鍵的問題是如何確定起重臂末端上下弦桿長度差δk。如果δk確定了,則θqk就可以確定下來。
影響小車變幅阻力的實際上是起重載荷作用點的轉角位移,而影響起重臂外觀形態的是垂直位移變形,當然控制住了臂節端部的轉角位移也可以控制起重臂的垂直位移量。盡管作用在起重臂上的載荷具有隨意性,但塔機的起重特性曲線卻規定了不同幅度狀態下的額定起重載荷,不同幅度下的額定載荷也屬于塔機正常狀態下的極限載荷,這種載荷狀態可以形成起重臂的最大位移值。依據式(4)和式(5)可以計算出各節臂端部的位移值和載荷作用點的位移值。依據起重特性曲線對起重臂進行全幅度加載,可以得出全部 節起重臂端部的極限位移值變化域,也就是極限垂直位移變化域和極限轉角位移變化域,也就是由式(4)所計算結果的集合。還可以依據起重特性加載,得到沿全幅度變化的極限垂直位移變化值曲線和極限轉角位移曲線,也就是式(5)沿全程所得最大值。
對于一般的平頭式塔式起重機,起重臂的位移有兩個因素產生,一是起重載荷使起重臂產生位移;二是自重載荷使起重臂產生位移。一般情況下起重載荷作用在第i節起重臂,考核第節起重臂臂端的位移。則第k節起重臂端部位移的兩組參數域可以分別描述為[Δkmin, Δkmax]k≤i,[θkmin,θkmax]k≤i,其中,Δkmin和θkmin應該是k=i,且載荷作用點x=li時的取值,而Δkmax和θkmax應該出現在k與i差值最大的狀態。即最大幅度的額定載荷在各節臂端產生的位移是最大位移,而載荷作用在本節臂臂端時產生的位移是最小位移。自重載荷在各節臂端產生的位移Δkq和θkq是恒值。
一般狀態下Δkmax和θkmax都很難出現,可在介于兩組參數域中,取一個當量常數值,并將其作為第k節起重臂的常態最大值,即
起重臂的預翹度要保證起重臂在工作狀態和非工作狀態下最大垂直位移量最小,但從垂直位移進行考核起重臂的預翹度難以控制,而臂端轉角位移量實際上是與臂端垂直位移相對應的,而且小車運行阻力中包括爬坡阻力,取第k臂和第k+1節臂結合處形成的轉角上翹的角θqk為
依據式(6)可得

δk分別為第k臂和第k+1節臂架接合處的上弦桿與下弦桿的長度差,也就是在這個接合處,兩節臂架兩側的上弦桿比下弦桿分別短δk。
3 算例分析
現以PTT80(6010)型平頭式塔式起重機起重臂為計算實例,研究起重臂的預翹度。起重臂整體為一個變截面結構,共由七節臂架組成,最大幅度為60m。
依據起重特性表可知,二倍率時平頭塔式起重機在起重臂的最大幅度60m處起吊額定起重量1t時,在各節臂端部產生的轉角位移為最大位移;而分別在各節臂的端部起吊相對應的額定起重量時,產生的轉角位移為最小位移。
PTT80(6010)型平頭式塔式起重機的吊鉤重為1 920N,起重小車重為2 280N,二倍率起升鋼絲繩重為700N,起重臂的臂頭重為655N,臂頭長度為0.289m,則各節臂架參數見表1。
依據表1中各節臂架的參數,結合二倍率起重特性表與式(1)、(2)和(3)即可求得當起重載荷作用時,各節臂端產生的最大轉角位移θkmax和最小轉角位移θkmin及當自重載荷作用時,各節臂端產生的θkq的值,將結果列于表2。
依據表2中所求得的數據,結合式(8)和(9)即可求得PTT80(6010)型平頭式塔式起重機起重臂的各節臂架一側的上下弦桿長度差值,并將結果列于表3。

表1 臂架參數

表2 各節臂架轉角

表3 上下弦桿一側長度差
4 結 論
本文研究了平頭式塔式起重機起重臂位移的計算方法,給出了在任意起重載荷作用下起重臂各節臂架端部的位移計算表達式和載荷作用點的位移計算表達式,分析了各節臂架端部的位移變化值域,確定了各節臂架接合處預翹角度的確定方法,并依據預翹角度給出了臂架接合處兩側上下弦桿應有的長度差。
[1]李廉錕.結構力學第5版[M].北京:高等教育出版社,2011.
[2]袁尉卿,程海濤,趙 林.平頭塔式起重機起重臂上翹量值探討[J].建設機械技術與管理,2014,(3):87-89.
[3]鄭奠一,楊 陽.塔機水平起重臂空載時上翹高度的確定[J].建筑機械,1994,(1):11-14.
[4]鄒力生,王端秀.塔機小車起重臂端的預置起翹高度[J].建筑機械化,1988,(10):20-22.
(編輯 賈澤輝)
Research of hoist boom precast warpage design of the fl at type tower crane
LI Bin, LI Hong-qian
TH212;TH213.3
B
1001-1366(2015)08-0035-04
2015-05-09

