基于Agent的協同物流利潤分配模型

田 冉，韓 敏，李斌勇

（西南交通大學信息科學與技術學院，成都610031）

基于Agent的協同物流利潤分配模型

田 冉，韓 敏，李斌勇

（西南交通大學信息科學與技術學院，成都610031）

傳統Rubinstein利潤分配模型中的參數設定多由經驗判定，造成協商結果的不確定性。針對該問題，建立一種自學習的利潤分配模型。該模型將協同物流商分為主動協同和被動協同2類，不同類型的協同物流商在探索對方物流商底價的基礎上給出自己的報價或者反報價，依據當前報價結果決定是否轉變協商角色類型，并引入自學習的報價參數實現報價過程中報價策略的改變，得到使協同各方滿意的結果。仿真結果表明，與傳統Rubinstein利潤分配模型相比，該模型能降低達成協商所需的次數，有效避免因經驗判定造成的不確定性。

交通運輸經濟；利潤分配；報價策略；協同物流；討價還價策略

1 概述

協同物流運輸模式是現代物流運輸的發展方向和趨勢所在，而在協同過程中必然會產生由“1+1＞2”的協同效應所帶來的新的協同利潤，而如何分配新利潤就成為對物流鏈的協同的關鍵問題。由于協作企業之間是不同的利益主體，因此既要保證各方的利益，又要保證協同的整體利益最大化，在考慮協同各方利益的基礎上公平合理地分配協同物流運輸中產生的協同利潤，協調協同各方的關系，這是關系到協同物流能否順利進行和持續進行的基本問題。

目前，對于利潤分配的對象上可以分為橫向和縱向的利潤分配，對于物流鏈縱向利潤分配的主體主要為參與物流鏈上協同的物流商之間的利潤分配。對于物流鏈橫向利潤分配的主體主要為物流鏈多個層級上的物流商與制造廠、經銷商、供應商之間的利潤分配。

利潤分配方法主要集中在利潤的直接分配和利潤的協商分配（即討價還價）上，直接分配多采用Shaply值法及其改進方法［1-3］，協商分配多基于Stackelberg［4-6］，Bertrand［6-7］等博弈策略的基礎上建立K-S［4］，Rubinstein［8］等分配模型及與其他算法的混合算法［9-11］組成的分配模型。從經濟學研究的角度來說，現有的合作博弈理論是解決價格博弈問題的最佳策略，但是還存在一些問題，如在利潤直接分配上多采用的Shaply值法的結果優劣主要取決于利潤分配因素及其權重的定義。在利潤協商分配的過程中多采用合作博弈策略模型，如Stackelberg策略可以找到一個合作區間，但無法給出一個準確的利潤分配方案［12］。而Rubinstein討價還價策略雖然可以給出一個分配方案，但其設定參數對其還價策略的影響很大，當設定參數取值不合適時會陷入難以協商成功的困境。

隨著物流協同的不斷發展和物流鏈上企業間系統的相互集成，使用Agent根據環境的變化進行協商策略的變更，從而進行協同利潤的分配是一種很好的解決方案［13-15］。本文為各協作物流商建立擁有獨立報價的Agent，通過各Agent之間的相互學習探索對方的價格底線，從而改變自己的協同角色和修正自己的報價參數進行討價還價，最終實現各方都滿意的協作利潤分配。

2 協商模型

2.1 模型描述

對在協同物流的過程中產生新的利潤進行分配時，以協調Agent為主導，在主動協商物流商和被動協商物流商之間執行Stackelberg博弈策略。博弈的順序為主動物流商提出報價，使自己的利益最大，隨后由被動物流商根據主動物流商的報價再提出反報價，并使自己的收益最大。具體的流程如下：協調Agent首先在歷史數據中查詢是否有先例可以遵循，如果有則將其作為初始的利潤分配，由協調Agent直接廣播給各協同Agent。如果沒有則向分配利潤Agent發送分配請求，利潤分配Agent初始按照各物流商在協同中的貢獻度進行分配利潤，這里采用文獻［2］方法確定初始利潤分配方案，并將分配結果告知各協同Agent，如各協同Agent均同意該分配方案則結束協商，如不同意則進入多Agent協商過程。物流商Agent根據利潤分配Agent分配的價格（即第一次根據貢獻自動分配的報價）提出自己的反報價，并根據其他協作方的反報價探索其私有信息（例如底價和報價策略），并修正自己對于對方現有報價看法的主觀判斷，從而在兼顧協同的同時修正自己的報價策略和反報價，從而盡可能地提高自己所獲得的利益。

如各物流商Agent直接拒絕該方案則協商需要人為干預后再次協商。當協商次數到達最大協商次數后仍然沒有達成協議則協商結束。協商的過程如圖1所示。

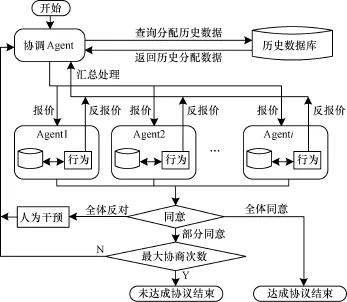
圖1 協商過程

這里將Agent分為協調Agent和物流商Agent，協調Agent負責利潤分配歷史數據的查詢、初始的利潤分配廣播和到達最大協商次數節點時人為干預協調終止的工作。

物流商Agent負責每個獨立的物流商在利潤分配過程中對報價的反應和對其他物流商底價的探索。其部分信息是私有的，即自身的底價和對報價的滿意度，而部分信息是公開的，即各個物流商歷史報價信息、反報價信息。

2.2 模型定義

多Agent的協商過程與協商次數、雙方底價、互相報價、各自的報價策略等因素有關。根據協同物流中利潤分配的實際情況，本文將協商模型定義為一個多元組（ST，SA，ACTION，T，RP，OP，β（t））：

（1）ST為進行協商的子任務，SA為進行協商的子任務的集合，即由運輸任務SA可以拆分出多個為運輸任務SA拆分的子任務個數。

（2）ACTION為該智能體的動作集合：接受（Accept），拒絕（Reject），報價與反報價（Offer and C_offer）。智能體按照當前的報價和規則進行行動。

（3）T為協商次數，定義Tmax為協商的最大次數，即協商不可能無休止地進行下去，當協商次數超過協商的最大次數時，停止協商。最大協商次數定義為：

其中，μ為事先定義的合理的協商次數；f（SA）為運輸任務SA分配協同的物流商數量；N為常數，用于控制協商的最大次數不至于過多。最大協商次數與參與協同的物流商數量成正比，當參與協同的物流商數量越多，參與協同的資源就越多，重新協商達成協同的機會就越大，協商的最大次數就越多，反之亦然。

（4）RP為該物流商的底價，對于該物流商來說如果報價低于底價則停止協商。參與協同的各個物流商是無法知道其他物流商的底價。只有通過不斷報價與反報價，最終達成協商。

（5）OP為物流商的報價與反報價的價格。物流商通過反報價來探索其他物流商的底價和報價參數，從而使得自己的利益最大化。同時定義OPe為最后的成交價格。

（6）β（t）為報價參數，與協商中的智能體的風險趨向和協商的次數相關。主動協商的報價參數定義為：

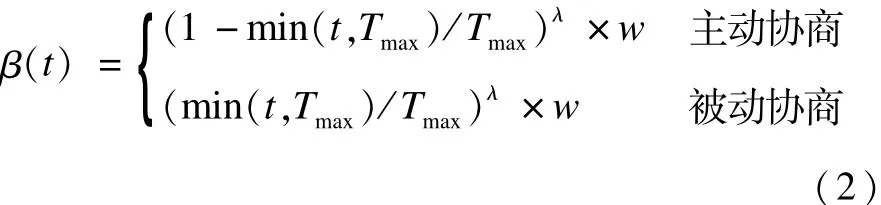
其中，β（0）=w；λ為正實數，決定了報價參數的變化速度；w∈（0，1］，決定了β（t）的最大值。當w=1時，圖2分別表示了λ=0.1，λ=1.0和λ=10.0在w=1.0時主動協商的β（t）的變化情況。

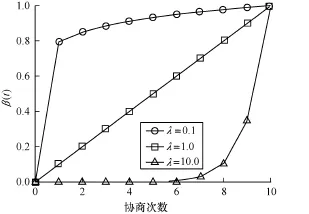
圖2 主動協商企業報價參數β（t）的變化過程

圖3分別表示了λ=0.1，λ=1.0和λ=10.0在w=1時被動協商的β（t）的變化情況。

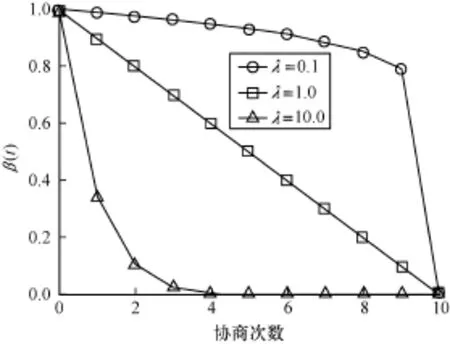
圖3 被動協商企業報價參數β（t）的變化過程

（7）物流商Agent對利潤分配報價的反應一般是模糊的，特別是對分配給自己的利益總希望更多一些。因此，對分配給自己的利潤價格可以建立模糊評價集合，即該物流商對報價的反應集合，對應的滿意度定義為：

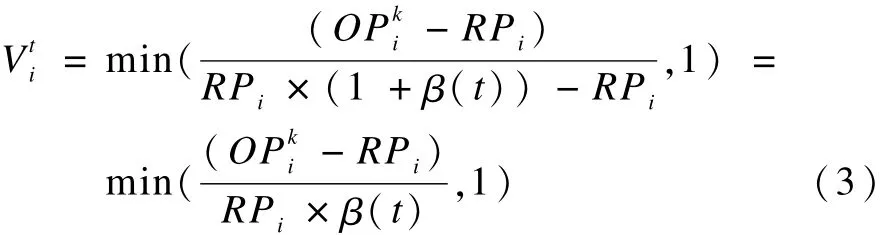
當物流商i對t時刻分配結果不滿意時，即滿意度小于1時，需要主動和其他協同物流商進行協商，即采用式（2）中的主動協商報價參數定義進行報價；當物流商i對t時刻分配結果滿意時，其滿意度在所有物流商中最大，即其在協商過程中僅需要被動接受其他物流商的協商要求，即采用式（2）中的被動協商的報價參數定義進行報價。

2.3 自學習協商算法

物流商Agent在觀察學習其他協同物流商反報價的基礎上判斷其他物流商對報價的反應類型，并提出自己報價分配方案與其他物流商進行協商。其學習的過程如下：

SteP1 查詢歷史

查詢分配歷史記錄判斷利潤分配Agent提出的報價方案是否在之前有過成功的先例。如果有則按此歷史方案進行廣播，如果所有Agent不反對則直接接受，結束協商過程。如果沒有則進入Step2。

SteP2 主動物流商的報價

假設需要對2個物流商a，b協作時產生的利潤S進行分配，此時對于物流商a來說，如果對初始報價方案不滿，即其滿意度此時物流商a需要主動和物流商b進行協商，因此，物流商a的Agent需要向總的協調Agent提出新的報價方案

對于物流商a來說，物流商b的底價RP′b是未知的，但其滿意度肯定大于自己，因此，需要給出一個對自己有利的報價方案。這里物流商a的協同Agent將物流商b的底價假設為一個可能值的集合｛B1，B2，…，Bq｝，每一個可能值的取值定義為：

假設從物流商b的反報價估算的物流商b的底價集合是滿足正態分布的，因此，歸一化后將其定義為：

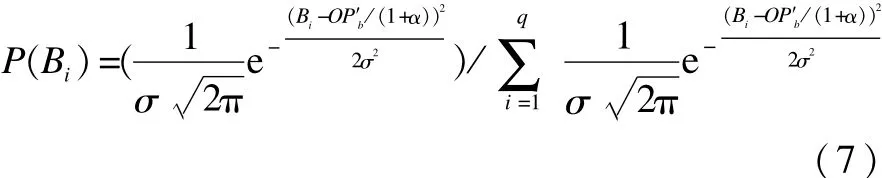
其中，σ2為底價變化的步長，當物流商b急于達成協商時，該值較小，反之則較大，因此，定義σ2=α×D，D為常數。

定義 P（OP′b|Bi）為在物流商b的底價為Bi時，分配給物流商b的利潤為OP′b時的概率，定義后驗概率為：

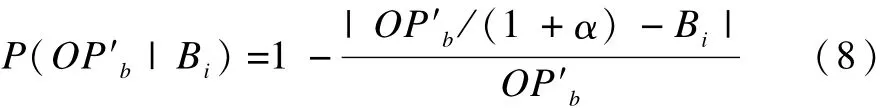
隨著協商的進行，被動企業可以根據協商的情況變更α的取值。α值越大時，代表物流商b的風險承受能力越高，其協商的耐心越大，|OP′b/（1+α）-Bi|越小，則P（OP′b|Bi）越大，此時假設集的概率分布越精確。

根據全概率公式：

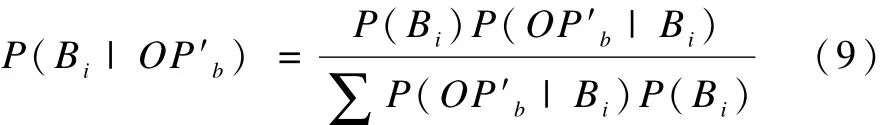
推算出物流商b的底價：

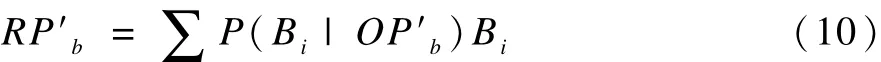
以該底價為基礎提報該報價方案（S-RP′b，RP′b）給協商Agent。

SteP3 被動物流商的反報價

被動物流商b的Agent從協商Agent收到報價方案（S-RP′b，RP′b）后，根據該方案同Step2的過程探索主動物流商a的底價RP′a，并根據該底價提出反報價方案（S-OP′b，OP′b）給主動物流商，其中，OP′b=（S-RP′b）（1+βb（t））。

SteP4 報價過程中的學習

通過以下的比較來學習和改進自己的報價方案：根據物流商的反報價方案（S-OP′b，OP′b），計算各物流商的滿意度。如果各個物流商的滿意度均為1，則直接按照該報價方案結束協商；如果各個物流商的滿意度不都為1，即假設對此時的反報價方案（S-OP′b，OP′b）計算各物流商的滿意度后，如果物流商的滿意度小于1，即仍為主動物流商，S-OP′b＜RP′a，則認為物流商a高估了物流商b的底價，此時變更主動物流商a的α的取值為：

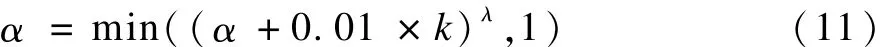
其中，K為連續主動協商的次數，當主動物流商多次為某一物流商時，該物流商的K=K+1；λ為主動物流商報價的變化速度。

如果物流商b的滿意度小于1，即OP′b＜RP′b，則認為低估了物流商b的底價，此時以物流商b為主動協商的物流商按照反報價方案（S-OP′b，OP′b）返回Step2繼續協商。

SteP5 協商次數限制

如果在規定的協商次數t內都未成功達成分配協議則進行人工干預。在Agent的協商過程中，也可以隨時進行人為調整報價參數以變更自己的報價策略從而進行干預。

3 應用實例

假設沒有歷史數據，所有的物流商都參與討價還價的流程。設定最大的協商次數為Tmax=120。以某汽車制造廠的2個進行運輸協同的物流公司為例，初始的利潤分配、各自的底價和報價參數如表1所示。

表1 初始利潤分配和底價元

由于初始分配給物流商A的利潤小于A的底價，因此按照式（5）其滿意度為0.904 19，此時物流商A對初始分配不滿，為主動物流商，需要對分配進行協商且急于獲取更多的利潤以達成協商，因此物流商A的耐心較小，需要以一個較大的初始λa值和wa值來對初始分配提出自己的報價，而此時物流商B為被動物流商，因此其耐心肯定大于物流商A。由于物流商B對初始分配的滿意度為1，其已經對現有分配滿意且希望獲取更多的利潤，因此其并不急于達成協商，耐心較大。設定物流商B的α=0.8，λ=0.5，下面計算主動物流商A提出的報價方案。

對于主動物流商A的Agent，按照式（2）計算得出初始報價參數為β（1）=（1-m in（1，600）/600）2× 1=0.983 4。設定式（6）中的參數q=5，N=100，式（7）中的參數D=100，按照式（6）求得物流商B的底價的可能值為｛1 383.59，1 483.59，1 583.59，1 683.59，1 783.59｝，按照式（7）求得對應的概率為｛0.054 5，0.244 2，0.402 6，0.244 2，0.054 5｝，按照式（8）求得后驗概率分別為｛0.947 6，0.966 1，0.984 6，0.996 9，0.978 3｝，按照式（9）求得概率為｛0.052 6，0.240 6，0.404 2，0.248 2，0.054 4｝，進而按照式（10）計算出此時物流商B的底價為1 584.70，物流商A的Agent按照該底價提出報價的分配方案為｛4 415.30，1 584.70｝。

對于物流商A提出的分配方案｛4 415.30，1 584.70｝，已知物流商A急于達成協商，屬于主動物流商，因此，設定物流商A的α=0.4，λ=2，來對該分配提出自己的反報價。和上述的物流商A的Agent計算方式相同，參數設定相同，求得物流商B反報價的分配方案｛3 706.16，2 293.84｝。

此時協調Agent以分配方案｛3 706.16，2 293.84｝作為當前方案廣播給所有物流商，再次判斷物流商A和物流商B對該方案的滿意度。同上述的計算過程，物流商A仍為主動物流商，物流商B為被動物流商，此時物流商A的按照式（11）變化為0.9，物流商A根據報價方案｛3 706.16，2 293.84｝提出新的報價方案｛4 792.72，1 207.28｝，物流商B提出反報價的方案｛4 041.21，1 958.79｝。此時對于該方案物流商A和B的滿意度為｛0.985 6，1｝。

物流商A仍為主動物流商，K=2，同上述計算過程物流商B提出反報價的方案｛4 213.82，1 786.18｝。此時對于該方案物流商A和B的滿意度為｛1，0.992 3｝。此時物流商B為主動物流商，K=0，重新進行協商。如此反復進行，當t=9時，反報價的方案｛4 177.36，1 822.64｝，此時對于該方案物流商A和B的滿意度均為1，達成協議，協商結束。總滿意度變化結果如圖4所示。

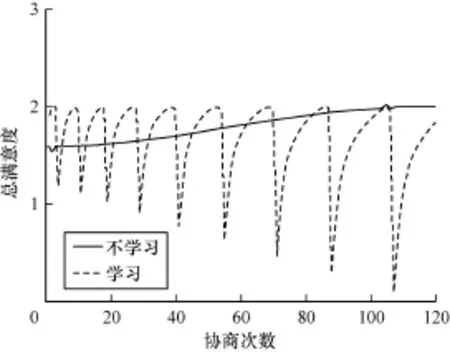
圖4 總滿意度比較

如圖4所示，當協商的物流商在報價過程中都不參與學習時，報價的滿意度是緩慢上升的，在t=109時，總滿意度之和為2，即協商結束。當參與學習時，報價曲線在t=9時，總滿意度之和為2，提高了報價協商的效率。因此，報價過程中的自學習可以有效地降低達成可以使得各方滿意的協同物流分配方案過程中的協商次數。同時從圖中的自學習總滿意度的變化曲線可以看出，總滿意度越接近2時，協商的次數越多，這是由于主動協商的物流商耐心增加，報價參數增加放緩，不同角色物流商協商次數增加。當總滿意度開始下降且未到達2時，則變化主動協商的預測參數和范圍并開始新一輪的討價還價。

如果將該報價結果和Rubinstein討價還價模型的結果進行比較，這里設定參與討價還價的物流商的貼現因子相同，均為0.8時，其協商過程中總滿意度的變化曲線如圖5所示。

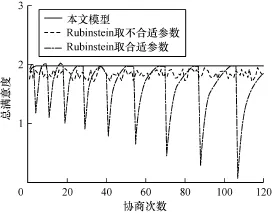
圖5 本文模型和Rubinstein模型的總滿意度比較

Rubinstein討價還價模型受主動協商物流商的還價設定的影響較大，一旦主動還價設定過高，使得主動協商物流商過快轉換角色，則可能陷入不斷轉換角色而很難達成協商的循環中，如圖5的Rubinstein取不合適參數值的曲線所示，當Rubinstein模型討價還價策略取不合適的參數值時，在最大的協商次數范圍內一直未能達成協商。而當Rubinstein模型討價還價策略取合適的參數值時，如圖5的Rubinstein取合適參數值的曲線所示，僅需要7次協商即可形成協商雙方滿意度都為1的利潤分配方案，但在實際應用中很難取到一個合適的還價值，還價值往往通過經驗判定，而采用本文模型時，協商總滿意度到2的速度取決于貼現因子，Agent自動探索對方底價和修正報價方案而無需人工經驗設定還價值，如圖5所示，共需要9次協商即可形成協商雙方滿意度都為1的利潤分配方案，從而避免了經驗判定所帶來的協商的不確定性。

當有多個物流商參與利潤分配時，根據圖1所示，在協調Agent發布初始利潤分配后，物流商根據各自的底價自行判斷自己的協商角色，將第一個主動物流商作為物流商A，將之后的所有物流商整體作為物流商B，應用2.3節中的自學習過程進行討價還價，得出滿意結果后再對物流商B內的物流商重復上述過程，這樣就將多個物流商討價還價的問題轉換為2個物流商討價還價的問題。

4 結束語

本文將協作物流商分為主動協商物流商和被動協商物流商，通過各物流商Agent對當前協商Agent分配報價方案的滿意度確定自己的主動或者被動地位。主動協商物流商通過探索被動協商物流商的底價來提出自己的報價方案，被動物流商通過探索主動協商物流商的底價來對主動物流商提出的報價方案給出反報價方案，通過協商次數和連續主動協商的影響不斷地修正自己的報價參數，從而提高協商效率，最終實現各方都滿意的協作利潤分配。應用實例結果證明其有效性。但本文并未考慮協商過程中的協商成本，且未考慮協商后發生違約時，再次協商時應予懲罰等情況，這些都是今后的研究重點。

［1］ Singh C，Sarkar S，A ram A，et al.Cooperative Profit Sharing in Coalition-based Resource Allocation in Wireless Networks［J］.IEEE/ACM Transactions on Networking，2012，20（1）：69-83.

［2］ 劉偉華，曲思源，鐘石泉.隨機環境下的三級物流服務供應鏈任務分配［J］.計算機集成制造系統，2012，18（2）：381-388.

［3］ 齊 源，趙曉康，李玉敏.基于Shaply值及Gahp的供應鏈知識共享收益分配研究［J］.科技進步與對策，2011，28（9）：132-137.

［4］ 孫多青，馬曉英.基于博弈論的多零售商參與下逆向供應鏈定價策略及利潤分配［J］.計算機集成制造系統，2012，18（4）：867-874.

［5］ 陳遠高，劉 南.具有服務差異的雙渠道供應鏈競爭策略［J］.計算機集成制造系統，2010，16（11）：568-575.

［6］ 肖 劍，但 斌，張旭梅.雙渠道供應鏈中制造商與零售商的服務合作定價策略［J］.系統工程理論與實踐，2010，30（12）：2203-2211.

［7］ 胡盛強，張畢西，劉繪珍，等.基于多方博弈的二級網狀供應鏈合作及利潤分配研究［J］.系統科學學報，2012，20（2）：48-51.

［8］ 李 勇，張 異，楊秀苔.供應鏈中制造商供應商合作研發博弈模型［J］.系統工程學報，2005，20（1）：12-18.

［9］ 姜能濤，古 貞.協同機制下供應鏈剩余利潤合理分配的影響因素研究［J］.物流工程與管理，2010，32（4）：97-100.

［10］ 韓建軍，郭耀煌.基于事前協商的動態聯盟利潤分配機制［J］.西南交通大學學報，2003，38（6）：425-433.

［11］ 周 揚，石巋然.制造商主導的供應鏈合作及利潤分配研究［J］.科技管理研究，2012，31（5）：136-140.

［12］ 潘會平，陳榮秋.供應鏈合作的利潤分配機制研究［J］.系統工程理論與實踐，2005，25（6）：568-572.

［13］ Bremer J，Sonnenschein M.Estimating Shapley Values for Fair Profit Distribution in Power Planning Smart Grid Coalitions［C］//Proceedings of International Conference on Multiagent System Technologies.Berlin，Germ any：Springer，2013：208-221.

［14］ Pinto T，Morais H，Oliveira P，et al.A New Approach for Multi-agent Coalition Formation and Management in the Scope of Electricity Markets［J］.Energy，2011，36（8）：5004-5015.

［15］ 蔣國瑞，龐 婷.基于多Agent供應鏈協同的自適應協商方法［J］.計算機工程，2014，40（3）：188-192.

編輯 劉冰

Collaborative Logistics Profit Distribution Model Based on Agent

TIAN Ran，HAN Min，LIBinyong
（School of Information Science and Technology，Southwest Jiaotong University，Chengdu 610031，China）

For the problem of uncertainty of negotiation caused by the parameters setting in the Rubinstein profit distribution model are mostly from the artificial experience，a self learning model of profit distribution is established for this problem.The model divides logistic providers to active collaborative logistics provider and passive collaborative logistics provider.Different types of collaborative logistics providers propose offer or counter offer by exploring the other logistics provider's base price，decide whether to change the role type by current offer results，changes the strategy of quotation in quotation process by self learning quotation parameters，and gets the satisfactory results for all parties. Simulation results show that this model can reduce the number of negotiation times，and can effectively avoid the negotiation uncertainty of experience judgment com pared with the Rubinstein profit distribution model.

transportation economy；profit distribution；pricing strategy；collaborative logistics；bargaining strategy

田 冉，韓 敏，李斌勇.基于Agent的協同物流利潤分配模型［J］.計算機工程，2015，41（9）：286-291.

英文引用格式：Tian Ran，Han M in，Li Binyong.Collaborative Logistics Profit Distribution Model Based on Agent［J］. Computer Engineering，2015，41（9）：286-291.

1000-3428（2015）09-0286-06

A

TP391

10.3969/j.issn.1000-3428.2015.09.053

國家“863”計劃基金資助項目“汽車及工程機械多產業鏈業務協同服務平臺研發”（2013AA 040606）。

田 冉（1981-），男，博士研究生，主研方向：智能計算，決策支持系統；韓 敏，副研究員、博士；李斌勇，博士研究生。

2014-07-11

2014-08-06 E-m ail：troom@163.com