SPH并行計算方案及其在自由表面流動模擬中的應(yīng)用*

周 浩，徐志宏，鄒 順，湯文輝

(1.國防科技大學(xué) 理學(xué)院， 湖南 長沙 410073； 2.國防科技大學(xué) 計算機(jī)學(xué)院， 湖南 長沙 410073)

SPH并行計算方案及其在自由表面流動模擬中的應(yīng)用*

周 浩1，徐志宏1，鄒 順2，湯文輝1

(1.國防科技大學(xué) 理學(xué)院， 湖南 長沙 410073； 2.國防科技大學(xué) 計算機(jī)學(xué)院， 湖南 長沙 410073)

針對光滑粒子動力學(xué)主要計算量是近鄰粒子搜索這一特點(diǎn)，提出了一種基于粒子分解的光滑粒子動力學(xué)并行計算方案。利用該方案可以方便地將任意串行光滑粒子動力學(xué)代碼并行計算，而且每一個時間步內(nèi)的信息傳遞量只和粒子總數(shù)有關(guān)，而和粒子的分布無關(guān)，因而特別適合于自由表面流動等大變形問題的并行數(shù)值模擬。對一個粒子總數(shù)為40萬的三維潰壩問題的模擬結(jié)果表明：此方案能達(dá)到的最大加速比約為16，這一結(jié)果可能比空間分解方案(不考慮動態(tài)負(fù)載均衡)更優(yōu)。

光滑粒子動力學(xué)；并行方案；粒子分解；空間分解

(1.CollegeofScience,NationalUniversityofDefenseTechnology,Changsha410073,China；

2.CollegeofComputer,NationalUniversityofDefenseTechnology,Changsha410073,China)

多數(shù)數(shù)值方法在處理大變形時存在一定困難。光滑粒子動力學(xué)(SmoothedParticleHydrodynamics,SPH)[1-2]方法作為一種無網(wǎng)格的拉格朗日方法，在處理自由表面流動等大變形問題時具有很大的優(yōu)勢，近年來其應(yīng)用已經(jīng)擴(kuò)展到很多領(lǐng)域。又因?yàn)樗睦窭嗜仗匦裕缑娓浇镔|(zhì)的運(yùn)動即代表了界面的運(yùn)動，因此處理多相流也比較自然，且不需要額外的界面追蹤算法。但是，SPH方法比有限差分、有限元等網(wǎng)格方法的計算量要大，因此在模擬規(guī)模較大的問題時經(jīng)常需要并行計算。

SPH的計算過程和分子動力學(xué)(MolecularDynamics,MD)類似，所以其并行也和MD類似。Plimpton[3]總結(jié)了3種不同的MD并行方案，即空間分解，粒子分解和力分解。目前，文獻(xiàn)中絕大多數(shù)SPH方法并行采用的都是空間分解方案，因?yàn)槠湫畔鬟f量小，其缺點(diǎn)是編程實(shí)現(xiàn)復(fù)雜。

空間分解方案又可以分為靜態(tài)和動態(tài)兩種。靜態(tài)空間分解時，每個處理器分配的空間始終固定。當(dāng)所有粒子始終在計算域近似均勻分布時，這種方法能夠得到極高的加速比。但是，在自由表面流動等實(shí)際問題中，粒子往往在空間中分布非常不均勻，這會使得負(fù)載嚴(yán)重不平衡，導(dǎo)致加速比較小。動態(tài)空間分解時，需要根據(jù)負(fù)載平衡原則每隔一段時間動態(tài)調(diào)整各個處理器空間的大小和位置，來保證所有處理器的計算量大致相等。調(diào)整處理器空間需要額外的計算時間，因此動態(tài)調(diào)整的頻率要適當(dāng)，而且調(diào)整算法也必須高效。

動態(tài)空間分解雖然能夠高效地模擬大變形問題，但是實(shí)現(xiàn)起來非常復(fù)雜。如Ferrari等[4]在采用并行SPH方法模擬三維潰壩問題時，采用第三方軟件包METIS來動態(tài)調(diào)整處理器空間。在METIS中，首先需要在空間布滿背景網(wǎng)格，再根據(jù)每個小網(wǎng)格中粒子數(shù)的多少來給每個小網(wǎng)格一個權(quán)重，來實(shí)現(xiàn)每個處理器空間大小不等但是計算量近似相等，用以實(shí)現(xiàn)負(fù)載平衡。Marrone等[5]采用并行SPH方法模擬行船產(chǎn)生的波浪及其破碎時，只在主要流動方向上動態(tài)調(diào)整，因?yàn)檫@能極大地簡化編程，并且指出存在主要流動方向的特征越明顯，并行模擬的加速比越高。并行SPH程序JOSEPHINE[6]和開源軟件parallelSPHYSICSv2.0在模擬二維自由表面流動時，也都只在一個主要流動方向上實(shí)現(xiàn)了動態(tài)調(diào)整，因此，當(dāng)流動有多個主要方向時，加速比會下降。總的來說，動態(tài)空間分解的實(shí)現(xiàn)復(fù)雜度嚴(yán)重限制了其在SPH并行模擬中的廣泛使用。

Plimpton描述了MD的粒子分解并行方案，其基本思想是每個處理器負(fù)責(zé)維護(hù)固定的某一部分粒子。這種方案的最大優(yōu)點(diǎn)在于并行很容易在串行代碼的基礎(chǔ)上實(shí)現(xiàn)[3]。但是，由于MD中的分子由若干原子組成，分子具有一定內(nèi)部結(jié)構(gòu)，需要考慮其旋轉(zhuǎn)等因素，而且與每個分子有相互作用的分子列表可以若干時間步更新一次，所以其主要計算量在于分子間相互作用力的計算。而SPH中粒子間的相互作用力相對簡單，而且一般每個時間步都需要更新每個粒子的近鄰粒子，因此其主要計算量在于近鄰粒子搜索[7]。

針對SPH方法的上述特點(diǎn)，提出了一種簡單的粒子并行方案。這種方案能夠達(dá)到可觀加速比，有效節(jié)約計算時間，而且方案實(shí)現(xiàn)非常簡單，負(fù)載均衡，每個時間步的信息傳遞量與粒子分布無關(guān)，可以十分方便地采取任意奇數(shù)個處理器并行計算。但是，這種方案的信息傳遞量較大，不適合上百個處理器的大規(guī)模并行計算。

以二維圓柱繞流和三維潰壩問題為例，比較了這種粒子并行方案和空間分解方案(不考慮動態(tài)負(fù)載均衡)的計算時間或加速比。在這兩個算例中，前者粒子分布始終非常均勻，而后者則是典型的大變形問題，粒子分布嚴(yán)重不均勻。這兩個算例的對比可以明顯地展示出粒子并行方案只適合于粒子分布嚴(yán)重不均勻問題的并行模擬。SPH靜態(tài)空間分解方案在開源軟件平臺OpenFOAM的基礎(chǔ)上實(shí)現(xiàn)，粒子分解方案采用Fortran90語言加上訊息傳遞接口(MessagePassingInterface，MPI)消息傳遞庫實(shí)現(xiàn)。本文所有模擬都是在廣州超算中心的天河二號計算機(jī)上完成。

1 控制方程及其SPH離散

假設(shè)系統(tǒng)中沒有溫度梯度，黏性流動的控制方程為如下N-S方程

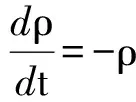
(1)

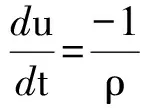
(2)

其中:ρ，u,p,t分別為密度、速度、壓力和時間；υ2u為黏性力；υ為運(yùn)動黏性系數(shù)；fe為外力。控制方程式(1)和式(2)右邊各導(dǎo)數(shù)項(xiàng)的SPH離散形式如下：

(-ρ

(3)

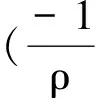
(4)

(5)

其中，式(5)為Morris基于有限差分和SPH離散提出的黏性力計算模型[8]。本文模擬中時間積分采用蛙跳法。

對不可壓縮流體采用弱可壓來近似，通過將流體的密度變化控制在1%以內(nèi)來近似實(shí)現(xiàn)不可壓[9]。本文中采用如下最常用的物態(tài)方程其中，γ=7，c0取粒子最大速度的10倍。

(6)

2 SPH并行方案

現(xiàn)階段文獻(xiàn)中SPH并行絕大多數(shù)采用的是空間分解方案。本文實(shí)現(xiàn)并比較了空間分解和粒子分解這兩種并行方案各自的優(yōu)缺點(diǎn)。

2.1 空間分解方案

空間分解方案是目前使用最普遍的方案，其基本思想就是首先將整個計算域劃分為若干不重疊的子域，然后每個處理器負(fù)責(zé)一個子域，如圖1所示。

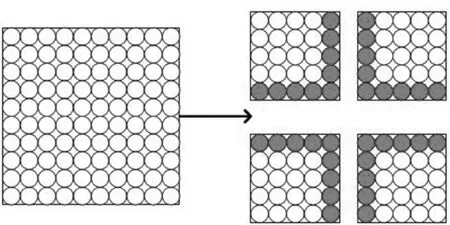
圖1 空間分解示意圖Fig.1 Domain decomposition

當(dāng)計算滿足局域性(任何一點(diǎn)在下一時刻的值只和包括這點(diǎn)的某局部空間相關(guān))時，只有在子域之間的交界處才需要傳遞信息，如圖1中的實(shí)心粒子部分。因此，劃分子域的一個原則就是讓交界面積盡量小，這代表了信息傳遞少，即并行帶來的額外時間開銷小。另一個原則是盡量保持每個子域的計算量相等，即負(fù)載均衡，這樣才能達(dá)到較高加速比。

在歐拉類網(wǎng)格方法中，往往是網(wǎng)格的數(shù)量代表了計算量。由于網(wǎng)格是不動的，所以負(fù)載均衡比較容易實(shí)現(xiàn)。但是SPH方法屬于拉格朗日方法，粒子數(shù)量大致代表了計算量，大變形條件下，粒子占據(jù)的空間可能發(fā)生很大變化，如模擬潰壩、氣體擴(kuò)散、超高速碰撞等問題。這會導(dǎo)致每個子域的粒子數(shù)量嚴(yán)重不平衡，導(dǎo)致并行效率低下。一種做法是采取動態(tài)負(fù)載均衡，即模擬過程中如果發(fā)現(xiàn)負(fù)載不均衡，就按照一定策略將空間重新分解，如開源軟件parallelSPHYSICSv2.0的使用手冊中給出的二維潰壩問題的模擬結(jié)果，其動態(tài)負(fù)載均衡如圖2所示。

圖2 動態(tài)負(fù)載均衡Fig. 2 Dynamic load balancing

圖2中有3個垂直方向的處理器邊界，它們將整個計算域劃分為4個子域，每個子域用一個處理器計算。當(dāng)粒子整體向右移動時，每個處理器邊界也適當(dāng)向右移動，來盡量保證每個子域的粒子數(shù)相等。

動態(tài)空間分解雖然能夠解決負(fù)載不均衡問題，但是實(shí)現(xiàn)起來復(fù)雜，所以本文不考慮動態(tài)空間分解。

2.2 粒子分解方案

本文針對SPH方法的主要計算量在于近鄰粒子搜索這一特點(diǎn)，提出并實(shí)現(xiàn)了一種新的粒子分解方案，其基本思想是將找出所有近鄰粒子對這樣一個大任務(wù)劃分為np(處理器數(shù))個小任務(wù)，每個處理器完成一個。

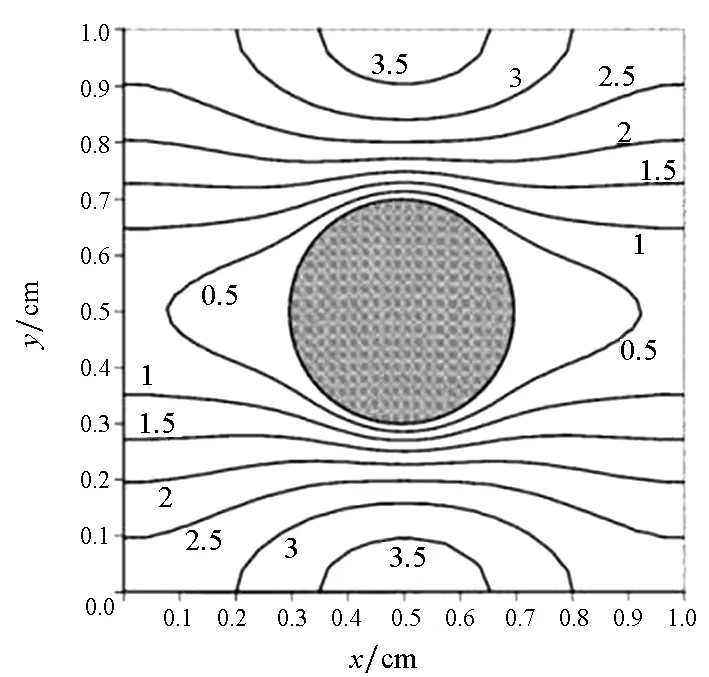
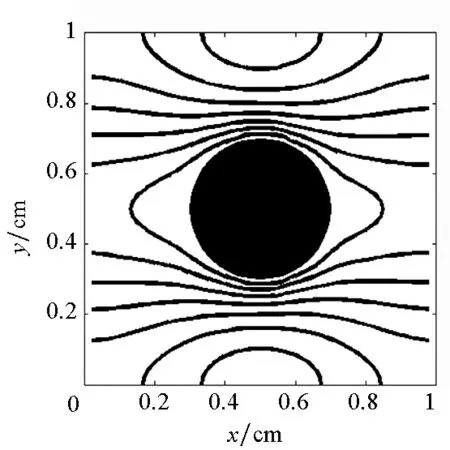
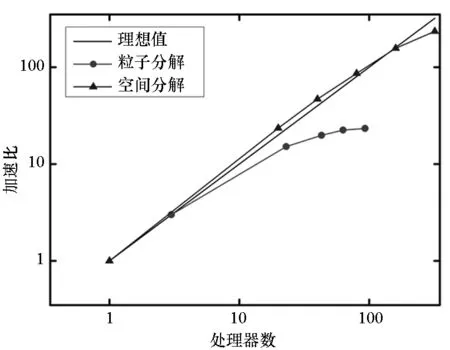
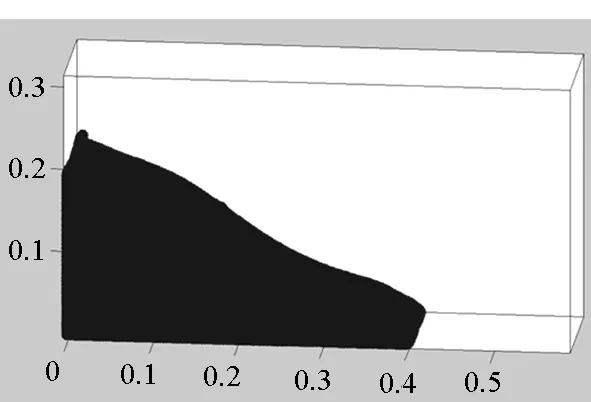
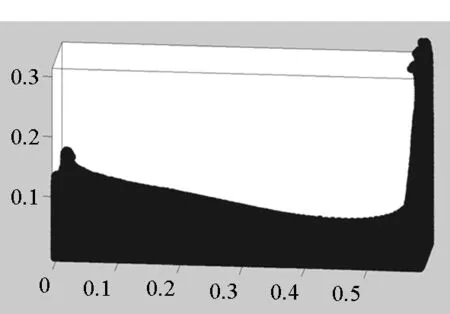
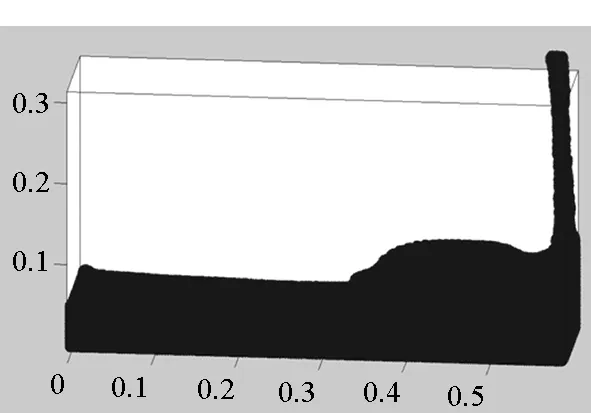
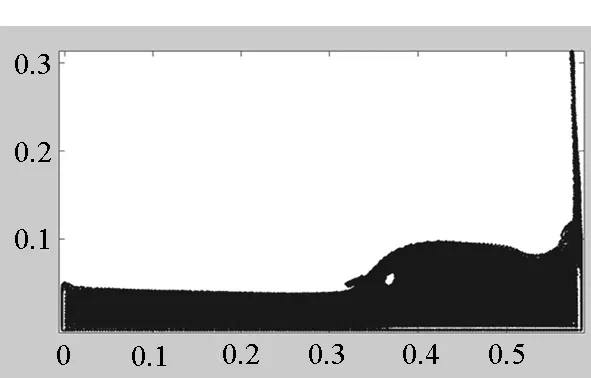
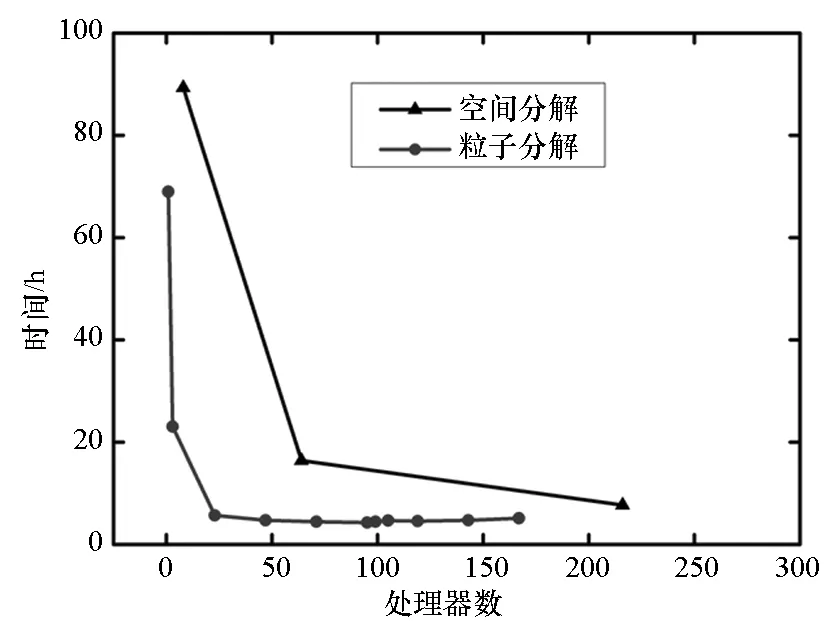
首先將所有粒子依據(jù)編號從小到大分為np個組Gm(m=1,2,…,np)，每個組的粒子數(shù)近似相等，約為N/np(其中N為粒子總數(shù))，處理器m維護(hù)組Gm。當(dāng)粒子i和粒子j是近鄰粒子時，可以用(i,j)來表示這一近鄰粒子對，為了避免重復(fù)，因此要求i

由于m≤n，可知子集(Gm,Gn)有np(np+1)/2個，且相互不重疊。每個處理器負(fù)責(zé)(np+1)/2個。顯然，當(dāng)np為奇數(shù)時，(np+1)/2為整數(shù)，此時，每個處理器的負(fù)載非常均衡。下面以np=5為例來說明這些子集在處理器上的分配策略，如表1所示。

表1 近鄰粒子對在不同處理器之間分配策略

由表1可以看到，處理器P1負(fù)責(zé)維護(hù)G1這組粒子。在每個時間步長內(nèi)，P1首先需要將G1組粒子的所有信息發(fā)送給P4和P5，因?yàn)镻4需要找出近鄰粒子對子集(G1,G4)，P5需要找出(G1,G5)；然后P1搜索被分配的近鄰粒子對(本文采用樹搜索算法)并同時計算相互作用力；最后P4和P5將所計算的G1組粒子受到的部分作用力發(fā)送回P1，由P1更新G1這組粒子的狀態(tài)。

處理器P2的計算過程類似，即P2首先將G2組粒子的所有信息發(fā)送給P1和P5；然后尋找被分配的近鄰粒子對并同時計算相互作用力；最后P1和P5將所計算的G2組粒子受到的部分作用力發(fā)送回P2，由P2更新G2這組粒子的狀態(tài)。其他處理器的計算過程也類似。

于是，每個時間步可以分為如下4步：粒子信息發(fā)送、近鄰粒子搜索并同時計算粒子間相互作用力、相互作用力信息交換和更新粒子狀態(tài)。分別統(tǒng)計每步的計算時間，可以得到：第1步和第3步為信息傳遞，時間隨著處理器的增加而緩慢增加；第2步是主要計算量，隨著處理器的增加而單調(diào)減小；第4步也是計算，時間幾乎可以忽略不計[10]。

可以看到，本粒子分解方案有如下特點(diǎn)：①一個時間步長內(nèi)的所有通信為每個處理器調(diào)用一次廣播函數(shù)和一次求和歸約函數(shù)，實(shí)現(xiàn)非常簡單；②每個處理器的計算量和通信量都大致相等，負(fù)載非常均衡；③每步的信息傳遞量為O(N)，與粒子的分布無關(guān)；④可以十分方便地采取任意奇數(shù)個處理器并行計算。

3 兩種并行方案的比較

3.1 二維圓柱繞流

模型參數(shù)與文獻(xiàn)[8]中的圓柱繞流算例一致，雷諾數(shù)為0.03。初始時，X方向和Y方向各均勻分布1000個粒子，總粒子數(shù)為100萬。X方向?yàn)橹芷谛赃吔鐥l件，對應(yīng)的實(shí)際物理問題為無限長管道中均勻分布無數(shù)個圓柱。圖3給出了SPH模擬結(jié)果和有限元模擬結(jié)果的對比，其中圖3(a)為文獻(xiàn)[8]中的有限元模擬結(jié)果，圖3(b)為本文模擬結(jié)果。

(a)有限單元法(a)Finte Elmemt Modeling

(b) 光滑粒子動力學(xué)(b)Smoothed particle hydrodynamics圖3 SPH和有限元模擬的速度大小等值線對比Fig.3 Contour lines of velocity magnitude using FEM and SPH for Re=0.03

分別采取兩種并行方案，測得的加速比如圖4所示。

圖4 空間分解和粒子分解加速比隨處理器的變化Fig. 4 Speed-up ratio of domain decomposition and particle decomposition with the change of processors

從圖4可以看到，空間分解時，當(dāng)處理器數(shù)目在小于100時，加速比反常地略高于理想值，其原因可能和緩存等硬件有關(guān)，文獻(xiàn)[4-5]以及開源軟件parallelSPHYSICSv2.0使用手冊中都報告了類似的情況。當(dāng)處理器數(shù)目為320時，加速比約為234.69，并行效率為73.34%。如果繼續(xù)增加處理器數(shù)至640，加速比迅速降低為100.13，對應(yīng)的并行效率為15.65%，因此結(jié)果沒有在圖4中給出。

粒子分解時，最多采用了93個處理器，此時的加速比為23.33，并行效率為25.09%。如果繼續(xù)增加處理器數(shù)量，加速比則緩慢下降。

因此，對于粒子分布均勻的情況，空間分解的加速比遠(yuǎn)大于粒子分解。而且可以發(fā)現(xiàn)，粒子分解不適合上百個處理器的大規(guī)模并行計算。

3.2 三維潰壩問題

模型參數(shù)與文獻(xiàn)[11]中的潰壩算例一致，初始水柱高0.292m，寬0.146m，容器寬度為0.584m。初始粒子總數(shù)大約為40萬，時間步長固定為20μs，共計算了50 000個時間步長。圖5為文獻(xiàn)[11]給出的二維流體體積法(VolumeOfFluid，VOF)模擬結(jié)果，從左到右的時刻依次為0.2s，0.4s，0.6s和0.8s。

圖5 潰壩問題的二維模擬結(jié)果[10]Fig. 5 2D VOF simulation of dam break

本文采用靜態(tài)空間分解和粒子分解兩種不同的并行方案對同樣的問題進(jìn)行了三維數(shù)值模擬。模擬的粒子分布如圖6所示。

(a) t=0.2s

(b) t=0.4s

(c) t=0.6s

(d) t=0.8s圖6 三維潰壩問題的SPH模擬Fig. 6 3D SPH simulation of dam break

可以看到，三維模擬結(jié)果和文獻(xiàn)[11]中的實(shí)驗(yàn)及VOF模擬結(jié)果基本一致。為了和二維模擬結(jié)果對比，圖7給出了0.8s時刻粒子分布的一個二維視圖。

圖7 0.8s時刻的二維視圖Fig.7 2D view point at t=0.8s

從圖7可以看到，流體在0.8s時刻形成了一個空腔，這和VOF計算結(jié)果吻合。

因?yàn)槿萜髟赬，Y，Z方向上的尺寸約為1∶4∶2，因此在空間分解時，X，Y，Z方向上的處理器個數(shù)取為n，4n，2n，從而讓每個處理器分配的空間大小近似相等，總處理器個數(shù)為8n3。但是由于粒子在整個容器中的分布極不均勻，每個處理器上分配的粒子數(shù)實(shí)際上極不均勻，甚至多數(shù)處理器上沒有粒子。本算例中，空間分解時處理器個數(shù)分別取為8，64，216，分別對應(yīng)于n=1，2，3。

兩種并行方案測得的計算時間如圖8所示。

圖8 空間分解和粒子分解計算時間隨處理器的變化Fig.8 Total computing time of domain decomposition and particle decomposition with the change of processors

可以看到，空間分解的計算時間比粒子分解要長，而且計算時間隨處理器數(shù)的增加緩慢下降。當(dāng)處理器數(shù)為216時，空間分解需要約7.7h，加速比為9.0。此處加速比定義為speedup=T1/Tn，其中Tn為采用n個處理器并行計算的時間，T1為串行計算時間。由于空間分解程序的計算時間較長，沒有測試其串行計算時間，所以其串行計算時間采用粒子分解程序的串行時間。計算中還發(fā)現(xiàn)，當(dāng)處理器數(shù)為216時，絕大多數(shù)處理器中沒有粒子，這是由潰壩問題中粒子分布不均勻的特點(diǎn)以及沒有動態(tài)負(fù)載均衡造成的。

粒子分解時，當(dāng)處理器數(shù)為23時，計算時間為5.7h，幾乎已經(jīng)降到最低值，且計算時間比空間分解方案的最優(yōu)值少。當(dāng)處理器數(shù)為95時，需要的時間最少，為4.3h，最大加速比為16.1。如果繼續(xù)增加處理器數(shù)，計算時間緩慢增加。

4 結(jié)論

本文提出了一種非常簡單的基于粒子分解的SPH并行方案，并以二維圓柱繞流和三維潰壩問題的SPH并行模擬為例，比較了粒子分解和空間分解的計算時間或加速比，得到了以下主要結(jié)論：

1)當(dāng)粒子分布均勻時，SPH并行應(yīng)該采用空間分解方案。此時，只有處理器邊界處有信息傳遞，信息傳遞量小，能夠達(dá)到非常大的加速比。而粒子分解的加速比相對較小。

2)當(dāng)粒子分布非常不均勻時，SPH并行可以采用粒子分解方案。此時，靜態(tài)空間分解的負(fù)載嚴(yán)重不平衡，導(dǎo)致加速比較小。而粒子分解采用較少處理器就能達(dá)到可觀加速比。

3)從文中兩個算例可以看出，當(dāng)問題規(guī)模在40萬～100萬左右時，粒子分解方案的加速比固定在16～23左右。在粒子分布非常不均勻的情況下，這一結(jié)果可能比靜態(tài)空間分解更優(yōu)。因而，本文提出的粒子分解方案在自由表面流動模擬中具有一定優(yōu)勢。

References)

[1]LucyLB.Anumericalapproachtothetestingofthefissionhypothesis[J].AstronomicalJournal, 1977, 82: 1013-1024.[2]MonaghanJJ,GingoldRA.ShocksimulationbytheparticlemethodSPH[J].JournalofComputationalPhysics, 1983, 52(2): 374-389.

[3]PlimtonS.Fastparallelalgorithmsforshort-rangemoleculardynamics[J].JournalofComputationalPhysics, 1995, 117(1): 1-19.

[4]FerrariA,DumbserM,ToroEF,etal.Anew3DparallelSPHschemeforfreesurfaceflows[J].Computers&Fluids, 2009, 38(6): 1203-1217.

[5]MarroneS,BouscasseB,ColagrossiA,etal.Studyofshipwavebreakingpatternsusing3DparallelSPHsimulations[J].Computers&Fluids, 2012, 69: 54-66.

[6]CherfilsJM,PinonG,RivoalenE.JOSEPHINE:aparallelSPHcodeforfree-surfaceflows[J].ComputerPhysicsCommunication, 2012, 183(7): 1468-1480.

[7]MoulinecC,IssaR,LatinoD,etal.High-performancecomputingandsmoothedparticlehydrodynamics[C]//ProceedingsofParallelComputationalFluidDynamics,Lyon, 2008.

[8]MorrisJP,FoxPJ,ZhuY.ModelinglowreynoldsnumberincompressibleflowsusingSPH[J].JournalofComputationalPhysics, 1997, 136(1): 214-226.

[9]MonahanJJ.SimulatingfreesurfaceflowswithSPH[J].JournalofComputationalPhysics, 1994, 110(2): 399-406.[10] 周浩，湯文輝，冉憲文，等. 光滑粒子流體動力學(xué)的一種并行數(shù)值計算方案[J]. 航天器環(huán)境工程， 2012， 29(1): 23-26.ZHOUHao,TANGWenhui,RANXianwen,etal.Spacecraftenvironmentengineering[J].SpacecraftEnvironmentEngineering, 2012, 29(1): 23-26.(inChinese)[11]DoringM,AndrillonA,AlessandriniB,etal.SPHfreesurfaceflowsimulation[C]//Proceedingsofthe18thInternationalWorkshoponWaterWavesandFloatingBodies,LeCroisic, 2003.

SPH parallel schemes and its application in free surface flow simulation

ZHOU Hao1, XU Zhihong1, ZOU Shun2, TANG Wenhui1

Forthemaincomputationofsmoothedparticlehydrodynamicswasfinitenearestparticlesearch,anovelschemetoparallelizethesmoothedparticlehydrodynamicsmethodbasedontheconceptofparticledecompositionwasproposed.Anyserialsmoothedparticlehydrodynamicscodecouldbeeasilyparallelizedbyusingtheproposedscheme.Theamountofinformation,whichwastransformedineachtimestep,dependedonlyonthetotalnumberofparticles,butnotonthespatialdistributionofparticles.Therefore,theproposedschemewasparticularlyusefulfortheparallelsimulationofcasesinvolvedviolentfreesurfacemovements.Fromthesimulationresultsofa3Ddambreakcasewithatotalnumberof0.4million,theproposedschemecanachieveaspeedupratioabout16,whichprovesthattheproposedschememaybeisbetterthanthedomaindecompositionscheme(withoutconsideringdynamicloadbalance).

smoothedparticlehydrodynamics;parallelscheme;particledecomposition;domaindecomposition

2014-07-08

國家自然科學(xué)基金資助項(xiàng)目(61221491，61303071)，廣州科信局基金資助項(xiàng)目(134200026)

周浩(1986—)，男，湖南常德人，博士研究生， E-mail: zhouhao12029014@163.com；湯文輝(通信作者)，男，教授，博士， 博士生導(dǎo)師，E-mail：wenhuitang@163.com

10.11887/j.cn.201504012

http://journal.nudt.edu.cn

TB

A