大班數學學習困難兒童數學操作游戲干預的研究

李正清+周欣+田麗麗+康丹+徐晶晶

【摘要】本研究通過數學操作游戲對兩名大班數學學習困難兒童關于“阿拉伯數字系統”的掌握以及“數的部分與整體關系”的理解進行干預。結果表明，干預后被試兒童這兩方面的數學能力均有不同程度的提高。研究提示我們，完善“數字系統”——積累“數的分合”經驗——發現“數的分合”規律——運用“數的分合”知識，可能是一條對早期數學學習困難兒童進行干預的有效途徑。

【關鍵詞】早期數學學習困難兒童;游戲干預;個案

【中圖分類號】G610 ? 【文獻標識碼】A ? 【文章編號】1004-4604（2015）10-0024-06

本研究中，早期數學學習困難（Mathematics learning difficulty）兒童是指智力發展正常，但數學發展水平顯著低于同齡兒童的5～6歲兒童。早期數學學習困難的診斷并非是早早地給這些兒童貼上一個負面標簽，而是要盡早查找其發展水平低下的原因，并提供有針對性的早期干預。〔1〕有研究表明，越早發現并盡早實施干預，就越能有效地幫助這些兒童。〔2〕

兒童早期的數學學習困難常常會出現負面累積效應，即隨著時間的推移，其與同伴的發展水平差距越來越大，〔3〕到小學后再實施干預則往往為時已晚。〔4〕成長模型研究表明，學前班秋季和春季兩個學期中數學得分均偏低的兒童，隨后4～5年的數學學習發展速率和數學成績也往往很低。數學學習困難兒童緩慢的成長速度與他們不理解數字集合、不能進行加法事實提取、不常使用分解策略有關。〔5〕我們前期的干預研究也發現，數學學習困難兒童對“數的部分與整體關系”存在一定的理解障礙，在干預過程中進步緩慢。并且，即使掌握了部分“數的分解與組合”知識，他們在加減運算中也不會主動運用這類知識，而仍然傾向于使用“數手指”等方法。〔6〕

本研究以數學操作游戲為手段，嘗試通過完善數學學習困難兒童的數字系統及引導其通過自主操作，幫助其逐步建構起對“數的部分與整體關系”的理解，進而改善其數學能力。同時，探討和總結對類似兒童進行個別訓練與教育的有效方法。

一、研究設計

（一）被試的選取與鑒定

L，女，開始干預時月齡68個月，身體健康，無重大疾病史。父母均為大專文化水平，重視教育。家庭經濟條件良好，與父母、祖父母一起生活。L喜歡參與繪畫美工活動，性格開朗，社會性發展良好，樂于為集體服務。據帶班老師描述，在幼兒園集體活動中，L反應速度一般，表現不甚積極，學習能力一般，數學能力較弱。

Y，女，開始干預時月齡73個月，身體健康，無重大疾病史。父母均為高中文化水平，家庭經濟條件一般，家庭教養方式較為溺愛。Y性格開朗，語言發展較好，運動水平較高，社會交往能力較強，較受同伴歡迎。據帶班老師描述，在幼兒園集體活動中，Y注意力時常不集中，學習欲望缺乏，數學能力較差。

L和Y是帶班老師認定的“班上數學學習和發展最為緩慢”的兒童。研究者對其進行智商和數學能力測查。使用《韋氏學前兒童智力量表》（Wechsler preschool and primary scale of intelligence，以下簡稱WPPSI）對L和Y進行測查，發現兩名兒童的智商均屬于正常水平。使用兒童早期數學能力測驗（Test of early mathematics ability，以下簡稱TEMA）對上海市普陀區三所幼兒園的大班兒童（N=339）進行數學能力測試，將數學能力分數排名在最后10%以內（臨界值為104 分）的兒童確認為數學學習困難兒童。經測查和對比，研究者發現，L和Y的智力正常，但數學能力分數均低于104分，因此可視為數學學習困難兒童。在我們最終確定的全部數學學習困難兒童樣本中（N=63;TEMA能力分M=95.97，SD=7.20），L的TEMA得分恰好等于數學學習困難兒童的篩選臨界分數，也即高于數學學習困難組兒童的平均分數，可以說，其數學學習困難程度相對較輕;Y的TEMA得分比平均分數低了一個標準差，可以說，其數學學習困難程度相對較重。

（二）研究工具

由一位經過培訓的學前教育專業研究生對L和Y進行干預前和干預后的測查。所有測查項目以一對一的形式在安靜的幼兒園活動室里進行。干預前的測查在當年9月實施，干預后的測查在次年6月實施。

1.《早期兒童數學能力測驗量表》（TEMA）

該量表是Ginsburg和Baroody修訂的版本，是測查3～8歲兒童數學能力的標準化工具，也可以用來鑒別數學學習困難兒童。量表共72個項目，每個項目計1分。〔7〕課題組對量表進行了漢化，經檢驗，中文版量表具有良好的效度和信度。〔8〕

2.《中國-韋氏幼兒智力量表》（WPPSI）

該量表分言語和操作測驗兩部分，言語部分測驗包括知識、分類、算數、詞匯、理解、背數6個部分;操作部分測驗分為填圖、排列、積木、拼圖、譯碼、迷津6個部分。每項測驗均按照計分手冊要求單獨計分。語言量表、操作量表和全量表均分別求得智商分數。運用中國常模對測查結果進行分數轉換。根據規定，在選取數學學習困難兒童時，排除智商分數低于80分的兒童。

（三）干預思路與計劃

1.干預內容

有研究表明，數概念是兒童數學能力發展中的一個“中心概念”，它的發展不僅與兒童今后的數學學習直接相關，而且與兒童的思維能力發展有著密切聯系。〔9〕兒童對數量集合的理解是其數概念發展的一項重要內容，要基于其對數詞系統的掌握和對數的部分與整體關系的理解。兒童對數量集合的理解能夠比一般認知學習能力更好地預測其數學學業成就，〔10〕因此，可以作為數學學習困難的篩查工具。〔11〕為此，本研究重點對被試兒童的數概念，主要包括阿拉伯數字系統、數的部分與整體關系進行干預。

數字系統是兒童早期數知識學習的一個最重要工具，對數字符號的掌握是兒童在表征水平上理解抽象數字系統要做到的第一步。研究表明，兒童的唱數水平與其數數技能和對數的理解有直接的關系，兒童掌握的數字鏈的長短可作為其數概念發展水平的重要標志之一。兒童對數字的掌握與其成熟、經驗水平有關，兒童阿拉伯數字系統的習得在很大程度上受練習機會的影響。因此，如能在干預過程中提供大量的練習機會，數學學習困難兒童還是有可能進一步完善其數字系統的。〔12〕

數的部分與整體關系是指數的相加性組成原理，即任何自然數可以分成更小的數，也可以與其他的數組合成更大的數，在心理學中被稱為部分-整體圖式（Part-whole scheme）。它是兒童早期數學發展中一個極為重要的認知發展內容，也是兒童掌握數概念的一個重要內容，在加減運算中具有重要作用。這種對數的理解能夠幫助兒童識別運算所涉及的數之間的部分與整體的關系，并運用這些關系去選擇正確的運算方法，尤其是使兒童在不能直接用實物演示題目的情境中也有可能解題。〔13〕研究表明，兒童6歲時已基本理解這一關系，6歲半時則能夠完全掌握。〔14〕因此，通過干預完全有可能讓數學學習困難兒童理解這一關系。

2.干預策略

建構主義強調學與教過程中學習者的主動參與、自主學習和意義建構，認為情境、協作、會話和意義建構是學習環境的四大要素。因此，本研究通過數學操作游戲，為被試兒童創設有意義的問題情境，并通過與同伴、研究者的相互溝通、平等交流，構建一個學習共同體，以引導被試兒童進行相關探索、自我調節和意義建構。

3.干預計劃

正確及熟練地數數是理解數的部分與整體關系的前提。因此，本研究先對被試兒童進行數數的干預，隨后進行數的部分與整體關系的干預。研究從大班秋季學期（上學期）開始，每周干預兩次（周一和周四上午），每次干預時長40分鐘左右。上學期主要進行數數的干預，下學期主要進行數的部分與整體關系的干預。當被試兒童因故沒來幼兒園時，當次干預計劃向后順延一次。上學期實施干預11次，下學期實施干預18次，共計29次，總時長約1160分鐘。具體的干預計劃見表1。

二、干預過程

（一）阿拉伯數字系統

兒童數字系統的學習和發展會經歷兩個階段：初步認識數字階段和完整掌握數字系統階段。第二個階段中，從不完整到完整掌握數字系統的水平又可分為五個層次：（1）“連串”水平，即是對一連串數字的單向整體記憶或背誦，與數數動作無關。（2）“不可斷數鏈”水平，即已能分化辨認出單個數字但無法從一個任意數數起，數物體已成為可能。（3）“可斷數鏈”水平，即已能視數字為既可分割又可相聯的元素，可從任何一個數向前或向后數，說出相鄰數。（4）“數鏈”水平，即數字已被視為可數單位，可用于計數運算或與某個特定數量的集合匹配。（5）“雙向數鏈”水平，即可以熟練地從一個任意數順數或倒數。〔18〕

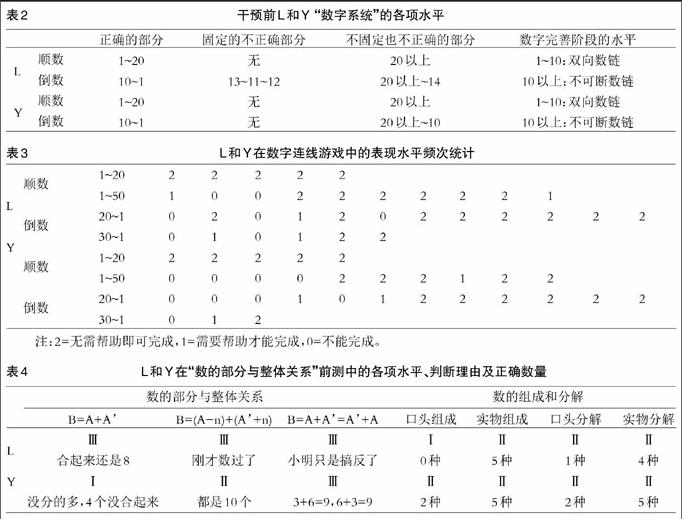
研究發現，兒童所掌握的數字系統往往由三部分組成：（1）正確的數字鏈部分，如1～5。（2）固定的不正確部分，即兒童在多次數數中都重復相同但不正確的數字鏈，尤其是在13～17這一段，有些兒童可能會持續較長時間。（3）不固定也不正確的部分，即每次數到某段數字時都會產生既不同也不正確的數字鏈。〔19〕根據前期觀察診斷，L和Y的數字系統掌握水平詳見表2。

數數的干預主要通過“數字連線”和“數字卡片”游戲進行。L和Y在游戲初期只能從1唱數到20，從10倒數到1。隨著干預次數的增加，L和Y逐漸能夠正確地從1唱數到50，從20倒數到1的正確率也明顯提高。L與Y在“數字連線”游戲中的表現詳見表3。

（二）關于數的部分與整體關系

本研究在開始“數的組成和分解”干預之前，采用林嘉綏設計的“數的部分與整體關系”和“數的組成和分解”測查方案〔20〕考察被試兒童對數的部分與整體概念的理解水平。“數的部分與整體關系”測查主要考察兒童是否理解以下三方面內容：（1）一個總數分為兩個部分數，其總數不變，即B=A+A'。（2）兩個部分數之間存在著互補的關系，即B=（A-n）+（A'+n）。（3）兩個部分數之間存在互換關系，即B=A+A'=A'+A。每項測驗可分為三個操作水平：完全不理解、通過直覺或嘗試錯誤后作出正確判斷、完全掌握。“數的組成和分解”測查分“口頭”和“實物”兩個水平，也可分為三個操作水平：完全不會組成或分解、只會部分組成或分解、完全會組成或分解。L和Y的各項測驗前測水平見表4。

由表4可知，在“數的部分與整體關系”方面，L已能夠完全掌握并說出原因;Y的理解水平較低，后兩項雖然判斷正確，但仍需要借助實物和數字進行推理。在“數的組成和分解”方面，無論是L還是Y，“口頭”水平的正確數量都少于“實物”水平，且在回答過程中隨機性較明顯。

“數的組成和分解”干預分成四個階段：（1）開始時，先進行3次“藏珠子”游戲。把游戲的主動權完全交給兒童，讓他們在游戲中自由探索各種問題解決的方法。（2）隨后，進行3次“小熊捉迷藏”游戲，讓兒童體會“數的分合”，研究者還通過逐一增加“躲進山洞”的小熊數量，讓兒童感受“數的分合”規律。（3）接下來進行5次“小熊請客”游戲，逐步提高難度（從小熊數量和是否允許動手操作兩個方面），引導兒童利用書面符號記錄發現“數的分合”規律（包含關系、互補關系、互換關系），并嘗試運用規律有順序、不遺漏地窮盡某個數字所有的分解與組合方法。（4）最后進行6次“數數棒”游戲，讓兒童通過目測估算，理解并運用“數的分合”知識（如以8號棒為參照，判斷6號棒需要加上幾號棒的長度，才能和8號棒等長）。整個干預過程中，研究者著重引導被試兒童自我建構與體驗，不直接告訴兒童也不急于要求兒童給出答案。具體過程舉例如下。

研究者：今天小熊想邀請5位朋友來家里做客，但家里空間小，一次不能請太多小熊來家里玩，最好分兩次邀請小熊。你能幫我想想有什么好辦法嗎？（研究者通過講故事創設問題情境，同時也以參與者的身份加入到游戲過程中，與L建立起學習共同體。）

L：讓我來想想辦法……可以先邀請3只小熊，再邀請2只小熊（L一邊說一邊把小熊分成相應數量的兩隊）。

研究者：你的方法很棒！幫主人解決了一個大問題。我們把這個好辦法記錄下來吧（引導L在記錄紙上進行記錄）。

（如此循環進行，直至窮盡5的所有分解方法。）

研究者：今天我們幫了小熊一個大忙，想出了很多好辦法。請你看一看記錄紙，自己分析分析，有沒有發現什么規律？（通過啟發提問，引發認知沖突，引導L結合已有記錄進行思考。）

L搖頭表示沒有發現。（此時，研究者并沒有急于告訴L正確答案，而是耐心等待L的頓悟。終于，在幾次游戲之后，L自己報告說：第一次請的小熊多的話，第二次請的小熊就少了，因為沒有那么多小熊了。）

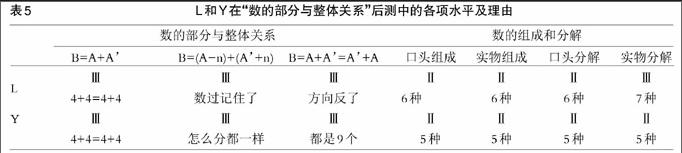
在全部干預結束之后，再次考察被試兒童對“數的部分與整體關系”的理解水平。L和Y各項測驗后測水平見表5，與前測相比進步明顯。

三、干預結果

干預結束時，L與Y已經能夠較為熟練地從1唱數到50、從20倒數到1，“雙向數鏈”水平的數字范圍擴展到1～20;能夠完全理解“數的部分與整體關系”，基本掌握10以內“數的組成與分解”。

在TEMA后測中，L原始分為42分，能力分為115（進步了11分）;Y原始分為42分，能力分為105（進步了16分）。其中，L在干預結束時已接近正常組均分，與正常組均分的差距由21分縮小到5分;Y在干預結束時已接近數困組均分，與正常組均分的差距也由3個標準差縮小到近1個標準差。

四、討論

已有研究總結出兒童對“數的分合”的學習路徑：積累“量的分合”經驗——從“量的分合”到“數的分合”——領會數的分合規律——掌握數的分合關系——用推理的方法學習分合。〔21〕本研究也基本按照這樣的學習路徑開展干預，并證實了干預的有效性。

然而，這樣的學習路徑并不完全適用于數學學習困難兒童。數學學習困難兒童因對“阿拉伯數字系統”的掌握沒有正常兒童熟練，因此必須在進行“數的分解與組合”干預之前幫助他們掌握“數字系統”。研究結果提示，完善“數字系統”——積累“數的分合”經驗——發現“數的分合”規律——運用“數的分合”知識，這樣的干預路徑可能對不同程度數學學習困難兒童均是有效的。

研究發現，兒童理解并記住個位數的加減組合規律，需有一個較長的時間過程。兒童是在理解的基礎上記住這些組合的答案的，一味強調速度、機械背誦會產生不良后果。為兒童創設有目的的練習情境，有利于促進兒童對數的組合知識的掌握。〔22〕本研究在干預過程中，通過游戲創設了真實的問題情境，并且遵循了兒童對“數的部分與整體關系”的理解和掌握規律，耐心等待兒童通過游戲和操作進行自我意義建構，這可能是本研究干預效果較為理想的原因之一。

參考文獻：

〔1〕周欣，趙振國，李娟，等.認知因素對兒童早期數學學習困難的影響〔J〕.學前教育研究，2013，227（11）：3-13.

〔2〕JORDAN N C，GLUTTING J，DYSON N，et al.Building kindergartenersnumber sense：A randomized controlled study〔J〕.Journal of Educational Psychology，2012，104（3）.

〔3〕MORGAN P L，FARKAS G，WU Q.Kindergarten childrens growth trajectories in reading and mathematics：Who falls increasingly behind〔J〕.Journal of Learning Disabilities，2011，44（5）：472-488.

〔4〕JORDAN N C，KAPLAN D，RAMINENI C，et al.Early math matters：Kindergarten number competence and later mathematics outcomes〔J〕.Developmental Psychology，2009，45（3）：850-867.

〔5〕〔10〕GEARY D C，HOARD M K，NUGENT L，et al.Mathematical cognition deficits in children with learning disabilities and persistent low achievement：A five-year prospective study〔J〕.Journal of Educational Psychology，2012，104（1）.

〔6〕李正清，周欣，康丹，等.大班數學學習困難兒童的個案干預研究〔J〕.幼兒教育：教育科學，2013，591/592（7/8）：10-16.

〔7〕GINSBURG H P，BAROODY A J.Test of early mathematics ability〔M〕.Austin：Pro-Ed，2003.

〔8〕康丹，周欣，田麗麗，等.《早期兒童數學能力測試（中文版）》對上海市5～6歲兒童的適用性研究〔J〕.幼兒教育：教育科學，2014，622（6）：39-45.

〔9〕〔12〕〔13〕〔18〕〔19〕〔22〕周欣.兒童數概念的早期發展〔M〕.上海：華東師范大學出版社，2004：2.

〔11〕GEARY D C，BAILEY D H，HOARD M K.Predicting mathematical achievement and mathematical learning disability with a simple screening tool：The number sets test〔J〕.Journal of Psychoeducational Assessment，2009，27（3）：265-279.

〔14〕〔20〕林嘉綏.兒童對部分與整體關系認識發展的實驗研究〔J〕.心理學報，1981，（2）.

〔15〕〔16〕NELSON ?G. Math ?at ?their ?own ?pace：Child-directed activities for developing early number sense〔M〕.St Paul：Redleaf Press，2007.

〔17〕東方沃野.數數棒〔M〕.南昌：江西高校出版社，2010.

〔21〕彭小元.基于幼兒學習路徑重新審視“數的分合”教學〔J〕.幼兒教育，2013，569/570.

A Case Study of Mathematical Game Intervention for 5-6 year-old Children with Mathematical Learning Difficulty

Li Zhengqing1， Zhou Xin2， Tian Lili2， Kang Dan3， Xu Jingjing4

（1University of Denver， Denver， 80208）

（2Faculty of ?Education， East China Normal University， Shanghai， 200062）

（3College of Educational Science， Hunan Normal University， Changsha， 410006）

（4Shanghai Punan Kindergarten， Shanghai， 200120）

【Abstract】This research engaged two 5-6 year-old children with mathematical learning difficulties to explore the effects of mathematical game intervention on number skills of “number words” and “part-whole relationship”. After the intervention， childrens number skills were enhanced more or less. It suggests that the intervention trajectory including perfecting number words， accumulating number experience of separation and reunion， discovering number rule of separation and reunion， applying number knowledge of separation and reunion， might be effective to help MLD childrens understanding of “part-whole relationship”.

【Keywords】children with early mathematical learning difficulties; game intervention; individual case