一種超音速火箭靶彈程序角優化方法研究

沈冠軍, 馮順山, 曹紅松

(1.中北大學 機電工程學院， 山西 太原 030051; 2.北京理工大學 爆炸科學與技術國家重點實驗室， 北京 100081)

?

一種超音速火箭靶彈程序角優化方法研究

沈冠軍1, 馮順山2, 曹紅松1

(1.中北大學 機電工程學院， 山西 太原 030051; 2.北京理工大學 爆炸科學與技術國家重點實驗室， 北京 100081)

針對方案制導超音速火箭靶彈平飛段供靶性能優化問題，提出了一種俯仰程序角優化方法。考慮靶彈彈道始末端點約束及平飛段性能約束，在火箭靶彈縱向飛行平面內建立起俯仰程序角優化設計模型。基于Gauss偽譜法將飛行過程約束轉化成對俯仰程序角的約束，將最優控制問題轉換為對俯仰程序角的非線性規劃問題；利用序列二次規劃算法求解。仿真結果表明，該方法能夠快速獲取最優俯仰程序角，并且具有良好的魯棒性，為實際工程設計提供參考。

兵器科學與技術； 超音速靶彈； 平飛彈道； 程序角優化； Gauss偽譜法

0　引言

超音速靶彈是用于防空武器試驗鑒定及日常訓練時的模擬靶標，常見的研制方式有：利用現役和退役的火箭或導彈改裝；根據供靶指標專門研制新型靶彈。因成本等因素限制，通過對無控火箭彈加裝簡易控制裝置，設計合理的控制程序，使得簡易控制火箭彈能夠模擬飛機、巡航導彈等目標所具有的平飛和俯沖彈道特性，這種設計方式得到了大量應用。文獻[1]提出一種對無控靶彈預置平衡攻角產生升力抵消靶彈重力，并通過陀螺舵等措施防止靶彈旋轉形成平飛來模擬巡航導彈的平飛特性。文獻[2]提出一種對大射程火箭彈改進實現供靶的簡易控制火箭靶彈總體設計方案，通過設計程序俯仰角，在被動段實現有攻角飛行進而實現平飛彈道。

實現平飛或俯沖等彈道特性實質上是對控制變量最優解的求解過程。近年來，運用最優控制理論求解彈道優化問題越來越廣泛。文獻[3]應用極大值原理求解彈道修正引信彈道優化模型，得到了最優法向控制量。文獻[4]針對間接法進行彈道優化時無法獲得全局最優解的缺點，提出了一種改進方法。偽譜法作為直接法的一種，通過離散控制變量和狀態變量將控制問題轉換成為非線性規劃問題，具有設置參數較少，計算精度較高等特點，逐漸成為求解最優控制問題的熱門方法。文獻[5]利用Radau偽譜法將助推- 滑翔飛行器彈道優化問題轉換為非線性規劃問題，得到了最優規避彈道。文獻[6]根據偽譜法將再入動力學微分方程約束轉換成代數方程約束，將制導問題轉換為不需要積分的最優規劃問題。偽譜法種類多，根據配點、節點位置及插值函數的不同而不同，常見用于航空航天領域的有Radau偽譜法、Legendre偽譜法和Gauss偽譜法。Gauss偽譜法在對狀態變量、控制變量和協狀態變量的近似精度以及收斂速度均優于其他兩種偽譜法，同時在對協狀態變量邊界值的估計精度和處理含有初始和終端約束的問題上具有優勢[7]。本文針對超音速靶彈平飛性能優化問題，利用Gauss偽譜法對超音速火箭靶彈程序角進行優化設計，實現靶彈在供靶過程中的最優平飛特性。

1　靶彈供靶彈道方案描述

為模擬超音速飛機與導彈等目標的高空高速特性，需要靶彈能夠在預定的高度穩定地平飛，以提供具備上述目標特性的供靶彈道。常見的靶彈飛行彈道形式如圖1所示。

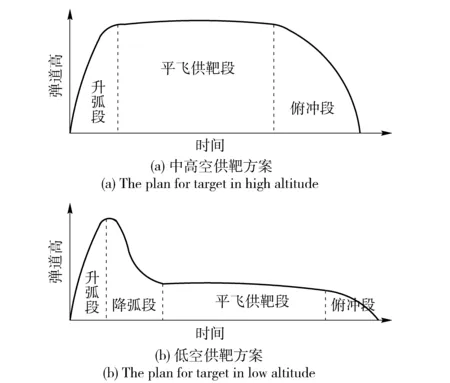
圖1　供靶方案Fig.1　Scheme for target

本文所研究的火箭靶彈是在常規火箭彈的基礎上加裝控制機構改裝而成，執行機構為兩對相互垂直安裝的“十字”鴨舵，采用程序控制與位置修正相結合的方式，通過對程序角的控制，實現預定形式的供靶彈道。靶彈在飛行過程中，通過在穩定尾翼上加裝氣動陀螺舵產生阻止靶彈橫滾的阻尼力矩等方式，改善靶彈整體的橫滾特性，本文假設靶彈發射后在飛行過程中不滾轉。彈載GPS模塊及捷聯慣性測量裝置獲得靶彈某一時刻位置及姿態信息，彈載控制系統計算得到當前彈道與預裝訂的供靶方案彈道之間的偏差量，進而按照既定的控制律經穩定回路計算得出靶彈位置及姿態修正量，并發送給舵機執行，一對方向舵和俯仰舵分別進行靶彈橫向和縱向的偏差修正，從而消除靶彈位置及姿態偏差，控制靶彈按既定的供靶方案彈道穩定飛行，實現平飛、俯沖等運動特性。供靶方案彈道設計的好壞，直接影響靶彈供靶性能及飛行穩定性，因此在設計供靶方案彈道時應盡可能在滿足供靶指標下，設計合適的程序角優化方法，并結合優化方法收斂的有效性和快速性，以尋求最優平飛或俯沖供靶彈道。

傳統的靶彈彈道設計方法是針對彈道不同階段設置不同的俯仰角來實現的。由圖1可將靶彈彈道簡單分為升弧段、平飛段和俯沖段。在升弧段，靶彈按照指定的俯仰角進行爬升。當到達預定平飛高度后在程序俯仰角的作用下，火箭靶彈整體形成正向攻角以產生升力平衡彈體自身重力。由于攻角的存在，靶彈飛行速度不斷減小，故需要不斷改變俯仰角的大小，使得靶彈按照預定的高度進行平飛，當平飛條件結束后，靶彈按照一定的俯仰角俯沖飛行直至落地。經典的程序俯仰角設計滿足如下形式：

(1)

式中：?0、?p分別為靶彈初始俯仰角和平飛時俯仰角；t1、t2為給定指令起控的時間；Kc為控制參數。那么在已知靶彈的飛行參數時，按照經典的程序角形式需對上述5個參數進行設計組合。在諸多的組合方案中存在一組或多組最優解，尋得最優解的過程十分困難與繁雜，同時由于火箭靶彈彈道設計空間高度不連通，往往存在著多個局部最優解。以最優控制的角度來看，實現平飛彈道實質就是求解滿足圖1所示形式的彈道約束的控制變量最優值的求解問題。

2　靶彈動力學模型建立

本文建立的火箭靶彈動力學模型滿足如下基本假設：

1)飛行過程中靶彈側偏為0，忽略火箭靶彈橫向平面運動，只在縱向飛行平面內建立運動模型；

2)彈體無滾轉，整個飛行過程中火箭靶彈只受彈翼整體的阻力、升力，控制舵的阻力、升力，全彈的重力，彈翼整體的穩定力矩、控制舵產生的控制力矩，忽略其他次要力和力矩的影響；

3)控制系統是理想的，能夠對連續信號實時做出響應，即無誤差，無時間延滯，能隨時輸出要求的舵偏角。

在滿足上述假設條件下，在速度系中建立火箭靶彈縱向平面內有控動力學模型：

(2)

式中:m為靶彈質量；A、v、θ、ω、x、y、φ、δ分別為火箭靶彈赤道轉動慣量、速度、彈道傾角、俯仰角速度、射程、射高、俯仰角和攻角；k為誘導阻力系數；α為俯仰舵偏角，即本文所需優化設計的程序角；Cx0、Cx0(α)分別為彈翼整體和舵的零升阻力系數；Cyb′、Cyα′分別為彈翼整體和舵的升力系數導數；m′z、m′zz分別為彈翼整體和舵的俯仰力矩系數導數；Lα為俯仰舵壓心到全彈質心的距離；L為彈長；在計算過程中，零升阻力系數、升力系數導數和俯仰力矩系數導數通過數據表形式插值獲得；ρ為大氣密度，大氣模型參考文獻[8]。

3　最優控制模型建立

靶彈平飛段平飛高度和平飛時間的優化控制，可以選用射程最大化、平飛段射程占總射程比重最大及平飛段高度與預定平飛高度之間的高度差最小化來進行衡量，選取目標函數如(3)式：

(3)

式中：t0、tf分別為彈道發射點和落點時刻；t1、tf1分別為平飛段開始和結束點時刻；k1、k2、k3分別為目標函數中各項所占的權重系數，不同的權重系數取值對優化結果影響很大，應結合不同的工程實際需要設置不同的權重系數，得到適當的優化結果；Rmax為無控火箭彈所能達到的最大射程；Herr為平飛段平飛高度所能允許的波動誤差。通過選取不同的平飛開始時間即可形成如圖1(a)和圖1(b)所示的彈道形式。

靶彈彈道優化過程中滿足如下約束條件：

1)端點約束：以火箭靶彈起始發射點條件為起點約束條件，落點性能條件為終端約束條件。

初始約束：v=v0，θ=θ0，x=x0，y=y0；

終端約束：v=vtf，θ=θtf，x=xtf，y=ytf.

2)過程約束：如(1)式。

3)平飛段約束：簡易控制火箭靶彈平飛段可看作以一定的高度等高飛行，或者飛行過程中彈道傾角θ恒為0°. 在平飛過程中，由于速度不斷地減小，需實時地改變俯仰舵偏角的大小來獲得較大的升力以平衡重力，但是若靶彈嚴格以一定高度平飛，飛行速度在阻力的作用下衰減較快，為平衡重力需增大俯仰舵偏角而產生較大的飛行攻角，使得火箭靶彈的穩定性改變，不利于控制系統的控制，所以本文近似認為平飛段是在滿足一定幅值的平飛高度波動飛行。平飛示意圖如圖2所示。

平飛段滿足約束如下所示：

θpf=0°±θerr,

(4)

Hpf=H0±Herr,

(5)

vmin≤vpf≤vmax,

(6)

式中：θpf、Hpf、vpf分別為平飛時的彈道傾角、平飛高度和平飛速度；θerr為平飛所允許的彈道傾角。

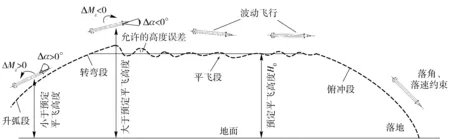
圖2　平飛段供靶彈道Fig.2　The trajectory for target of level flight

4)控制量約束：控制量滿足控制系統所能提供的控制范圍：

|u|≤U，U>0.

(7)

5)為避免俯仰角變換頻率較快，引起靶彈飛行失穩，在飛行中需對俯仰角速度進行約束：

|ω|≤W，W>0.

(8)

4　程序角優化問題求解

4.1運動參數化

第3節中最優程序角的優化設計問題可作為一般最優控制問題：尋找控制變量u(t)∈Rm，最小化具有一般性的Bolza型性能指標：

(9)

式中：狀態變量x(t)∈Rn、初始時間t0和終端時間tf，滿足動力學微分方程約束

(10)

邊界條件

Φ(x(t0),t0,x(tf),tf)=0.

(11)

路徑約束

C(x(t),u(t),t)≤0.

(12)

將(10)式進行泰勒展開，忽略高階項，可得

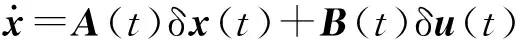
(13)

式中：A(t)=fx(xp,up)，B(t)=fu(xp,up)，xp、up分別為狀態變量和控制變量，結合(2)式火箭靶彈縱向平面內動力學模型，A(t)、B(t)可寫為

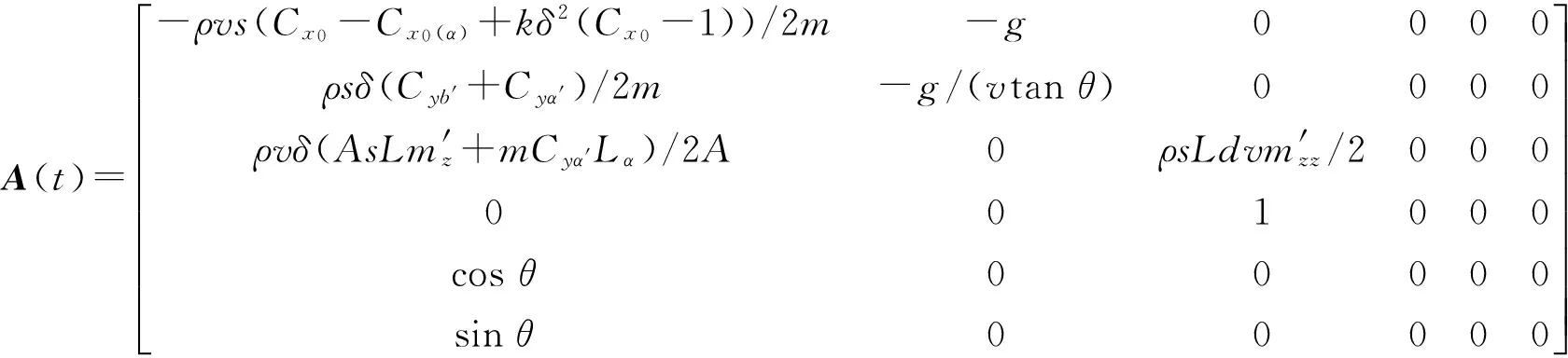
(14)

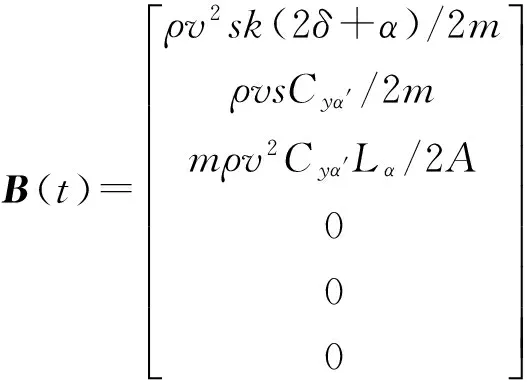
(15)

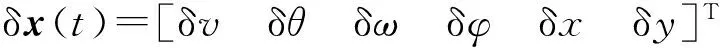
δu)+λT(A(t)δx+B(t)δu),

(16)

式中：λ為協態向量；Q、R為n維半正定矩陣。為使性能函數滿足最優解的1階必要條件，則

(17)

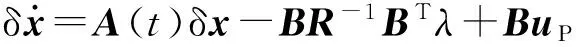
(18)

靶彈彈道優化設計可轉換為兩點邊值問題,

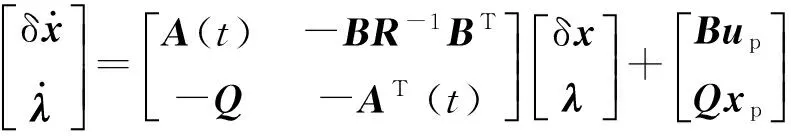
(19)

Gauss偽譜法通過將狀態變量和控制變量在一系列的Gauss點上離散，可將兩點邊值最優控制問題轉換為受一系列代數約束的參數優化問題，其求解步驟：

1)時域變換。設火箭靶彈飛行時間t∈[t0,tf]，將時間離散到τ∈[-1，1]，對時間t變換如下：

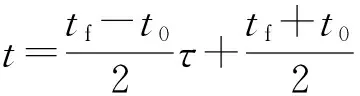
(20)

2)狀態變量與控制變量離散。取K個Legendre-Gauss點為Gauss偽譜法的離散點，即離散點為K階Legendre多項式PK(τ)的根，

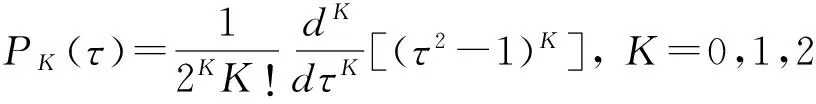
(21)

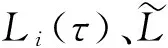
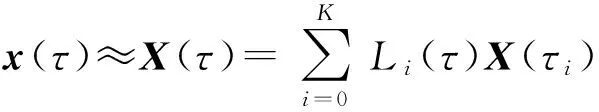
(22)

(23)

4)離散條件下的終端狀態約束。Gauss偽譜法中的節點包括K個配點(τi，…，τk)和初始點τ0≡-1以及終點τf≡1. (22)式未定義終端狀態Xf，終端狀態也應滿足動力學方程約束：

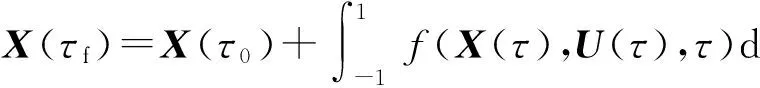
(24)

將終端狀態約束條件離散并用Gauss積分近似:

X(τf)=X(τ0)+

(25)

5)動力學方程約束轉換為代數約束。對(22)式求導可得狀態變量導數，將動力學方程約束轉換為代數約束，即

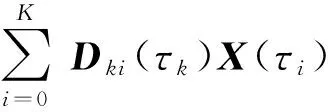
(26)

式中：微分矩陣D∈RK×(K+1)，可離線確定

(27)

式中:τk(k=1，2，…，K)屬于集合κ中的點；τi(i=1，2，…，K)屬于集合κ0={τ0，τ1，…，τk}.

這樣，最優控制問題的動力學微分方程約束即轉換為代數約束:

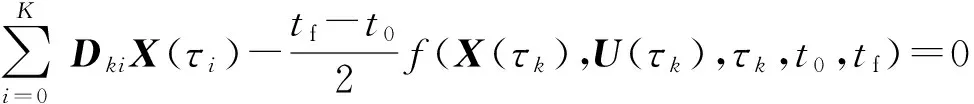
(28)

6)基于Gauss積分的近似性能指標函數。將Bolza型性能指標函數中的積分項用Gauss積分來近似，得到在Gauss偽譜法中的近似性能指標函數：

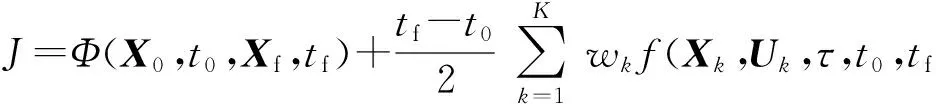
(29)

綜上6個步驟，Gauss偽譜法將連續最優控制問題離散并轉換成為非線性規劃問題。詳細步驟參考文獻[9-13]。

4.2參數化求解

圖3為彈道優化問題的一般流程，通過4.1節將運動方程進行參數化并轉換成一系列非線性規劃方程，利用序列二次規劃法對此非線性規劃方程組進行求解。序列二次規劃法的基本思路為：在每一個迭代步通過求解一個二次規劃子問題來確定一個下降方向，減少價值函數來取得步長，重復這些步驟直到求得問題的解，其基本形式[14]可表示為

圖3　彈道優化流程Fig.3　Optimization process of trajectory

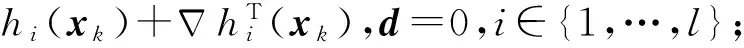
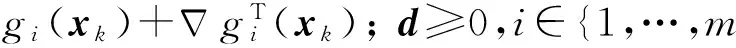
(30)

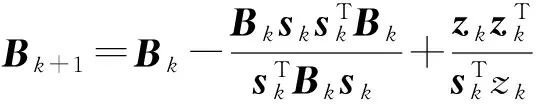
(31)

sk=xk+1-xk,

(32)

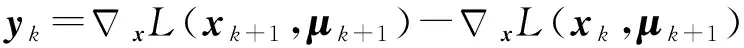
(33)

zk=θkyk+(1-θk)Bksk,

(34)

(35)

5　仿真計算

以某型火箭靶彈的數據為例，將火箭靶彈主動段末速度等效為炮口速度，質量m0=800 kg，出炮口速度v0=1 650 m/s，起始射角35°，氣動數據通過氣動軟件計算獲得，飛行最大允許攻角δ<5°，舵偏角|α|≤20°，平飛高度10 km，允許上下浮動100 m，平飛彈道傾角允許上下浮動5°，落角θf≥30°，超音速指標滿足飛行速度v≥400 m/s，終端時間自由。

利用上述偽譜法原理，將方程組參數化，編制程序，選取插值點數為160，權重系數k1=10，k2=k3=1，在計算機內存為8 G，主頻為2.66 GHz四核環境下，計算耗時10.289 491 s. 表1和圖4為相同初始條件下無控彈道和最優程序角作用下的彈道參數對比。

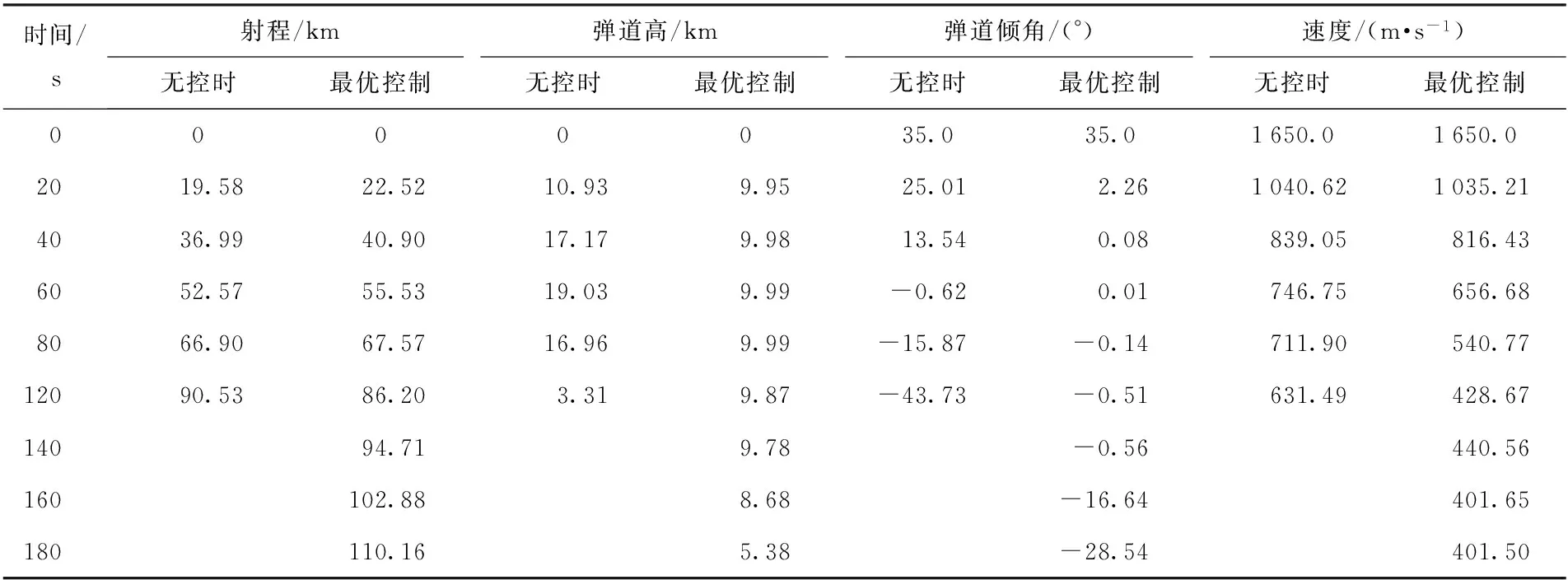
表1　控制前后彈道參數對比

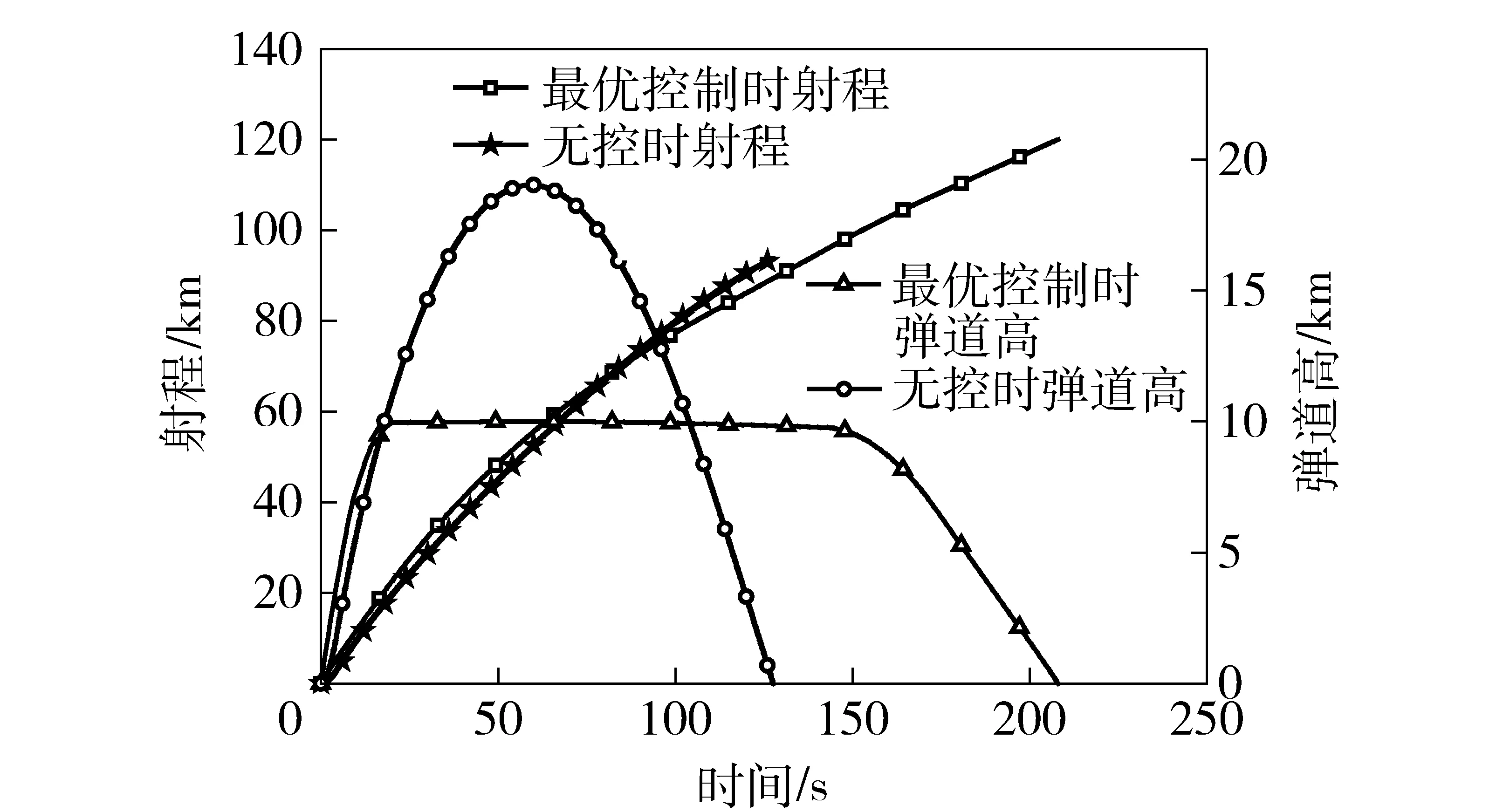
圖4　控制前后射程和彈道高對比Fig.4　Comparison of height and range

從圖4和表1中數據可以看出，在優化設計后的俯仰舵偏角的作用下，射程和滯空時間相比無控彈道明顯增加，彈道高按照預定的高度相比無控彈道更為平直，無控拋物線彈道特性明顯被改善。

圖5所示為優化設計后的俯仰舵偏角曲線和攻角曲線。結合圖4、圖5可知，在彈道上升段，火箭靶彈在一個大的負舵偏角下飛行，其目的是使靶彈整體形成一個負攻角產生向下的升力，將彈道在預定的平飛高度盡早拉平。當火箭靶彈進入平飛階段后，隨著速度的減小，俯仰舵以正的舵偏角產生向上的升力抵消重力實現平飛。平飛階段結束后，俯仰舵在圖5舵偏角規律下滿足落點速度和落角大小的約束飛行。整個飛行過程中產生的攻角絕對值小于2°，滿足飛行穩定性的要求。

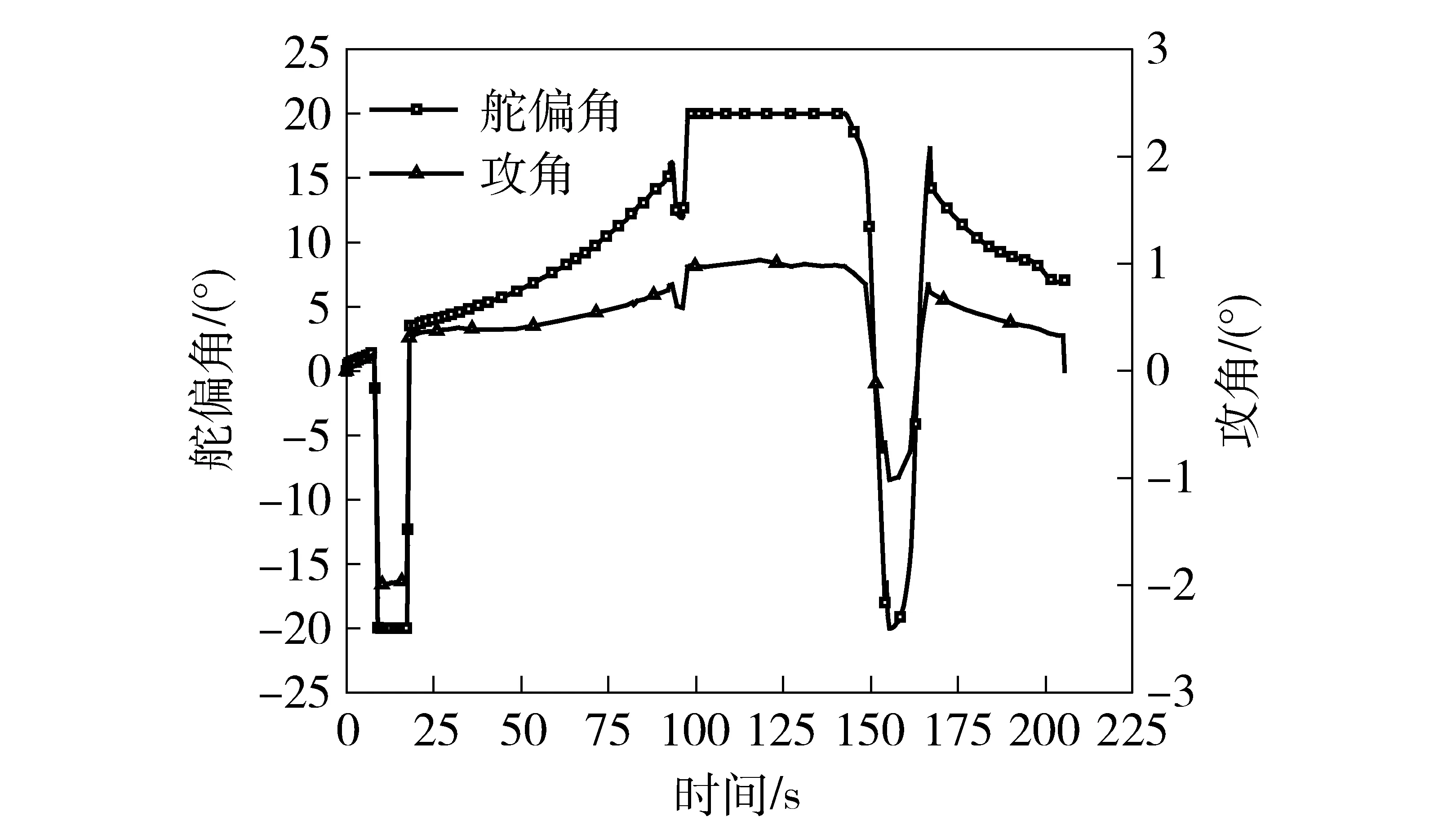
圖5　舵偏角和攻角曲線Fig.5　Rudder angle and attack angle curves

圖6、圖7為相同起始條件、飛行約束條件及落點約束條件下，采用本文方法與經典俯仰程序角設計方法所優化得到的彈道結果對比曲線。由圖6、圖7可知，本文方法優化所得平飛段平飛高度、彈道傾角基本維持在10 km和0°，滿足平飛約束條件。落角和落點速度為30°、400 m/s滿足落點約束條件。相比經典設計方法，采用本文方法的火箭靶彈供靶彈道更為平直；在滿足供靶指標的前提下，其供靶時間136.8 s，也較經典設計方法下87.7 s更長，具有更好的平飛供靶性能。同時，在起始條件、終端約束及飛行指標相同的條件下，本文所述方法僅選取俯仰舵偏角為優化變量，參數設置簡單，計算效率高，而經典俯仰程序角設計方法則需對(1)式中5個參數變量組合進行尋優，計算效率明顯降低，計算結果是否收斂于最優解難以得到保證。

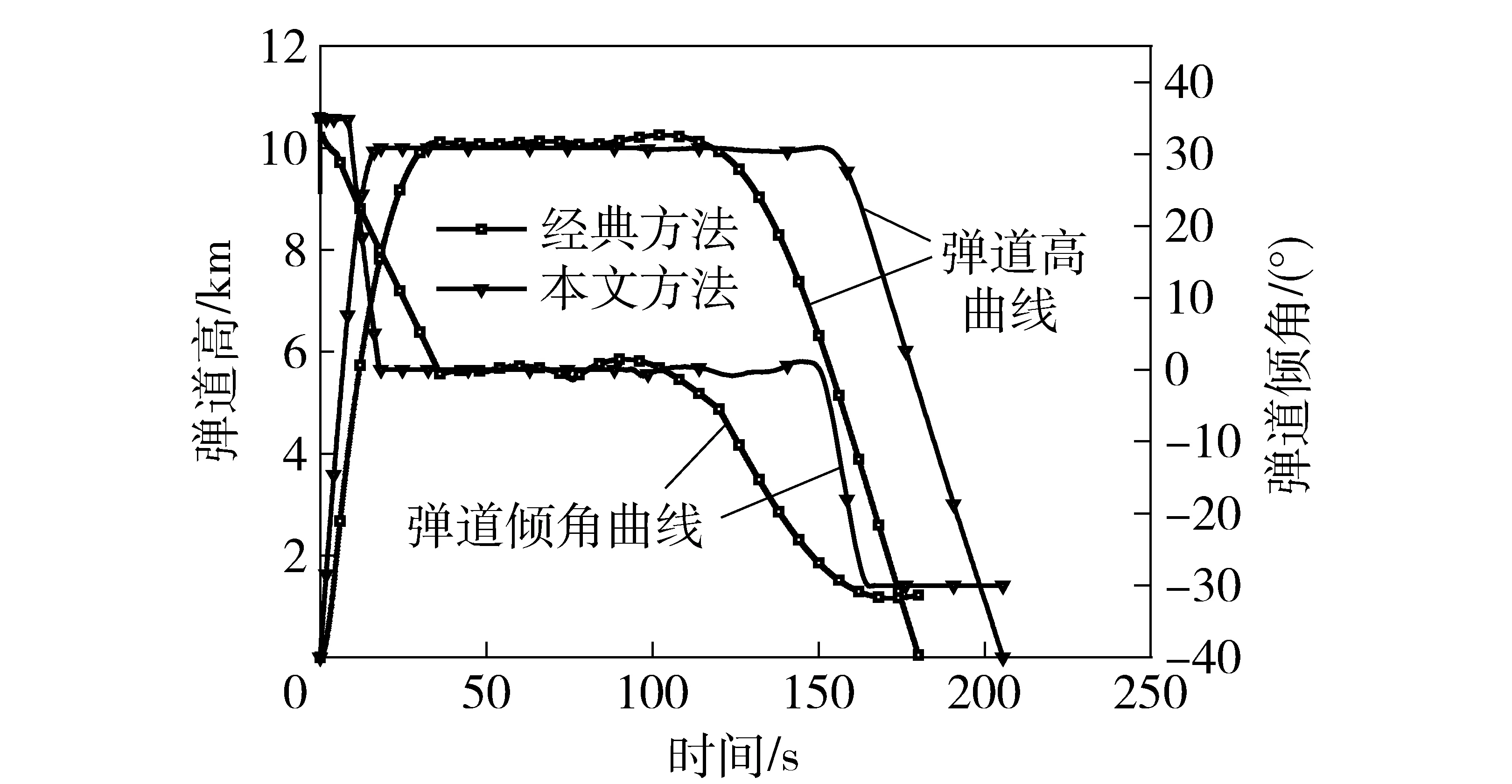
圖6　彈道高和彈道傾角曲線Fig.6　Height and trajectory obliquity curves

圖7　彈道高和速度曲線Fig.7　Height and velocity curves

為驗證本文方法的魯棒性，在火箭靶彈質量、炮口條件、飛行約束條件及目標函數相同的情況下，研究參數不確定性對系統控制量變化規律及最優彈道的影響，圖8、圖9為不同射角下俯仰舵偏角變化曲線和彈道高曲線。

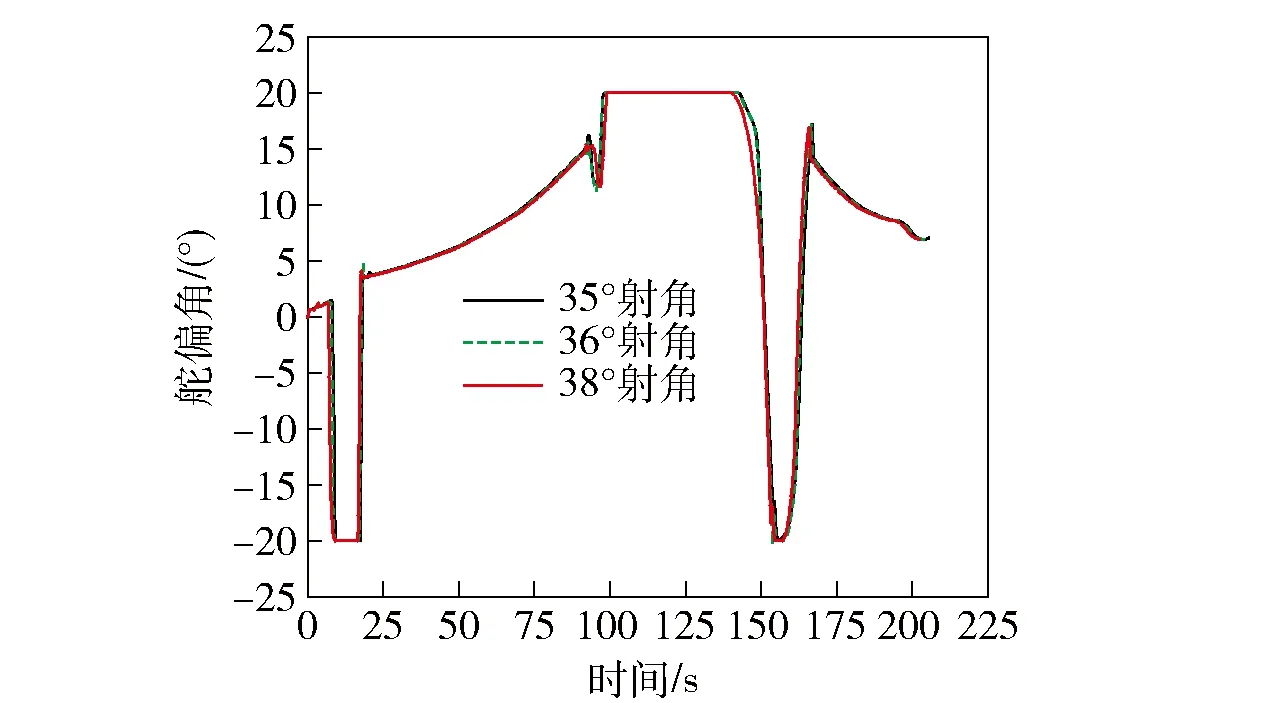
圖8　不同射角下舵偏角變化曲線Fig.8　Rudder angle curves at different fire angles

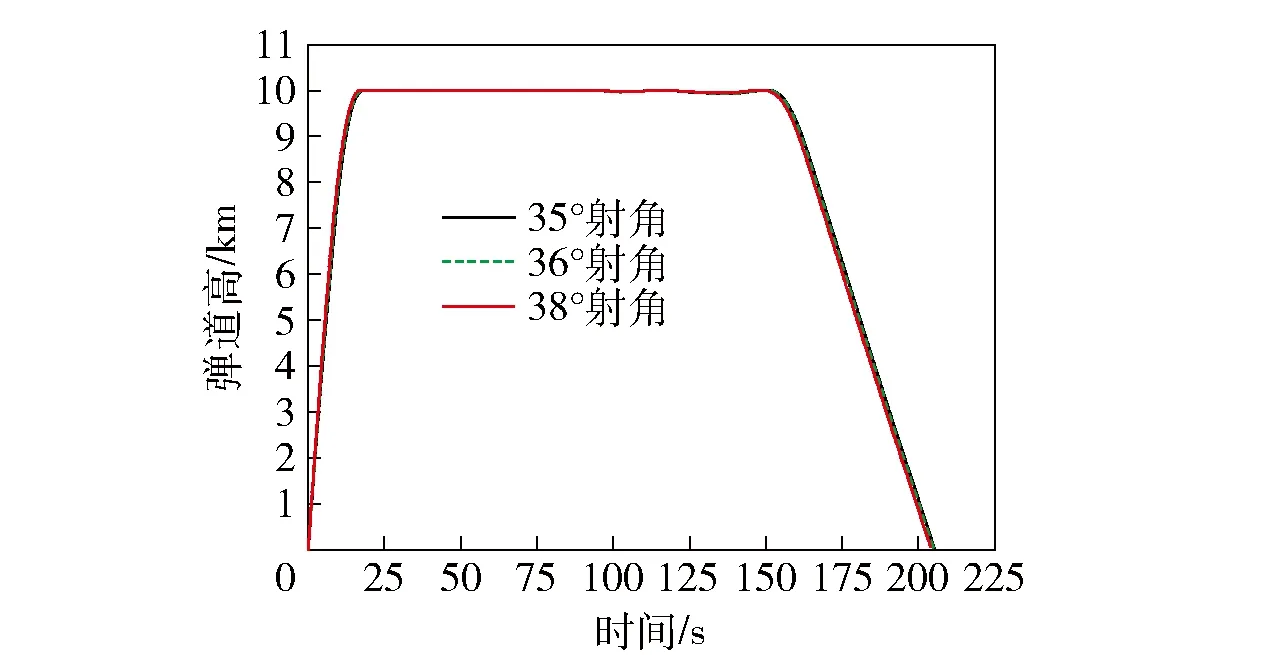
圖9　不同射角下彈道高曲線Fig.9　Height curves at different fire angles

任取射角為35°時優化得到的舵偏角曲線和彈道高曲線，并以此舵偏角曲線作為初始射角為36°時的控制曲線，計算得到兩種不同起始射角下的彈道高誤差曲線，如圖10所示。

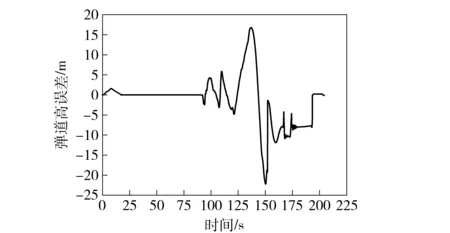
圖10　彈道高誤差曲線Fig.10　Height error curve

由圖8和圖9可以看出，在不同的射角下，其舵偏角變化規律和彈道高曲線分別基本一致。圖10表明，利用Gauss偽譜法獲得的俯仰舵偏角變化規律用于起始射角變化后所得的彈道高曲線仍滿足供靶指標要求，這是因為Gauss偽譜法是一種采用全局配點的優化方法，可以很好地避免了模型等參數不確定性的干擾，具有良好的魯棒性。

圖11是在改變起始發射角及調整平飛段起控時間后，利用本文方法所獲得如圖1(b)所示的低空供靶彈道，包含彈道高、速度與彈道傾角變化曲線。對比圖6所示彈道，圖11所示的平飛供靶時間明顯小于圖6所示彈道的平飛供靶時間，但是在滿足速度指標下，圖11所示彈道在過彈道頂點后至平飛供靶開始之間，可模擬目標的俯沖特性，從而實現一靶多用。

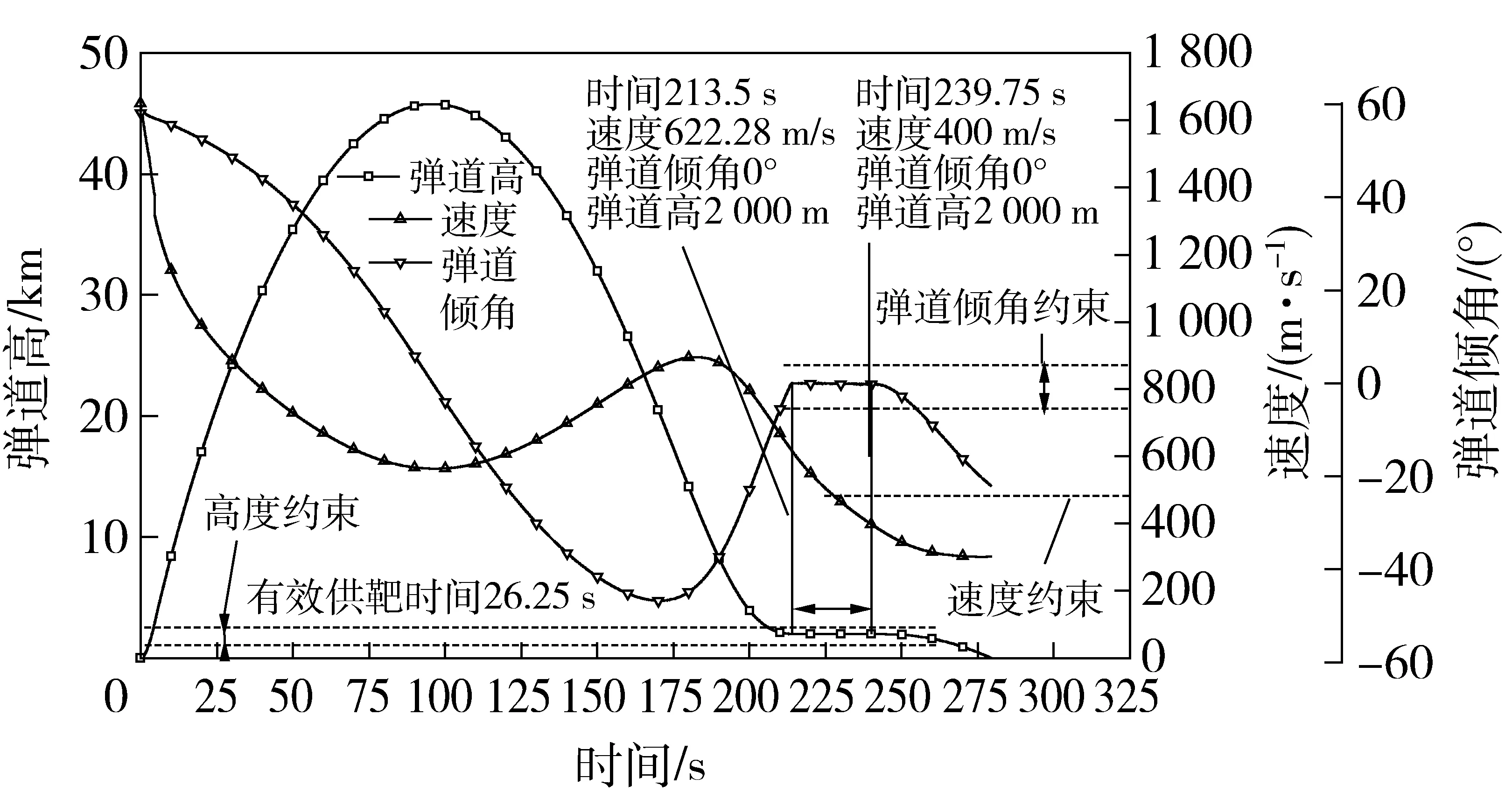
圖11　低空平飛供靶彈道Fig.11　Level flight trajectory for target at low-altitude

為簡化火箭靶彈升弧段俯仰舵偏角設計，通過采用使靶彈升弧段任意時刻滿足升阻比最大，并以平飛滑翔開始時飛行動能最大為優化目標的優化策略，利用成熟的優化方法優化獲得火箭靶彈最優射角和升弧段起控時間，進而以此射角和起控時間為初始條件，采用本文方法對俯仰舵偏角進行優化，快速獲得滿足供靶指標的供靶彈道。因高空舵控效率降低，平飛供靶性能可允許在供靶階段內具有一定的彈道落差，實現準平飛供靶。采用上述火箭靶彈數據，在15 km高空優化火箭靶彈準平飛供靶彈道，高空供靶落差不大于2 km，其他約束條件及供靶性能指標同上。采用粒子群算法優化在射角范圍θ0∈[30°,60°]，升弧段起控時刻tc∈[5 s,8 s]，優化獲得起始射角和起控時間分別為50.56°，8 s. 以此為初始計算條件，采用本文俯仰舵偏角優化方法，優化獲得15 km高空下準平飛供靶彈道如圖12所示，供靶過程優化耗時13.58 s.

圖12顯示，利用本文提出的方法，能夠在高度為15 km下快速優化出滿足供靶指標的供靶彈道，供靶時間為122.81 s，同時滿足落點性能約束。

圖12　高空準平飛供靶彈道Fig.12　Level flight trajectory at high-altitude

6　結論

針對超音速靶彈平飛段平飛性能問題，分析了超音速靶彈平飛段的相關約束，建立了火箭靶彈程序角設計模型，通過Gauss偽譜法將此最優控制問題轉換成一系列非線性規劃問題。以最大射程、平飛段射程所占總射程的比重及平飛段飛行高度和指定平飛高度差最小為目標，利用序列二次規劃法求解得到了實現靶彈平飛的最優程序角變化規律及最優方案供靶彈道，系統具有良好的魯棒性、相比經典俯仰程序角設計方法具有設置參數與優化變量少，計算時間短等特點，能夠為簡易控制超音速靶彈平飛供靶方案制導設計提供相關的參考。

References)

[1]張邦楚, 韓子鵬, 范雁飛. 巡航導彈模擬靶平飛彈道設計[J].彈道學報, 2003, 15(2): 28-33.

ZHANG Bang-chu, HAN Zi-peng, FAN Yan-fei. Design of the level trajectory of cruise missile simulated target [J]. Journal of Ballistics, 2003, 15(2):28-33. (in Chinese)

[2]李曉斌, 王永杰, 孫曉峰. 簡易控制火箭靶彈總體設計[J]. 彈道學報, 2010, 22(1): 41-44.

LI Xiao-bin, WANG Yong-jie, SUN Xiao-feng.System design of simple control rocket target[J]. Journal of Ballistics, 2010, 22(1):41-44. (in Chinese)

[3]霍鵬飛, 施坤林, 苑偉政. 基于極大值原理的彈道修正引信彈道優化控制研究[J]. 兵工學報, 2007, 27(3): 301-304.

HUO Peng-fei, SHI Kun-lin, YUAN Wei-zheng. Research on trajectory controlled optimization for trajectory correction fuze using maximum principle[J]. Acta Armamentarii, 2007, 27(3): 301-304. (in Chinese)

[4]李永遠, 姜毅, 高偉濤, 等. 間接法求解具有最大橫程的再入軌跡[J]. 北京理工大學學報, 2013, 33(7): 665-668.

LI Yong-yuan, JIANG Yi, GAO Wei-tao, et al. Indirect method for solving the reentry trajectory with maximum cross range[J]. Transactions of Beijing Institute of Technology, 2013, 33(7):665-668. (in Chinese)

[5]李柯, 聶萬勝, 馮必鳴. 助推- 滑翔飛行器規避能力研究[J]. 飛行力學, 2013, 31(2): 148-156.

LI Ke, NIE Wan-sheng, FENG Bi-ming. Research on elusion capability of boost-glide vehicle[J]. Flight Dynamics, 2013, 31(2): 148-156. (in Chinese)

[6]水尊師, 周軍, 葛致磊. 基于高斯偽譜方法的再入飛行器預測校正制導方法研究[J]. 宇航學報, 2011, 32(6): 1249-1254.

SHUI Zun-shi, ZHOU Jun, GE Zhi-lei. On-line predictor-corrector reentry guidance law based on Gauss pseudospectral method[J]. Journal of Astronautics, 2011, 32(6): 1249-1254. (in Chinese)

[7]Huntington G T. Advancement and analysis of a Gauss pseudospectral transcription for optimal control problems[D]. MA: Massachusetts Institute of Technology, 2007: 23-49.

[8]林獻武. 高空環境下彈箭的彈道特性研究[D].南京: 南京理工大學, 2009: 9-13.

LIN Xian-wu. A research on the ballistic characteristics of projectile flying at high altitude environment[D].Nanjing: Nanjing University of Science and Technology, 2009: 9-13. (in Chinese)

[9]Garg D, Hager W W, Rao A V. Pseudospectral methods for solving infinite-horizon optimal control problems[J].Automatica, 2011, 47(4): 829-837.

[10]Maleki M, Hashim I. Adaptive pseudospectral methods for solving constrained linear and nonlinear time-delay optimal control problems [J].Journal of the Franklin Institute, 2014, 351(2): 811-839.

[11]Rao A V, Clarke K A. Performance optimization of a maneuvering re-entry vehicle using a legendre pseudospectral method[C]∥2002 AIAA Atmospheric Flight Mechanics Conference. Monterey, US: American Institute of Aeronautics and Astronautics, 2002.

[12]Rao A V, Benson D A, Darby C. Algorithm 902: GPOPS, A MATLAB software for solving multiple-phase optimal control problems using the gauss pseudospectral method[J].ACM Transactions on Mathematical Software, 2010, 37(2): 1-39.

[13]Garg D, Rao A V, Hager W W. Gauss pseudospectral method for solving infinite-horizon optimal control problems[C]∥AIAA Guidance, Navigation, and Control Conference.Toronto, Ontario, Canada Toronto: American Institute of Aeronautics and Astronautics, 2010: 1-9.

[14]鄭總準, 吳浩, 王永驥. 基于序列二次規劃算法的再入軌跡優化研究[J]. 航天控制, 2009, 27(6): 8-13.

ZHENG Zong-zhun, WU Hao, WANG Yong-ji.Reentry trajectory optimization using sequential quadratic programming[J]. Aerospace Control, 2009, 27(6): 8-13. (in Chinese)

Research on a Program Angle Optimization Method for Supersonic Rocket Target

SHEN Guan-jun1, FENG Shun-shan2, CAO Hong-song1

(1.School of Mechatronics Engineering, North University of China, Taiyuan 030051, Shanxi, China; 2.State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China)

An optimization method of pitch program angle is proposed for the optimization problems of level flight trajectory of supersonic rocket target. Considering the initiation and impact point of rocket target and the level flight state constraints, the pitch program angle optimization model is built on the longitudinal flight plane of rocket target. The Process constraints are transformed to the pitch program angle constraints, and the optimal control problems are translated to the nonlinear programming problems based on Gauss pseudo spectral method. And then the nonlinear programming problems are solved by sequential quadratic programming method. Simulation results show that this proposed method can quickly obtain the optimal program pitch angle, and has good robustness.

ordnance science and technology; supersonic rocket target； level flight trajectory； program angle optimization； Gauss pseudo spectral method

2014-05-06

兵器“十二五”預先研究支撐基金項目(62201070503)

沈冠軍(1987—)，男，博士研究生。E-mail:mmlife@126.com;

馮順山(1952—)，男，教授，博士生導師。E-mail:ssfeng@bit.edu.cn

TJ013.2

A

1000-1093(2015)04-0644-09

10.3969/j.issn.1000-1093.2015.04.011