一種電子倍增CCD電子倍增增益的確定方法

盧家莉， 李彬華， 胡泊

(昆明理工大學 信息工程與自動化學院， 云南 昆明 650500)

?

一種電子倍增CCD電子倍增增益的確定方法

盧家莉， 李彬華， 胡泊

(昆明理工大學 信息工程與自動化學院， 云南 昆明 650500)

電子倍增電荷耦合器件(EMCCD)相機在使用過程中，需要校正其電子倍增增益。根據(jù)EMCCD的結(jié)構(gòu)特征和單級倍增寄存器的電荷倍增特性，分析了已有電子倍增模型在實際應(yīng)用中的局限性。針對特定的EMCCD器件，通過仿真計算，得到原有增益計算模型的關(guān)鍵參數(shù)與EMCCD工作電壓、溫度的數(shù)據(jù)表，并用多元回歸分析的方法建立該參數(shù)與工作電壓、溫度的數(shù)學方程，利用該方程，代入原有增益計算模型，可以突破原增益計算模型的限制，得到了一種普遍適用且較為簡單的EMCCD電子倍增增益計算方法。仿真計算所得結(jié)果與實際EMCCD器件的倍增曲線比較，數(shù)據(jù)吻合良好。該結(jié)果表明，這種確定增益的方法可以較方便地計算電子倍增器件的平均增益，在EMCCD相機設(shè)計和實際使用中有著良好的應(yīng)用價值。

光電子學與激光技術(shù)； 電子倍增電荷耦合器件； 電子倍增增益； 參數(shù)計算； 仿真分析

0　引言

電子倍增電荷耦合器件(EMCCD)是微光成像領(lǐng)域的重大突破，它是在普通的CCD基礎(chǔ)上嵌入可控的增益寄存器，使信號電荷在水平轉(zhuǎn)移的過程中得到放大倍增，從而可以有效降低信號的讀出噪聲，特別適合于微光成像系統(tǒng)中[1]。

EMCCD成像系統(tǒng)的電子倍增增益值過低或是增益值過高，系統(tǒng)的成像質(zhì)量均會下降[2]。因此，用戶在使用EMCCD相機的過程中，了解電子倍增增益是一個重要的問題。由于EMCCD在使用過程中，電子倍增增益會發(fā)生變化[3]，這種變化可以通過專門的EMCCD測試平臺去獲得，但普通用戶無法進行這樣的測試。因此，有必要研究一種簡易的確定EMCCD電子倍增增益的方法。

由于EMCCD的電子倍增機制是電子信號在EMCCD轉(zhuǎn)移的過程中發(fā)生碰撞電離，所以，國內(nèi)外大多數(shù)的學者在研究EMCCD電子倍增模型時，首先討論EMCCD的電離率模型，再討論EMCCD電子倍增模型[4-6]。這樣的研究方法是可行的，但不實用，特別是對于使用過一段時間的EMCCD相機，因為其內(nèi)部偏置電壓的變化和倍增寄存器的老化等因素，電子倍增增益必然會發(fā)生變化。因此，EMCCD的生產(chǎn)商英國e2v公司的研究人員提出了一種比較簡單的EMCCD倍增增益的確定方法[7]，其思想是根據(jù)EMCCD的電子倍增寄存器的輸入輸出信號確定電子倍增器件的倍增增益。該方法對于e2v公司生產(chǎn)的模型參數(shù)已知的EMCCD器件是適用的。對于EMCCD的另一供應(yīng)商美國TI公司生產(chǎn)的EMCCD器件，由于模型參數(shù)是未知的，該方法就不適用了。

本文在e2v公司方法的基礎(chǔ)上，通過對TI公司生產(chǎn)的EMCCD器件TC285和TC253電子倍增過程的分析，分別確定了這兩種倍增器件使用e2v的模型時的參數(shù)，從而建立相應(yīng)的電子倍增增益模型。這種確定EMCCD電子倍增模型參數(shù)的方法，可以很容易地推廣用于其他一些用戶不知道該參數(shù)的EMCCD相機之中，通過確定其模型參數(shù)，進而可以用e2v的模型來確定相機所用EMCCD器件在當前情況下的電子倍增增益。

1　EMCCD及其電子倍增增益

EMCCD器件的兩個生產(chǎn)廠商英國的e2v公司和美國的TI公司，他們生產(chǎn)的EMCCD基本結(jié)構(gòu)和傳統(tǒng)的幀轉(zhuǎn)移CCD結(jié)構(gòu)大致相同，主要包括成像區(qū)、存儲區(qū)和讀出放大器三部分。不同的是，EMCCD在移位寄存器末端和讀出放大器之間插入了一個信號電荷載流子倍增寄存器(CCM)，使得信號電荷在水平轉(zhuǎn)移過程中實現(xiàn)片上倍增。

圖1為電子在單個倍增寄存器內(nèi)轉(zhuǎn)移和倍增的示意圖。Φ1、Φ3、ΦDC、Φ2HV為倍增寄存器的時鐘電極，其中：Φ1和Φ3為普通的轉(zhuǎn)移時鐘電極；ΦDC為直流偏置電極，保持固定電勢，典型值1.5 V；Φ2HV為電荷倍增柵極(CMG)，該電極加有高壓時鐘脈沖，幅值比普通的轉(zhuǎn)移時鐘電極大許多。當Φ1電極的電壓變低，Φ2HV電極的電壓變高時，電子從Φ1電極區(qū)轉(zhuǎn)移到Φ2HV電極區(qū)，電子在轉(zhuǎn)移的過程中被加速，部分電子發(fā)生碰撞電離，使電子的數(shù)目增加。

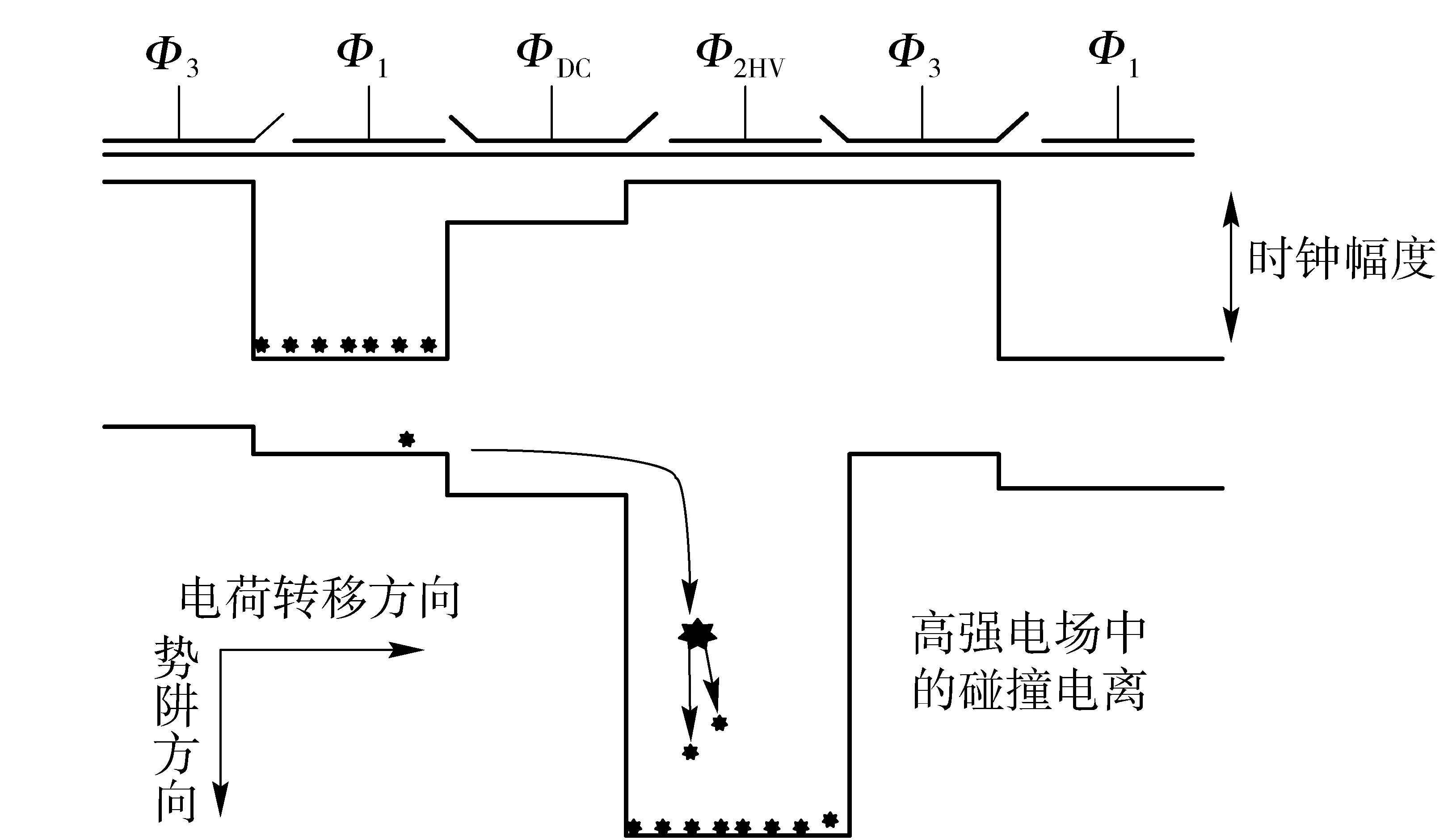
圖1　EMCCD單級倍增寄存器示意圖Fig.1　Single multiplication element of EMCCD

對于單級倍增區(qū)域，單級倍增寄存器的增益g=1+r，r是單級倍增寄存器放大信號電荷倍增率，雖然單級的增益非常小，但是經(jīng)過多級N倍增后的總平均增益G與單級增益g呈指數(shù)關(guān)系，即可實現(xiàn)高倍的電子倍增增益，最終總平均增益G很大，其計算公式：

G(r)=(1+r)N.

(1)

以TI公司出產(chǎn)的TC285芯片為例，其倍增寄存器有400級，單級倍增率r的典型值為0.01. 那么G(0.010)=54，而G(0.013)=175. 如圖1所示，通過調(diào)節(jié)倍增寄存器上高壓倍增電極Φ2HV的電壓值，從而可以調(diào)節(jié)單級電荷倍增率r的大小，進而調(diào)節(jié)總平均倍增增益G(r).

2　EMCCD電子倍增模型

國內(nèi)外很多學者對不同條件下EMCCD的電子倍增特性做了比較深入的研究。張燦林等使用Wolff碰撞電離模型[8]和Grant提供的參數(shù)建立了EMCCD電子倍增數(shù)學模型[5]，該模型能夠在常溫下對倍增器件的總增益隨CMG電壓變化進行較為準確的預測。胡泊等基于Valdinoci等提出的電離率模型[9]建立了低溫下EMCCD電子倍增模型[4]，該模型可以在低溫條件下準確預測EMCCD的級聯(lián)總增益隨CMG電壓的變化。這些電子倍增CCD增益模型都是建立在碰撞電離率基礎(chǔ)之上，對于具有專門知識的研究人員可以方便地使用，但對于EMCCD相機的一般用戶而言，他們對EMCCD的內(nèi)部倍增機理了解不多，使用這些電子倍增模型就有一定的困難。對于這種情況可以根據(jù)倍增寄存器的輸入輸出信號，采用Robbins提出的倍增增益模型[7]，通過分析計算確定模型中待定參數(shù)值，建立電子倍增增益模型。

EMCCD倍增寄存器的平均增益與高壓倍增時鐘、工作溫度以及EMCCD的老化時間3個因素有關(guān)[10]，其單級倍增率r：

r=X(T)Y(V)Z(t)，

(2)

式中：X(T)是工作溫度T的函數(shù)；Y(V)是電勢差V的函數(shù)；Z(t)是關(guān)于EMCCD老化時間t的函數(shù)。該關(guān)系式中，溫度T和電勢差V互不相關(guān)，Y(V)可以用(3)式表示：

Y(V)∝exp(cV)，

(3)

式中：V為Φ2HV與ΦDC兩極之間的電勢差；c是待定參數(shù)。將(3)式代入(2)式后再代入(1)式，EMCCD倍增寄存器總的平均增益可寫成：

G≈(1+βexp (cV))N，

(4)

式中：β是與電勢差V無關(guān)但與溫度T和老化時間t有關(guān)的變量。當EMCCD的級聯(lián)總增益≤5 000且倍增級數(shù)≥400[7]時，(4)式可簡化為

G≈exp (Nβexp (cV)).

(5)

若已知高壓倍增時鐘電極Φ2HV的高電平電壓值，則可以測量出倍增寄存器的平均增益G.Si是倍增寄存器的輸入信號，S1是倍增寄存器的平均輸出信號，V1是高壓倍增電極Φ2HV和直流偏置電極ΦDC的電勢差。EMCCD倍增寄存器的平均輸出信號S1如下：

S1=G1Si=Siexp (Nβexp (cV1)).

(6)

G1是待測增益，在溫度T不變的條件下，把高壓電極Φ2HV和直流電極ΦDC的電勢差設(shè)為V2，使得EMCCD倍增增益發(fā)生變化，從而引起平均輸出信號S2的改變。平均輸出信號S2由(7)式表示：

S2=Sinexp (Nβexp (cV2)).

(7)

結(jié)合(6)式和(7)式，可以求出待測增益G1：

(8)

從(8)式可以看出，倍增寄存器的平均增益G1只與高壓倍增電極Φ2HV和ΦDC的電勢差V1、V2，倍增寄存器的平均輸出信號S1、S2，待定參數(shù)c有關(guān)，而與EMCCD的工作溫度T和老化時間t沒有關(guān)系。

(8)式即為e2v公司的EMCCD電子倍增增益模型。如果已知參數(shù)c，就可以通過兩次測試計算出當前EMCCD的電子倍增增益。EMCCD倍增器件的型號不同，參數(shù)c值也不同。所以，對于不知道該參數(shù)c的用戶來說，就難以使用該模型確定EMCCD的電子倍增增益。事實上，EMCCD的另一生產(chǎn)商TI公司并沒有告知用戶其EMCCD器件使用增益計算模型(8)式的參數(shù)c，因此，對于這一大類器件以及相關(guān)的相機，有必要研究并導出不同EMCCD器件的參數(shù)c的確定方法。

3　TI公司的EMCCD器件參數(shù)c的確定方法

TI公司出品的TC253和TC285芯片是倍增級數(shù)均為400的幀轉(zhuǎn)移EMCCD電子倍增器件，本文以這兩種器件為例，介紹參數(shù)c的確定方法。

首先假定EMCCD的工作溫度T變化不大，并已知高壓倍增電極Φ2HV與ΦDC電勢差為V1和V2時對應(yīng)的平均輸出信號為S1和S2. 這時，參數(shù)c可以通過以下方法確定：設(shè)與V1和V2對應(yīng)的EMCCD的平均增益分別是G1、G2，倍增寄存器的輸入信號設(shè)為Si，由增益計算公式(8)迭代可計算出c值。參數(shù)c可由(9)式表示：

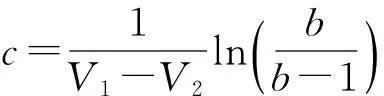
(9)

式中：b=lnG1/ln(S1/S2).

根據(jù)TI公司提供的TC285數(shù)據(jù)手冊[11]，借助MATLAB分別計算器件溫度T分別為-25 ℃、-15 ℃、0 ℃、15 ℃、25 ℃這5種情況下的c值。對于該器件來說，高壓倍增電極Φ2HV連接的是驅(qū)動時鐘CMG，而ΦDC連接的是直流偏置電壓FP. 因此，在計算過程中，Vi=CMGi-FP，i=1，2，其中，CMG1是TC285手冊中不同的驅(qū)動時鐘的高電平值，F(xiàn)P為1.5 V. 由該器件數(shù)據(jù)手冊可知，當CMG電壓小于18.5 V時，EMCCD電荷倍增增益在這5組溫度下均接近1. 為了便于計算分析，CMG2取固定值10.5 V，則V2=9 V. 對應(yīng)于上述5種溫度條件，V1取多個不同的電勢差時計算的參數(shù)c值見表1所示。

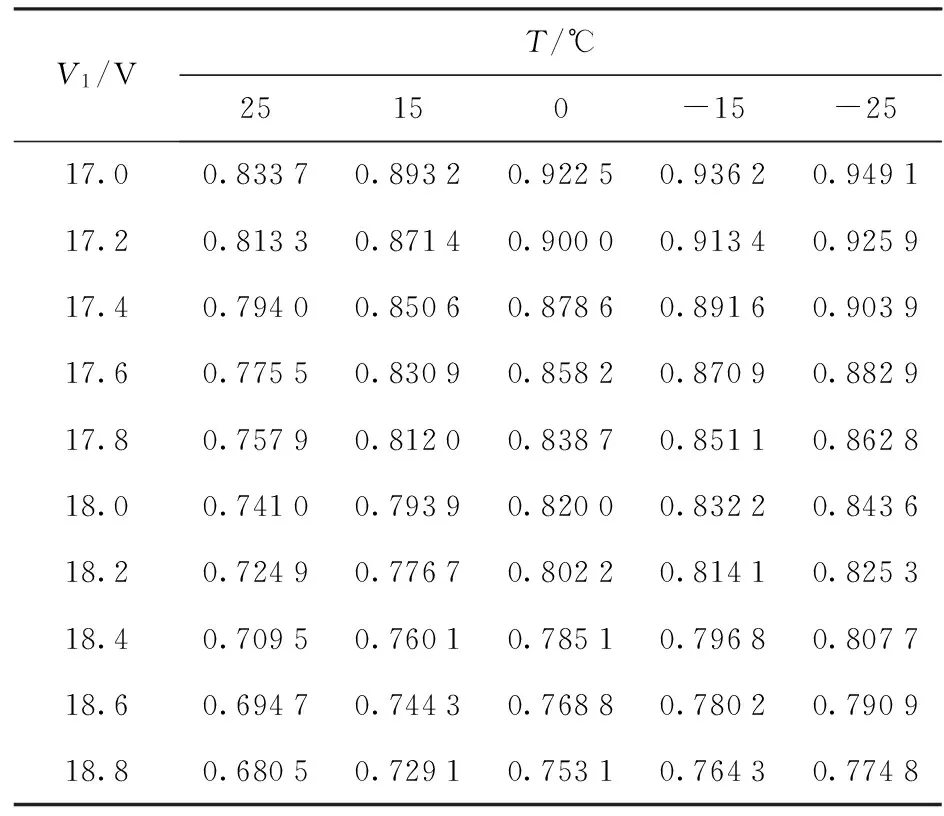
表1　TC285的參數(shù)c值

從表1可以明顯看出，隨著電壓的增大，c值逐漸下降；隨著溫度的下降，c值逐漸增大。說明模型中的參數(shù)c確實能夠反映EMCCD相機內(nèi)部偏置電壓、芯片工作溫度等因素的影響。為了進一步描述待定參數(shù)c值，用多元回歸分析的方法建立參數(shù)c的數(shù)學模型。在表1所示的溫度T和電勢差V1電壓范圍內(nèi)，利用Matlab繪出TC285參數(shù)c的散點圖，如圖2(a)所示：

圖2　參數(shù)c散點及線性回歸平面圖Fig.2　Scatter and linear regression plane diagram of parameter c

從圖2(a)中可以發(fā)現(xiàn)所有點近似均勻分布在平面c=f1(T,V1)的兩側(cè)。借助Matlab分析工具，以參數(shù)c為因變量，溫度T和電勢差V1為自變量，進行多元線性回歸分析，回歸方程c=f1(T,V1)為

c=f1(T,V1)=2.982 4-0.001 9T-0.092 3V1.

(10)

經(jīng)計算，全相關(guān)系數(shù)R2=0.953 7，仿真中有10組觀測值，變量數(shù)為3，則自由度為10-3=7. 若顯著性水平α=0.05，由多元回歸相關(guān)系數(shù)臨界表[12]查得R0.05(7)=0.758. 因R=0.976 6>R0.05(7)=0.758，故回歸方程c=f1(T,V1)在α=0.05水平上顯著，即參數(shù)c與溫度T和電勢差V1線性關(guān)系密切，說明(10)式可以很好地描述器件TC285參數(shù)c與變量(T、V1)的關(guān)系。

與此類似，本文所建立的參數(shù)模型，同樣適用于TI公司的另一芯片TC253. 用相同的方法分析該器件在溫度T分別為-8 ℃、-2 ℃、8 ℃、25 ℃時的倍增增益，得到TC253的參數(shù)c值，見表2. 計算中，CMG1電壓范圍11.2 V～14.8 V，CMG2取固定值7.5 V，F(xiàn)P為1.5 V，并用Matlab多元回歸分析，得到了TC253的參數(shù)c的數(shù)學模型：

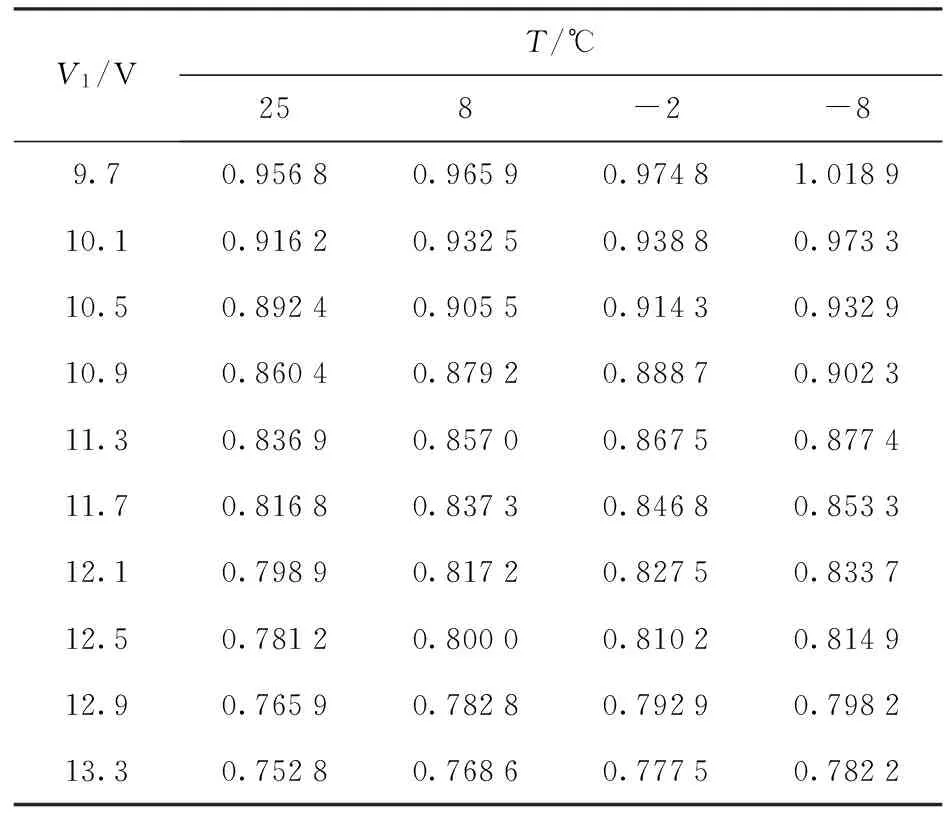
c=f2(T,V1)=2.740 6-0.001 1T-0.133 0V1.　(11)

圖2(b)表明TC253的參數(shù)c與溫度T、電勢差V1線性關(guān)系良好。經(jīng)檢驗，可以用(11)式計算TC253在給定條件下的參數(shù)c值。

4　仿真計算與結(jié)果分析

將(10)式帶入(8)式中，計算溫度范圍為-25 ℃～25 ℃時電子倍增CCD TC285的倍增特性，結(jié)果如圖3(a)所示。經(jīng)比較發(fā)現(xiàn)，由增益模型仿真計算的倍增增益曲線與TI公司的電子倍增器件TC285實際的倍增曲線[11]非常接近。

圖3　TC285和TC253的平均增益與CMG電壓的關(guān)系曲線Fig.3　Mean gains of TC285 and TC253 at different CMG voltages

同樣地，將(11)式帶入(8)式中，繪出溫度范圍為-8 ℃～25 ℃時電子倍增CCD TC253倍增增益與CMG電壓的關(guān)系曲線，結(jié)果如圖3(b)所示。該組曲線與TI公司提供的TC253數(shù)據(jù)手冊中的曲線[13]吻合良好。

為了更準確地評價本文確定EMCCD電子倍增增益方法的可靠性，分別在這兩組仿真曲線的每一條曲線上取10個計算的樣本點，如表3、表4所示，在倍增器件TC285和TC253數(shù)據(jù)手冊的給定曲線上也同樣取10個實際的樣本點[4]，利用統(tǒng)計學回歸分析的曲線相關(guān)系數(shù)理論[4]對所建立的模型進行擬合度檢驗。

TC285和TC253在不同溫度下的曲線擬合度R2，如表5、表6所示。

從表5和表6可以看出，本文基于TI公司的電子倍增器件TC285和TC253增益計算方法的曲線擬合度R2比較高，擬合度最高達到0.99以上。計算結(jié)果表明， TC285和TC253的平均增益隨CMG電壓變化的情況可以用前述方法進行準確的預測。

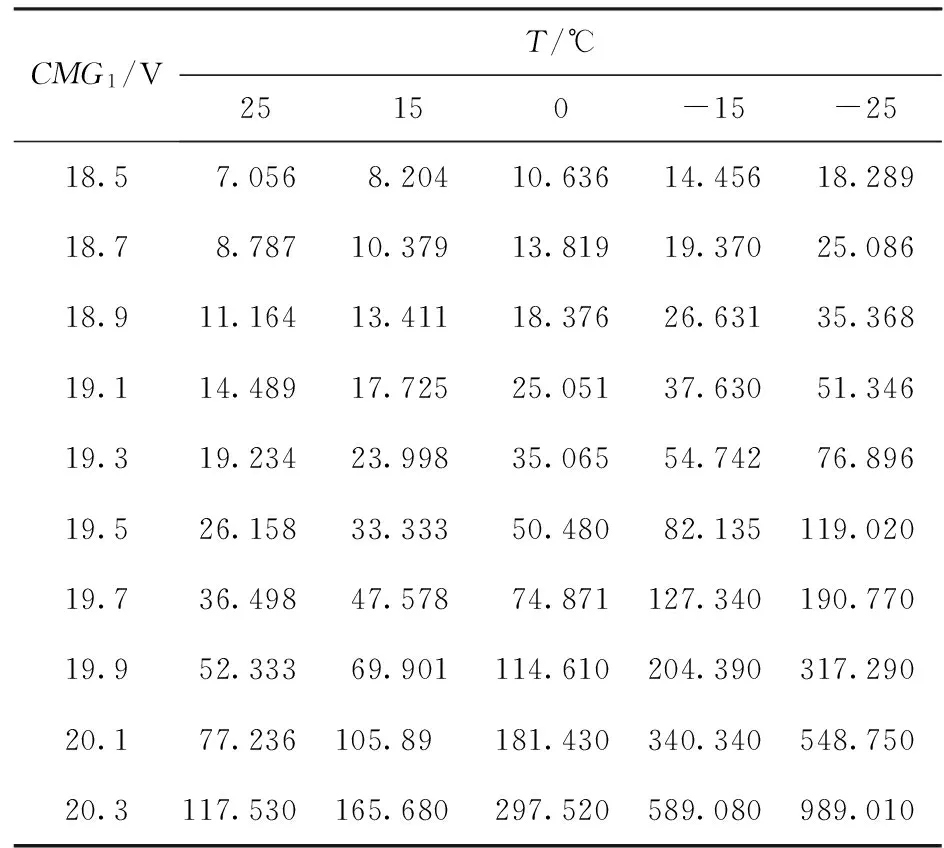
表3　TC285的仿真計算值

表4　TC253的仿真計算值

表5　TC285曲線的擬合度

5　結(jié)論

本文提出了一種確定EMCCD增益的方法，該方法通過分析Robbins[7]提出的增益模型，利用TI公司提供的EMCCD器件(TC285和TC253)數(shù)據(jù)資料，分別計算這兩種器件在該模型中的參數(shù)c值，并用多元回歸分析的方法建立了這兩種器件的關(guān)鍵參數(shù)c的數(shù)學模型，從而確定了其電子倍增增益模型的表達式。仿真計算中提取了這兩種TI公司EMCCD的樣本數(shù)據(jù)，對該增益模型進行了數(shù)值分析。結(jié)果表明，本文所提出的增益確定方法能夠方便而準確地預測EMCCD器件TC285和TC253的平均增益隨CMG電壓變化情況。該方法對于EMCCD相機設(shè)計和使用過程中所涉及的電子倍增增益的調(diào)整和校正具有參考意義。

References)

[1]Robbins M S, Hadwen B J. The noise performance of electron multiplying charge-coupled devices[J]. IEEE Transactions on Electron Devices, 2003, 50(5): 1227-1232.

[2]張聞文,陳錢. 電子倍增CCD噪音特性研究[J]. 光子學報, 2009, 38(4): 756-760.

ZHANG Wen-wen，CHEN Qian. The study of the noise characteristics of EMCCD[J]. Acta Photonica Sinica，2009，38(4): 756-760. (in Chinese)

[3]Ingley R, Smith D R, Holland A D. Life testing of EMCCD gain characteristics[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2009, 600(2): 460-465.

[4]胡泊, 李彬華. 低溫下 EMCCD 電子倍增模型[J]. 電子學報, 2013, 41(9): 1826-1830.

HU Po, LI Bin-hua. Electron multiplication model of EMCCD in low temperature[J]. Acta Electronica Sinica, 2013, 41(9):1826-1830. (in Chinese)

[5]張燦林, 陳錢, 尹麗菊. 基于單一類型載流子的電子倍增 CCD 倍增模型[J]. 兵工學報, 2011, 32(5): 580-583.

ZHANG Can-lin, CHEN Qian, YIN Li-ju. Multiplication model of electron multiplying CCD based on single type of carrier[J].Acta Armamentar, 2011,32(5):580-583.(in Chinese)

[6]Maes W, De Meyer K, Van Overstraeten R. Impact ionization in silicon: a review and update[J]. Solid-State Electronics, 1990, 33(6): 705-718.

[7]Robbins M S. Determining the multiplication of EMCCD sensor: US Patent 8,054,363[P]. 2011-11-8.

[8]Thornber K K. Applications of scaling to problems in high-field electronic transport[J]. Journal of Applied Physics, 1981, 52(1): 279-290.

[9]Valdinoci M, Ventura D, Vecchi M C, et al. Impact-ionization in silicon at large operating temperature[C]∥1999 International Conference on Simulation of Semiconductor Processes and Devices. Tokyo, Japan: IEEE, 1999: 27-30.

[10]Daigle O, Carignan C, Blais-Ouellette S. Faint flux performance of an EMCCD[J]. Proceedings of SPIE, 2006,6276:62761-62767.

[11]Texas Instruments Ltd. TC285SPD 1 004×1 002 Pixel ImpactronTMCCD Image Sensor [EB/OL]. (2003-10-15)[2005-10-15]. http:∥www.ti.com/sc/docs/stdterms.htm.

[12]楊虎，劉瓊蓀，鐘波. 數(shù)理統(tǒng)計[M]. 北京：高等教育出版社，2004: 226-227.

YANG Hu, LIU Qiong-sun, ZHONG Bo. Mathematical statistics[M]. Beijing: Higher Education Press, 2004:226-227. (in Chinese)

[13]Texas Instruments Ltd. TC253SPD 680×500 Pixel ImpactronTMCCD Image Sensor [EB/OL]. (2003-07-15)[2005-09-15]. http:∥www.ti.com/sc/docs/stdterms.htm.

A Method of Determining EMCCD Electron Multiplication Gain

LU Jia-li， LI Bin-hua， HU Po

(Faculty of Information Engineering and Automation， Kunming University of Science and Technology， Kunming 650500，Yunnan, China)

The electron multiplication gain needs to be corrected during operation of the EMCCD camera. According to the structural characteristics of the electron multiplying CCD and the charge multiplication of the single stage multiplier, the limitation of the existing multiplication model has to be analyzed in practical application. For TI EMCCD devices, the key parameters , including the operation voltage and temperature of EMCCD, of original multiplication model can be derived by simulation, a mathematical equation of the parameters is also presented by multiple regression analysis. And then the equation is introduced into the model, and a new method for determining the EMCCD gain is obtained, which is universal and simpler. It expands the application range of the original multiplication model. The simulation results of the model agree well with the actual data of EMCCD device. It shows that, the gain model is convenient for calculating the electron multiplier average gain as the charge multiplication gate voltage is changed.

optoelectronics and laser technology; EMCCD; electron multiplication gain; parameter calculation; simulation analysis

2014-05-23

國家自然科學基金委員會與中國科學院天文聯(lián)合基金項目(10978013)

盧家莉(1988—)，女，碩士研究生。E-mail:851988440@qq.com;

李彬華(1963—)，男，教授，碩士生導師。E-mail:lbh@bao.ac.cn.

TN29

A

1000-1093(2015)04-0710-06

10.3969/j.issn.1000-1093.2015.04.020