改進的FOA算法在通用橋式起重機輕量化設計中的應用

劉 彬 蔣惠波 吳曉路

（濟寧職業技術學院 濟寧 272037）

改進的FOA算法在通用橋式起重機輕量化設計中的應用

劉 彬 蔣惠波 吳曉路

（濟寧職業技術學院 濟寧 272037）

針對傳統FOA算法全局收斂能力差、易陷入局部極值的缺陷，提出了具有混 映射及協同進化功能的改進果蠅算法。首先利用Logistic混 映射功能在整個收斂域范圍內搜索并初始化果蠅種群，保證算法的全局計算能力，然后根據當前果蠅個體的位置賦予搜索的方向與距離，以期全面提高算法的計算速度。采用兩個優化函數測試改進后算法優化的特性，優化計算的結果顯示了該算法具有良好的全局優化能力，在通用橋式起重機金屬結構輕量化設計中的成功應用，體現了該算法在結構設計輕量化方面的優越性。

FOA Logistic 協同進化 優化設計

模擬果蠅覓食行為的果蠅算法［1］（Fruit Fly Optimization Algorithm - FOA）自2011年提出以來，因其簡單的計算原理、快速的計算能力及良好的通用性，成為了智能優化領域新的研究熱點。國內外研究人員以各自的研究背景為依托，提出了各種各樣的改進FOA算法，以期提高其優化和解決實際問題的能力。Wang Li［2］等人采用FOA算法求解多維背包問題，使用二進制串表示問題的解決方案，并且將算法的進化定義為三個主要的搜索過程，通過數值算例的仿真及與其他算法的比較結果證明了該 算法可靠的計算能力；Li H.Z.［3］等人將FOA算法應用到廣義回歸神經網絡中，將FOA算法同廣義 回歸神經網絡結合，用于預測年度電力負荷狀況；Yuan Xiaofang［4］等人為提高算法的全局搜索能力，采用了多個種群同時參與尋優迭代，提出了多種群優化算法（Multi-Swarm Fruit Fly Optimization Algorithm）。

筆者針對FOA算法進行了大量的研究，掌握了FOA算法的優化能力及其不足之處，針對傳統FOA算法全局搜索能力差，迭代搜索的目標不明確等問題，本文提出了相應的改進方案。首先，初始化的果蠅種群采用Logistic混沌映射的方式產生，利用混沌的遍歷性和隨機性，在全局范圍內隨機的初始化果蠅種群，使算法在搜索初期具有較好的全局性。其次，利用果蠅個體間的位置關系，確定果蠅繼續飛行的方向和距離，提高了算法的計算速度和收斂域最優點的精度。

1 改進的FOA算法

作為全新的基于果蠅覓食行為全局智能優化算法，FOA算法簡單易理解，程序代碼容易實現，和其他智能算法相比，FOA算法更簡單、優化計算的穩定性更強，更容易轉化為生產力。將傳統果蠅算法同本文的改進方式結合，其優化計算的步驟如下：

4）利用已生成的隨機矩陣，生成如圖1所示的設計變量矩陣。

5）計算種群目標函數值fitnessm，

6）判斷算法是否收斂，是則輸出結果，否則執行下一步。

7）以當前最優果蠅為起點，種群中任意個體按照式（4）搜索新解。

8）返回步驟5。

2 數值算例驗證

為驗證算法的性能，采用了2個被廣泛用來測試算法性能的優化測試函數。種群中包含的果蠅個體取Population=20，設計空間的維數分別取Design_ Num=10和Design_Num=30，最大迭代次數Max_ Num=400，收斂精度取為0.000001。分別運用FOA算法和改進后的算法對測試函數進行分析，優化的結果見表1，目標函數的迭代曲線如下圖2、圖3所示。

1）Rastrigin's function：Rastrigin是一個高度多峰的測試函數，在收斂域內存在多個局部極值，該函數考驗算法的全局收斂能力。

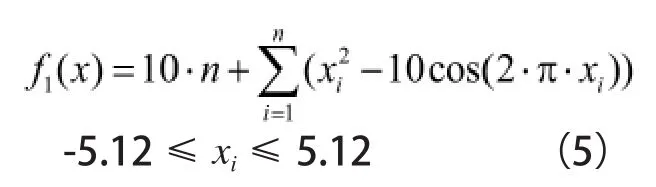
2）Rosenbrock's Valley：該測試函數也稱為香蕉函數，其全局最優值分布在一個狹長的、平坦的谷底，很難搜索到全局最優值。

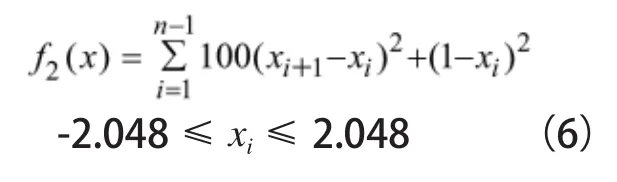
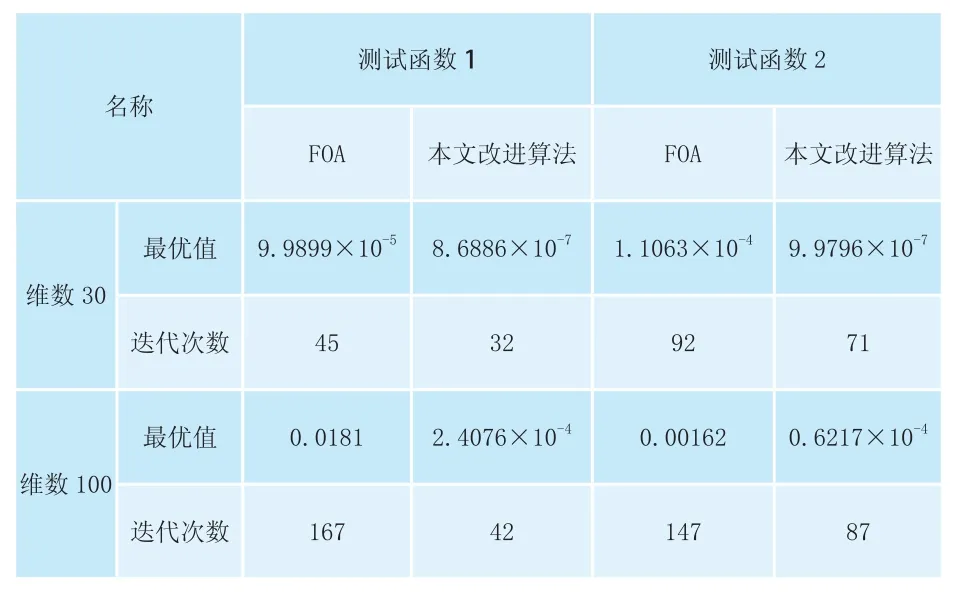
表1 測試結果

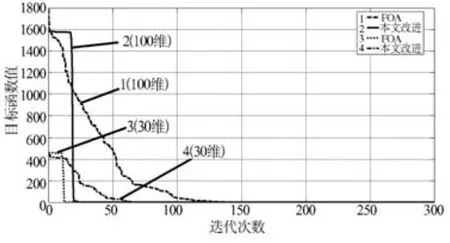
圖2 測試函數1迭代曲線

圖3 測試函數2迭代曲線

參照圖2、圖3的迭代曲線及表1的計算結果可知，采用本文提出的改進方法同傳統FOA算法相比，具有明顯的優勢，計算量上具有明顯的降低趨勢，而且計算精度更高，該算法具有應用于工程優化設計的潛力。

3 橋式起重機結構優化

以如圖4所示的傳統的橋式起重機作為優化的目標，選擇能夠直接影響起重機工作性能同時又能夠改變起重機外觀形態的10個變量作為設計變量，10個設計變量所代表的幾何意義如圖5和圖6所示，分別是：主梁上蓋板厚度4mm≤X1≤24mm，主梁下蓋板厚度4mm≤X2≤24mm，主梁主腹板厚度4mm≤X3≤24mm，主梁副腹板厚度4mm≤X4≤24mm，主梁腹板高度400mm≤X5≤800mm，主梁腹板間距190mm≤X6≤290mm，端梁上下蓋板厚度4mm≤X7≤10mm，端梁腹板厚度4mm≤X8≤10mm，端梁腹板高度388mm≤X9≤788mm，端梁腹板間距220mm≤X10≤320mm。本文選用起重量為5t，跨度10.5m的通用雙梁橋式起重機，對其結構進行分析及輕量化設計。

圖4 通用橋式起重機結構模型

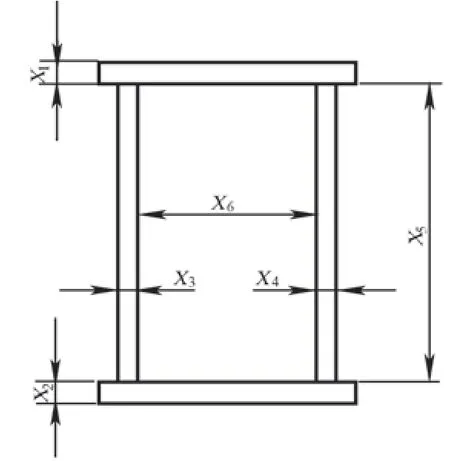
圖5 主梁截面尺寸表達

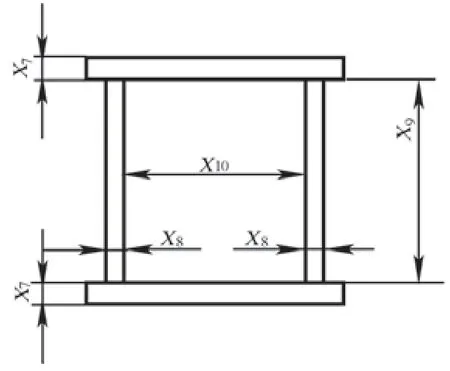
圖6 端梁截面尺寸表達

結構輕量化設計的目標是在保證滿足結構設計要求的前提下，所使用的材料最少，即結構質量最輕，因此可以將起重機輕量化設計的目標函數定義為：

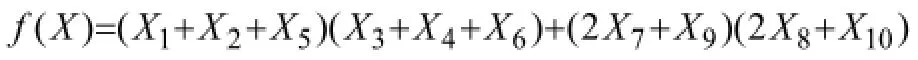
約束條件：橋式起重機結構設計需要遵照起重機行業設計規范GB 3811—2008，保證起重機結構設計的強度、剛度及穩定性的設計要求，并按照實際制造工藝條件及尺寸限制等方面的限制。

采用本文改進算法對通用橋式起重機金屬結構進行輕量化設計，對算法進行20次獨立的優化計算，將優化所得結果列于表2中，表2中包含了20次獨立優化計算的最優、最差及平均計算結果。通過表2中數據可知，采用改進的FOA算法對通用橋式起重機進行輕量化設計可以獲得較好的計算結果，原始設計參數為某款通用橋式起重機的實測數據，設計余量較大，而優化后的最優解相較原始參數目標函數下降約36.56%，若該起重機采用本文方法進行設計，可以較大程度的節約成本，節約原材料的損耗，獲得可觀的經濟效益。對比優化后的平均結果和最優解，目標函數的變化率僅為4.67%，本文算法的穩定性（魯棒性）較好，計算結果不會出現較大的波動。

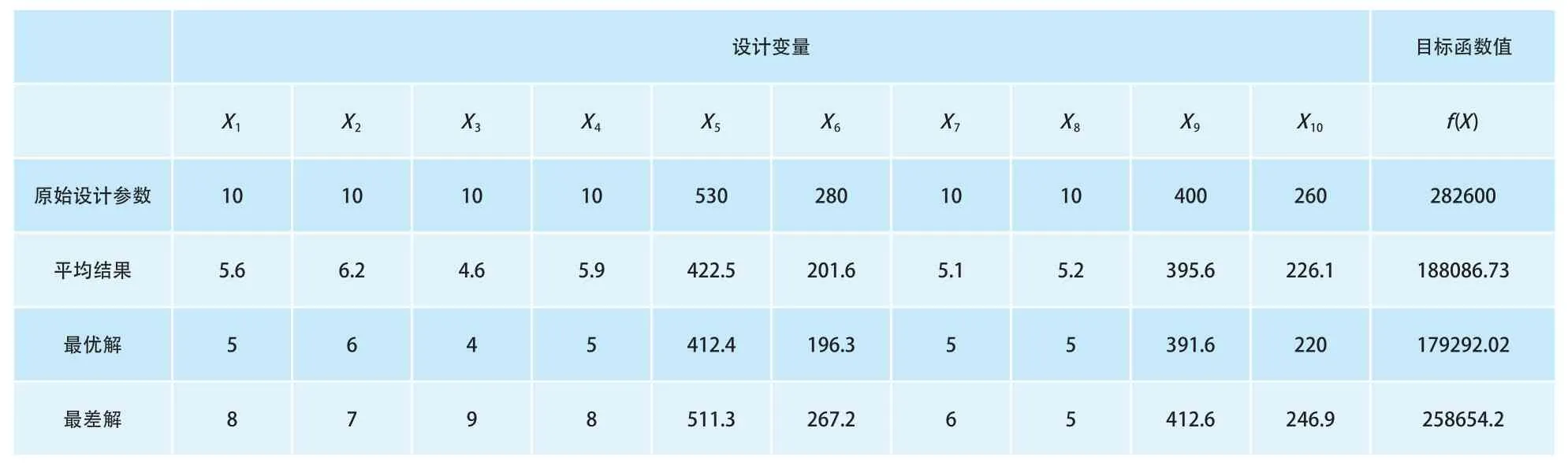
表2 優化計算結果

4 結論

本文提出了一種具有更快計算速度的全局FOA算法，結合Logistic混沌映射準則，利用混沌的遍歷性和不確定性，在搜索空間混沌初始解，保證了算法計算起點的混沌性和全局性。根據當前果蠅個體的坐標，確定下一次迭代的搜索向量，保證了算法能夠自適應的搜索更優解。通過對兩個數值算例的分析及同傳統FOA算法的比較，證明了本文改進方案的快速收斂及精度高的特性，將改進后的算法運用到通用橋式起重機金屬結構的優化設計之中，對該算法解決實際問題的能力進行了驗證。

［1］ 潘文超.最新演化式計算技術——果蠅優化算法［M］.臺灣：滄海書局，2011.

［2］ Wang L.， Zhang X.L.， Wang S.Y.. A novel binary fruit fly optimization algorithm for solving the multidimensional knapsack problem［J］.Knowledge-Based System，2013，48：17-23.

［3］ Li H.Z.， Guo S.， Li C.J.， et al.. A hybr id annual power load forecasting model based on generalized regression neural network with fruit fly optimiz ation algorithm［J］.Knowledge-Based System，2013，37：378-387.

［4］ Yuan Xiaofan， Dai Xiangshan， Zhao Jingyi， et al.. On a novel multi-swarm fruit fly optimization algorithm and its application［J］.Applied Mathematics and Computation，2014，233： 260-271.

［5］ 殷成鳳.門座起重機人字架有限元分析［J］.建設機械技術與管理，2001（11）：24-25.

［6］ 謝光輝.機械優化問題的MATLAB求解方法［J］.煤炭技術，2001（9）：43-44.

［7］ 姜潮，張哲，韓旭，等. 一種基于論據理論的結構可靠性分析方法［J］.力學學報，2013，45（1）：103-114.

［8］ 鄧亮，趙進，王新.基于遺傳算法的網絡編碼優化［J］.軟件學報，2008，19（8）：2269-2279.

The Improved FOA Algorithm Applied in the Shaft Bracket Structure Optimization Design Optimization Design

Liu Bin Jiang Huibo Wu Xiaolu
（Electrical Engineering of Jining vocational technical college Jining 272037）

In view of the poor global convergence ability of traditional Fruit Fly Optimization Algorithm（FOA algorithm）， and it is easily trapped in local minima， an improved FOA algorithm is proposed which has the function of chaotic mapping and cooperative co-evolution. Firstly， using the function of Logistic chaotic mapping for searching and initialize the drosophila population within the entire domain of convergence， to ensure the global computing ability of the algorithm， then taking advantage of the position of current flies to confirm the search direction and distance， so that the global computing ability of the algorithm can be confirmed. The improved algorithm is tested by two optimization function， the testing result shows that the algorithm has good global optimization ability. The successful application for the a-frame structure proves that the algorithm can be conducted to comprehensive promotion in the fi eld of mechanical optimization design.

FOA Logistic Co-evolution Optimization design

X941

B

1673-257X（2015）04-04-04

10.3969/j.issn.1673-257X.2015.04.002

劉彬（1980～），女，講師，主要從事機械設計與制造工作。

2014-07-31）