耦合諧振式無線電能傳輸系統的線圈優化

肖思宇 馬殿光 張漢花 姚 辰 唐厚君

（上海交通大學電氣工程系 上海 200240）

1 引言

磁耦合諧振式（Coupled Magnetic Resonance,CMR）技術是 2006年在美國物理學工業物理論壇上被第一次提出的，隨后通過理論分析證實了該種無線電能傳輸方式的可行性。2007年美國 MIT的物理研究小組以“耦合模理論”為理論依據，通過實驗驗證了具有相同諧振頻率的兩個諧振體可以通過磁耦合形式實現電能的無線傳輸，并可以獲得較高的傳輸效率[1]。

CMR技術采用諧振線圈間磁場的耦合，通過發射線圈和接收線圈的共振來實現能量的無線傳輸。當發射線圈和接收線圈達到諧振狀態時，系統可經由損耗最低的路徑將電能從供電端傳輸到受電端，最大程度地確保能量傳輸的效率。根據近區磁場的特點，在近區場內具有相同諧振頻率的振蕩體會發生波耦合，實現能量在兩個諧振體之間的傳輸。由于諧振體的共振波長遠遠大于振蕩器尺寸，能量傳輸幾乎不受附近物體的影響，能量在傳輸過程中損失很小，也不會對周圍環境產生影響，因此 CMR技術是一種高效、可靠的無線電能傳輸方式。

但是，由于磁耦合諧振式無線電能傳輸系統在設計時存在理論偏差和實際損耗，其傳輸效率會隨著傳輸距離的增大而急劇減小，因此進一步研究磁耦合諧振式傳輸系統的傳輸特性對于如何提升供電端與受電端的耦合程度、設計最優的線圈結構以提高傳輸效率有著重要的理論意義和實用價值。

本文針對耦合諧振式無線電能傳輸系統進行了研究與設計。采用耦合模理論對系統建模，利用COMSOL軟件對磁耦合諧振式系統的線圈結構進行仿真，研究了線圈結構參數對系統傳輸效率的影響，并提出了在固定線圈距離時線圈參數優化的方案。

2 系統數學模型

2.1 耦合模公式的推導

將單個諧振線圈等效為一個 LC串聯回路，如圖1所示。

圖1 諧振線圈等效電路Fig.1 Equivalent circuit of the resonance coil

由歐姆定律可得電壓電流表達式：

將一階微分方程式（1）與式（2）互相代入，可得關于電壓和電流的二階微分方程：

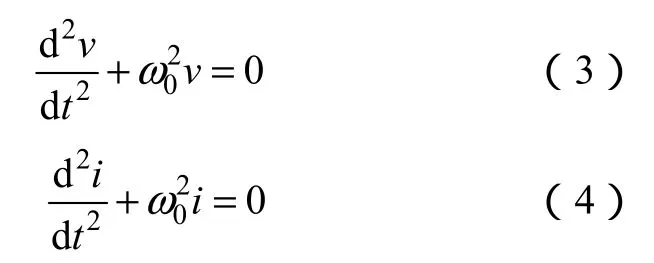
式中，i為諧振電路電流；v為電感的端電壓；ω0=為諧振角頻率。

在考慮系統損耗的情況下，引入系統損耗后有[2]

式中，Γ為損耗系數。

可得耗散功率W的表達式：

2.2 兩諧振體系統耦合模型

假設耦合諧振式無線電能傳輸中，兩個諧振體的諧振頻率分別為ω1和ω2，則在不計損耗的情況下該系統的耦合模型可用下述方程組表示[2]

式中，κ12和κ21為線圈1與線圈2之間的耦合系數，當ω1且ω2時系統為弱耦合，此時相比而言較小，僅當ω1與ω2接近時耦合才會影響a1、a2的變化（ a1、a2的含義與式（6）中類似）。

在系統能量守恒時，κ12和κ21存在相互約束的關系。由于系統能量變化率為零，故有

式中，a*為a的共軛；κ?為κ的共軛；Re()為實部運算符；Im()為虛部運算符。

由于 a1和 a2的實部和虛部為非特定值，故耦合系數滿足表達式：

假設諧振體2初始沒有能量，則根據式（8），從諧振體1耦合到諧振體2的平均功率表達式為

又當互感系數為M時，從諧振體1耦合到諧振體2的諧振功率在一個周期內的平均值可表示為

比較式（10）和式（11），可得耦合系數的表達式為

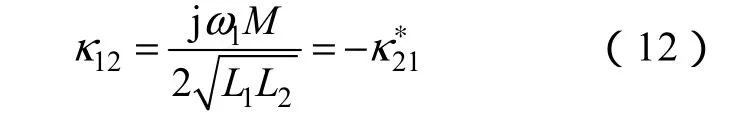
現考慮一般情況，即有輸入源、負載、異物擾動以及損耗的環境，由式（7）經過變換可得源端和負載端的耦合模型表達式為

式中，as、ad為發射端、負載端的模式幅值復變量；Γd [e]為考慮異物擾動下的接收線圈損耗率（包括輻

射損耗Γrad和吸收損耗Γabs），故有Γd[e]=+，類似有帶擾動的源損耗率為Γs[e]；κsd[e]和κds[e]為考慮擾動因素時的發射/接收端耦合系數；us為電源對系統的影響；Γwork為負載損耗率；

定義有效功率傳輸效率：

3 系統仿真

3.1 線圈結構對系統傳輸效率的影響

（1）線圈繞制方式對耦合系數的影響

a）半徑為R=30 mm的圓形線圈間的耦合系數

改變圓形線圈間每匝線圈的間距，得到線圈耦合因數的變化規律，如圖2所示。圓形線圈達到的最大線圈耦合因數為0.195，此時對應的間距為18 cm。

b）相同面積下矩形線圈間的耦合因數（60 mm×60 mm）

改變矩形線圈每匝線圈的間距，線圈耦合系數的變化如圖3所示。矩形線圈所達到的最大線圈耦合因數為0.194，此時對應的間距為23 cm。

圖2 圓形線圈耦合系數隨每匝線圈間距的變化Fig.2 Circular coil coupling coefficient changes with the spacing of each turn of the coil

圖3 單矩形線圈耦合系數隨每匝線圈間距的變化Fig.3 Single rectangular coil coupling coefficient changes with the spacing of each turn of the coil

c）相同面積情況下，雙矩形線圈間的耦合因數在保持面積相同的條件下，將單個矩形線圈分為2個矩形線圈，如圖4所示。此時線圈間的耦合因數最大為0.062。

圖4 雙矩形線圈耦合系數隨每匝線圈間距變化Fig.4 Double rectangular coil coupling coefficient changes with the spacing of each turn of the coil

由此可知，相同面積情況下，圓形線圈與矩形線圈間的耦合強度相差不大，但將整體區域劃分后再繞制線圈會急劇減小線圈間的耦合強度。此外矩形線圈在拐角處電流密度分布不均勻，會增大線圈的損耗參數。因此，采用圓形線圈可以提高線圈間的耦合強度，同時能夠減小線圈損耗，是一種優化的線圈繞制方式。

（2）線圈排布寬度對耦合系數的影響

當收發線圈距離 D=40 mm，線圈半徑為R=30 mm，線圈匝數為5時，逐漸改變同一平面內每匝線圈之間的間距，可得兩線圈之間耦合因數的變化規律，如圖5所示。

圖5 圓形線圈耦合系數隨線圈間距變化Fig.5 Circular coil coupling coefficient changes with the coil spacing

由圖可見，當線圈距離和半徑固定時，線圈間的耦合系數隨每匝線圈間距的增大先增大后減小，即存在最優的線圈間距使得線圈間的耦合強度最大在本例中，當線圈各匝之間的間距為12 mm時，耦合強度最大。

（3）線圈半徑對耦合系數的影響

由圖6可知，線圈間的耦合系數隨著半徑的增大而增大。但線圈耦合強度隨半徑增大而增大的速率逐漸減緩，即半徑對線圈耦合強度的影響越來越小。由圖7可知，線圈半徑越大，耦合系數隨線圈距離變化越平緩，系統傳輸距離也越大。

圖6 線圈耦合系數隨線圈半徑變化Fig.6 Coil coupling coefficient changes with the coil radius

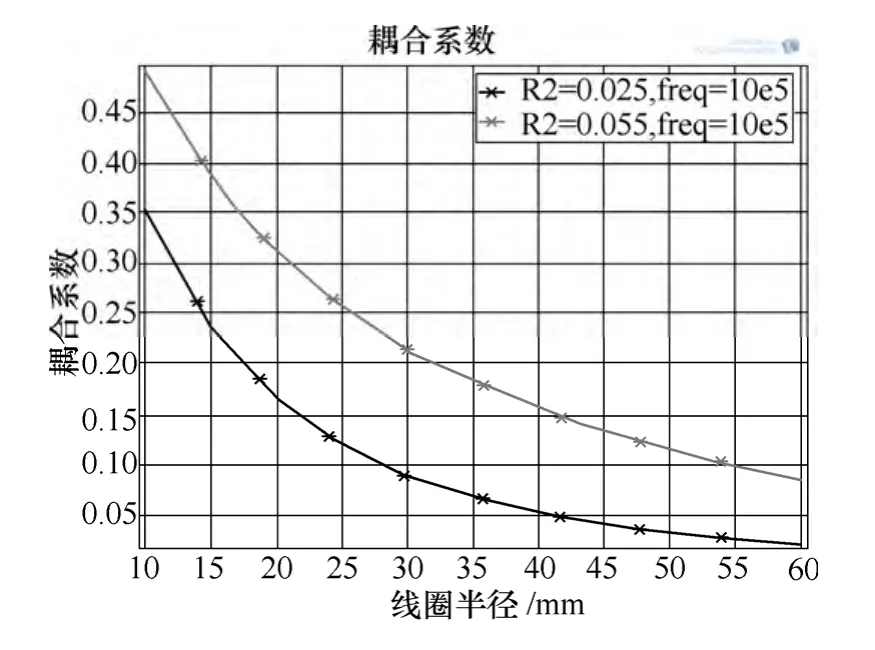
圖7 不同半徑下線圈耦合系數隨線圈距離變化Fig.7 Different radius coil coupling coefficient changes with the coil distance

3.2 距離固定時兩線圈系統的效率優化方案

當傳輸距離固定為40 mm時，對系統進行線圈優化設計的步驟為：

（1）線圈半徑的優化

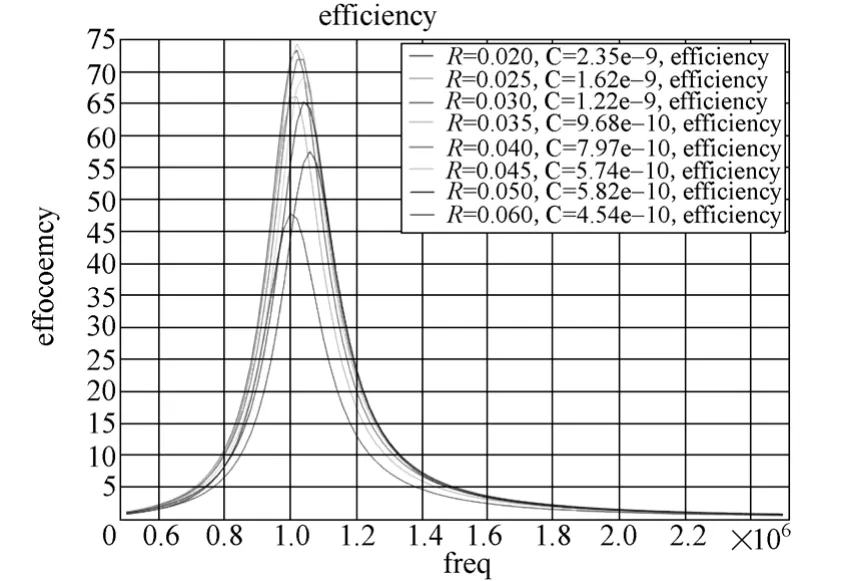
圖8 固定線圈匝數對線圈半徑的優化Fig.8 Optimization of radius for fixed turns of the coil

圖9 線圈半徑固定時對線圈匝數的優化Fig.9 Optimization of turns for fixed turns of the coil

增大收發線圈半徑，并匹配電路的諧振電容，使得線圈諧振頻率固定為1 MHz，由上圖可知，當線圈半徑R=35 mm時，系統的傳輸效率最高，約為72%。

（2）線圈匝數的優化

固定線圈半徑為35 mm，增加收發線圈的匝數，并匹配電路的諧振電容，使得線圈諧振頻率固定為1 MHz，得到系統傳輸效率隨線圈匝數變化的趨勢如圖9所示。由圖可知，當線圈匝數為15時，系統傳輸效率最高。

（3）線圈匝間距的優化

固定線圈半徑為R=35 mm，線圈匝數為15，改變每匝線圈間的間距，得到系統效率的變化趨勢如圖10所示。由圖可知，每匝線圈間距的改變對系統傳輸效率的影響不是很明顯，系統效率隨線圈排布間距先增大后減小。當整體排布寬度為14 mm時，系統傳輸效率最大。

圖10 固定線圈匝數、半徑對線圈排布間距優化Fig.10 Optimization of coil arrangement pitch for fixed coil turns and radius

4 結論

本文在 COMSOL仿真平臺下，詳細研究了線圈參數（線圈繞制方式，線圈半徑，每匝線圈的間距等）對系統傳輸效率的影響規律。主要結論如下：

（1）相同面積時，采用圓形線圈可以增大耦合系數，降低線圈自身損耗，從而提高系統傳輸效率。將線圈分開繞制會明顯降低線圈間的耦合系數。

（2）系統傳輸效率隨著線圈半徑的增大會先增大后減小，存在最優化的線圈半徑使得系統效率最大。當線圈半徑和匝數固定時，改變每匝線圈間的間距也會影響系統的傳輸效率。隨著每匝線圈間距的增大，傳輸效率先增大后減小。

（3）當線圈間的距離固定時，線圈參數的優化方案為：先優化線圈半徑，再優化線圈匝數，最后優化線圈的匝間距。當傳輸距離為40 mm時，通過優化可以將系統效率由原來的35%提高到 72%左右。

[1] Kurs A,Karalis A,Moffatt R,et al.Wireless power transfer via strongly coupled magnetic resonances[J].Science,2007,317(5834):83-86.

[2] H.A.Haus.Waves and Fields in Optoelectronics[M].Prentice-Hall,New Jersey,1984:197-216.

[3] Karalis A,Joannopoulos J D,Solja?i? M.Efficient wireless non-radiative mid-range energy transfer[J].Annals of Physics,2008,323(1):34-4.