磁性液體微壓差傳感器動態建模研究

劉雪莉 楊慶新 楊文榮

（1.河北工業大學電磁場與電器可靠性省部共建重點實驗室 天津 300387；2.天津工業大學電工電能新技術天津市重點實驗室 天津 300387）

1 引言

磁性液體是一種將納米級鐵磁材料顆粒利用表面活性劑均勻、穩定地分散在某種液態載體之中，所形成的穩定膠體懸浮液[1]。由于其兼具良好的流動性和超順磁性，被廣泛應用在密封、航天、傳感測量、生物醫學和環保等領域[2-4]。近年來，基于磁性液體的各類傳感器不斷涌現[5-11]，傳感器的動態特性卻較少提及[12]。而傳感器的動態性能是傳感器特性的重要指標之一，因此對磁性液體傳感器的動態特性進行分析建模，有利于此類傳感器的進一步發展。

由于磁性液體的傳感器多數涉及磁場、流體場共同作用的環境，會出現磁—機耦合、流—固耦合、氣—液耦合等情況，因此，傳感器的動態性能會受到較多因素的影響，且磁性液體的粘度在磁場中的變化也是重要的影響因素。現有研究有基于能量守恒定律對微壓差傳感器動態特性進行分析的[13]，但未考慮磁性液體的磁粘特性。

本文分析了課題組設計的磁性液體微壓差傳感器的基本結構，闡述了其工作原理；而后對傳感器內部的磁場和流體場進行分析，考慮了粘度在磁場中的變化，根據流體運動學理論，建立了分步耦合與強耦合模型，以表征傳感器的動態特性；最后對該模型進行了仿真，結果與理論推導值具有一致性。

2 微壓差傳感器的基本原理

本文設計的磁性液體微壓差傳感器結構模型如圖1所示，U形玻璃管中裝有磁性液體，初始液面位于線圈的中部，每個管臂外有兩組完全對稱的線圈，其中激勵線圈1和3，作為產生磁場的激勵源；感應線圈2和4，用于測量感應電壓u2和u4。

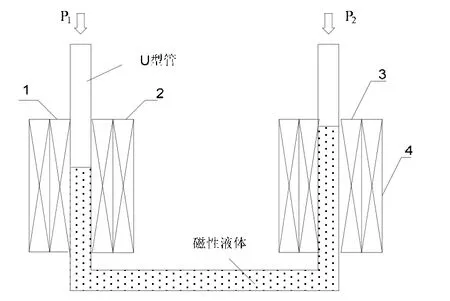
圖1 磁性液體微壓差傳感器模型圖Fig.1 Model for the differential pressure sensor

線圈1和3正向串接，線圈2和4反向串接。其等效電路如圖2所示，i為激勵源，Li（i=1，2，3，4）為4個繞組的電感值，Ri（i=1，2，3，4）為4個繞組的電阻值。

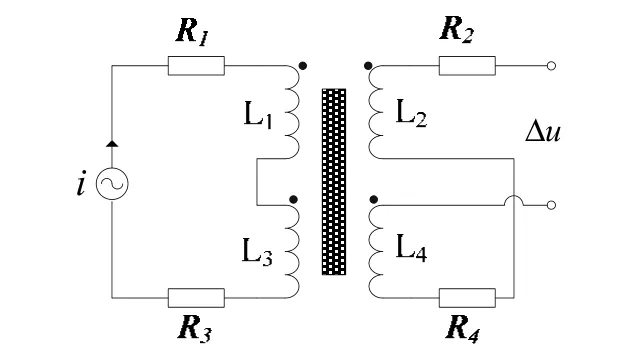
圖2 微壓差傳感器的等效電路Fig.2 Equivalent circuit of pressure sensor

激勵繞組加正弦電流 i，該電流產生一個交變磁場。當U形管兩端壓力差ΔP=P1?P2≠0時，試管兩側因為磁性液體的液面高度不同而磁場分布不同，則兩線圈產生感應電壓差Δu=u2?u4≠0。ΔP越大，液面高度差越大，則Δu越大。

激勵線圈施加正弦電流i

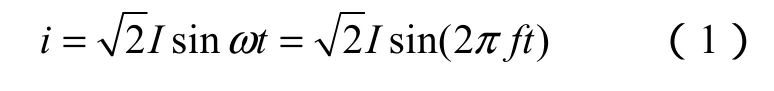
激勵線圈的電壓為

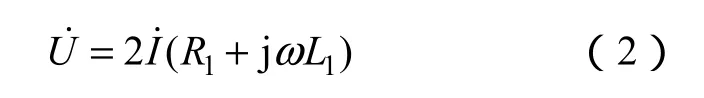
式中，R1、L1分別為激勵線圈的等效電阻和電感。

U形管左右兩側的感應電壓有效值為

式中，Ma和Mb分別為U形管左右兩側的激勵線圈對感應線圈的互感系數。則U形管左右兩側的感應電壓差有效值為

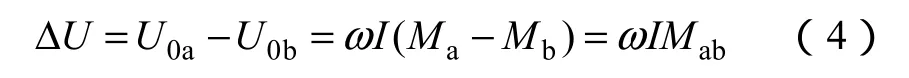
無壓力差時U形管兩端的液面高度相等，存在壓差Δp時，磁性液體由高壓端向低壓端流動，產生液面高度差為Δl，忽略管臂線圈內的磁場梯度，即認為磁場是均勻的，忽略磁性液體所受磁場力和粘性力，則有

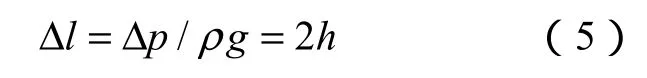
式中，h為磁性液體單側管臂中移動的距離；ρ為磁性液體密度；g為重力加速度。

由于磁性液體的流動，兩側線圈的互感 Ma和Mb不再相等，使輸出電壓差ΔU發生變化。

3 微壓差傳感器耦合模型

3.1 分步耦合模型

磁性液體微壓差傳感器中的磁場主要由U形管兩臂上的線圈提供，激勵線圈通入的是正弦交流電，故管內部的交變電磁場是交流正弦變化的電磁場。忽略位移電流，麥克斯韋方程組微分形式可以表示為[14]：

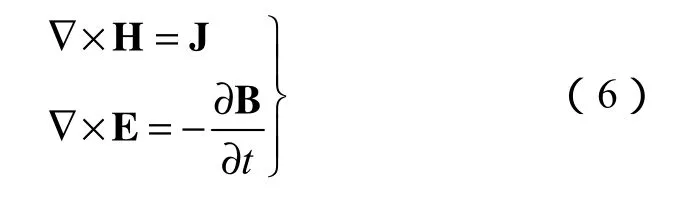
式中，B為磁感應強度，H為磁場強度，J為傳導電流。

磁性液體是對周圍電磁場能夠做出響應，并且和電磁場相互影響的流體，在沒有外加磁場時沒有磁性，在外加磁場下，表現為超順磁性。磁性液體在外磁場中受到的磁場力來源于其中的固相磁性顆粒，在外磁場作用下，各個固相微粒都發生不同程度的磁化。每個磁化分子都在其周圍形成磁場。取磁性液體中的一個微元控制體作為分析單元，該微元體內必包含大量固相微粒，按分子電流觀點[15]，每個固相顆粒可用一個分子電流環來替代，其磁化強度M =B'/μ0可用環形電流表示，全部微粒的磁化強度的矢量和就是整個微元體的磁化強度。

磁性液體內總的磁感應強度B可表示為

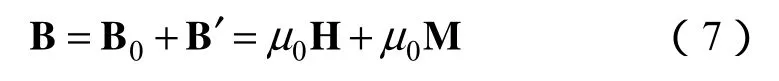
式中，B0是外磁場的磁感應強度，B'是物質磁化產生的附加磁感應強度，μ0是真空磁導率，M是磁化強度矢量。

定義矢量磁位A，滿足

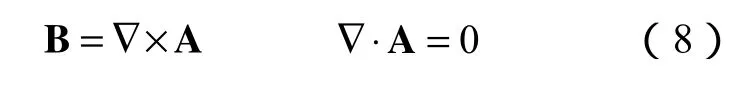
根據矢量場旋度的概念可得

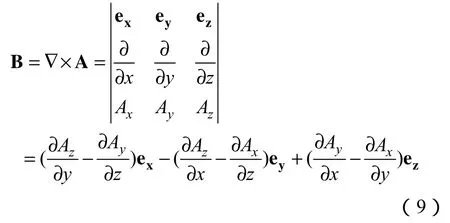
根據磁性液體的磁化強度曲線，若傳感器激勵線圈內的磁場小于 200Gs，磁性液體工作在線性區域，則有

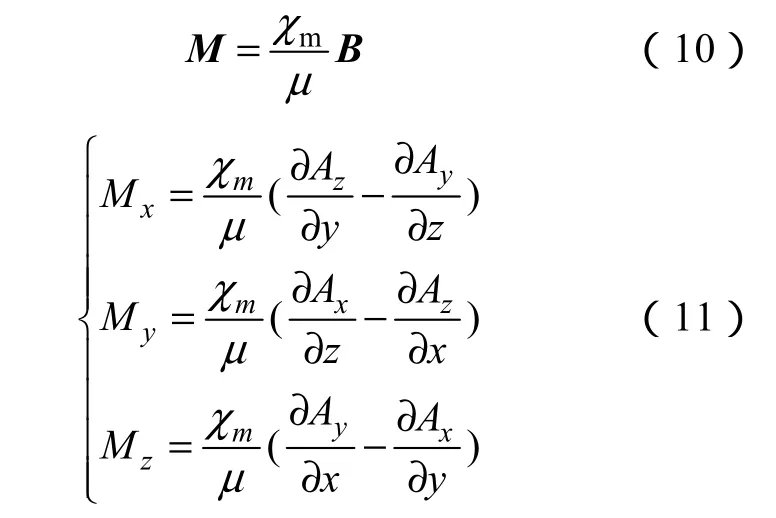
式中，χm為磁性液體的磁化率。

微壓差傳感器模型中存在磁場—流體場—熱場等多場的耦合作用，考慮磁性液體流動所帶來的溫升較小，可忽略溫度的影響，簡化建立磁場—機械場（流體場）的有限元模型，其相互耦合關系如圖3所示。

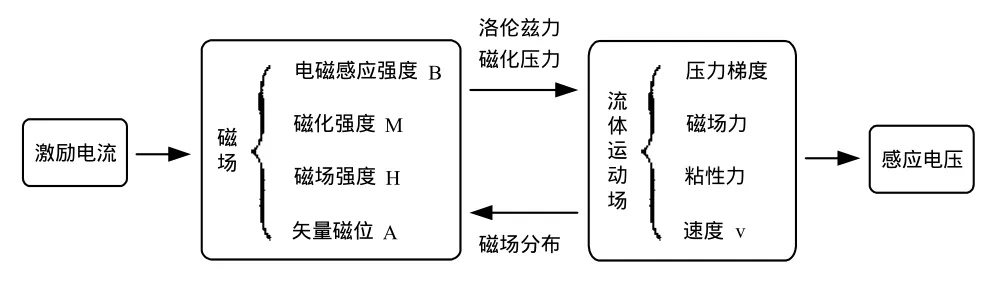
圖3 分步耦合關系圖Fig.3 Step by step coupling relationship

用不可壓縮粘性流體的運動微分方程表示磁性液體在U形管中的運動，為

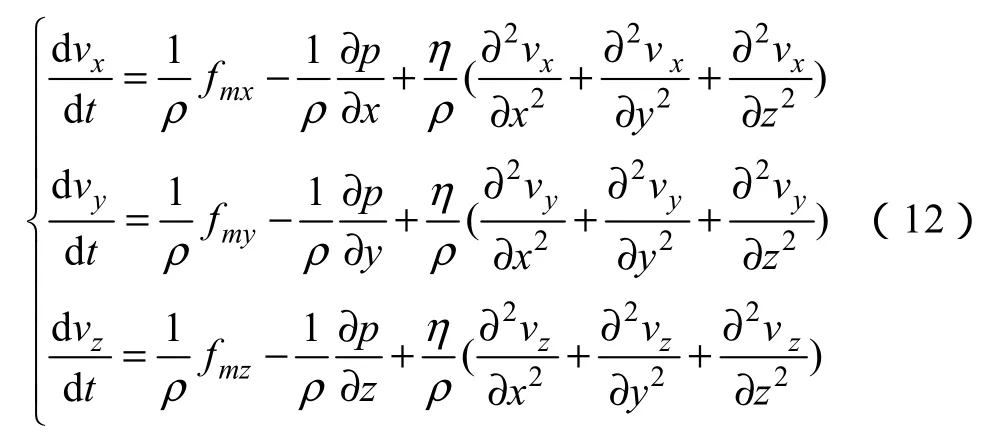
式中fmx，fmy，fmz為磁性液體x，y，z三個方向所受的磁場力，vx、vy、vz分別為磁性液體沿x，y，z方向的速度，η為磁性液體的粘度。

單位體積的磁性液體在流體場中所受的磁場體積力為F，即[16]

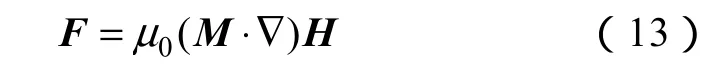
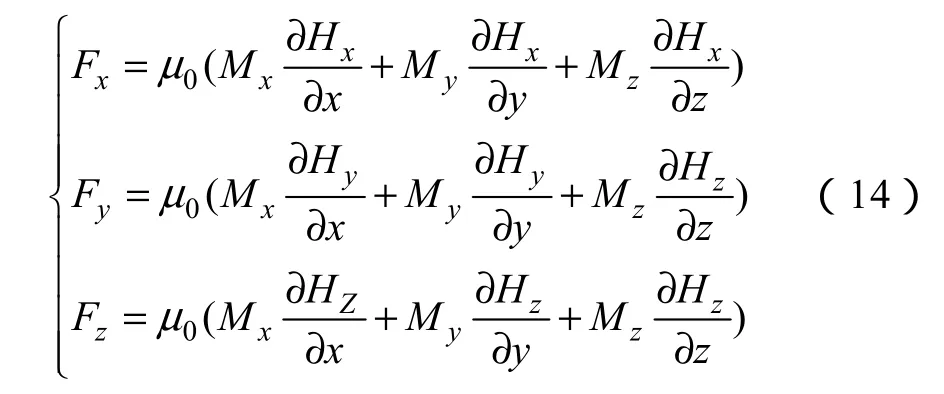
聯立式(12)、(14)可得，磁性液體在磁場中的運動方程

Γ1和Γ2是微壓差傳感器內部磁性液體的力學邊界條件和磁學邊界條件：

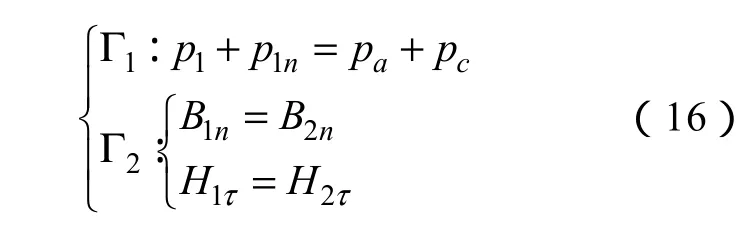
式中pa為大氣壓力，pc為磁性液體的表面張力，下標“1”表示磁性液體邊界的內側，下標“2”表示磁性液體邊界的外側。

微壓差傳感器內部磁性液體的初始條件：液體速度場為零，外部激勵磁場恒定。

由式（15）可知，磁場對磁性液體產生的體積力和外界壓力影響流體場中磁性液體的流速，流速的變化會影響到U形管兩側液面差的產生，即磁性液體微壓差傳感器磁芯位置發生改變，進而影響到磁場的分布，這就是傳感器的磁-機械耦合效應。

假定磁性液體處于靜止狀態，計算磁場分布，由此磁場分布進行流體運動場的計算，根據新的運動場，假定液體靜止，再次計算磁場，計算出的磁場再次進行運動場計算，直至誤差滿足條件停止迭代，由此時的磁場分布可求得U形管兩臂的感應電壓差，以此表征兩側壓力差，圖4即為分步耦合算法的迭代流程。

圖4 分步式弱耦合算法的迭代流程圖Fig.4 Iterative flow chart of step by step coupling algorithm

3.2 強耦合模型

上述分步耦合模型，磁場和流體運動場在計算時，均假設一種場是固定的，進行相互的迭代；但在實際中，微壓差傳感器內部的磁場和流體場每一個時刻均在變化，且磁性液體的粘度對流體的運動有很大影響，而粘度在磁場下是變化的，因此建立微壓差傳感器強耦合模型，將更符合實際的情況。

假定磁性液體為牛頓流體，基于經典流體動力學理論，單位體積磁性液體在磁場中運動方程的基本形式為：

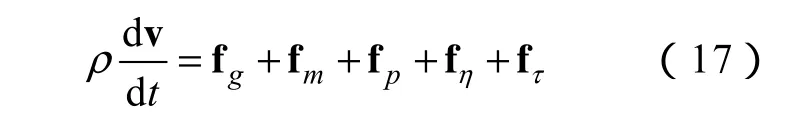
上式右邊各項：

（1）fg為磁性液體的重力，是體積力，表示為

（2）fm是磁場力，即 Kelvin力，是磁性液體特有的由外磁場引起的一種體積力[16]，表示為

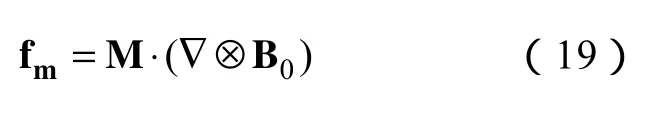
（3）fp是磁性液體受到的壓力梯度，是一種表面力，表示為此處沒有上提一行，麻煩請修改，非常感謝

此處的壓力p僅指外界壓力差ΔP，若從能量的角度考慮，還包括磁性液體在磁場中磁化產生的磁化壓力 pm和在磁場中體積變化引起的磁致伸縮壓力ps，可表示為

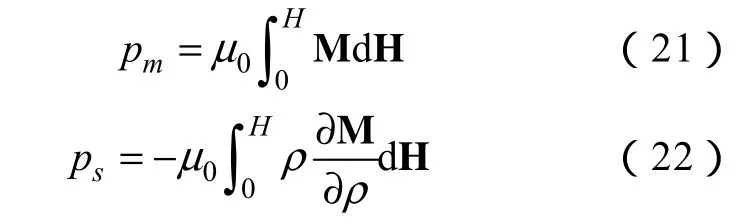
（4）fη是粘性力，表示為

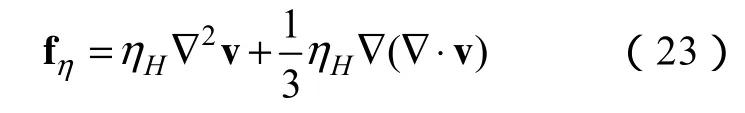
實際中磁場對磁性液體粘度有影響，記為ηH。在微壓差傳感器的模型中，磁性液體的密度ρ為常數，即為不可壓縮流體，即0=??v，則有

（5）fτ是磁性液體內部固相顆粒轉動引起的附加力，即考慮磁性液體為兩相流時，液固兩相渦旋的速度滯后產生的，此時將磁性液體當做均勻相流體對待，該力可認為等于零。

同時磁性液體的磁化強度矢量 M和磁場 H平行，有：

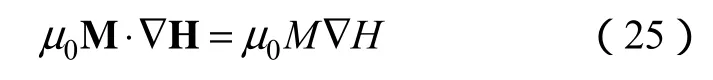
若不考慮磁性液體的磁致伸縮量，有：

磁場H的分布隨著磁性液體的運動而改變，即ηH不為常數，為磁場H的函數，表示為：

綜合式（17）～（27），則微壓差傳感器內磁性液體的動態耦合模型可表述為

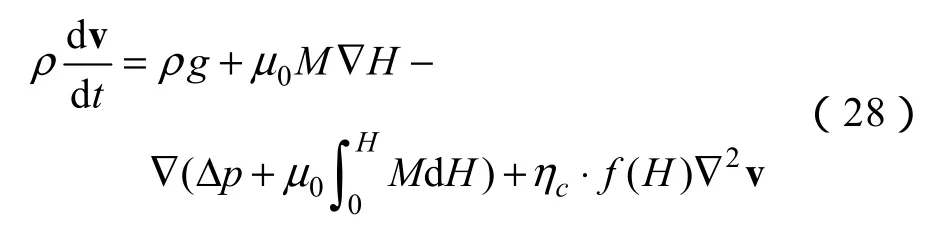
式(28)可看出，外磁場對磁性液體運動的影響表現在ηH上，通常外磁場改變磁性液體粘度對其運動的影響，比磁場力（即Kelvin力）的影響大得多。

4 磁性液體微壓差傳感器模型仿真

利用式（28）對微壓差傳感器進行仿真，模型如圖5所示。

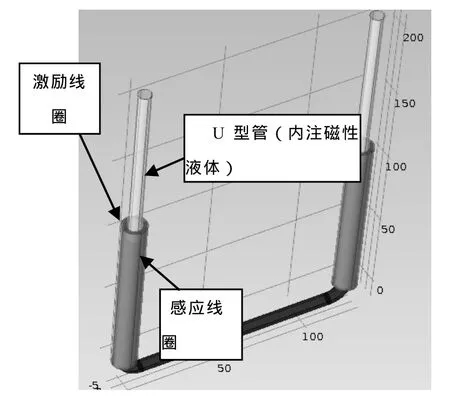
圖5 傳感器三維仿真模型Fig.5 The 3D simulation model of the differential pressure sensor

U形管內磁性液體的界面處于線圈的中間位置，當U形管兩端壓力差為恒定靜壓力，或頻率較低的正弦壓力源（10～50 Hz）時，管內磁性液體的流動為層流。

壓差為恒定壓力時，兩感應線圈的感應電壓差為幅值恒定的正弦波，頻率與激勵源相同。

壓差為正弦壓力時，圖6為兩側液面高度水平集變量對管壁的積分，可看出，該傳感器系統在初始壓力為零的情況下開始加壓，需要50ms左右的滯后過渡，在 0.1s之后，開始逐步跟隨壓力的變化，壓力為正弦變化，液面的變化最終亦表現為正弦，且頻率與壓力源的頻率一致。

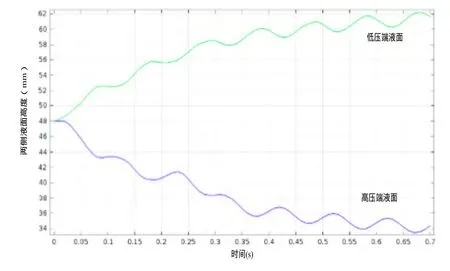
圖6 兩側液面高度Fig.6 The liquid height on both sides

當激勵電源頻率為1000Hz，壓力源頻率10Hz，兩感應線圈的感應電壓差穩定后的波形如圖 7所示，呈幅值為正弦變化的正弦波，波形頻率為激勵源頻率，幅值變化的頻率為正弦壓力源的頻率，即波形的包絡線為雙正弦曲線。

圖7 正弦壓力差時感應電壓差波形Fig.7 Induction voltage difference with sinusoidal pressure difference

圖8中為感應電壓差的上、下包絡線，可看出與壓差源波形一致。圖9為仿真模型的輸入輸出曲線。

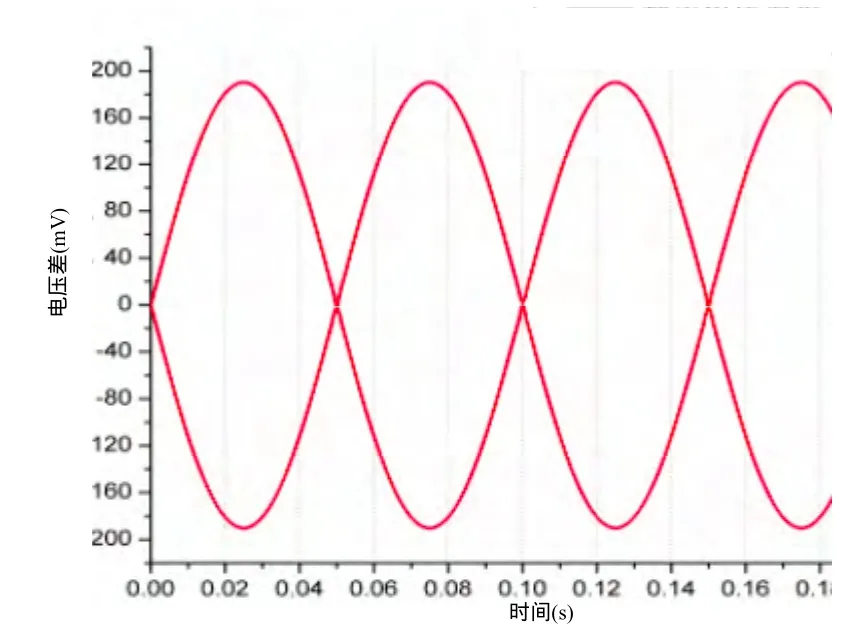
圖8 正弦壓力差時感應電壓差波形包絡線Fig.8 Induction voltage difference envelope with sinusoidal pressure difference

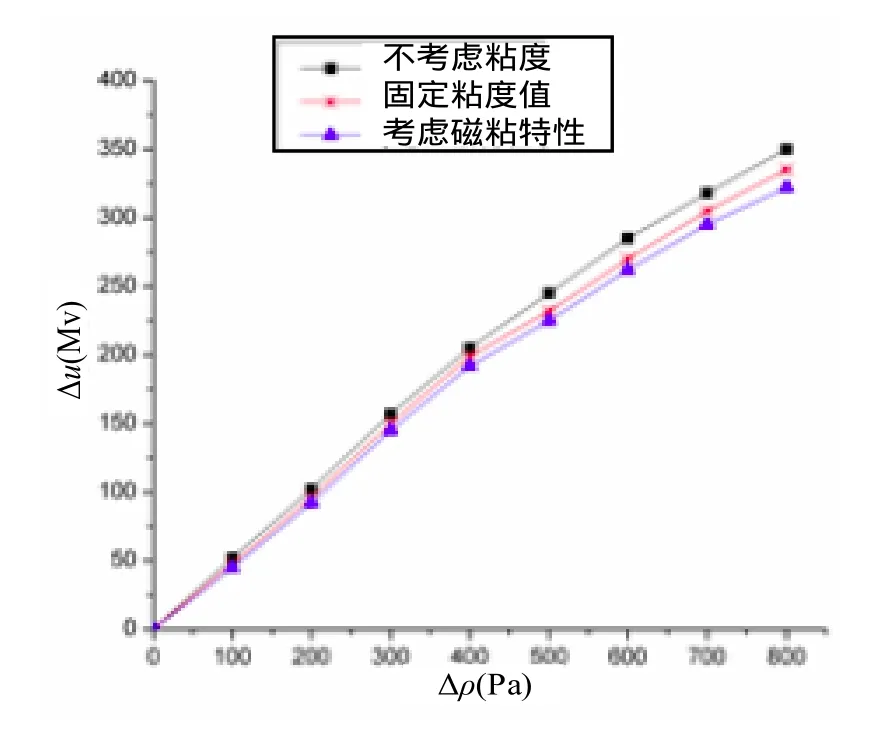
圖9 微壓差傳感器輸入輸出曲線比較Fig.9 The input and output curves of the differential pressure sensor

分析結果可得：

(1)當外加壓差相同時，不考慮粘度影響時得到的輸出電壓差值大于考慮粘度時的電壓輸出；

(2)當輸出電壓相同時，不考慮粘度影響時所對應的壓差值要比考慮粘度時的小；

(3)考慮磁性液體的磁粘特性，相同壓差下，輸出電壓值比考慮粘度為無磁場固定值時的輸出更小，表明磁性液體在磁場下粘度增大，壓力要克服的粘性力變大，位移變小，輸出電壓變小。

上述結論與理論分析是一致的。

5 結論

本文對一種磁性液體微壓差傳感器的基本工作原理進行了分析，并根據流體運動學理論，考慮了磁性液體粘度在磁場中的變化，建立了傳感器磁場—流體場耦合模型。利用該模型進行了傳感器動態特性的仿真，結果與理論推導值具有一致性。該模型為研究磁性液體微壓差傳感器的動態特性、優化傳感器結構、提高傳感器精度提供了理論依據和技術支持。尋找適合的正弦低頻微壓力源，對微壓差傳感器施壓正弦壓力，進行頻域動態實驗，將進一步驗證動態模型的正確性。

[1] 池長青.鐵磁流體的物理學基礎和應用[M].北京:北京航空航天大學出版社,2011.

[2] 李德才.磁性液體理論及應用[M].北京:科學出版社,2003.

[3] Ilg P,Odenbach S.Ferrofluid structure and rheology[J].Lecture Notesin Physics.2009,763:249-325.

[4] Nowak J,Odenbach S.Magnetoviscous effect in a biocompatible ferrofluid[J].IEEE Transactions on Magnetics.2013,49(1):208-212.

[5] 郝瑞參.磁性液體微壓差傳感器的理論及實驗研究[D].北京交通大學,2011.

[6] 郝瑞參,李德才.差動式磁性液體微壓差傳感器數學模型計算及試驗驗證[J].機械工程學報.2010,46(12):161-165.

Hao Ruican,Li Decai.Mathematic model and experiment of pressure difference sensor with magnetic fluid[J].Journal of Mechanical Engineering,2010,46(12):161-165.

[7] Jianhua Li,Rong Wang,Jingyuan Wang.Novel magnetic field sensor based on magnetic fluids infiltrated dual-core photonic crystal fibers[J].Optical Fiber Technology:Materials,Devices and Systems,2014,20(2):100-105.

[8] N.C.PoPa,A.Siblini,L.Jorat.Aspects concerning the dimensioning of the inductive transducers with magnetic fluids[J].Journal of Magnetism and Magnetic Materials,2002(242-245):1240-1242.

[9] B.Ando,A.Ascia,S.Baglio.A ferrofluidic inclinometer in the resonant configuration[J].IEEE Transactions on Instrumentation and Measurement,2010,59(3):558-564.

[10] G.Chitnis,B.Ziaie.A ferrofluid-based wireless pressure sensor[J].Journal of Micromechanics and Microengineering,2013,23(12):125031(6pp).

[11] B.Ando,S.Baglio,A.Beninato.A flow sensor exploiting magnetic fluids[J].Procedia Engineering,2011,25:559-562.

[12] W.Yang,Q.Yang,C.Fan，et al.Dynamic analysis and experiment on magnetic fluid acceleration sensor[J].International Journal of Applied Electromagnetics and Mechanics,2007,15(3):250-253.

[13] W.Yang,Q.Yang,W.Zhang.Dynamic response of pressure sensor with magnetic liquids[J].IEEE Transactions on Applied Superconductivity,2010,20:1860-1863.

[14] 顏威利,楊慶新,汪友華.電氣工程電磁場數值分析[M].北京:機械工業出版社,2005.

[15] Rosensweig R E.Ferrohydrodynamics[M].Cambridge University Press,1985.

[16] 劉桂雄,蒲堯萍,徐晨.磁流體中Helmholtz和Kelvin力的界定[J].物理學報,2008,57(4):2500- 2502.

Liu Guixiong,Pu Yaoping,Xu Chen.Definition of helmholtz and kelvin forces in magnetic fluids[J].Acta Physica Sinica,2008,57(4):2500-2502.