二階傳輸條件撕裂互連法在電大輻射中的應用
孔才智+郝毫保


摘 要: 針對于大尺寸電磁輻射問題,將撕裂互連法應用于三維電大尺寸輻射問題的計算仿真。該算法是區域分解方法中的一種,求解區域劃分成互不重疊的子區域,各子區域之間通過拉格朗日乘子將交界面的連續邊界條件或者傳輸條件耦合。鑒于原來的傳輸條件存在不收斂或者收斂較慢情況,提出同時能在TE/TM凋落模式快速收斂的二階傳輸邊界條件作為子區域之間交界面的邊界條件,并且引入虛擬激勵流為交換信息。數值結果表明,該改進算法有效地提高了撕裂互連法在迭代求解中的收斂性。在求解三維電大輻射問題時,該算法仿真結果與有限元算法結果一致,表明撕裂互連算法是計算大尺寸電磁輻射問題的一種有效方法。
關鍵詞: 撕裂互連法; 有限元法; 二階傳輸邊界條件; 電磁輻射
中圖分類號: TN911?34; O441 文獻標識碼: A 文章編號: 1004?373X(2015)16?0004?05
Application of tearing and interconnecting method in large?scale electromagnetic radiation under second?order transmission conditions problem
KONG Caizhi, HAO Haobao
(South China Normal University, Guangzhou 510006, China)
Abstract: The tearing and interconnecting method is applied to the simulation of three?dimensional (3?D) large?scale electromagnetic radiation to solve the problems of large?scale electromagnetic radiation. As one of the domain decomposition methods, this method reduces the computational complexity by dividing the domain under solution into several non?overlapping subdomains. The continuous boundary conditions or transmission conditions of the sub?domain interfaces are coupled by using the Lagrange multipliers and an iterative process is used to realize the solution of the original global problem. For further increasing the convergence of this method, a second?order transmission condition that can transmit both TE and TM evanescent modes is developed A virtual excitation source is introduced as the exchange information. Numerical simulation results reveal that the modification has improved effectively convergence performance in the iteration solution of the tearing and interconnecting method. Regarding to the electromagnetic radiation problems, the results are well matched with those obtained by finite element method.
Keywords: tearing and interconnecting method; finite element method; second?order transmission condition; electromagnetic radiation
0 引 言
傳統的有限元方法在處理電大尺寸輻射問題和復雜細節結構目標上出現未知數的數量很多,導致全局線性系統矩陣規模龐大,矩陣形態較差,迭代求解往往很慢甚至不收斂。區域分解法提出在并行計算上的優勢,是有限元方法解決這些問題的重要方法之一。在眾多區域分解算法當中,撕裂互連法被證明是非常有前景和高效的算法之一[1?3]。該算法將原求解區域劃分成若干個不重疊的子區域,在子區域的交界面上使用拉格朗日乘子隱式強加場的連續性條件把子區域連接起來,通過消去法將全局未知量的矩陣變成子區域交界面未知量的系統矩陣,一旦獲得交界面上的未知量,代回到相應的子區域,各子區域就可以單獨求解。撕裂互連算法不僅具有區域分解法的“分而治之”的策略優點,而且減少全局未知量為交界面的未知量,使其系統矩陣應用Krylov子空間迭代求解[4?5],避免了求解大矩陣的復雜問題。為了提高算法在高頻電磁中的迭代收斂性,實現子區域交界面的一階Robin類型傳輸條件(FOTC)替代連續性條件耦合,并將該算法應用到三維電大尺寸電磁問題上,模型用一階吸收邊界條件或者完全匹配層(PML)截斷求解區域[6?8]。由于一階傳輸條件(FOTC)只能用于傳輸模式,為了能夠傳輸TE的凋落模式和提高迭代算法的收斂性,在子區域之間的交界面引入二階傳輸條件(SOTC?TE)求解大規模多區域的電磁模型[9?10]。具體的計算實例表明,二階傳輸條件具有更高的收斂效果。
為了達到提高算法精度和分析復雜結構的目標,網格剖分變密,導致分界面的單元中存在凋落模式,凋落模式會嚴重影響到傳輸條件的收斂模式,上述提到的二階傳輸條件(SOTC?TE)僅能在TE模式下快速收斂。本文將推導出適用于撕裂互連法新型的SOTC?FULL二階傳輸條件,使得該傳輸條件具備更明顯的物理意義,該傳輸條件能同時在TE和TM凋落模式下快速收斂。將改進后的算法應用于求解三維電磁輻射問題中,采用一階吸收邊界條件截斷求解區域。
1 撕裂互連原理與傳輸條件
一個有截斷邊界的有源電磁問題可以歸結為在[Ω]空間上求解邊值問題的矢量波動方程。不失一般性,將求解自由空間劃分為互不重疊的子空間。每個子空間內建立有限元矢量波動方程以及限定的邊界條件:
在[Ωs]子空間內滿足:
[?×μ-1r?×E-k2oεrE=-jkozoJimp] (1)
在PEC邊界滿足的邊界條件:
[n×E=0] (2)
在PMC邊界滿足的邊界條件:
[n×?×E=0] (3)
一階吸收邊界條件(ABC):
[n×(?×E)+jkin×(n×E)=Uinc] (4)
其中:[Ωs]表示第[s]子空間;[ko]和[zo]分別為自由空間的波數和波阻抗;[Jimp]為內部強加源;PEC為理想導體邊界條件;PMC為理想磁場邊界條件;[Uinc=][n×(?×Einc)+jkin×(n×Einc)]為入射波,[ki=koμrεr]。
當一個原求解區域劃分為若干個子區域,只要保證子區域之間場的連續性,則由子區域與子區域之間的傳輸條件所構成的問題與原問題等效,這是區域分解法的基本思想。撕裂互連法是將拉格朗日乘子引入到傳輸條件中,最初的算法是用Dirichlet邊界連續性條件表示傳輸條件,由于在該條件下存在無法收斂或者收斂很慢的情況,因此引用Robin一階傳輸條件;進一步應用發現,當網格劃分變密,頻率變低時[11?12],分界面單元中將存在凋落模式,該模式影響傳輸條件的收斂效果。為了改善收斂效果,本文引入非共形區域分解法(Non?conformal Domain Decomposition Method)[13?15]中能同時在TE和TM凋落模式下快速收斂的二階傳輸條件(SOTC?FULL),推導出使該方法適用于撕裂互連算法的形式,表示如下:
[ni×(μ-1ri?×Ei)+αini×(ni×Ei)-βi?× [ni(?×Ei)n]+γi?τ?τ·[ni×(μ-1ri?×Ei)]=Λ] (5)
式中:[i]表示子區域之間的界面;[αi=jkoμsqrεsqr],[μsqr]和[εsqr]分別表示子區域界面兩邊的相對介電常數和磁導率的均值;[βi]和[γi]由最小網格和基函數的階數決定,[βi=-j(k+ktez)],[γi=1(k2+kktmz)],在這里取[kmax,ter=πhmin],[kmax,tmr=π/(2×hmin)],[hmin]是子區域界面的最小網格尺寸,若[βi=0],[γi=0],則式(5)為一階傳輸條件FOTC,若[γi=0],式(5)變為SOTC?TE傳輸條件,[Λ]為子區域界面引入的拉格朗日乘子未知量。
基于上述邊界條件的基礎,本文推導出一種新型的二階傳輸條件,對于式(5)中的第4項[γi?τ?τ·[ni×(μ-1ri?×Ei)]],因為[ni×(μ-1ri?×Ei)]只有切向分量,所以:
[?τ·[n×(μ-1r?×E)]=(?-?n)·[n×(μ-1r?×E)] =[?·[n×(μr-1?×E)]]]
根據矢量恒等式和在自由空間的無源二階矢量波動方程得到:
[?·[n×(μ-1?×E)]=n·[?×(μ-1?×E)]=k2oεrn·E]
將式(5)中的傳輸條件展開分別表示為交界面2個不同子區域的傳輸條件,把分界面上的傳輸條件看成是一種激勵,本文中以[gi]來表示,這一激勵類似于面電流。因此式(5)可以分解為以下2種形式:
[ni1×(μ-1ri1?×Ei1)+αi1ni1×(ni1×Ei1)-βi1?× [ni1(?×Ei1)n]+γi1?τn·E=gi] (6)
[-ni2×(μ-1ri2?×Ei2)+αi2ni2×(ni2×Ei2)-βi2?× [ni2(?×Ei2)n]-γi2?τn·E=gi] (7)
式中:[i1]表示[Si∈Ω1];[i2]表示[Si∈Ω2]。
對于子區域[Ωs]聯立方程式(1)~式(4),式(6),式(7),將子區域矢量場用矢量棱邊元展開,并運用伽遼金方法,獲得子區域的矩陣方程:
[Ks{Εs}={fs}-i∈neibourΩssiNs·gids] (8)
式中:s表示子區域編號;[Εs]為待求的電場未知量;子區域有限元矩陣[Ks]和激勵向量[fs]的具體形式如下:
[Ks=Ω[μ-1r(?×Ns)·(?×Ns)-k2oεrNs·Ns]dv+ jkoSABC(n×Ns)·(n×Ns)ds+αs(n×Ns)·(n×Ns)ds+ βs(?×Ns)n(?×Ns)nds+γs(n·Ns)(?τ·Ns)ds] (9)
[{fs}=-jkozoΩNs·Jimpdv-SABCNs·Uincds] (10)
每個子區域中的單元邊未知量按照位置可以分為3種類型[E=[Ev,Ei,Ec]],分別表示內部棱邊,交界面和拐角處未知量,其中[Ev,Ei]可以歸為一類[Er]。因此子區域的矩陣有限元系統可以表示為:
[Ks=KsrrKsrcKscrKscc, {Εs}=ΕsrΕsc] (11)
交界面[Si]上定義與交界面相關的矢量[ρi]以及布爾矩陣[Bi]。假定某一棱邊在子區域[Ωi]和子區域[Ωj]的交界面[Si]上的編號[p],在子區域內[Ωi]的編號為[q],在子區域[Ωj]的編號為[t],則[BTi(p,q)=1],[BTj(p,t)=1],因此:
[BTiρi=-BTjρi=siNs·gids] (12)
將所有的拐角(多個子區域重疊的邊)處的棱邊進行編號,并定義布爾矩陣[Bsc]為棱邊對應在拐角上的編號與子區域內部編號的映射關系矩陣。假定在子區域內[Ωs]內某一拐角的編號為[m],在全局拐角棱邊編號為[n],則[Bsc(m,n)=1],用[Ec]表示全局拐角未知量:
[BscEc=Esc] (13)
聯立式(8),式(11)~式(13),在子區域[Ωs]內矩陣形式可表示為:
[KsrrKsrcKscrKsccΕsrΕsc=fsrfsc--Biρi+Bjρi 0] (14)
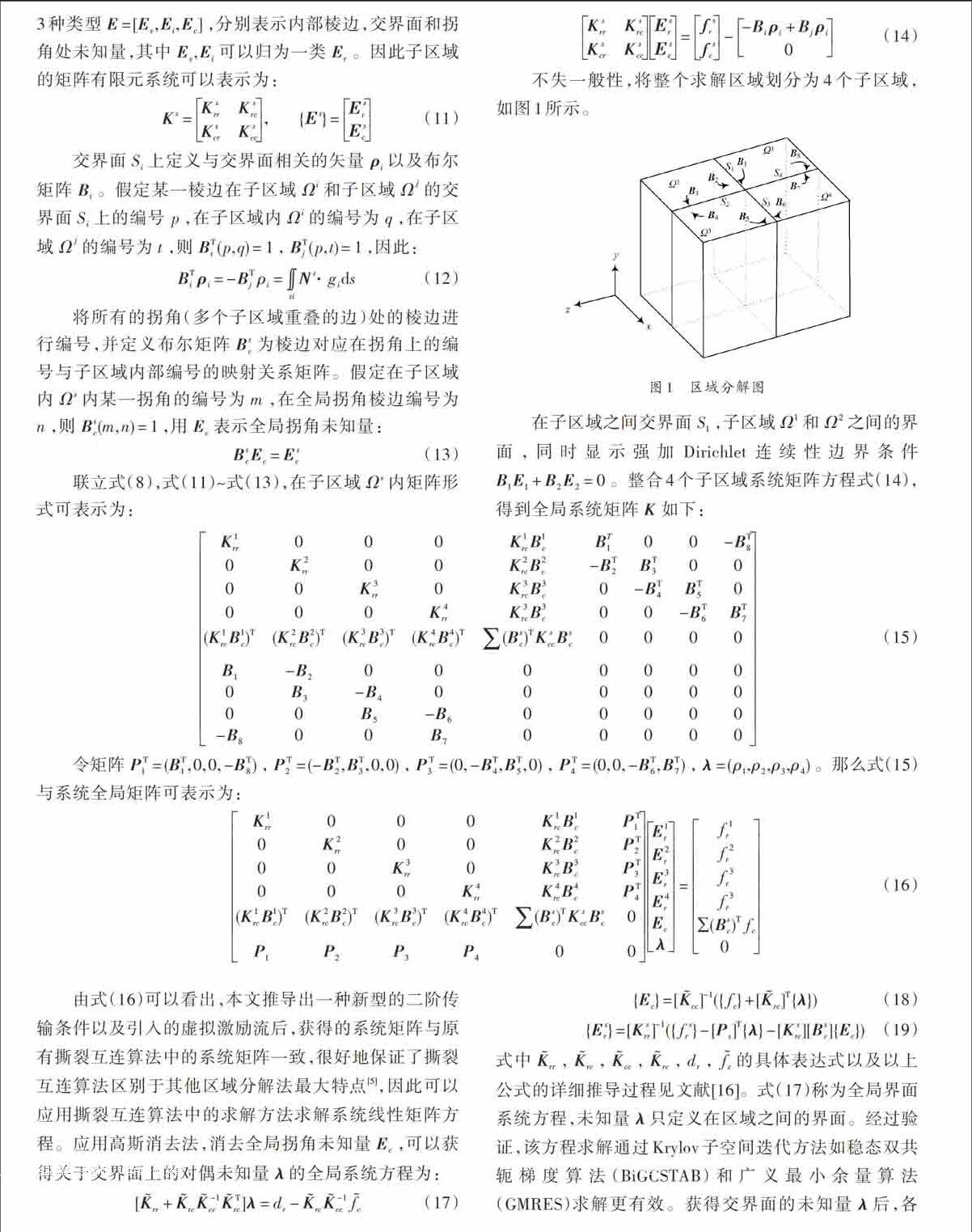
不失一般性,將整個求解區域劃分為4個子區域,如圖1所示。
圖1 區域分解圖
在子區域之間交界面[S1],子區域[Ω1]和[Ω2]之間的界面,同時顯示強加Dirichlet連續性邊界條件[B1E1+B2E2=0]。整合4個子區域系統矩陣方程式(14),得到全局系統矩陣[K]如下:
由式(16)可以看出,本文推導出一種新型的二階傳輸條件以及引入的虛擬激勵流后,獲得的系統矩陣與原有撕裂互連算法中的系統矩陣一致,很好地保證了撕裂互連算法區別于其他區域分解法最大特點[5],因此可以應用撕裂互連算法中的求解方法求解系統線性矩陣方程。應用高斯消去法,消去全局拐角未知量[Ec],可以獲得關于交界面上的對偶未知量[λ]的全局系統方程為:
[[Krr+KrcK-1ccKTrc]λ=dr-KrcK-1ccfc] (17)
[{Ec}=[Kcc]-1({fc}+[Krc]T{λ})] (18)
[{Esr}=[Ksrr]-1({fsr}-[Ps]T{λ}-[Ksrc][Bsc]{Ec})] (19)
式中[Krr],[Krc],[Kcc],[Krc],[dr],[fc]的具體表達式以及以上公式的詳細推導過程見文獻[16]。式(17)稱為全局界面系統方程,未知量[λ]只定義在區域之間的界面。經過驗證,該方程求解通過Krylov子空間迭代方法如穩態雙共軛梯度算法(BiGCSTAB)和廣義最小余量算法(GMRES)求解更有效。獲得交界面的未知量[λ]后,各個子域內部的電場值可以通過子域方程式(18),式(19)分別求出。原來三維有限元方程問題轉化為二維界面問題,交界面上的未知量通常比較少,因此求解該方程的維度和計算量比原有限元系統方程減少很多,所以該方法能夠求解電大電磁輻射和散射問題。
2 數值算例
算例1:為了驗證撕裂互連法在不同的傳輸條件FOTC,SOTC?TE,SOTC?FULL下的收斂性和算法的正確性,仿真了自由空間波傳播的算例,如圖2所示。
圖2 自由空間波傳播求解區域
該模型內外都是空氣,入射波[E=xe-jkz+ye-jkz],入射波沿Z軸傳播的與X軸成45°極化方向的平面波。求解空間用一階吸收邊界條件截斷外邊界,整體求解區域剖分為4個子區域,網格劃分密度為[λ20],入射波頻率為10 GHz,收斂精度為[10-8],采用完全相同的網格剖分和子區域劃分方式,全局具有2 240個未知量。從圖3迭代結果可以看出SOTC?FULL的收斂速度比FOTC,SOTC?TE傳輸條件的收斂效果好。
圖3 自由空間波傳播模型不同傳輸條件迭代結果對比圖
算例2:因為撕裂互連法適用于大尺寸電磁分析特別是天線有限陣列,因為在多數典型的天線陣列中,很多天線單元是相同的。對天線陣列進行仿真,只要構造和計算幾個子區域的有限元矩陣。整個求解區域劃分為9個子區域,如圖4所示。
圖4 具有不同有限元矩陣的9個子區域圖
由于應用外邊界如吸收邊界條件和完全匹配層,邊和角的有限元矩陣不同于內部的有限元矩陣,為此,其他的有限元矩陣可由這9個矩陣確定下來。也就是說,這9個子區域的有限元矩陣[Ksrr]一旦構成和計算出來,這些矩陣可以在全局系統界面方程迭代過程和最后的各個子區域求解過程中替代其他子區域矩陣。
本文應用撕裂對接算法仿真和分析微帶饋電的貼片天線,如圖5所示。
圖5 微帶饋電貼片天線結構圖
16 mm
圖6給出了撕裂互連算法求解該模型的S11參數結果圖,文章中的算法計算結果和ANSYS求解的結果吻合的非常好。
圖6 貼片天線的S11參數算法仿真與ANSYS仿真結果對比圖
3 結 語
本文推導和提出適用于撕裂互連算法的二階傳輸條件(SOTC?FULL),并簡要介紹了其公式推導過程。驗證了該二階傳輸條件(SOTC?FULL)比一階傳輸條件(FOTC)有更好的收斂性,并且將其應用到撕裂互連算法求解電磁輻射問題上分析微帶饋電貼片天線。仿真結果與ANSYS軟件中的求解結果符合程度高,從而證明了撕裂互連算法是計算大尺寸電磁輻射問題的一種有效方法。
參考文獻
[1] LI Y, JIN J M. A vector dual?primal finite element tearing and interconnecting method for solving 3?D large?scale electromagnetic problems [J]. IEEE Transactions on Antennas and Propagation, 2006, 54(10): 3000?3009.
[2] LI Y J, JIN J M. A new dual?primal domain decomposition approach for finite element simulation of 3?D large?scale electromagnetic problems [J]. IEEE Transactions on Antennas and Propagation, 2007, 55(10): 2803?2810.
[3] 杜磊.時域有限元電磁計算方法的研究[D].南京:南京理工大學,2010.
[4] ZHAO Kezhong. A domain decomposition method for solving electrically large electromagnetic problems [D]. Ohio State: The Ohio State University, 2007.
[5] JIN J M, RILEY D J. Finite element analysis of antennas and arrays[M]. John Wiley & Sons, 2009. 336?387.
[6] 賈會亮.頻域有限元區域分解法的研究[D].南京:南京理工大學,2009.
[7] XUE M F, JIN J M. Nonconformal FETI?DP methods for large?scale electromagnetic simulation [J]. IEEE Transactions on Antennas and Propagation, 2012, 60(9): 4291?4305.
[8] 高紅偉,盛新慶.三維非均勻電大目標散射的有限元撕接區域分解法計算[J].北京理工大學學報,2012,32(6):602?606.
[9] PENG Zhen, RAWAT Vineet, LEE Jin?Fa. One way domain decomposition method with second order transmission conditions for solving electromagnetic wave problesms [J]. Journal of Computational Physics, 2010, 229: 1181?1197.
[10] XUE M F, JIN J M. A hybrid conformal/nonconformal domain decomposition method for multi?region electromagnetic modeling[J]. IEEE Transactions on Antennas and Propagation, 2014, 62: 2009?2021.
[11] 馬金.非均勻介質中低頻近場的分析與探測應用[D].成都:電子科技大學,2013.
[12] YAO W, JIN J M, KREIN P T. Application of the LU recombination method to the FETI?DP method for solving low?frequency multiscale electromagnetic problems [J]. IEEE Transactions on Magnetics, 2013, 49(10): 5346?5355.
[13] PENG Z, LEE J F. Non?conformal domain decomposition method with mixed true second order transmission condition for solving large finite antenna arrays [J]. IEEE Transactions on Antennas and Propagation, 2011, 59(5): 1638?1651.
[14] PENG Z, LEE J F. A scalable nonoverlapping and nonconformal domain decomposition method for solving time?harmonic maxwell equations in R^3 [J]. SIAM Journal on Scientific Computing, 2012, 34(3): A1266?A1295.
[15] MA J, NIE Z, SUN X. Efficient modeling of large?scale electromagnetic well?logging problems using an improved nonconformal FEM?DDM [J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(3): 1825?1833.
[16] YAO W. Accurate, efficient, and stable domain decomposition methods for analysis of electromechanical problems [D]. Urbana: University of Illinois at Urbana?Champaign, 2014.

