響應率法求解二階部分極點配置問題

陳梅香

（華僑大學 數學科學學院，福建 泉州362021）

1 預備知識

二階控制系統為

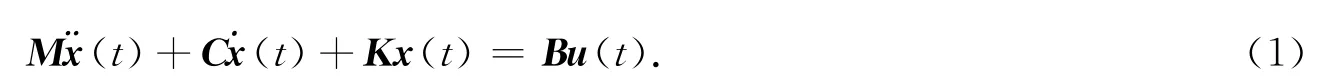
式（1）中：正定矩陣M∈Rn×n為質量矩陣；半正定矩陣C∈Rn×n為阻尼矩陣；半正定K∈Rn×n為剛度矩陣；B∈Rn×m為輸入矩陣；關于時間t的n維向量x（t）和u（t）分別為狀態向量和控制向量.取

式（2）中：F∈Rn×m，G∈Rn×m稱為反饋矩陣；FT表示矩陣F的轉置.若有

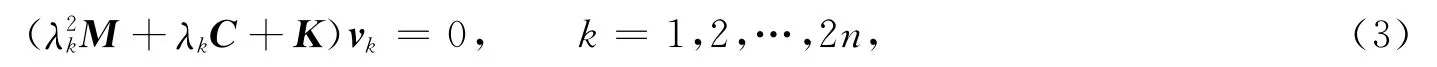
則稱（λk，vk）為開環系統P（λ）＝λ2M＋λC＋K的特征對.式（3）中：λk稱為特征值；vk稱為特征向量.若有

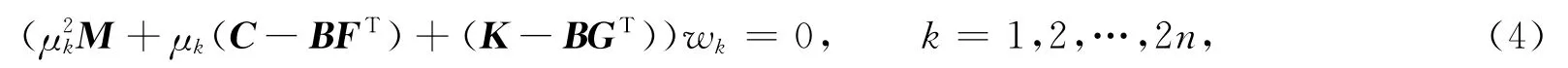
則稱（μk，wk）為閉環系統Pc（λ）＝λ2M＋λ（C－BFT）＋（K－BGT）的特征對.

部分極點配置問題就是給定p個數μ1，…，μp，求得反饋矩陣F∈Rn×m，G∈Rn×m，使得μ1，…，μp將開環系統的p個特征值λ1，…，λp替換，成為Pc（λ）的特征值.而Pc（λ）剩余的2n－p對特征對滿足

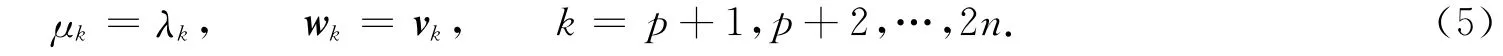
式（5）中：（λk，vk）為開環系統P（λ）的特征對，即開環系統剩余的2n－p對特征對仍為閉環系統的特征對，也把它稱為保持無溢出性.

當m＞1，系統為多輸入系統時，反饋矩陣F和G的解不唯一［1－8］.因此，可以選取使反饋矩陣的范數為最小的解.其中：‖·‖指矩陣的Frobenius范數，將它稱為最小范數的部分極點配置問題.這種情況下得到的閉環系統可以盡量的減少能量的消耗及噪聲的影響.

目前，已有不少求解最小范數的部分極點配置問題的數值方法［1－2］，都需要用到系統的矩陣M，C，K.但是在實際應用中，可能已從實驗中測量得到系統的響應率，即

而系統的矩陣M，C，K是未知的.Ram等［8］提出只需利用響應率求解部分極點配置問題，但其求出的F和G的解不唯一.因此，本文提出一種只需利用響應率求解最小范數的部分極點配置問題的數值方法.

2 定理及其證明

假設｛μ1，…，μp｝∩｛λ1，…，λ2n｝＝?，｛λ1，…，λp｝∩｛λp＋1，…，λ2n｝＝?.控制矩陣B是列滿秩的，而且（P（λ），B）對于λ1，…，λp是部分可控的，即

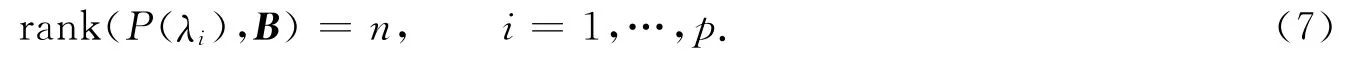
對于所討論的部分極點配置問題，先給出定理1.

定理1設（λk，vk）為開環系統P（λ）的特征對，（μk，wk）為閉環系統Pc（λ）的特征對，若式（5）成立，即μk＝λk，wk＝vk.則

證明 （μk，wk）為閉環系統Pc（λ）的特征對，且μk＝λk，wk＝vk，故有

移項得

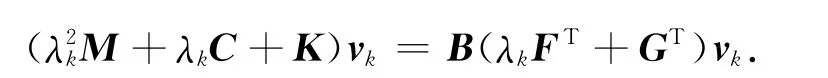
又（λk，vk）為開環系統P（λ）的特征對，即

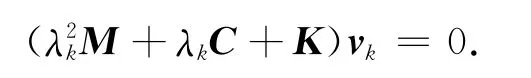
因此，

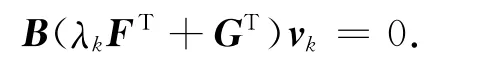
因為是B列滿秩的，故有

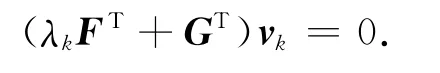
即

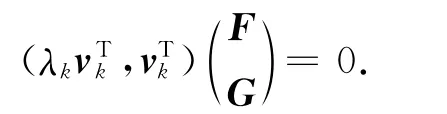
另外，由文獻［1］有定理2.

定理2給定矩陣B∈Rn×m，p個自共軛的特征值，若F和G滿足

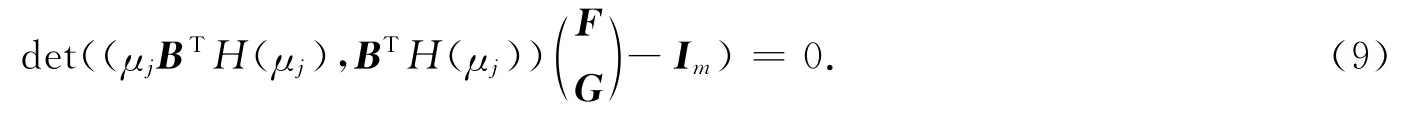
那么，｛μk｝pk＝1為Pc（λ）的p個特征值，即det（Pc（μj））＝0.式（9）中：Im指m×m的單位矩陣.

具體證明見文獻［1］的定理1.

綜合定理1，2，給定p個數μ1，…，μp，矩陣B∈Rn×m，響應率H（μi），i＝1，…，p及開環系統的2np對特征對（λj，vj），j＝p＋1，…，2n.最小范數部分極點配置問題可轉化為關于變量F∈Rn×m，G∈Rn×m的優化問題，即

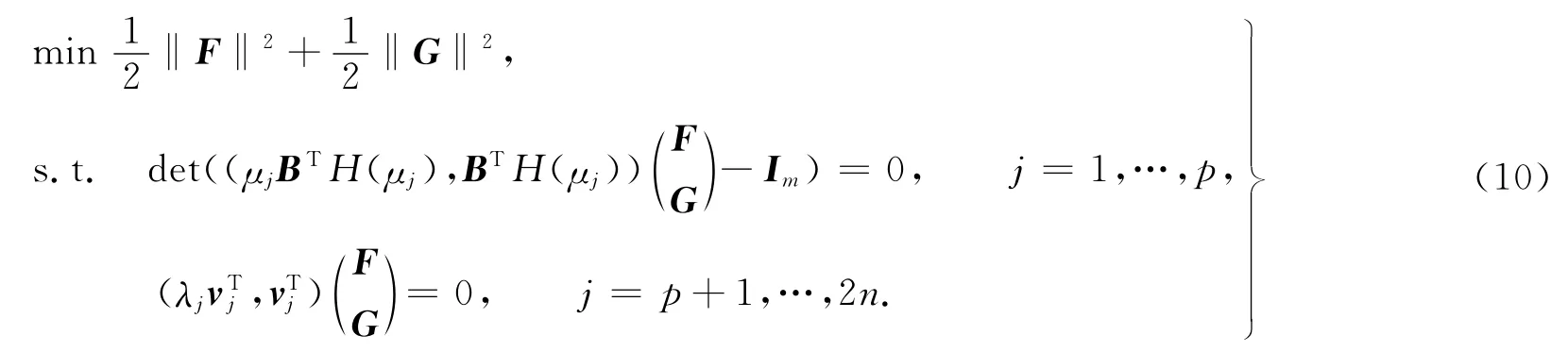
式（11）中：g（Y）＝（g1（Y），…，gp（Y））T；h（Y）＝（h1（Y），…，h2n－p（Y））T.且

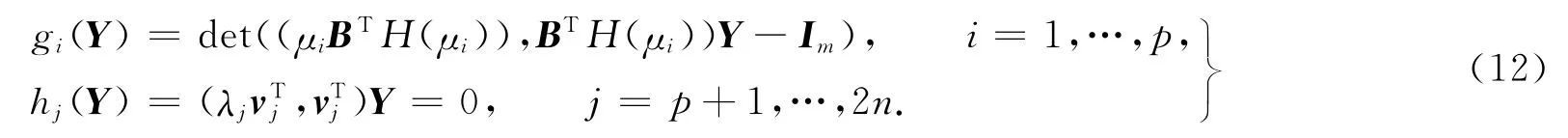
在優化問題（11）中，其目標函數是一個凸函數，滿足約束條件的解的集合是一個凸集.因此，優化問題（11）的KKT條件為求解Y∈C2n×m，ξi∈C，i＝1，…，p，ηj∈Cm，j＝1，…，2n－p，使得

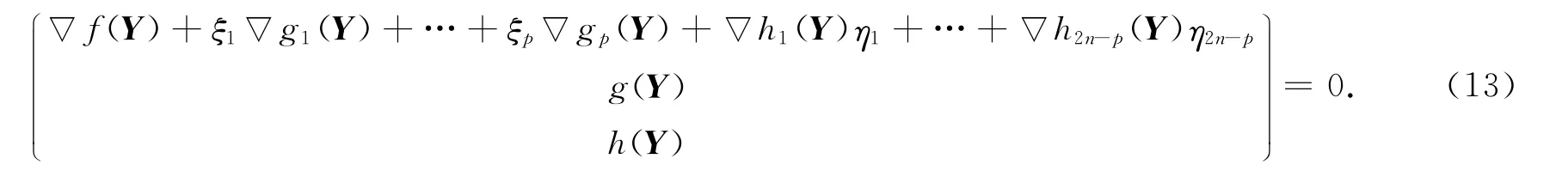
記為F（Y，ξ，η）＝0.其中，

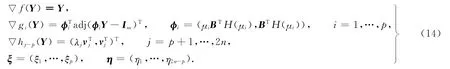
式（14）中：adj（·）表示矩陣的伴隨矩陣.

由此，最小范數部分極點配置問題最終可轉化為求解非線性方程F（Y，ξ，η）＝0.而對于非線性方程F（Y，ξ，η）＝0，可以用經典的Gauss－Newton或trustregion－reflective法［9－10］來求解.

在非線性方程F（Y，ξ，η）＝0中，需要用剩余的2n－p個特征向量.由（λ2jM＋λjC＋K）vj＝H（λj）－1vj＝0可知，2n－p個特征向量可以由響應率H（λj）求解出來，而不需要系統矩陣M，C，K.因此，提出的算法只需利用響應率就可以求解最小范數的部分極點配置問題.

3 數值實驗

為了更直接地呈現所考慮的二階系統，直接給出系統的矩陣M，C，K.但在算法的運行過程中，用的是系統相應的響應率H（λj）.

例1首先考慮文獻［8］中的例子.設

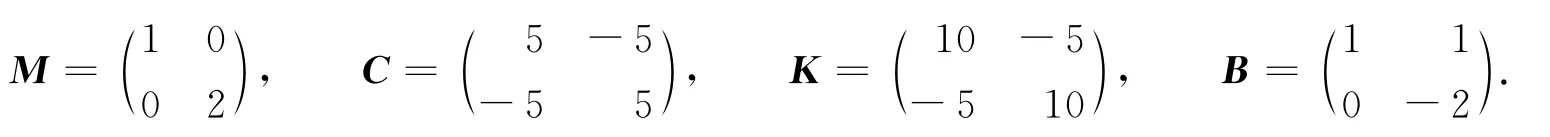
將前p＝2個絕對值最小的自共軛特征值用｛－1±i）替換，其余的特征值保持不變，由提出的算法可得最小范數解為

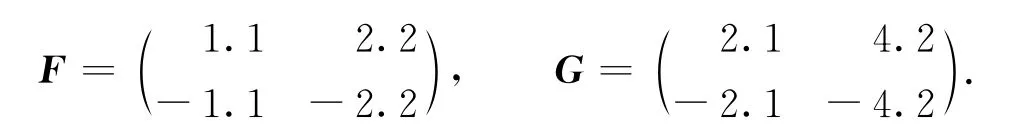
閉環特征值的誤差為

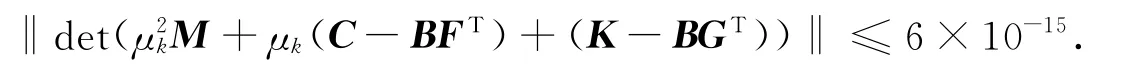
反饋矩陣F和G的范數而在文獻［8］的例2中，得到的反饋矩陣的解為

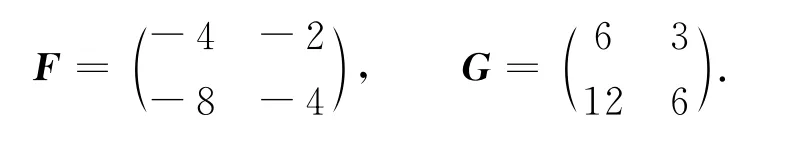
F和G的范數因此，提出的算法所求得的反饋矩陣的范數比文獻［8］的例2中的小得多.

例2將文中的算法與Bai－Chen－Datta［1］的算法進行比較.設

取n＝10，并將前p＝2個絕對值最小的特征值用｛－0.1，－0.2｝替換，而其余的特征值保持不變.由文中的算法得出的解的范數為‖F‖＝1.687 2，‖G‖＝1.078 6，閉環特征值的誤差為

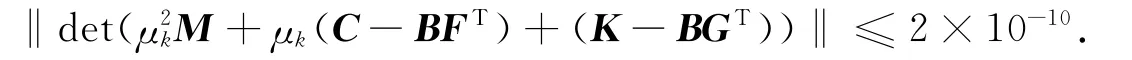
而Bai－Chen－Datta的算法得出的解的范數為‖F‖＝1.410 4，‖G‖＝1.389 1，閉環特征值的誤差為

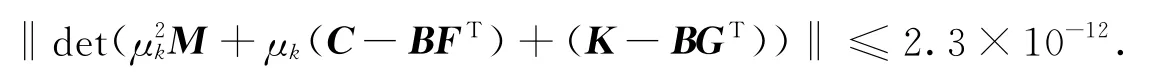
文中的算法與Bai－Chen－Datta的算法相比，所得解的范數差值不大，因此與Bai－Chen－Datta的算法一樣，都能達到取最小范數解的要求.但是，Bai－Chen－Datta的算法需要用到系統矩陣M和K，而文中算法只需用到響應率.

［1］BAI Zheng－jian，CHEN Mei－xiang，DATTA B N.Minimum norm partial quadratic eigenvalue assignment with time delay in vibrating structures using the receptance and the system matrices［J］.Journal of Sound and Vibration，2013，332（4）：780－794.

［2］BAI Zheng－jian，DATTA B N，WANG Jin－wei.Rubust and minimum norm partial quadratic eigenvalue assignment in vibrating systems：A new optimization approach［J］.Mechanical Systems and Signal Processing，2010，24（3）：766－783.

［3］BAI Zheng－jian，CHEN Mei－xiang，YANG Jin－ku.A multi－step hybrid method for multi－input partial quadratic eigenvalue assignment with time delay［J］.Linear Algebra and Its Applications，2012，43（7）：1658－1669.

［4］CHU E K.Pole assignment for second－order systems［J］.Mechanical Systems and Signal Processing，2002，16（1）：39－59.

［5］DATTA B N，ELHAY S，RAM Y M.Orthogonality and partial pole assignment for the symmetric definite quadratic pencil［J］.Linear Algebra and Its Application，1997，257：29－48.

［6］DATTA B N，ELHAY S，RAM Y M，et al.Partial eigenstructure assignment for the quadratic pencil［J］.Journal of Sound and Vibration，2000，230（1）：101－110.

［7］DATTA B N，LIN Wen－wei，WANG J N.Robust partial pole assignment for vibrating structures with aerodynamic effect［J］.IEEE Trans Automatic Control，2006，51（12）：1979－1984.

［8］RAM Y M，MOTTERSHEAD J E.Multiple－input active vibration control by partial pole placement using the method of receptances［J］.Mechanical Systems and Signal Processing，2013，40（2）：727－735.

［9］Jr DENNIS J E.Nonlinear least－squares［C］∥State of the Art in Numerical Analysis.London：Academic Press，1977：269－312.

［10］COLEMAN T F，LI Y.An interior trust region approach for nonlinear minimization subject to bounds［J］.SIAM Journal on Optimization，1996，6（2）：418－445.