土體抗剪強度指標變異水平對邊坡穩定安全系數取值的影響

駱 飛，羅 強，蔣良濰，呂 楊，孔德惠

（1.西南交通大學 土木工程學院；高速鐵路線路工程教育部重點實驗室，成都 610031；2.四川城市職業學院 公共服務系，成都 610110）

邊坡穩定性問題是土木工程領域的一個重要研究內容。傳統邊坡穩定性分析方法以安全系數作為衡量邊坡安全狀態的指標，已在長期的工程實踐中積累了一定經驗，但該方法忽略了土體的物理力學參數所固有的變異性等不確定因素，無法真實全面評價邊坡的安全度［1］。鑒于此，在邊坡穩定性分析中，采用不確定性分析方法以考慮各項不確定因素對邊坡穩定性的影響十分必要。

可靠性分析［2］是一種以概率統計理論為基礎的不確定性分析方法。該方法充分考慮邊坡系統中的不確定性因素，通過計算邊坡的可靠指標β或破壞概率Pf來評價邊坡的穩定性，彌補了傳統的穩定性分析方法僅以經驗性安全系數來表示邊坡穩定狀況的不足，能夠更合理地評價邊坡的安全狀況。可靠性分析在土木工程領域最早被用于評價工程結構的安全狀態，之后發展迅速，目前已在結構工程設計中廣泛應用。相對而言，可靠度理論在邊坡工程中的應用則起步較晚。1970年 Wu等［3］首次將不確定性概念引入到邊坡穩定性分析中，可靠度理論開始應用于邊坡工程。此后，邊坡工程界逐漸從可靠度角度評價邊坡的安全性，進而建立更為完善的邊坡可靠度評價體系。

邊坡工程評價和設計中的數學模型、基本變量及預測結果都包含著許多不確定性因素，大致可分為3類：物理不確定性、統計不確定性和模型不確定性［1］。對此，眾多學者進行了詳細地研究。冷伍明等［4］將土的固有變異性和系統不確定性作為土工參數不確定性的主要來源，引入隨機場理論推導出了土性參數空間變異系數的綜合計算式。張衛民等［5］探討了計算方法、土工參數變異性、地下水位、坡頂荷載等不確定性因素對安全系數取值的影響，對比分析后指出安全系數對土的抗剪強度指標的變異性更為敏感。張繼周等［6－7］系統總結了有關土性參數變異性的研究成果，通過對比分析兩種土層剖面的建模方法，提出了一種基于隨機場理論的土體空間變異性統計方法。羅文強等［8］基于邊坡穩定安全系數的正態分布假設，統計分析了不同中值安全系數及其變異系數下的失效概率，據此建立了一種傳統安全系數與可靠性耦合的邊坡穩定性二元指標體系。黃景華等［9］分析了土性參數中內摩擦角和黏聚力的變異性及其分布形式對邊坡穩定可靠性的影響規律，指出應根據土體抗剪強度指標的變異水平合理選取參數的概率分布形式。對于土體抗剪強度指標變異性對邊坡穩定性的影響這一問題，大多數文獻僅給出了安全系數、可靠指標和失效概率的計算結果，未能系統研究抗剪強度指標的不同變異水平下穩定安全系數與可靠指標之間的相應關系，對安全系數的合理取值研究不夠深入。傳統邊坡穩定性分析方法沿用至今，穩定安全系數取值已在大量的工程實踐中積累了豐富的經驗，而可靠度理論則欠缺相應的工程實踐經驗。掌握穩定安全系數和可靠指標在不同土體抗剪強度指標變異水平下的對應關系，以此優化安全系數的取值對基于可靠性原理的邊坡穩定性設計具有積極指導意義。

為研究土體抗剪強度指標變異水平對邊坡穩定安全系數取值的影響，基于均質路堤邊坡穩定分析模型，運用 Monte－Carlo法［1］進行邊坡穩定可靠性分析。在均值安全系數Fs＝1.25條件下，分析邊坡失效概率隨c、φ變異水平的變化規律，進而指出僅用同一安全系數取值來保證邊坡安全性的不足，建議適當提高容許安全系數的取值；通過設定5個等級的可靠指標，分析其對應的土體抗剪強度指標均值在不同變異水平下安全系數的取值規律，并建立安全系數取值的回歸關系式，對一定可靠指標下穩定安全系數的合理選取進行探討。

1 土工參數不確定性與可靠度計算

1.1 土體抗剪強度指標變異性及水平劃分

土工參數不確定性主要體現在其材料參數的變異性上，變異系數［10］與方差、標準差類似，是反映數據離散程度的特征值，一般用δ表示。

式中：μ是土工參數的平均值；σ是土工參數的標準差，兩者需通過大量且詳細的工程勘察后統計分析得到。變異系數是無量綱量，反映單位均值上的離散程度，可用于比較不同參數之間的離散程度。

與其他工程材料相比，土工材料的各參數指標表現出較大不確定性。近幾十年來，學者們對土工參數變異性進行了大量的研究，其中高大釗［11］、Duncan［12］、張繼周［6］、李小勇［13］等總結了不同試驗方法及不同地域所得部分土工參數的變異系數取值范圍。根據上述資料，表1歸納了影響邊坡穩定性的3個主要土工參數指標（容重、黏聚力、內摩擦角）的變異系數取值范圍。

表1 主要土工參數變異系數取值范圍Table 1 Values range of coefficient of variation for main geotechnical parameters

能否正確選取土工參數變異系數的大小將直接影響邊坡可靠度結果［14］。表1中容重γ的變異系數取值很小，在計算時通常將γ取為定值；c、φ的變異系數取值較大，對邊坡穩定性影響顯著。吳興正［15］統計分析了6條鐵路共13組土樣中土體抗剪強度指標的勘察統計資料，歸納出c、φ的變異系數取值的變化規律，即c、φ的變異系數具有相同的取值趨勢，呈現“同取大同取小”的變化特征。因此，有必要對c、φ的變異系數劃分不同等級進行分析。為研究邊坡穩定安全系數與可靠指標結果隨土體抗剪強度指標變異性的變化規律，根據表1中參數的變異系數取值范圍，將土體抗剪強度指標的變異水平劃分為水平1～5共5種變異水平，具體分級標準見表2。

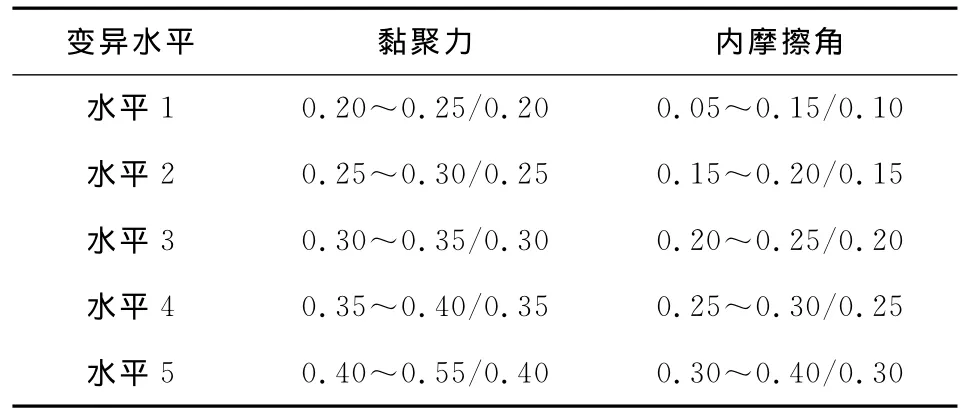
表2 土體抗剪強度指標變異水平劃分Table 2 Grade of coefficient of variation for soil strength indexes

1.2 可靠度計算及邊坡穩定分析

目前，邊坡可靠度分析方法主要有可靠指標法、統計矩法、Monte－Carlo法和隨機有限元法［1］。其中，Monte－Carlo法因原理清晰、操作簡便、運行良好和結果準確而得到廣泛應用。

Monte－Carlo法又稱為隨機模擬或統計試驗法，是一種依據統計抽樣理論，利用計算機研究隨機變量的數值計算方法。該方法計算邊坡可靠度的基本原理［16］為：若已知土工參數隨機變量X1，X2，…，Xn的概率分布和極限狀態方程g（X1，X2，…，Xn）＝1（以邊坡安全系數表達極限狀態），依據隨機變量的分布利用 Monte－Carlo法生成一組隨機數x1，x2，…，xn，將其代入安全系數狀態方程Fs＝g（X1，X2，…，Xn），可得一個安全系數f1，如式（2）所示。

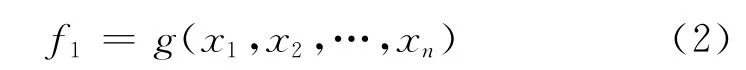
如此重復N次，得到安全系數Fs的一組樣本，樣本容量為N，樣本值為f1，f2，…，fN。若上述N個安全系數中有M 個fi＜1，由Bernoulli大數定理［10］可知，當N足夠大時頻率M／N 的值收斂于邊坡的實際失效概率Pf，則失效概率可用式（3）表示。

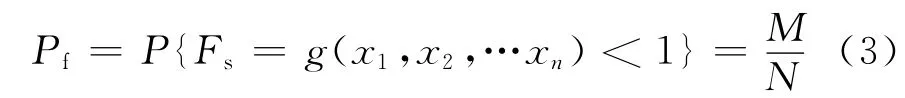
若土工參數隨機變量服從正態分布，上述安全系數Fs的樣本均值為μf，樣本標準差為σf，則可以利用式（4）計算得到工程可靠指標β。

GeoStudio［17］能夠模擬巖土工程、市政、水利和采礦工程中的各種復雜工況，是目前應用最廣泛的巖土工程分析軟件之一。SLOPE／W是GeoStudio的一個重要模塊，可運用Monte－Carlo法分析土工參數的變異性等不確定性因素對邊坡穩定性的影響。SLOPE／W根據用戶輸入的參數平均值、標準差和選用的安全系數計算方法計算出最小安全系數，確定最危險滑面；然后考慮參數變量的不確定性，在已確定的最危險滑面上進行指定次數的Monte－Carlo模擬，得出一組安全系數取值；最后對安全系數進行統計分析得出安全系數平均值ˉFs、最大值Fsmax、最小值Fsmin、標準差σf，計算出邊坡可靠指標β以及失效概率Pf。利用SLOPE／W軟件以及Monte－Carlo法對均質路堤邊坡開展可靠度計算，分析土體抗剪強度指標變異水平對邊坡穩定安全系數取值的影響。

2 邊坡穩定性分析

2.1 邊坡穩定分析模型

邊坡穩定分析模型按照《鐵路路基設計規范》［18］確定土質路堤邊坡模型的幾何尺寸：坡高為8m、坡度為1∶1.5，邊坡與地基的材料相同且為均勻的，如圖1所示。考慮到路堤邊坡的對稱性，采用1／2模型進行計算，安全系數計算方法統一選用鐵路工程技術規范采用的Fellenius法［19］。

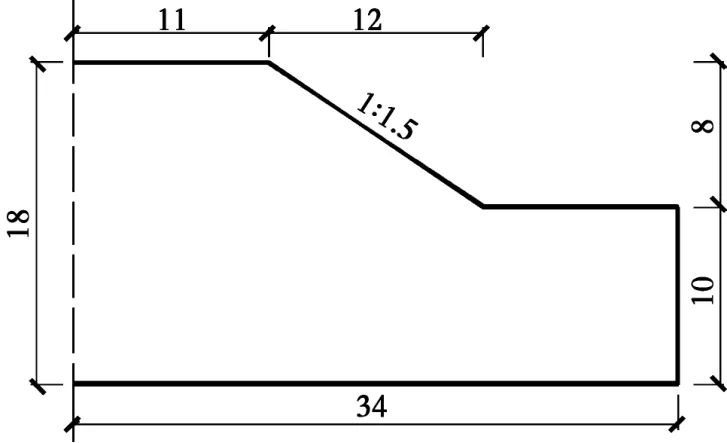
圖1 邊坡穩定分析模型（單位：m）Fig.1 Analysis model of embankment slope（unit：m ）

2.2 土體抗剪強度指標變異性對邊坡可靠指標影響

為分析土體抗剪強度指標變異水平對邊坡可靠指標的影響，將均質路堤邊坡的3個主要土工參數均值取為定值，如表3所列，此時運用SLOPE／W計算出邊坡穩定安全系數Fs＝1.25。

表3 邊坡土工參數均值Table 3 Mean values of geotechnical parameters of embankment slope

考慮均質路堤邊坡土工參數的物理不確定性，分析土體抗剪強度指標處于不同變異水平下可靠指標及失效概率的變化規律。采用SLOPE／W對邊坡進行概率分析，土工參數均值按表3選取，變異水平按表2分級取值，經Monte－Carlo法模擬得到在不同變異水平下的安全系數均值ˉFs、可靠指標β和失效概率Pf如表4所列，繪制失效概率隨抗剪強度指標變異水平變化的統計直方圖如圖2所示。

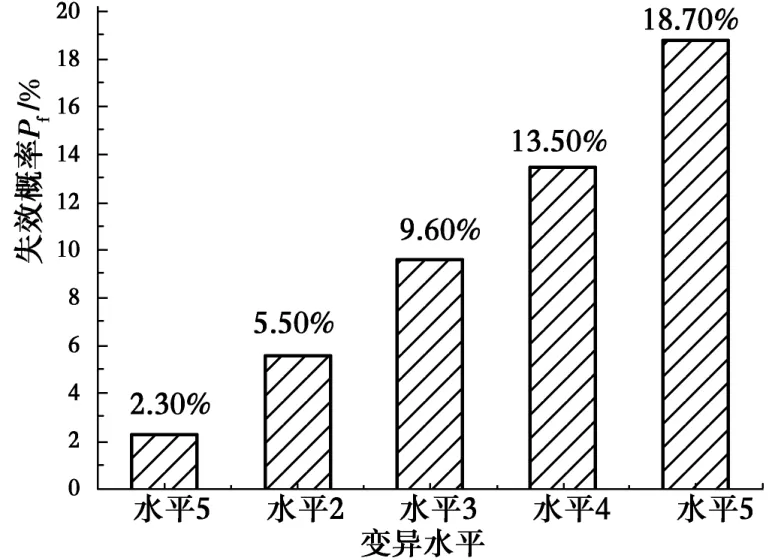
圖2 失效概率計算結果Fig.2 Results for failure possibility

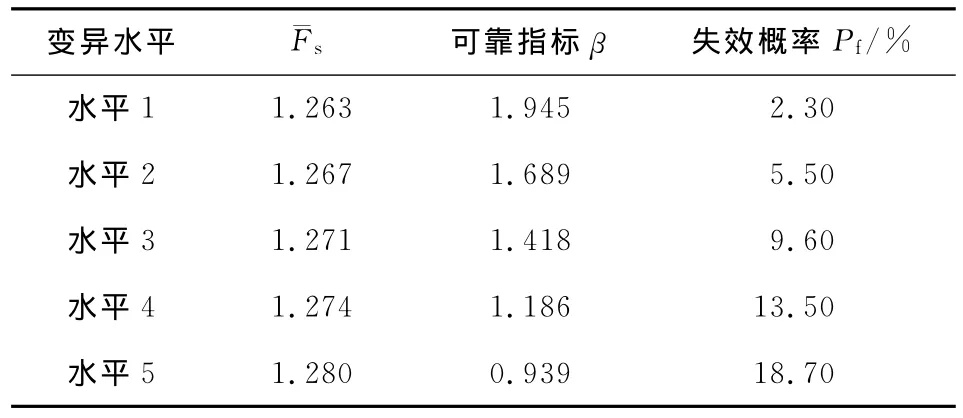
表4 不同變異水平下的計算結果Table 4 Results for different coefficient of variation

計算表明，土體抗剪強度指標變異水平是影響邊坡可靠性的關鍵因素。在同一穩定安全系數條件下，隨著變異水平逐級增大，可靠指標逐漸減小，邊坡失效概率急劇上升，依次從2.4%、5.7%、9.5%、13.6%上升至18.6%。當抗剪強度指標變異水平處于水平3及以上水平時，邊坡安全系數均值與水平1時相比變化并不明顯，而可靠指標和失效概率變化顯著，此時，采用同一安全系數取值來保證路堤邊坡的安全具有較高風險。為保證路堤邊坡具有與線路等級和線路基礎結構相協調的失效概率水平，當土體抗剪強度指標變異水平較大時，要求的設計安全系數應適當增大。

2.3 可靠指標與安全系數關系分析

目前，《鐵路路基設計規范》［17］規定在驗算路堤邊坡穩定性時安全系數不得小于1.25；《鐵路工程地基處理技術規程》［20］對不同列車設計行車速度下路堤邊坡在施工期和運營期的穩定安全系數進行了相應規定，施工期的取值范圍為1.10～1.15，運營期的取值范圍為1.2～1.3（邊坡穩定安全系數驗算均選用Fellenius法）。上述規范均未考慮土體抗剪強度指標變異水平對邊坡穩定安全系數取值的影響，也未對可靠指標與安全系數取值的對應關系進行探討，可能會導致工程實踐中土體抗剪強度指標變異性較大時盲目提高安全系數以保證邊坡安全度的問題。利用可靠指標指導安全系數設計這一思想，通過設定不同的邊坡可靠指標，分析抗剪強度指標在不同變異水平下安全系數取值情況，進而得出均值安全系數取值的變化規律及回歸函數關系式，以此給出容許安全系數取值的相關建議進而指導邊坡可靠性設計。

考慮到土工參數中容重γ的變異性較小，將其取為定值γ＝20kN／m3，分析不同可靠指標下黏聚力c和內摩擦角φ的取值情況及其在不同變異水平下均值安全系數Fs與安全系數均值ˉFs的取值規律。c、φ的變異水平分5個等級參照表2選取，表5所列為5個可靠指標等級條件下c、φ取值及其安全系數計算結果。

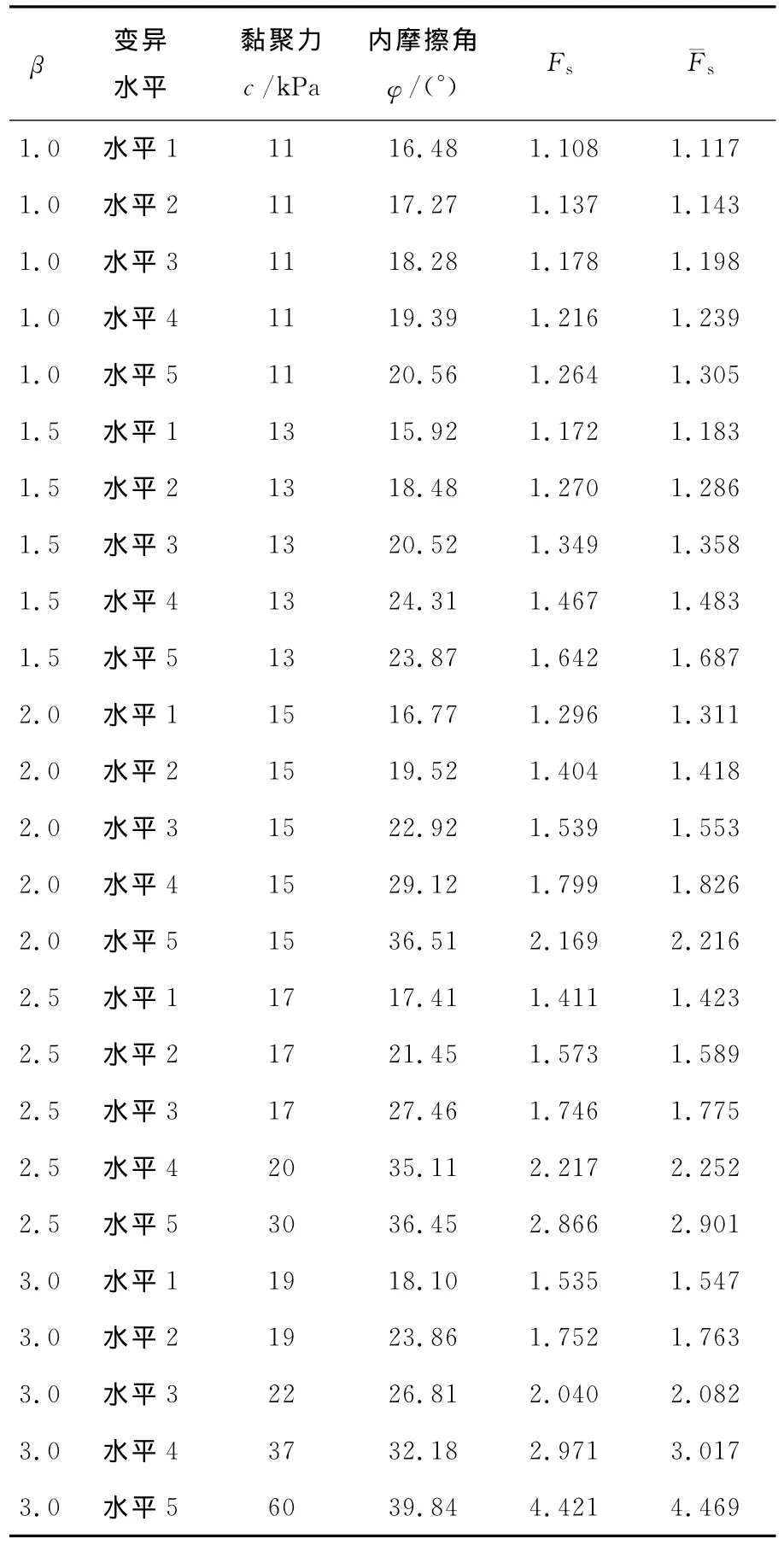
表5 不同條件下安全系數計算結果Table 5 Results of safety coefficient under different conditions

表5結果表明，在同一邊坡可靠指標β和參數變異水平下，均值安全系數Fs略小于安全系數均值ˉFs，但差異并不明顯，差值在0.05內［21］。根據表5結果作出不同變異水平下均值安全系數Fs隨邊坡可靠指標β的變化曲線，如圖3所示。

計算表明，不同土體抗剪強度指標變異水平條件下，均值安全系數Fs隨邊坡可靠指標β的提高而增大。總體而言，Fs隨β的增加呈現出逐漸增長的趨勢，增長速度在不同變異水平時有所差別。當抗剪強度指標變異性較小時（變異水平在水平3或以下水平），隨著β的增大，Fs的增長趨勢較為平緩，變化范圍為1.108～2.040；當抗剪強度指標的變異水平處于水平4或水平5時，曲線斜率逐漸加大，β的增加引起Fs的明顯增大，Fs變化范圍為1.216～4.421。

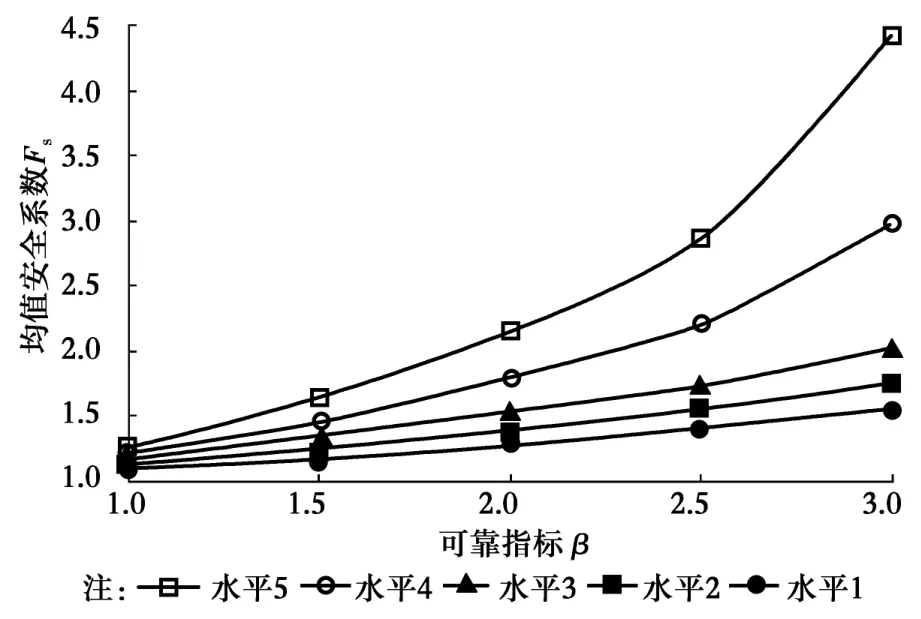
圖3 均值安全系數與邊坡可靠指標關系曲線Fig.3 Curve of relationship between mean safety factor and slope reliability index

另一方面，在同一β條件下，Fs的取值隨著土體抗剪強度指標變異水平的提高而呈現類似的增長規律，如圖4所示。當β＝1～2時，均值安全系數隨著變異水平的提高增長趨勢較為平緩；當β＝2～3時，隨著變異水平的提高，Fs的增長幅度加大，取值變化明顯。

圖4 均值安全系數與變異水平關系曲線Fig.4 Curve of relationship between mean safety factor and variation levels

為定量分析不同土體抗剪強度指標變異水平下可靠指標β與均值安全系數Fs的對應關系，運用冪函數對表5結果進行回歸分析［22］，建立可靠指標β與均值安全系數Fs的三參數函數關系式。

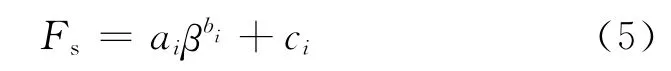
式中：β的取值范圍為β＝1.0～3.0，i＝1、2、3、4、5分別表示土體抗剪強度指標的5種變異水平，對應回歸參數如表6所列。

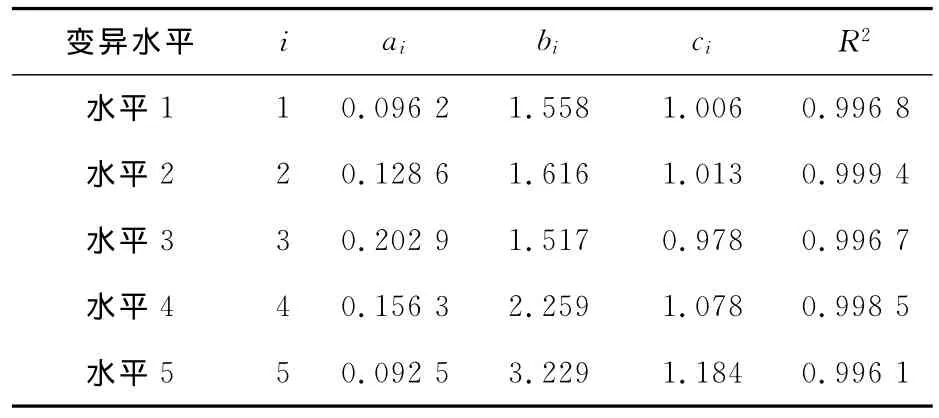
表6 不同變異水平下的回歸參數Table 6 Regression parameters under different levels of variation

表6中擬合優度R2取值均大于0.99，表明可靠指標β與均值安全系數Fs具有良好的冪函數回歸關系，兩者可進行有效換算。回歸參數中ai、ci的差異并不明顯，bi的取值恰好反映出Fs隨β的變化規律（i＝1、2、3時，bi取值在1.5左右，曲線增長較平緩；i＝4、5時，bi＞2.2，曲線增長較快），對應的回歸關系式可為不同變異水平下容許安全系數的選取提供參考。

中國工程地勘資料統計表明，土體抗剪強度指標普遍處于中等變異水平（對應于表2中水平3），個別情況甚至達到大變異水平（對應于表2中水平5），因而，有必要對傳統經驗性安全系數的取值進行優化。參照表5的計算結果及所建立的冪函數表達式，提出邊坡安全系數的取值應與可靠指標和土體抗剪強度指標變異水平相適應的技術原則，即以可靠性方法進行邊坡穩定性設計時，在選定分析模型和安全系數驗算方法條件下，應以可靠指標為基礎，同時考慮土體抗剪強度指標實際具有的變異水平合理選取穩定安全系數。

對于目前工程常用的設計安全系數Fs＝1.25的條件，根據文中計算結果可知，在土體抗剪強度指標的變異水平處于水平1情況下邊坡可靠指標β＝1.817；處于水平3時，對應的β＝1.213；處于水平5時β＝0.901，已不能滿足邊坡穩定性基本要求。若要求可靠指標β＝2.0，對應于抗剪強度指標變異水平處于水平3條件下的安全系數需提高至Fs＝1.539；當變異水平處于水平5時，則對應的安全系數將達到Fs＝2.169。

3 結 論

針對均質路堤邊坡穩定分析模型，基于Monte－Carlo法討論了土體抗剪強度指標變異性與邊坡失效概率的關系，分析了抗剪強度指標處于不同變異水平時均值安全系數Fs隨邊坡可靠指標β的變化規律，得到如下結論：

1）土體抗剪強度指標的變異性對路堤邊坡失效概率影響顯著。設計安全系數Fs＝1.25在抗剪強度指標變異性較小時（相當于文中水平3及以下水平）較為合理，在變異性較大時，如文中變異水平抽樣水平5時，β＝0.901，不可接受；對于通過常規地質勘查獲取的抗剪強度指標變異水平多處于水平3（中等變異水平）的情況，即便只達到目標可靠指標β＝2.0，對應的Fs取值亦需提高至1.539以上。

2）提出了基于可靠指標和土體抗剪強度指標變異水平的安全系數取值原則，建立了土體抗剪強度指標在不同變異水平下，邊坡可靠指標β與均值安全系數Fs的三參數冪函數表達式。

［1］祝玉學.邊坡可靠性分析［M］.北京：冶金工業出版社，1993.

［2］姚耀武，陳東偉.土坡穩定可靠度分析［J］.巖土工程學報，1994，16（2）：80－87.Yao Y W，Chen D W.Study on stability analysis of soil slopes［J］.Chinese Journal of Rock Mechanics and Engineering，1994，16（2）：80－87.（in Chinese）

［3］Wu T H，Kraft L M.Safety analysis of slopes［J］.Journal of the Soil Mechanics and Foundations Division，1970，96（2）：609－630.

［4］冷伍明，趙善銳.土工參數不確定性的計算分析［J］.巖土工程學報，1995，17（2）：68－74.Leng W M，Zhao S R.Analysis on the Uncertainties of Soil Properties［J］.Chinese Journal of Geotechnical Engineering，1995，17（2）：68－74.（in Chinese）

［5］張衛民.土體力學參數對土坡穩定安全系數影響分析［D］.杭州：浙江大學，2006.Zhang W M.Influence of soil parameters on soil slope safety factor of stability ［D］.Hangzhou：Zhejiang University，2006.（in Chinese）

［6］張繼周，繆林昌，劉峰.巖土參數的不確定性及其統計方法［J］.巖土力學，2008，28（6）：669－673.Zhang J Z，Miao L C，Liu F.Uncertainties of soil properties and its statistical method［J］.Rock and Soil Mechanics，2008，28（6）：669－673.（in Chinese）

［7］張繼周，繆林昌，王華敬.土性參數不確定性描述方法的探討［J］.巖土工程學報，2009，31（12）：1936－1940.Zhang J Z，Miao L C，Wang H J.Methods for characterizing variability of soil parameters ［J］.Chinese Journal of Geotechnical Engineering，2009，31（12）：1936－1940.（in Chinese）

［8］羅文強，王亮清，龔鈺.正態分布下邊坡穩定性二元指標體系研究［J］.巖石力學與工程學報，2005，24（13）：2288－2292.Luo W Q，Wang L Q，Gong J.Study on slope stability by dual index system based on normal distribution［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（13）：2288－2292.（in Chinese）

［9］黃景華，陳朝暉，莫玻，等.參數特性及分布形式對邊坡穩定可靠性影響的分析［J］.四川大學學報：工程科學版，2014，46（3）：23－30.Huang J H，Chen Z H，Mo B，et al.Influence analysis of characteristics and distribution types of soil parameters on slope reliability［J］.Journal of Sichuan University：Engineering Science Edition，2014，46（3）：23－30.（in Chinese））

［10］盛驟，謝式千，潘承毅.概率論與數理統計［M］.4版.北京：高等教育出版社，2008.

［11］高大釗.土力學可靠性原理［M］.北京：中國建筑工業出版社，1989.

［12］Duncan J M.Factors of safety and reliability in geotechnical engineering ［J］.Journal of Geotechnical and Geoenvironmental Engineering，2000，126（4）：307－316.

［13］李小勇.土工參數空間概率特征［M］.北京：原子能出版社，2006.

［14］包承綱.談巖土工程概率分析法中的若干基本問題［J］.巖土工程學報，1989，11（4）：94－98.Bao C G.Reliability method in geotechnical engineering［J］.Chinese Journal of Geotechnical Engineering，1989，11（4）：94－98.（in Chinese）

［15］吳興正.路基邊坡穩定可靠度計算中的不確定性問題研究［D］.成都：西南交通大學，2015.Wu X Z.Study on the uncertainty of stability reliability of subgrade slop［D］.Chengdu：Southwest Jiaotong University，2015.（in Chinese）

［16］傅旭東，趙善銳.用蒙特卡洛（Monte－Carlo）方法計算巖土工程的可靠度指標［J］.西南交通大學學報，1996，31（2）：164－169.Fu X D， Zhao S R. Appling the Monte－Carlo simulation to calculate the geotechnical reliability index［J］.Journal of Southwest Jiaotong University，1996，31（2）：164－169.（in Chinese）

［17］GEO－SLOPE International Ltd.邊坡穩定性分析軟件SLOPE／W用戶指南［M］.北京：冶金工業出版社，2011：30－32.

［18］中華人民共和國鐵道部.TB 10001—2005鐵路路基設計規范［S］.北京：中國鐵道出版社，2005.

［19］陳仲頤，周景星，王洪瑾.土力學［M］.北京：清華大學出版社，1994.

［20］中華人民共和國鐵道部.TB 10106—2010鐵路工程地基處理技術規程［S］.北京：中國鐵道出版社，2010.

［21］呂楊.土質路堤邊坡穩定可靠度分析方法探討［D］.成都：西南交通大學，2014.Lyu Y.Discussion on the method of stability reliability of embankment slope ［D］. Chengdu： Southwest Jiaotong University，2014.（in Chinese）

［22］李柏年，吳禮斌.MATLAB數據分析方法［M］.北京：機械工業出版社，2012.