一種新的簡化粒子群優化算法*
李曉靜
(廣西幼兒師范高等專科學校,廣西 南寧 530022)
一種新的簡化粒子群優化算法*
李曉靜
(廣西幼兒師范高等專科學校,廣西南寧530022)
針對粒子群算法在尋優中存在早熟和收斂精度不高等問題,論文對粒子位置的更新策略以及更新公式進行改進,提出了一種新的簡化粒子群優化算法(New Simple Particle Swarm Optimization,NSPSO),并將其在15個多極值基準函數進行全局最優化測試,實驗結果表明,NSPSO算法收斂的精度大大提高了,而且算法收斂速度也很快,對于高、低維復雜函數的優化均適用.
粒子群優化算法;簡化公式;群體智能;全局最優
0 引言
1995年,Kennedy和Eberhart發表研究論文首次提出了粒子群優化算法[1](particle swarm optimization,PSO),該算法是通過觀察鳥群集體出動捕食的相互協助行為而提出的一種仿生優化算法,該算法收斂速度和全局優化能力均表現良好.而且該算法與遺傳算法相比,算法的參數更少,使用也更簡單,因此算法自提出后已被廣泛用于各種工程實踐的優化問題.然而,這種隨機算法本身的尋優過程均是利用迭代機制進行更新,算法往往快速收斂到一定程度之后就停滯了,即所謂“早熟”.因此算法對復雜問題的收斂精度不高.針對這個問題,很多學者對粒子群算法提出了許多改進的方案,如基于逃離局部最優的DPSO[2],去掉了飛行速度項的一種簡化粒子群算法[3],通過釋放因子增強可利用的種群信息的改進算法[4],綜合學習的粒子群算法[5](CLPSO),以及其他的改進算法[6-8].這些改進算法都在一定程度提高了算法的收斂精度,但都還沒有挖掘出粒子群算法最大潛力.
群智算法或者仿生算法都存在“早熟”現象,既能抑制算法過早出現“早熟”而又能保證算法的收斂是每種群智算法的改進目標,要達成這個目標就必須在算法收斂的同時,盡可能的保持算法種群的多樣性.為此,筆者提出一種新的簡化粒子群算法,即NSPSO算法.算法對粒子群算法的更新策略和更新公式進行一些改進,使改進后粒子群算法在迭代優化過程時,一定程度上保持了種群的多樣性,同時算法還具有拋棄某些粒子收斂停滯位置尋找新位置的能力.
1 粒子群優化算法
由于PSO優化算法是從鳥群捕食行為的基礎上提出的,因此在算法中的一個粒子相當于鳥群中的一只鳥.而每一只鳥出去捕食均可能找到食物,故每一個粒子(鳥)可以視為待優化問題的一個可能解(食物),算法尋優的過程就相當于鳥群尋找食物的過程.該算法搜尋的過程需要通過每個個體的個體極值與種群極值之間的信息分享來改變搜索的路徑,算法中粒子的更新公式如下:
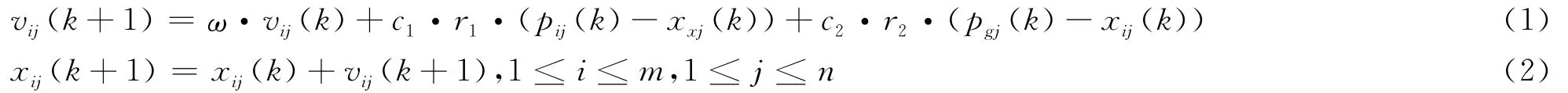
其中,m為種群數;n為解空間的維數;Xi=(χi1,…,χin)為第i個粒子的目前位置;Vi=(vi1,vi2,…,vin)表示第i個粒子的飛行速度;Pi=(pi1,pi2,…,pin)為到目前為止粒子i搜索到的最好位置,稱為個體極值;Pg=(pg1,pg2,…,pgn)為到目前為止,整個找到的最好位置,稱為種群極值.j為粒子位置(共n維)的第j維;k表示進化(搜索)的代數(輪數),c1和c2為記憶因子,r1和r2為兩個0~1之間產生的隨機數.
事實上,通過文獻[9]證明:將粒子速度vid約束在[-vmax,vmax]等價于添加約束因子α的基礎上,文獻[3]通過嚴格數學推導,證明粒子群算法的速度參數對于算法進化是無關的.如若將速度這一參數直接去掉,整個算法收斂的精度與速度會受到影響.因此,算法中的更新公式可以簡化為[2]:
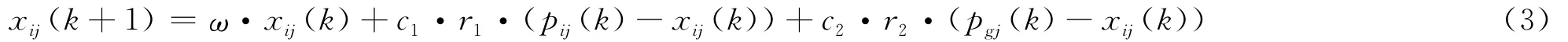
(3)式右邊的第1項表示過去搜索結果對現在的影響,ω為慣性系數;第2項則表示粒子的自身調節進化;第3項表示粒子間的信息交流.
2 粒子群優化算法的改進
2.1減少每個粒子的更新位置
從更新式(1)和式(2)均可知,在以往的粒子群算法中,每個粒子均以更新公式進行單點位置的更新.每一輪的尋優中,算法總是將粒子的位置一次性更新,使粒子個體大幅度向個體和種群的極值靠攏,如果尋優的問題不太復雜,一般的PSO算法均可以快速的找到最優解.但是,如果待解決的問題相對來說更加復雜,且具有多個極值點的時候,算法就極可能快速的陷入某個局部最優解而無法跳出來,最后種群中的個體都“聚集”在某一個點周圍,即算法出現“早熟”現象.為此,筆者借鑒蜂群算法中更新策略,提出將PSO算法在每一輪中,僅利用隨機的辦法生成T(T取1~5)個位置,對每個粒子的T個位置進行更新.這樣,粒子在迭代更新過程中可以比較某個位置的更新是否比不更新前的位置更具有優勢,優化的過程更加具有針對性,粒子的位置也是部分的、慢慢的向最優個體靠攏.
2.2保持種群的多樣性
將更新公式(3)改為:
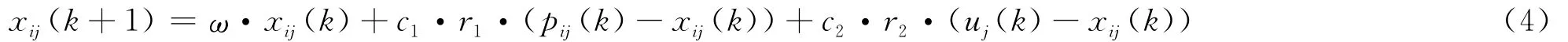
對于式中u的數學描述如下:

其中,η=1-0.9*(max_iter-iter)/max_iter為0.1~1線性遞增;pneighbour個體neighbour的極值,且i≠neighbour;這樣可以在種群搜索的初始階段,算法注重種群搜索的速度,而到了搜索的后半程,算法則更注重種群的多樣性,避免“早熟”.
2.3添加控制參數“limit”
用于記錄某個粒子被更新的次數,若某個粒子連續經過limit次迭代更新之后,其個體極值依然沒有得到改善,表明該粒子(解)已經陷入局部最優,那么就要放棄這個解,并重新隨機生成一個新解來代替χi,這樣使粒子在迭代進化過程中完成“自救”,并能增加種群的多樣性.其中
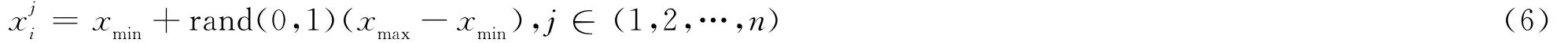
改進算法的具體實現步驟如下:
1)給定算法的參數:種群規模m;記憶因子c1,c2;影響參數ω以及最大迭代次數Gmax.
2)在待解決問題的搜索范圍內隨機生成m個粒子的初始位置(每個粒子有n維);
3)根據適應度函數公式,計算每個粒子的適應值;
4)以當前每個粒子的位置作為該粒子經歷的最好位置P,并求出整個種群的最優位置Pg;
5)對于種群的所有粒子(for i=1to m);
6)對于粒子i,在1到n個位置間隨機生成T個位置,并按公式(5)對該粒子的T個位置進行更新,并記sol為粒子i更新前的位置,sne為粒子i更新后的位置;
7)對于粒子i,計算其適應值,并與更新前的適應值進行比較,若它的適應值更好,就以更新后的位置sne作為粒子i這一輪迭代的位置,同時粒子i的控制參數“limit”歸0;否則,以更新前的位置sol作為粒子i這一輪迭代的位置,同時粒子i的控制參數“limit”加1;
8)對于粒子i,將其適應值與它經歷過的最好位置P的適應值進行比較,若較好,則將其更新位置P;
9)對于粒子i,比較其適應值和種群中的最好位置Pg的適應值,如果它的適應值更好,更新Pg;
10)每完成一輪迭代,判斷是否有粒子的控制參數“limit”達到上限,若存在,則根據(6)式生成一個新的解代替它,并將其對應的控制參數歸0;
11)判斷是否滿足停止條件,若滿足,則輸出最優值,否則轉到5).
3 仿真實驗及結果分析
為了驗證筆者提出的改進粒子群算法的性能,選取了多個經典測試函數對新算法進行測試,其表達式如下,并將之與幾種有名的改進算法:CLPSO、IPSO[5]、HPSO[6]的結果進行比較.所用的測試函數及其搜索范圍、最優點、初始化范圍等信息見表1:

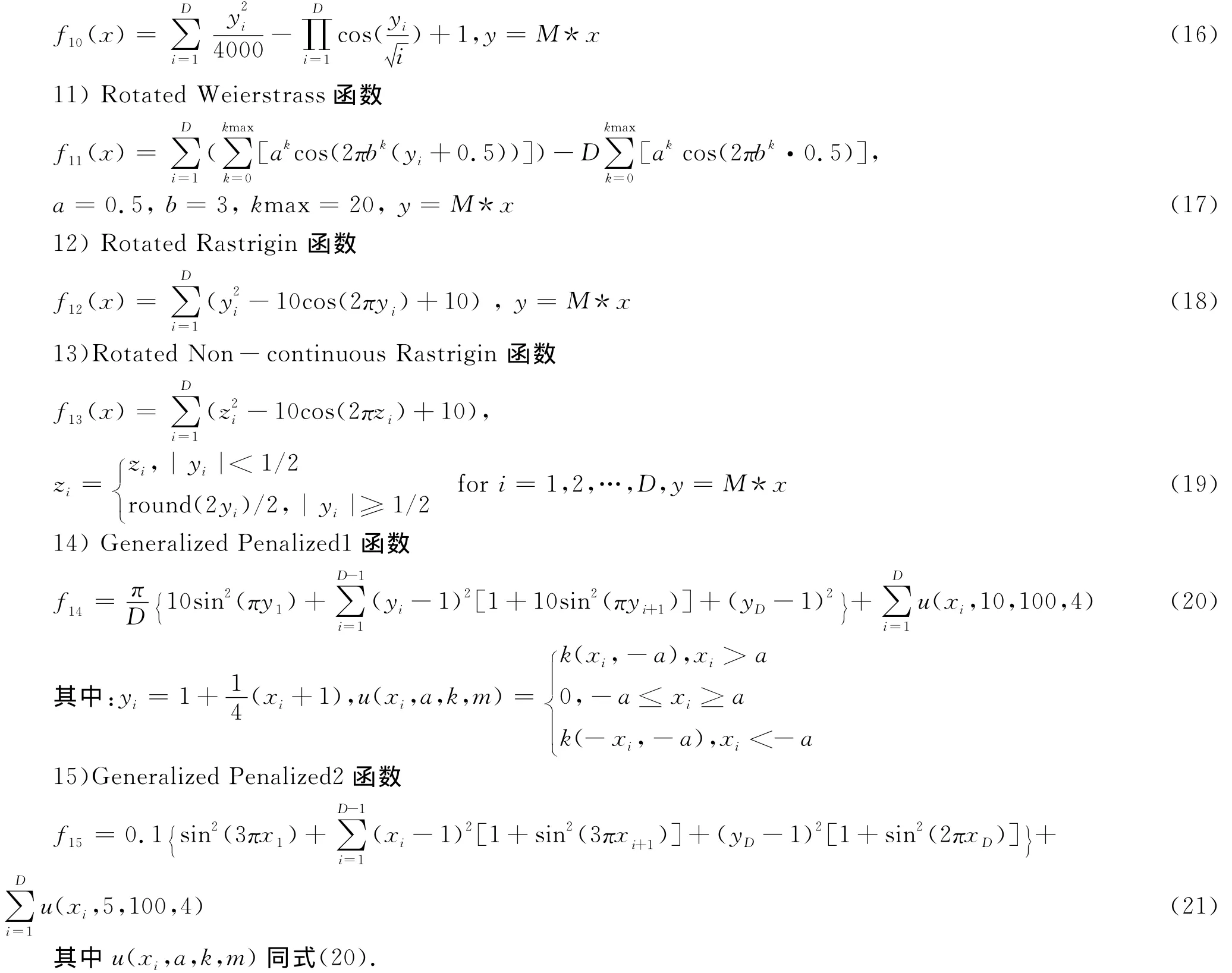

表1 測試函數的全局最優點、搜索范圍以及初始化范圍Tab.1 Test global optimum function,search range and initializing range
在改進算法中,實驗計算需要確定的參數c1=c2=2;種群規模m=50;最大迭代次數3500次;每個函數獨立運行20次;測試函數的維數是30維.對于CLPSO、IPSO、HPSO等算法均采用各自文獻中的默認參數,其中他們的最大迭代次數分別是5000次,4000次和200000次.其比較結果見表2:
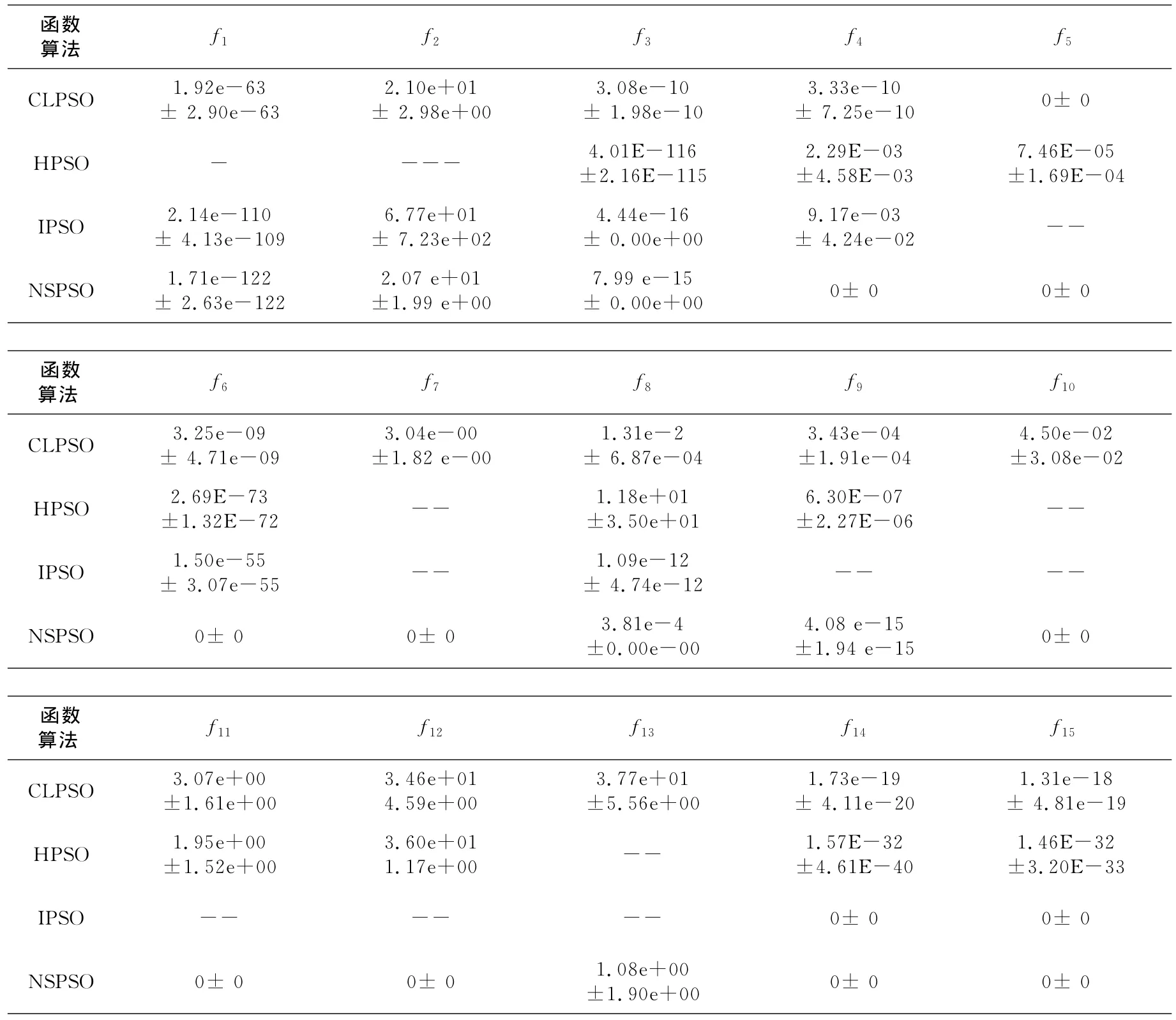
表2 函數為30維的測試結果Tab.2 30-dimensional function test results
從表2可以看出,筆者提出的NSPSO算法對絕大部分函數的收斂精度遠高于CLPSO、HPSO和IPSO算法,而且在15個測試函數中,筆者提出的NSPSO算法有9個函數搜索到理論優解,還有一個函數(Sphere函數)其精度也幾乎達到了理論值,從而證明該算法穩定性和有效性.而HPSO算法只有在第3個測試函數Ackley上測試精度最好,但其耗費的迭代次數太大.
進一步地,為了觀察該算法在迭代過程中適應度值的變化情況,將NSPSO算法和CLPSO在300維的Rastrigin函數、Ackley函數、Weierstrass函數以及Griewank函數上收斂過程進行對比.見圖1~4.
從圖1~4的收斂曲線對比可以看出,對更高維的測試函數進行全局尋優時,NSPSO算法的收斂曲線在搜索開始后就迅速下降,隨著搜索的進一步深入,筆者提出的NSPSO算法與CLPSO算法的收斂曲線的距離也越來越大(即兩種算法收斂精度差距越來越大:NSPSO算法收斂速度明顯快于CLPSO算法).進一步地,從圖中我們還可以看出,NSPSO算法的曲線是一直平滑的,而CLPSO的收斂曲線則在搜索的初始階段和搜索的中期均出現一定的不規則階梯型,即搜索出現停滯現象,這說明該算法在搜索過程中在不停的陷入局部最優解,為此,算法不得不花費一定的搜索時間逃出局部最優解,因此該算法的收斂速度和收斂精度均遜于提出的NSPSO算法.
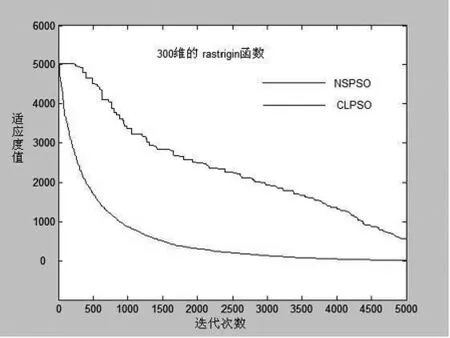
圖1 NSPSO和CLPSO對300維Rastrigin函數的收斂曲線對比圖Fig.1 NSPSO and CLPSO convergence curve 300 Victoria Rastrigin function comparison chart
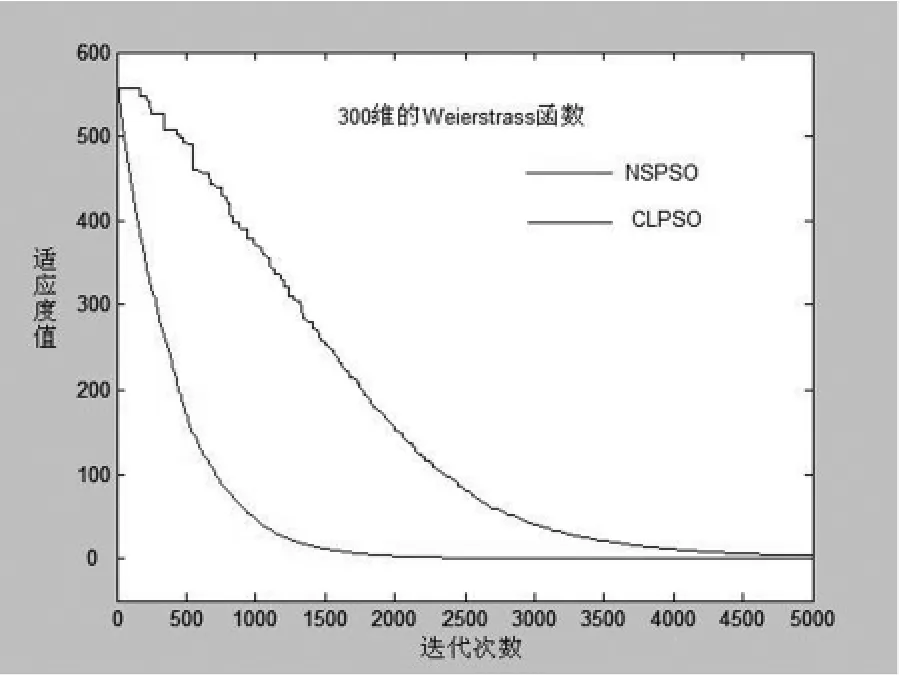
圖2 NSPSO和CLPSO對300維Ackley函數的收斂曲線對Fig.2 NSPSO and CLPSO convergence curve dimensional Ackley function 300Comparison Chart
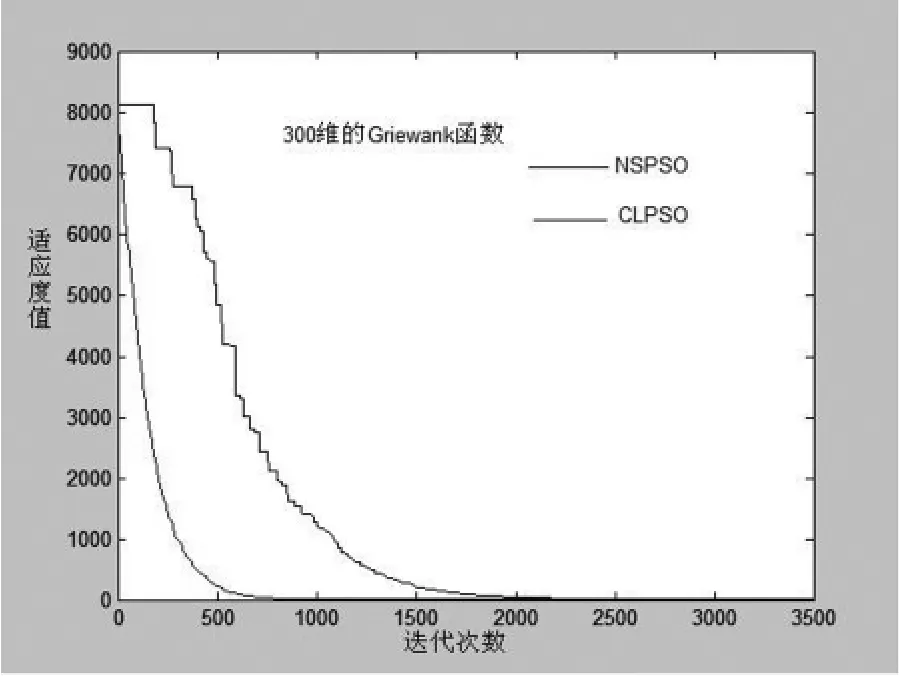
圖3 NSPSO和CLPSO對300維Griewank函數的收斂曲線對比圖Fig.3 NSPSO and CLPSO convergence curve 300 Victoria Griewank function comparison chart
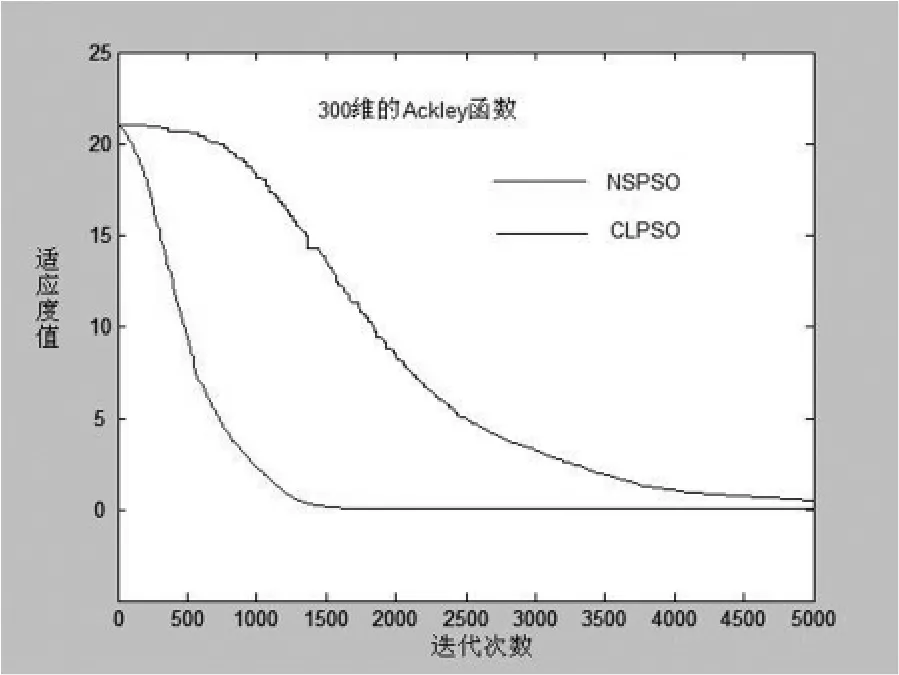
圖4 NSPSO和CLPSO對300維Weierstrass函數的收斂曲線對比圖Fig.4 NSPSO and CLPSO convergence curve 300 Victoria Weierstrass function comparison chart
4 結論
筆者提出了一種簡化的粒子群改進算法(NSPSO算法),該算法不僅去掉了標準PSO算法中的粒子飛行速度項V部分,而且也拋棄了標準PSO算法中的向個體極值靠攏和向種群極值靠攏的部分,取而代之的是論文提出的粒子更新方法:粒子以一定概率選擇向其他粒子或種群極值進行部分維數鄰域搜索新的位置,若搜索到的位置更好則更新粒子的位置,否則粒子的位置不更新.同時,論文還添加一個控制參數用以判斷是否放棄粒子目前的位置而重新生成新的位置.實驗結果表明,改進算法的全局尋優能力與其他改進算法相比具有較大優勢,而且筆者的改進算法NSPSO收斂速度也快、精度也高,對于高、低維的復雜函數優化問題均可行.
[1]Kennedy J,Eberhart R.Particle Swarm optimization[C].In:IEEE Int 1Conf on Neural Networks.Perth,Austraial,1995:1942-1948.
[2]Omranpour H.,Ebadzadeh M.,Shiry S.et al.,Dynamic Particle Swarm Optimization for Multimodal Function[J].Artificial Intelligence,2012,1(1):1-10.
[3]胡旺,李志蜀.一種更簡化而高效的粒子群優化算法[J].軟件學報,2006,18(4):861-868.
[4]任小波,楊忠秀.粒子群優化算法的改進[J].計算機工程.2010,36(7):205-207.
[5]Liang J J,Qin A K,Suganthan P N,et al.Comprehensive learning particle swarm optimizer for global optimization of multimodal functions [C].IEEE Transactions on Evolutionary Computation,2006,10(3):281-295.
[6]紀震,周家銳,廖惠連,等.智能單粒子優化算法[J].計算機學報,2010,33(3):556-561.
[7]Chen Chia-Chong.Hierarchical Particle Swarm Optimization for Optimization Problems[J].Tamkang Journal of Science and Engineering,2009,12(3):289-298.
[8]劉愛軍,楊育,李斐,等.混沌模擬退火粒子群優化算法研究及應用[J].浙江大學學報:工學版,2013,47(10):1722-1730.
[9]Clerc M.The swarm and the queen:Towards a deterministic and adaptive particle swarm optimization[C].Proc.The Congress on Evolutionary Computation.Washington,1999:1951-1957.
[責任編輯 蘇 琴][責任校對 黃招揚]
A New Simplified Particle Swarm Optimization
LI Xiao-jing
(Guangχi College for Preschool Education,Nanning530022,China)
Concerning the problems of premature and low convergence accuracy for the particle?swarm?algorithm in search of optimization,update strategy and formula of the particle position have been made improvements in this paper,and a new simple particle swarm optimization(NSPSO)is proposed. Through global optimization tests in 15multiple maximum benchmark functions,the experimental results show the convergence accuracy of NSPSO has improved greatly and the rate of convergence become faster,which can be applied in the optimization for high and low dimensional complicated functions.
particle swarm optimization;Simplified formula;swarm intelligence;global optimality
TP18
A
1673-8462(2015)01-0083-07
2014-09-10.
廣西青年基金項目(2013GXNSFBA019227);國家自然科學基金項目(41065002).
李曉靜(1982-),女,河南許昌人,碩士,廣西幼兒師范高等專科學校講師,研究方向:數據挖掘、應用數學.

