一種全工況適應的全輪獨立驅動車輛車速估計方法

陽貴兵，李長兵，廖自力，馬曉軍，劉春光

（裝甲兵工程學院陸戰平臺全電化技術重點實驗室，北京100072）

一種全工況適應的全輪獨立驅動車輛車速估計方法

陽貴兵，李長兵，廖自力，馬曉軍，劉春光

（裝甲兵工程學院陸戰平臺全電化技術重點實驗室，北京100072）

為解決全輪獨立驅動車輛車速估計難的問題，提出了一種全工況適應的車速估計方法。該方法以參數自適應卡爾曼濾波算法為基礎，采用左右側分離估計，并設計模糊控制器對濾波系數進行自適應調節，通過判斷車輛的行駛工況和路面條件，設計自適應切換條件，當車輪滑轉/滑移狀態超過預設值，切換為縱向加速度積分估計。利用硬件在環實時仿真實驗對所提出的車速估計方法的有效性和準確性進行了驗證，仿真結果表明，該方法在多工況運行下具有很好的估計精度，具有普遍應用價值。

控制科學與技術；車速估計；卡爾曼濾波；全工況適應；全輪驅動

0 引言

縱向車速是車輛非常重要的狀態參數之一，其估計的精度直接決定了車輛驅動防滑控制（ASR）、制動防抱死系統（ABS）以及直接橫擺力矩控制（DYC）等一系列車輛穩定性控制的控制效果［1］。

全輪獨立驅動車輛的縱向車速的獲取，目前主要有兩種方法：一是借助光學傳感器或者GPS高精度測速儀［2］；二是基于普通車載傳感器的估計方法［3］。第一種方法，由于涉及的成本過高，不適于量產及一般性的研究，因此第二種方法成為目前研究的主流。估計方法中，最簡單的是車身加速度直接積分法，但由于積分過程中，系統噪聲產生的誤差不斷累計，長時間積分，會導致估計結果發散，并不適應于長時間的車速估計［4］。一些學者采用了非線性車輛模型和輪胎模型，運用非線性估計算法對縱向車速進行估計［5-6］，這類方法要求的車輛和輪胎參數較多，且嚴重依賴參數的精確度，因此，在實際運用中受到很大的限制。除此外，文獻［7］提出了一種基于卡爾曼濾波和ABS控制輸入的車速估計方法，但是該方法使用的前提是有ABS介入，當車輪處于大滑轉或者抱死情況下，該方法無法獲得準確的估計結果。基于此，文獻［1］提出了一種多方法融合的車速估計方法，但由于沒有考慮多電機運行工況，因此只適合在穩態小轉向、直線加速/制動工況下的車速估計。

由于全輪獨立驅動車輛可完成諸如小半徑滑移轉向、原地中心轉向等特殊轉向方式，因此，其縱向車速估計方法，必須要有全工況適應性。本文以某型8輪獨立驅動車輛為研究對象，在文獻［1］的基礎上，對卡爾曼濾波估計的輪速進行優化選取，并采用左右側分離估計再求加權平均的方法，濾波過程中的過程噪聲和量測噪聲采用模糊控制器進行自適應調節，通過判斷行駛工況和路面條件對自適應切換進行設計，當車輪滑轉/滑移狀況超過預設閥值，切換為基于車身3軸加速度傳感器信號的積分估計。最后，通過多種行駛工況的硬件在環實時仿真實驗，驗證本文所提出的車速估計方法全工況運行下的有效性和準確性。

1 車速估計器結構及原理

圖1 車速估計器結構圖Fig.1 The structure of vehicle speed estimator

車速卡爾曼濾波估計（見圖2），采用左右側分離估計再進行加權平均的方法，這種方法能有效滿足車輛在小半徑轉向、原地中心轉向時，兩側輪速不同甚至一側為正、一側為負的情況下，對車速進行準確估計。

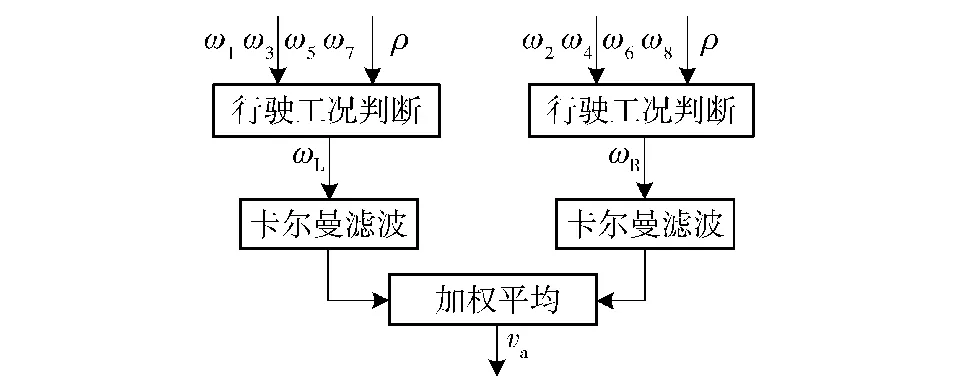
圖2 車速卡爾曼濾波估計Fig.2 Kalman filter estimation

ω1、ω3、ω5、ω7表示左側4個車輪的轉速；ω2、ω4、ω6、ω8表示右側4個車輪的轉速；駕駛信號為驅動踏板信號和制動踏板信號，以左側估計算法為例，首先根據駕駛信號判斷車輛處于驅動還是制動工況，按照驅動工況取最小值，制動工況取最大值的原則，選取ω1、ω3、ω5、ω7中的最優值作為卡爾曼濾波的基準輪速ωL.

由于本文研究車輛為全輪驅動車輛，因此，車輛在低附著路面急加速、緊急制動或者其他特殊工況運行時，會出現車輪滑轉或者抱死的情況，當所有車輪都發生比較大的打滑或者抱死，此時，基于輪速濾波的方法顯然無法準確估計出車速，因此，本文以車輪周向加速度am與車身縱向加速度aa的差值Δa為基礎，判斷車輪滑轉/滑移狀態，通過路面附著條件μ和駕駛信號ρ設計切換條件，當Δa的值超過預設閾值，則自動切換成基于aa積分的車速估計。

2 卡爾曼濾波器設計

2.1 車速卡爾曼濾波算法

離散卡爾曼濾波算法的過程方程和量測方程分別為

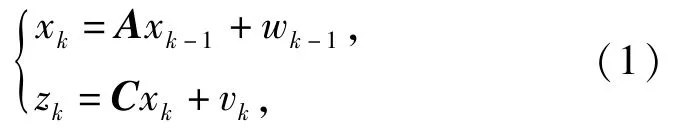
式中：k為采樣時刻；xk、zk分別為系統估計值和測量值；A、C分別為傳遞矩陣和量測矩陣；wk-1、vk分別為過程噪聲和量測噪聲。卡爾曼濾波過程可由下面5個式子進行描述：

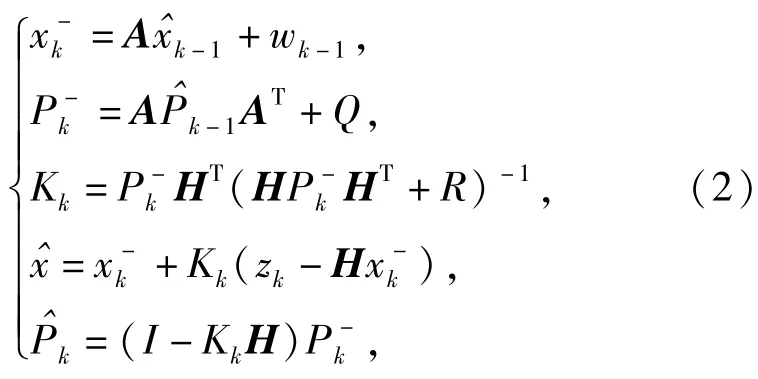
式中：P為誤差協方差矩陣；K為卡爾曼濾波增益；Q為過程噪聲wk的方差；R為量測噪聲vk的方差。

本文研究的車輛為具有雙前橋轉向8輪獨立驅動車輛，車輛單軌運動學模型如圖3所示。

圖3 車輛單軌2自由度運動學模型Fig.3 2 DOF single track kinematics model of vehicle

圖3中：vmi表示第i軸車輪周向速度的縱向分量；ωi為第i軸車輪的角速度；r為車輪半徑，δ1、δ2分別為1、2軸轉向角。

不考慮車輛高低向運動，依據線性2自由度車輛模型，車輛質心加速度與縱向車速的關系為

式中：γ為橫擺角速度。

車輪周向速度的縱向分量與縱向車速的關系為

式中：Δv為由于滑轉/滑移所造成的輪邊速度與縱向車速的差值。

（3）式和（4）式離散化得

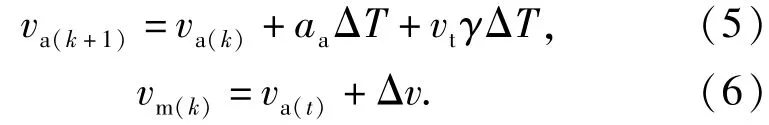
將（5）式中的vtγΔT定義為過程噪聲wk，將Δv定義為量測噪聲vk，得到卡爾曼濾波的過程方差和量測方程分別為（7）式和（8）式。

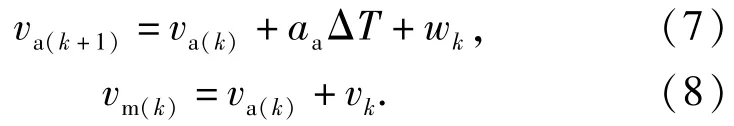
2.2 濾波器系數自適應調節

卡爾曼濾波算法的核心問題是對噪聲的描述和處理，假設過程噪聲wk和量測噪聲vk是均值為0的高斯白噪聲，其方差分別為Q和R.

由（5）式可知，過程噪聲wk=vtγΔT，γ可由車身橫擺角速度傳感器獲取，vt也可以用γ線性表示，ΔT為采樣周期，在實際系統中是一個常值。因此，wkΔT的方差Q可表示為γ的二次函數Q=κγ2，其中：κ值與橫向加速度at有關，at越大，κ值越大，at由加速度傳感器獲取。

而量測噪聲是由于車輪的滑轉/滑移運動所致，用Δa=|aa-am|來描述車輪的滑轉/滑移狀態。當Δa較小時，R也較小，反之，R值也較大。本文采用模糊規則對R值進行調節，模糊控制器的輸入為Δa以及Δa的變化率Δa′，輸出為R值。表1為模糊推理規則，分別以S、M、L、VL代表小、中、大和很大。圖4～圖6為模糊控制器輸入輸出的隸屬度函數，圖7為R映射曲面。

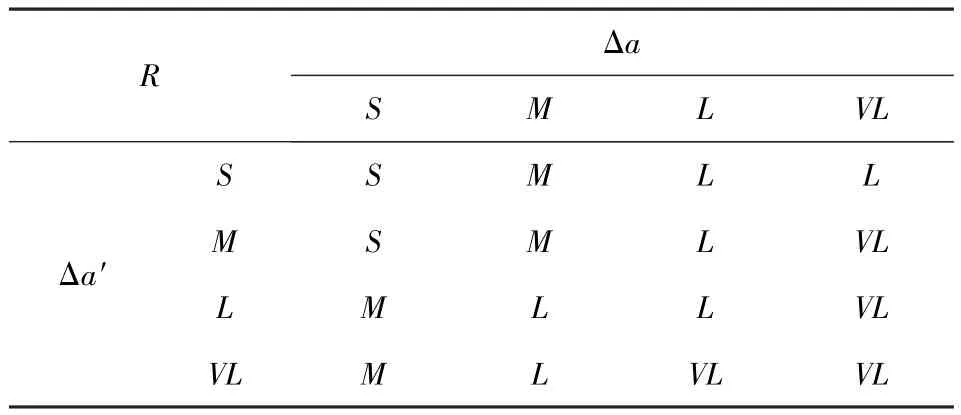
表1 R的模糊推理規則Tab.1 Fuzzy reasoning rule for R

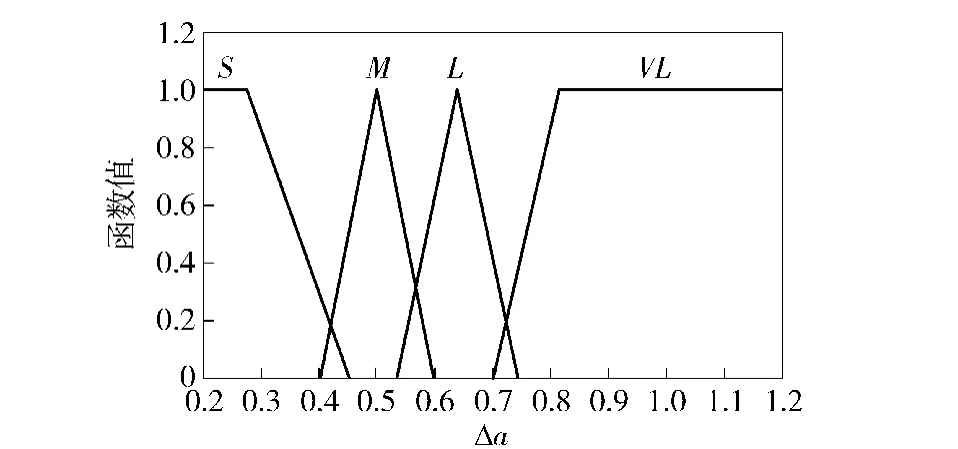
圖4 Δa的隸屬度函數Fig.4 Membership function of Δa

3 自適應切換設計

基于縱向加速度積分的車速估計，其算法為

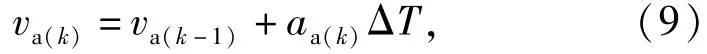
式中：va（k-1）為切換為積分估計前一個時刻卡爾曼濾波所估計的車速，以保證車速估計的連續性。

切換條件的設置，是本文研究的一個重點。本文選擇Δa值作為切換條件。經過前期一系列仿真發現，當采用固定某一個Δa值作為切換閾值時，在不同附著條件的路面、不同行駛工況下，估計的效果也不同。由于Δa只是表征車輛質心加速度與輪邊加速度的差，并不能表示二者速度的差，因此，會出現Δa很小而實際車速與車輪周向速度差別較大的情況。以圖8所示的低附著路面加速行駛時為例，在6 s之后，8個車輪中的最小輪速與車速的增加趨勢基本相同，二者的加速度值接近，Δa很小，但是速度差較大。如果在此情況下仍然以濾波方法估計車速，顯然會出現較大的誤差。

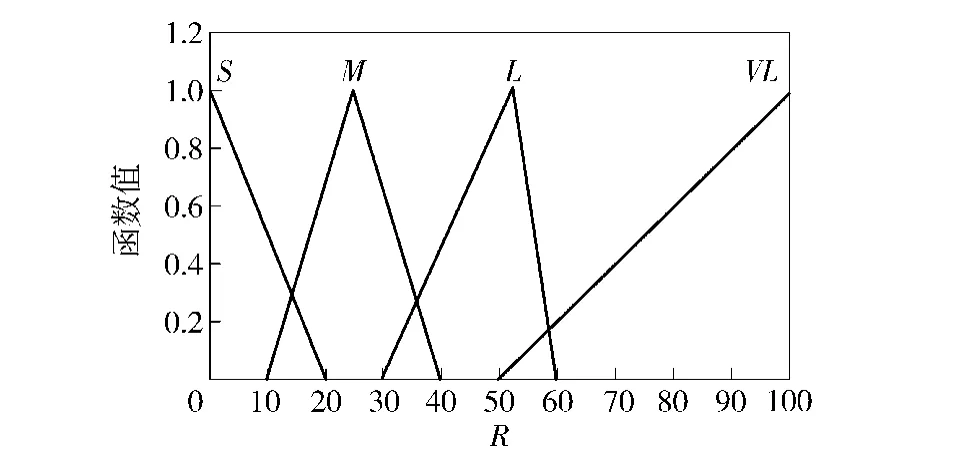
圖6 R的隸屬度函數Fig.6 Membership function of R

圖7 R的映射圖Fig.7 R mapping

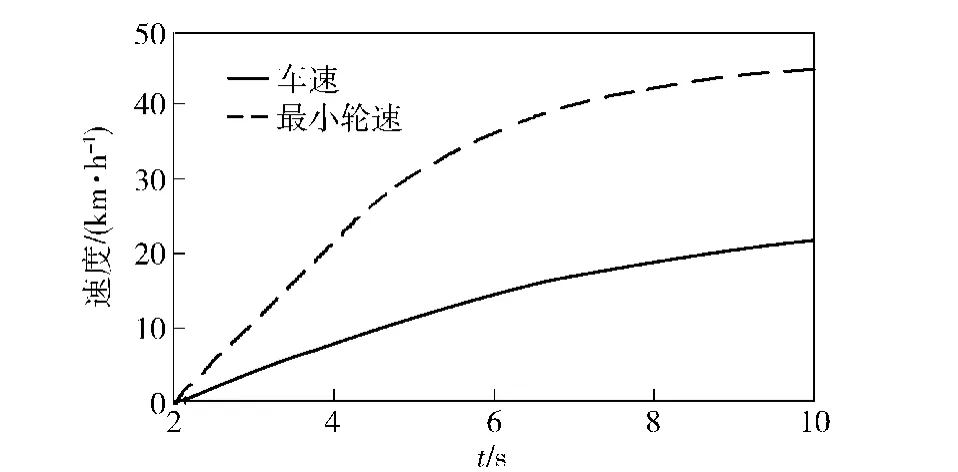
圖8 車輛低附著路面加速行駛速度曲線Fig.8 Curves of accelerated running on low adhesion road

為避免上述情況的出現，本文擬采用自適應切換的方法，針對不同路面附著條件，不同行駛工況，采用不同的Δa值作為切換閾值。行駛工況主要是判斷是否為急加速或緊急制動工況，可由加速/制動踏板開度ρ表示，ρ∈［-1，1］，當|ρ|＞0.8即為急加速或者緊急制動行駛。路面附著條件可由附著系數μ表示，分3種路面：高附著路面（μ＞0.8）、一般路面（0.4＜μ＜0.8）、低附著路面（μ＜0.4）.切換閾值Δa設置可由（10）式表示。

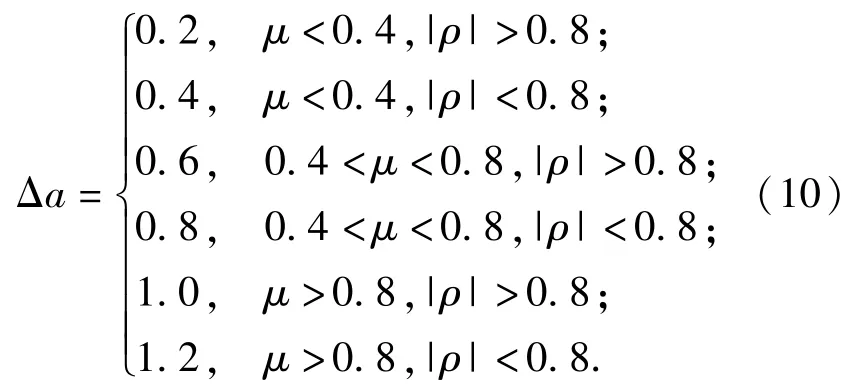
路面附著系數μ采用文獻［8］的方法進行估計。

4 實驗驗證及分析

由于樣車還未生產，本文采用基于實車中央控制器的硬件在環實時仿真實驗對所提出的車速估計算法進行驗證分析，硬件在環實時仿真實驗是樣車研制過程中必不可少的一環，可以減少樣車的調試周期、降低調試成本以及安全風險，本文硬件在環實時仿真平臺結構如圖9所示。

該平臺包括駕駛員操縱系統、控制系統、電機驅動系統以及動力學實時仿真系統4個部分，其中電機驅動系統與控制系統采用Flexray總線通信，其他系統采用CAN總線進行通信。將車速估計算法以代碼形式下載到實車中央控制器，進行實時仿真實驗。

為了能夠客觀全面驗證車速估計算法，本文設計了3種路面，7種不同的行駛工況。高附著路面行駛，設計了直線加速+大半徑轉向、低速小半徑轉向、原地中心轉向3種行駛工況。一般路面和低附著路面分別設計了急加速和緊急制動兩種行駛工況。高附著路面行駛工況，主要是驗證卡爾曼濾波算法估計的準確性。一般路面急加速和緊急制動工況主要是驗證兩種估計算法切換估計的準確性。低附著路面急加速和緊急制動工況主要是驗證積分估計算法的準確性。仿真條件設置如下：

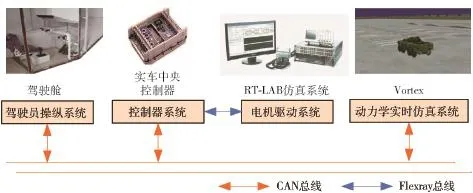
圖9 硬件在環實時仿真平臺Fig.9 Hardware-in-loop real-time simulation platform

1）高附著路面行駛工況。直線加速行駛+大半徑轉向，油門踏板ρ=0.8，4 s之后，方向盤打過120°轉角（滿程為900°）。低速小半徑轉向，油門踏板ρ=0.5，0.6 s后方向盤打過500°.原地中心轉向，油門踏板ρ=0.5，方向盤滿程。

2）一般路面行駛工況。μ=0.6.急加速行駛時，油門踏板ρ=1.0.緊急制動時，車輛從55 km/h處進行緊急制動，制動踏板ρ=-1.

3）低附著路面行駛工況。μ=0.2.急加速行駛時，油門踏板ρ=1.0.緊急制動時，從10 s開始，制動踏板ρ=-1.

仿真結果如圖10～圖12所示。仿真車速為Vortex軟件反饋的車速，可作為參考車速。

各種行駛工況下估計車速的最大誤差見表2.

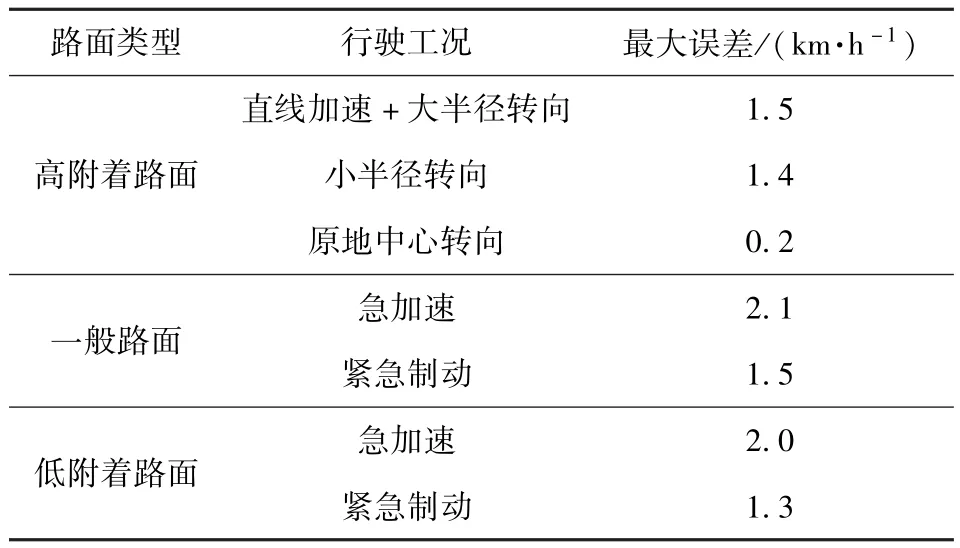
表2 車速估計最大誤差表Tab.2 Estimated maximum error of vehicle speed

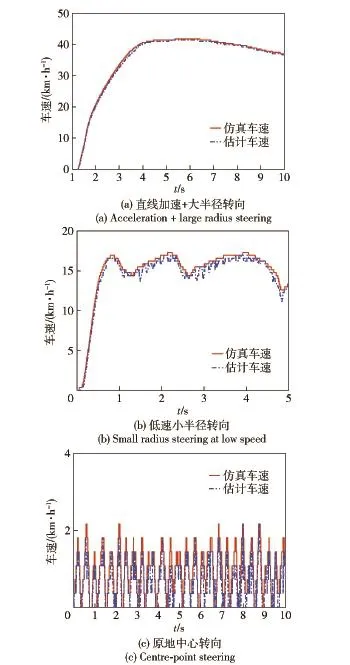
圖10 高附著路面行駛Fig.10 Driving on high adhesion road

由表2可知，在所有運行工況下，估計的車速與仿真車速誤差都比較小，估計精度較高，從而驗證了本文所提出的車速估計算法對全工況估計的準確性。

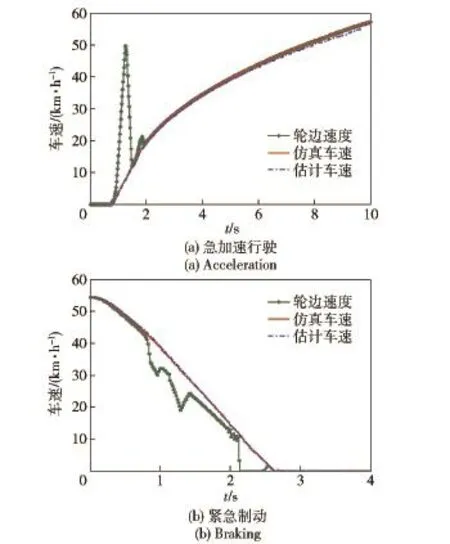
圖11 一般路面行駛Fig.11 Driving on middle adhesion road

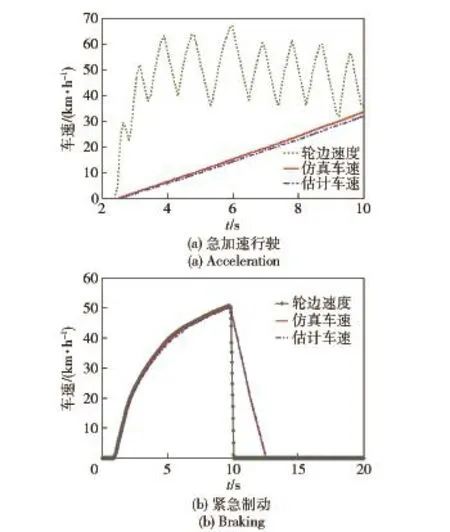
圖12 低附著路面行駛Fig.12 Driving on low adhesion road

5 結論

本文提出了一種基于輪速卡爾曼濾波與車身縱向加速度積分的車速估計方法。結合車輛運動學模型，建立了車速卡爾曼濾波估計的過程方程和量測方程，并采用模糊控制器，對濾波過程噪聲的方差和量測噪聲的方差進行自適應調節，設計了基于行駛工況與路面附著條件的自適應切換方法，當車輪滑轉/滑移狀態超過設定閥值時，切換為縱向加速度積分估計。

借助硬件在環仿真平臺，設計了多種行駛工況，對本文所提出的車速估計方法的有效性和準確性進行了驗證，從而為全輪獨立驅動車輛提供了一種全工況適應的縱向車速估計方法。

（

）

［1］ 褚文博，李深，江青云，等.基于多信息融合的全輪獨立電驅動車輛車速估計［J］.汽車工程，2011，33（11）：962-965. CHU Wen-bo，LI Shen，JIANG Qing-yun，et al.Speed estimation for all-wheel drive vehicles based on multi-information fusion［J］.Automotive Engineering，2011，33（11）：962-965.（in Chinese）

［2］ Nurhadiyatnal A，Hardjono B，Wibisono A，et al.Improved vehicle speed estimation using gaussian mixture model and hole filling algorithm［C］∥International Conference on Advanced Computer Science and Information Systems（ICACSIS）.Bali，Indonesia：IEEE，2013：451-456.

［3］ 陳慧，高博麟，徐帆.車輛質心側偏角估計綜述［J］.機械工程學報，2013，49（24）：76-94. CHEN Hui，GAO Bo-lin，XU Fan.Review on vehicle sideslip angle estimation［J］.Journal of Mechanical Engineering，2013，49（24）：76-94.（in Chinese）

［4］ 余卓平，高曉杰.車輛行駛過程中的狀態估計問題綜述［J］.機械工程學報，2009，45（5）：20-32. YU Zhuo-ping，GAO Xiao-jie.Review of vehiele state estimation problem under driving situation［J］.Journal of Mechanical Engineering，2009，45（5）：20-32.（in Chinese）

［5］ Shraim H，Ananou B，Fridman L，et al.Sliding mode observers for the estimation of vehicle parameters，forces and states of the center of gravity［C］∥Proceedings of the 45th Conference on Decision and Control.San Diego，CA，US：IEEE，2006：1635-1640.

［6］ 趙林輝，劉志遠，陳虹.一種車輛狀態滑模觀測器的設計方法［J］.電機與控制學報，2009，13（4）：565-570. ZHAO Lin-hui，LIU Zhi-yuan，CHEN Hong.Design method of sliding model observer for vehicle state［J］.Electric Machines and Control，2009，13（4）：565-570.（in Chinese）

［7］ 丁能根，李丹華，余貴珍.基于卡爾曼濾波和ABS控制輸入的車速估計［J］.北京航空航天大學學報，2011，37（1）：67-71. DING Neng-gen，LI Dan-hua，YU Gui-zhen.Estimation of vehicle speed based on Kalman filter and ABS control inputs［J］.Journal of Beijing University of Aeronautics and Astronautics，2011，37（1）：67-71.（in Chinese）

［8］ Castro R，Araújo R E，Freitas D.Wheel slip control of EVs based on sliding mode technique with conditional integrators［J］.IEEE Transactions on Industrial Electronics，2013，60（8）：3256-3271.

Method of Vehicle Speed Estimation Adapted in All Conditions for All-wheel Independent Drive Vehicle

YANG Gui-bing，LI Chang-bing，LIAO Zi-li，MA Xiao-jun，LIU Chun-guang
（The Key Lab of All-Electric Technology of Land Warfare Platform，Academy of Armored Force Engineering，Beijing 100072，China）

A speed estimating method adapted in all conditions based on the parameter adaptive Kalman filter is established for speed estimation of the all-wheel independent drive vehicle.The left and right sides are estimated separately，and the parameters of filter are adaptively adjusted by fuzzy controller.An adaptive switching condition is designed based on drive condition and road adhesion condition.The accelerating integral is chosen when the anti-slip of the tire is higher than the preset default value.The effectiveness and accuracy of the speed estimating method are verified through hardware-in-loop real-time simulation.The simulation results show that the proposed method possesses high estimation precision under many operating condistions，and has general application value.

control science and technology；vehicle speed estimation；Kalman filter；adaption of all conditions；all-wheel drive

TJ81

A

1000-1093（2015）10-2006-06

10.3969/j.issn.1000-1093.2015.10.025

2014-12-24

軍隊科研項目（40402050101）

陽貴兵（1987—），男，博士研究生。E-mail：ygb1987@163.com；李長兵（1971—），男，副教授，博士生導師。E-mail：li3690@vip.sina.com