基于排隊理論的制造單元構(gòu)建與加工路徑選擇*

李 翔，周建偉，張雪麗，李忠學(xué)

(蘭州交通大學(xué)機電工程學(xué)院，甘肅蘭州 730070)

0 引言

單元制造是成組技術(shù)(GT)在制造領(lǐng)域中的一個重要應(yīng)用。單元制造系統(tǒng)在減少加工成本與物料搬運成本、縮短任務(wù)期、實現(xiàn)集中管理等方面體現(xiàn)出很大的優(yōu)勢。目前單元制造系統(tǒng)的研究主要包括:單元構(gòu)建、單元布局設(shè)計與單元管理三方面［1］。

設(shè)備組與零件族是單元構(gòu)建的兩個重要因素，針對單元構(gòu)建問題，國內(nèi)外學(xué)者提出了很多數(shù)學(xué)模型。用于構(gòu)建單元的目標(biāo)規(guī)劃模型主要是基于成本最優(yōu)原則［2-4］，劃分的單元塊與選定的工件加工路徑能夠保證較低的加工成本與物料搬運成本，但由于在建立模型時并沒有考慮加工系統(tǒng)中存在的排隊現(xiàn)象，會導(dǎo)致某種設(shè)備前有排隊而某種設(shè)備卻一直閑置的問題，這不僅會增加后續(xù)的設(shè)備維修費用，而且設(shè)備負荷強度不均衡則不能保證相近的零件加工進度，不但對企業(yè)是一種資源的浪費，也會增加生產(chǎn)管理難度。Buzacott等［5］提出用排隊理論將具有相似加工時間的零件分配到同一單元，使單元便于生產(chǎn)管理。Arghis等［6］運用排隊理論建立了減少閑置成本與等待成本的單目標(biāo)規(guī)劃數(shù)學(xué)模型。

筆者借鑒Buzacott和Arghis運用排隊理論的建模方法，將每臺設(shè)備看作是一個M/M/1排隊系統(tǒng)，整個系統(tǒng)等效為一個開環(huán)排隊網(wǎng)絡(luò)模型。模型中的工件具有多種加工路徑，優(yōu)化加工成本與等待成本的同時，削弱排隊影響、均衡設(shè)備服務(wù)強度與單元服務(wù)強度，最終實現(xiàn)單元構(gòu)建與工件加工路徑選擇。

1 理論基礎(chǔ)

1．1 排隊基本原理

排隊在生產(chǎn)實際中是一種常見的現(xiàn)象，例如車間中在機床邊等待加工的零件。在排隊理論中，把要求服務(wù)的對象統(tǒng)稱為“顧客”，把提供服務(wù)的人或機構(gòu)稱為“服務(wù)臺”。一個排隊系統(tǒng)有3個基本組成部分:輸入過程、排隊規(guī)則和服務(wù)機構(gòu)，本文中的排隊系統(tǒng)采用M/M/1形式，即到達過程是泊松過程，服務(wù)時間服從負指數(shù)分布的單服務(wù)臺排隊系統(tǒng)［7］。在構(gòu)建單元前，首先將多種設(shè)備組成的整個加工系統(tǒng)看作一個服務(wù)臺，如圖1所示，則整個系統(tǒng)構(gòu)成一個M/M/1排隊模型。假設(shè)存在i種零件，每種零件的到達率是λi，則對整個加工系統(tǒng)而言，零件的到達率是:

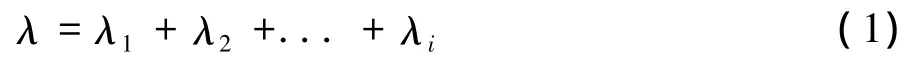
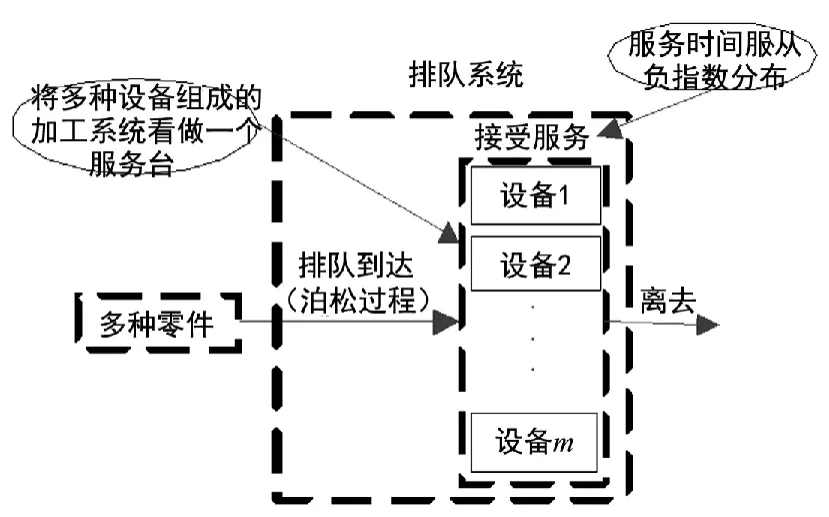
圖1 系統(tǒng)排隊模型

1．2 排隊網(wǎng)絡(luò)

一個排隊網(wǎng)絡(luò)是一些節(jié)點的集合，作業(yè)在這些節(jié)點間移動并接受服務(wù)。每一個節(jié)點從其本身而言都是一個排隊系統(tǒng)。開環(huán)排隊網(wǎng)絡(luò)是指既有到達網(wǎng)絡(luò)的顧客流又有向網(wǎng)絡(luò)外部輸出的顧客流。當(dāng)把每一臺設(shè)備看作是一個節(jié)點時，工件在一個節(jié)點接受服務(wù)后，可以離開網(wǎng)絡(luò)或者去下一個節(jié)點繼續(xù)接受服務(wù)，整個系統(tǒng)就構(gòu)成一個Jackson開環(huán)網(wǎng)絡(luò)模型［8］。

每個節(jié)點n的總體到達率λn是外部到達率λn'和網(wǎng)絡(luò)內(nèi)部到達率之和。對任意節(jié)點m=1，2，．．．，M，作業(yè)在節(jié)點m接受服務(wù)后到節(jié)點n繼續(xù)接受服務(wù)的概率是pmn。根據(jù)定理:M/M/1隊列的離去過程也是泊松過程，這個過程與到達過程相同［］。即離開節(jié)點m的離開率與到達率λm相等。因此有:

1．3 排隊系統(tǒng)的經(jīng)濟分析

排隊現(xiàn)象在加工制造系統(tǒng)中的存在是必然的，但以完全消除排隊現(xiàn)象為研究目標(biāo)是不合理的，這會造成設(shè)施的嚴(yán)重浪費。從經(jīng)濟成本角度考慮，排隊系統(tǒng)中的費用包括服務(wù)費用與等待費用。前者是服務(wù)水平的遞增函數(shù)，后者是服務(wù)水平的遞減函數(shù)，如圖2所示。文中優(yōu)化的目標(biāo)之一是使兩者的費用之和最小，即:

式中:Cm是服務(wù)費用;Cw是等待費用。

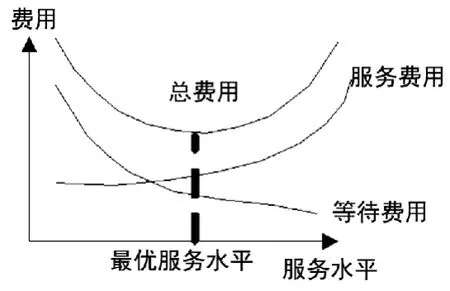
圖2 排隊系統(tǒng)經(jīng)濟模型

2 數(shù)學(xué)模型

基于排隊理論的單元構(gòu)建模型滿足下述假設(shè)條件:①工件與設(shè)備滿足M/M/1排隊模型的要求;②每種工件至少存在一種加工路徑即r≥1，加工之前須指定特定的加工路徑;③加工工序先后順序不會對構(gòu)建單元產(chǎn)生影響;④零件種類與設(shè)備種類已知;⑤在同一設(shè)備上完成不同工件的加工所需時間相同，且每種設(shè)備的服務(wù)率與單位時間運行費用已知;⑥設(shè)備前的單位時間等待費用有兩種，分別是本單元內(nèi)的工件排隊時的單位時間等待費用與其它單元內(nèi)的工件排隊時的單位時間等待費用，兩種費用均不受單元內(nèi)與單元間布局形式的影響。

模型具體形式如下:

令:i為工件編號，i=1，2，．．．，P;j為設(shè)備編號，j=1，2，．．．，M;k 為單元編號，k=1，2，．．．，C;r為加工路徑編號，r=1，2，．．．R;vj為設(shè)備 j的單位時間運轉(zhuǎn)費用;μj為設(shè)備j單位時間內(nèi)可完成的同類操作數(shù)目，即設(shè)備j的服務(wù)率;λj為工件到達設(shè)備j的到達率;λi為工件 i的到達率;ρj為設(shè)備 j的服務(wù)強度;ρk為單元k的服務(wù)強度;Wj為設(shè)備j前的平均等待時間;Wj'為工件在設(shè)備j的排隊系統(tǒng)中的逗留時間;ν，ν'為設(shè)備前的兩種單位時間等待費用，且 ν＜ν';αirj為工件i在路徑r下是否需要設(shè)備j上加工，如果需要則αirj=1，反之為零;Mmax為一個單元內(nèi)的最大設(shè)備數(shù)目;Mmin為一個單元內(nèi)的最小設(shè)備數(shù)目;Pmax為一個單元內(nèi)可加工的最多工件數(shù);Pmin為一個單元內(nèi)可加工的最少工件數(shù);ρjmax為設(shè)備j的最大服務(wù)強度;ρjmin為設(shè)備j的最小服務(wù)強度;ρkmax為單元k的最大服務(wù)強度;ρkmin為單元k的最小服務(wù)強度。

決策變量:

xik:如果工件分配到單元k內(nèi)，則xik=1，其它等于0。

yik:如果設(shè)備分配到單元k內(nèi)，則yik=1，其它等于0。

zir:如果工件i選擇路徑r加工，則zir=1，其它等于0。

目標(biāo)函數(shù)有:

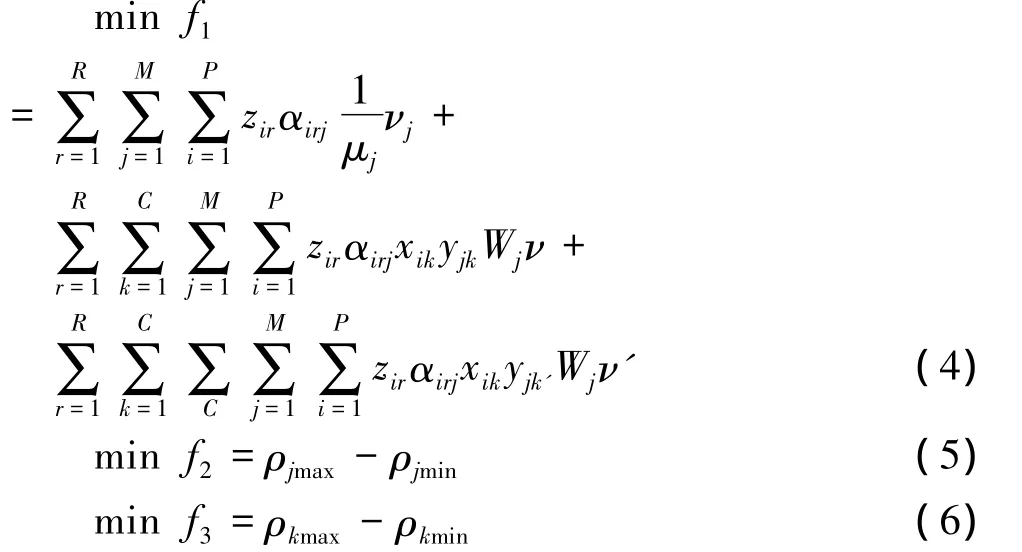
式(4)中，第一部分是工件的加工成本，第二部分與第三部分是排隊費用，其中zirαirjxikyjk表示工件i與在加工路徑r下需要的設(shè)備j在同一單元內(nèi)，zirαirjxikyjk'表示工件i與在加工路徑r下需要的設(shè)備j不在同一單元內(nèi)。式(5)表示最小化設(shè)備服務(wù)強度范圍，式(6)表示最小化單元服務(wù)強度范圍。

約束:

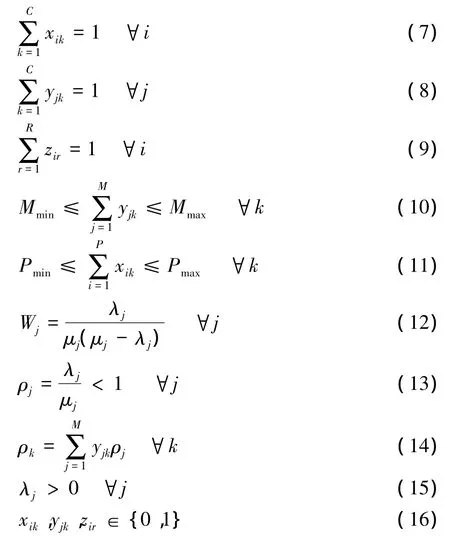
在上列約束中，式(7)和式(8)限制每種工件和設(shè)備只能屬于唯一的單元;式(9)保證每種工件只能選擇一種加工路徑;式(10)表示單元大小限制;式(11)表示單元加工能力限制;式(12)計算任意設(shè)備前的排隊時間，其中根據(jù)式(1)、(2)和假設(shè)(2)可得:

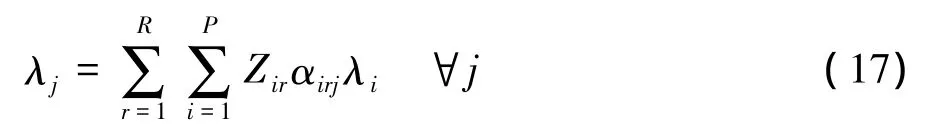
式(13)表示設(shè)備負荷強度約束;式(14)計算單元負荷強度;式(15)表示不能有設(shè)備始終閑置;式(16)決策變量域約束。

將三個目標(biāo)函數(shù)利用線性加權(quán)和法構(gòu)造成一個評價函數(shù)，多目標(biāo)函數(shù)轉(zhuǎn)化為單目標(biāo)優(yōu)化問題。加權(quán)因子分別為 ω1、ω2、ω3，構(gòu)造的評價函數(shù)如下:

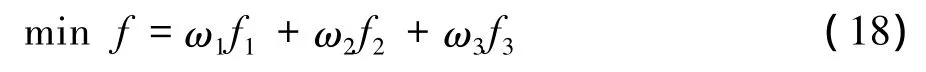
3 算例

為了檢驗上述模型的有效性，隨機選擇如下數(shù)據(jù):有10種分別有兩種加工路徑的工件與10種設(shè)備，工件-設(shè)備原始矩陣如表1所列，表中前一列數(shù)據(jù)表示加工路徑1，后一列數(shù)據(jù)表示加工路徑2;工件的到達率如表2所列;設(shè)備服務(wù)率及單位時間運行費用如表3所列;設(shè)備前的兩種單位時間等待費用分別取 ν=0．3，ν'=0．7。

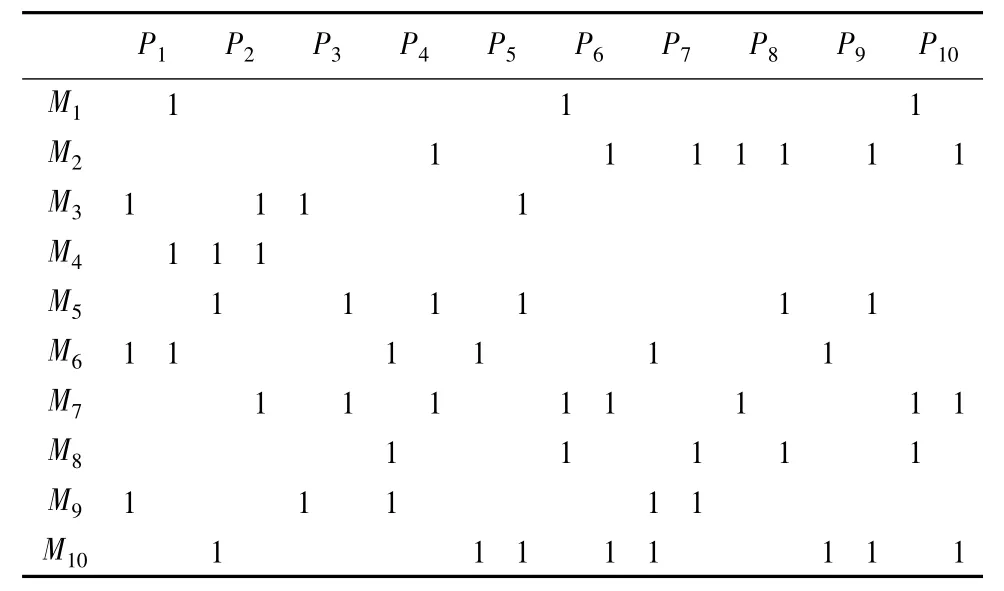
表1 設(shè)備-工件原始矩陣

表2 工件到達率

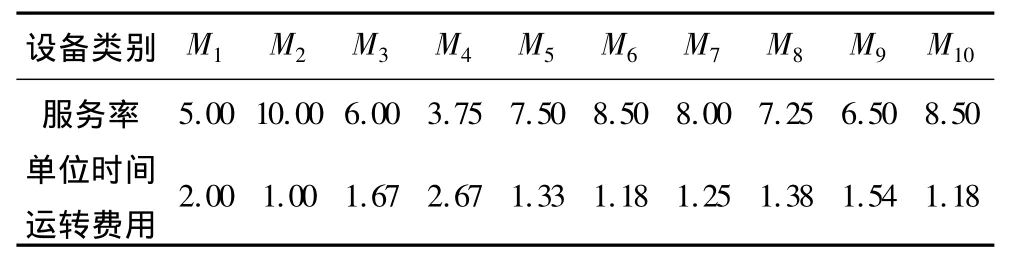
表3 設(shè)備服務(wù)率以及單位時間運轉(zhuǎn)費用

參數(shù)設(shè)置:構(gòu)建3個單元;單元大小限制為:Mmin=2，Mmax=4;單元加工能力限制為:Pmin=2，Pmax=4;加權(quán)因子分別取 ω1=0．5，ω2=0．4，ω3=0．1。筆者采用分枝定界法，在Lingo軟件環(huán)境里對其編程仿真，可以得到一個Pareto解。

實驗結(jié)果:評價函數(shù)值是3．451815;每臺設(shè)備的 Wj、Wj'λj以及 ρj值如表 4;單元構(gòu)建結(jié)果與路徑選擇結(jié)果如表5 所列，工件1、2、3、5、6、8、9 選擇加工路徑1，工件4、7、10選擇加工路徑2;單元服務(wù)強度如表6所列。

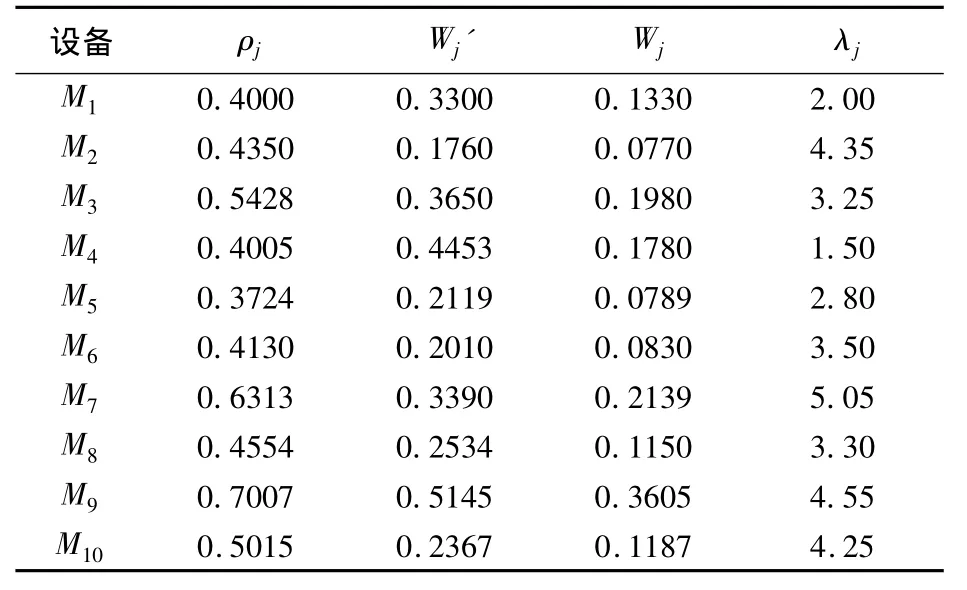
表 4 設(shè)備的 ρj、W j'、W j和 λj值

從圖表4～6可看出，通過該模型能夠較好的構(gòu)建單元并選出加工路徑。通過優(yōu)化設(shè)備服務(wù)強度范圍，工件通過系統(tǒng)的時間也得到了優(yōu)化。單元服務(wù)強度與單元內(nèi)的設(shè)備種類、設(shè)備服務(wù)率、工件種類、工件到達率等息息相關(guān)，通過模型優(yōu)化，三個單元的服務(wù)強度也處于相近的范圍內(nèi)。針對這個算例，筆者通過改變單元數(shù)等相關(guān)等參數(shù)進行了多次求解，結(jié)果表明劃分三個單元時評價函數(shù)值最小。

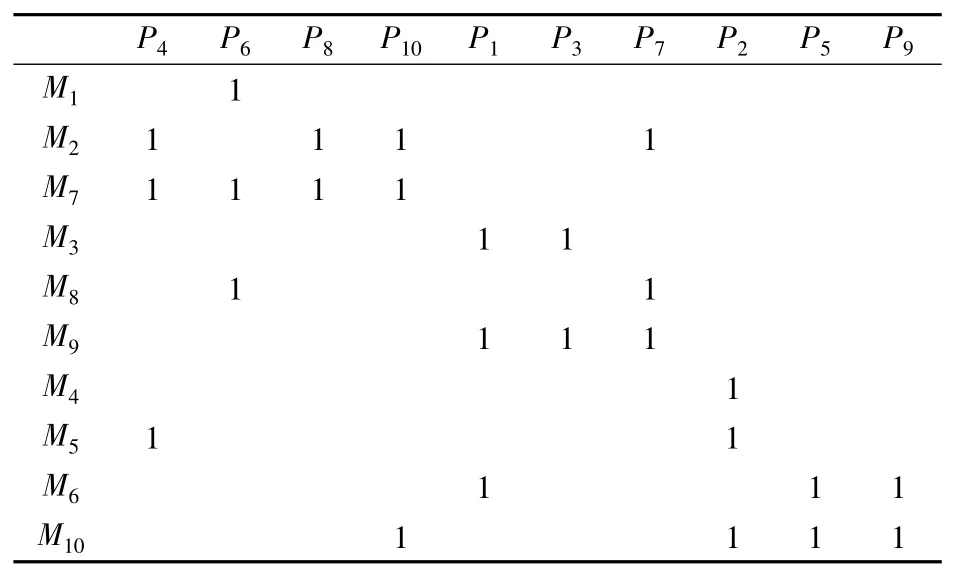
表5 單元構(gòu)建結(jié)果矩陣

表6 單元服務(wù)強度

4 結(jié)語

研究了如何利用排隊理論解決單元制造系統(tǒng)的單元構(gòu)建與工件加工路徑選擇問題。構(gòu)造了以最小化加工成本與等待成本、最小化設(shè)備與單元服務(wù)強度范圍(設(shè)備、單元負荷均衡)為目標(biāo)的多目標(biāo)非線性0-1整數(shù)規(guī)劃模型，采用線性加權(quán)和法將多目標(biāo)問題轉(zhuǎn)換為一個評價函數(shù)，模型求解用分枝定界法。最后在Lingo12平臺上驗證了一個隨機算例，實驗結(jié)果證明該模型能夠?qū)崿F(xiàn)單元構(gòu)建、工件加工路徑選擇、優(yōu)化設(shè)備服務(wù)強度與單元服務(wù)強度的目標(biāo)，達到了預(yù)期效果。

筆者采用的排隊基本模型是M/M/1形式，實際上當(dāng)工件到達分布與設(shè)備服務(wù)時間分布是一般情形時，文中所建模型也同樣適用。但是所建模型是基于不受單元內(nèi)與單元間布局方式的影響假設(shè)，針對這個問題，如何完善模型并應(yīng)用啟發(fā)式算法求解大規(guī)模問題還有待深入。

［1］ 吳曉丹，王云峰，朱昭杰，等．單元制造系統(tǒng)集成建模研究［J］．計算機集成制造系統(tǒng)，2000，6(2):36-40．

［2］ Jabal AmeliM S，Moshref JavadiM．Concurrent Cell Formation and layout Design using Scatter ssearch［J］．International Journal of Advanced Technology，2014，71(1/4):1-22．

［3］ Raminfar R，Zulkifli N，Vasili M，etal．An Integrated Model of Production Planning and Cell Formation in Cellular Manufacturing Systems［J］．Journal of Applied Mathematics，2013:1-10．

［4］ Asgharpour M J，Javadian N．Solving a Stochastic Cellular Manufacturing Model by Using Genetic Algorithms［J］．International Journal of Engineering，Transactions A:Basics，2004，17(2):145-155．

［5］ Buzacott JA，Shanthikumar JG．Design of Manufacturing Systems using Queuing Models［J］．Queuing Systems:Theory and Applications，1992，12(1/2):135-213．

［6］ Arghish O，AzadiS，Anvari A，etal．Cellular Manufacturing System design with Queuing Approach［J］．Journal of Basic and Applied Scientific Research，2012，2(11):11884-11890．

［7］ 熊 偉．運籌學(xué)［M］．北京:機械工業(yè)出版社，2005．

［8］ Salvendy G(著)．鄭 立，李從東(譯)．工業(yè)工程手冊［M］．北京:清華大學(xué)出版社，2005．

［9］ 曾 勇，董麗華，馬建峰．排隊現(xiàn)象的建模、解析與模擬［M］．西安:西安電子科技大學(xué)出版社，2011．