基于風險偏好的區間直覺模糊多屬性決策方法

李 梅,吳 沖,孫明明

(1.哈爾濱工業大學管理學院,黑龍江哈爾濱 150001; 2.廣西師范學院物流管理與工程學院,廣西南寧530001; 3.東北石油大學研究生院,黑龍江大慶 163318)

基于風險偏好的區間直覺模糊多屬性決策方法

李 梅1,2,吳 沖1,孫明明3

(1.哈爾濱工業大學管理學院,黑龍江哈爾濱 150001; 2.廣西師范學院物流管理與工程學院,廣西南寧530001; 3.東北石油大學研究生院,黑龍江大慶 163318)

在多屬性決策中,決策者的風險偏好在很大程度上影響決策結果.根據區間直覺模糊數的特點和多屬性決策的特征,引進風險偏好因子并構建基于風險偏好的區間直覺模糊得分函數,研究其性質及排序規則;結合區間直覺模糊加權平均算子,建立基于風險偏好的區間直覺模糊多屬性決策方法.算例結果表明:該方法能夠很好地體現決策者的風險態度,具有實用性和有效性.

風險偏好因子;區間直覺模糊數;得分函數;多屬性決策

DOI 10.3969/j.issn.2095-4107.2015.05.015

0　引言

Zadeh L A[1]于1965年開創性地提出模糊集概念,為人們處理模糊信息開辟新的領域;Atanassov K等[2-3]提出直覺模糊集和區間直覺模糊集的概念.傳統的模糊集僅考慮隸屬度;直覺模糊集不僅考慮隸屬度,還考慮非隸屬度和猶豫度,在處理不確定問題和模糊信息時,比模糊集具有更強的靈活性.區間直覺模糊集的特點是隸屬度和非隸屬度為區間值,與環境的復雜動態性、決策者知識的有限性等因素適應,因此區間直覺模糊集能夠比直覺模糊集更全面、直觀和細致地刻畫決策者的偏好信息.

近年來,區間直覺模糊集在多屬性決策領域得到廣泛應用.文獻[4]和[5]分別將連續交叉熵和相關系數應用于區間直覺模糊數的比較;文獻[6]對區間直覺模糊信息的TOPSIS多屬性決策方法進行熵權領域的改進;文獻[7]研究區間直覺模糊集的模糊熵群決策方法;文獻[8]將證據推理方法推廣到區間直覺模糊多屬性決策.此外,區間直覺模糊算子[9-10]和相似性測度[11]等方面的研究也得到發展.

在多屬性決策方法中,區間直覺模糊數和直覺模糊數一樣,可以通過得分函數和精確函數進行比較和排序.徐澤水[9]定義區間直覺模糊數的得分函數和精確函數,并將它應用于多屬性決策研究.文獻[12-13]從不同的角度定義區間直覺模糊數的得分函數,并應用于比較排序,充分考慮區間直覺模糊數的猶豫度影響.文獻[14]給出基于模糊熵權重的得分函數和精確函數,解決權重未知環境下區間直覺模糊數比較和排序問題.在多屬性決策過程中,決策者的風險偏好在很大程度上影響決策結果,這些文獻構建的得分函數忽略決策者的風險偏好因素,導致決策結果沒有體現決策者的風險態度.基于區間直覺模糊得分函數,結合決策者風險偏好對風險結果帶來的影響,筆者構建基于風險偏好的區間直覺模糊得分函數,并將它應用于多屬性決策分析.

1　區間直覺模糊集及集結算子

定義1 設X是一個非空集合,則稱

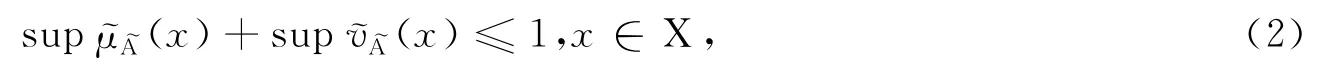
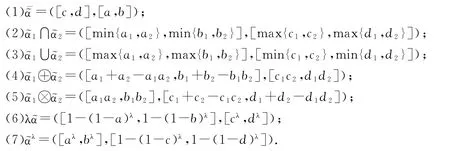
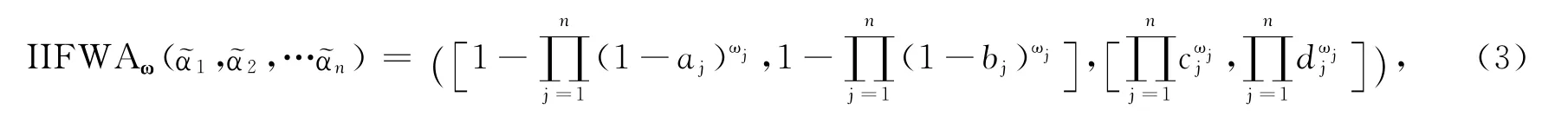
2　改進的區間直覺模糊得分函數

2.1經典區間直覺模糊得分函數和精確函數

徐澤水[9]提出精確函數的概念,并明確比較區間直覺模糊數的基本規則:

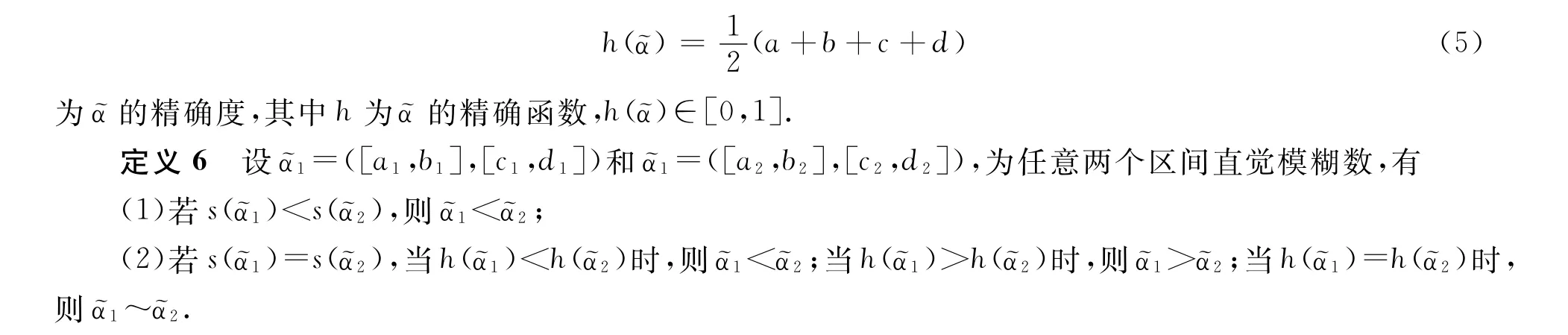
2.2風險偏好區間直覺模糊得分函數

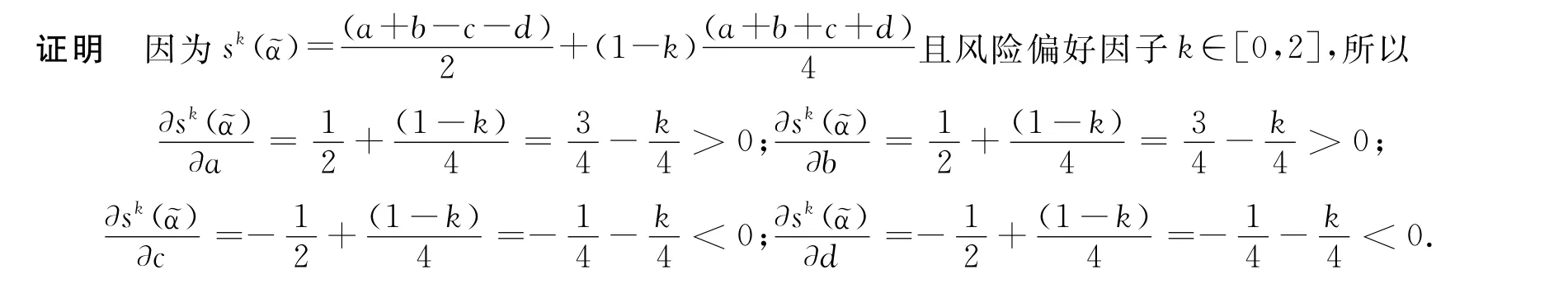
3　決策模型的構建

3.1問題描述

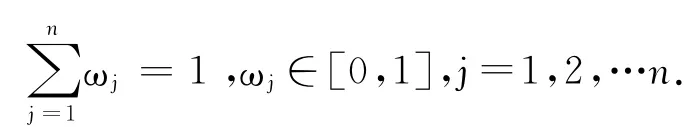
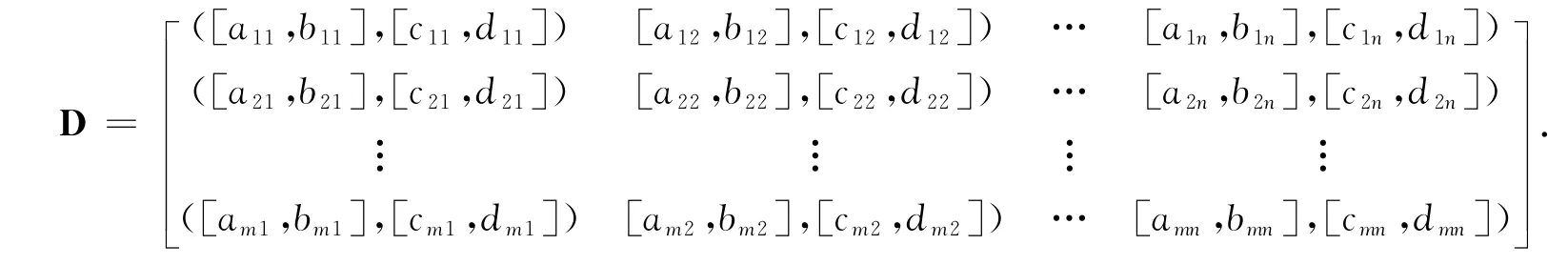
3.2決策步驟

步驟1 獲取決策者的決策信息,包括方案集、屬性集、權重向量和用區間直覺模糊數表達的決策屬性值等信息;

步驟2 利用式(3)的IIFWA算子將多屬性決策信息進行集結,形成方案的區間直覺模糊綜合值;

步驟3 利用式(6)的基于風險偏好的區間直覺模糊得分函數進行方案優選,并分析與其他得分函數結果.

4　算例分析

使用文獻[14]的算例進行分析.某投資公司打算進行一項投資計劃,擬確定的投資對象有5個企業: (1)A1是一個汽車公司;(2)A2是一個食品加工企業;(3)A3是一個計算機軟件公司;(4)A4是一個服裝加工廠;(5)A5是一個武器裝備企業.投資公司在投資時必須考慮要素:(1)C1是風險因素;(2)C2是利潤增長因素;(3)C3是環境影響因素.三個影響因素的權重為ω=(0.21,0.41,0.38)T,決策專家小組根據三個因素對5個擬確定的投資企業進行評價排序,評價結果用區間直覺模糊數集的形式表示出來,決策矩陣D為

在決策矩陣D中,決策值為區間直覺模糊數.如決策值([0.6,0.7],[0.2,0.3])表示決策者認為方案A1滿足屬性C1的程度是0.6～0.7,方案A1不滿足屬性C1的程度是0.2～0.3.

采用基于風險偏好的多屬性決策方法進行決策.首先,利用式(3)的IIFWA算子將多屬性決策信息進行集結,形成方案的區間直覺模糊綜合值,以方案A1為例:

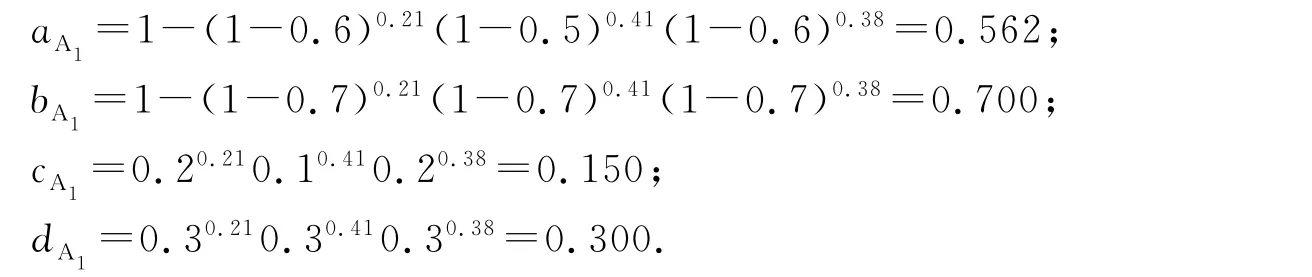
利用文獻[9,12-14]及式(6)基于風險偏好的區間直覺模糊得分函數進行方案優選,結果見表1和圖1.

表1　算例的計算方法及結果排序Table 1 Calculation method and ranking results

由表1可知,文獻[9,13,14]的決策結果為A3＞A1＞A2＞A4＞A5,文獻[12]的決策結果為A1＞A2＞A3＞A4＞A5;通過直覺判斷分析~αA1和~αA2的關系為A3＞A1,顯然,文獻[12]的決策結果與直覺判斷相悖,故在算例中采用文獻[12]的計算方法不合理.

由于文中方法引入風險偏好因子k,當k=2時,即決策者是風險偏好者時,決策結果為A3＞A1＞A2＞A5＞A4;當k=1時,決策者是風險中立者時,決策結果為A3＞A1＞A2＞A4＞A5;當k=0時,決策者是風險厭惡者,決策結果為A3＞A1＞A2＞A4＞A5.文獻[9,13,14]的決策結果和文中方法假定決策者是風險厭惡者和中立者的結論一致,忽視決策者可能存在風險偏好的可能,因而是不完整的.通過圖1結合算例數據分析,k≈1.68是風險偏好因子的臨界值.

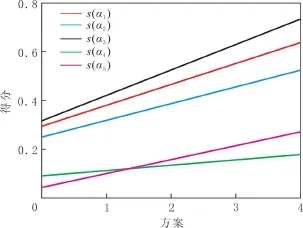
圖1　基于風險偏好的區間直覺模糊決策方法的方案排序Fig.1 Ranking of interval intuitionistic fuzzy decision method based on risk preference

5　結束語

在多屬性決策中,決策者的風險偏好在很大程度上影響決策結果.文中構建基于風險偏好的區間直覺模糊得分函數并將它用于多屬性決策分析,同時證明該函數具有單調性、有界性等及排序規則的正確性.將決策者的風險偏好因子和區間直覺模糊數的隸屬度區間、非隸屬度區間、猶豫度結合,所構建的得分函數能夠彌補經典和派生的得分函數的缺點,對于區間直覺模糊多屬性決策的研究具有一定的意義.

[1] Zadeh L A.Fuzzy sets[J].Information and Control,1965,8(3):338-353.

[2] Atanassov K.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1):87-96.

[3] Atanassov K,Gargov G.Interval-valued intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1989,31(3):343-349.

[4] 李香英.區間直覺模糊連續交叉熵及其多屬性決策方法[J].計算機工程與應用,2013,49(15):234-237. Li Xiangying.Interval-valued intuitionistic fuzzy continuous cross-entropy and its application in multi-attribute decision making[J]. Computer Engineering and Applications,2013,49(15):234-237.

[5] 袁宇,關濤,閆相斌,等.基于區間直覺模糊數相關系數的多準則決策模型[J].管理科學學報,2014,17(4):11-16. Yuan Yu,Guan Tao,Yan Xiangbin,et al.Multi-criteria decision making model based on interval-valued intuitionistic fuzzy number correlation coefficient[J].Journal of Management Sciences in China,2014,17(4):11-16.

[6] 吳沖,萬翔宇.基于改進熵權法的區間直覺模糊TOPSIS方法[J].運籌與管理,2014,23(5):42-47. Wu Chong,Wan Xiangyu.Extended TOPSIS with interval-valued intuitionistic fuzzy information based on advanced entropy-weighted method[J].Operations Research and Management Science,2014,23(5):42-47.

[7] 趙萌,任嶸嶸,李剛.區間直覺模糊集的模糊熵群決策方法[J].運籌與管理,2013,22(5):117-121. Zhao Meng,Ren Rongrong,Li Gang.Method based on fuzzy entropy with interval-valued intuitionist fuzzy set for group decision making[J].Operations Research and Management Science,2013,22(5):117-121.

[8] 王堅強.信息不完全確定的多準則區間直覺模糊決策方法[J].控制與決策,2006,21(11):1253-1256. Wang Jianqiang.Multi-criteria interval intuitionistic fuzzy decision-making approach with incomplete certain information[J].Control and Decision,2006,21(11):1253-1256.

[9] 徐澤水.區間直覺模糊信息的集成方法及其在決策中的應用[J].控制與決策,2007,22(2):215-219. Xu Zeshui.Methods for aggregating interval-valued intuitionistic fuzzy information and their application to decision making[J].Control and Decision,2007,22(2):215-219.

[10] 衛貴武.權重信息不完全的區間直覺模糊多屬性決策方法[J].管理學報,2008,5(2):208-212. Wei Guiwu.A method of interval-valued intuitionistic fuzzy multiple attributes decision making with incomplete attribute weight information[J].Chinese Journal of Management,2008,5(2):208-212.

[11] Xu Z S,Yager R.Intuitionistic and interval-valued intuitionistic fuzzy preference relations and their measures of similarity for the evaluation of agreement within a group[J].Fuzzy Optimization Decision Making,2009,8(2):123-139.

[12] Ye J.Multicriteria fuzzy decision-making method based on a novel accuracy function under interval-valued intuitionistic fuzzy environment[J].Expert Systems with Applications,2009,36(3):6899-6902.

[13] Lakshmana V,Muralikrishnan S,Sivaraman G.Multi-criteria decision-making method based on interval-valued intuitionistic fuzzy sets[J].Expert Systems with Applications,2011,38(3):1464-1467.

[14] 孫貴玲,張建華.IVIFS環境下基于模糊熵和得分函數的多準則決策方法[J].模糊系統與數學,2013,27(1):113-117. Sun Guiling,Zhang Jianhua.Decision-making method based on fuzzy entropy and score function under IVIFSenvironment[J].Fuzzy Systems and Mathematics,2013,27(1):113-117.

C934

A

2095-4107(2015)05-0119-06

2015-09-01;編輯:任志平

國家自然科學基金項目(71271070);高等學校專業綜合改革試點項目(ZG0429)

李 梅(1981-),女,博士研究生,副教授,主要從事模糊數學和決策理論與方法方面的研究.