一種圖像增強的混合算法研究

張龍濤，孫玉秋（長江大學信息與數學學院，湖北 荊州 434023）

為更容易的從圖像中獲取所需要的信息，通常會對圖像進行增強處理，增強其動態范圍及對比度等，使其有更好的視覺效果。在數字圖像處理中，當遇到增加圖像動態范圍，提高對比度的問題時，通常會想到直方圖均衡化。直方圖是多種空間與處理技術的基礎，直方圖均衡化是一種常用的空間域處理技術，經直方圖均衡化處理后，圖像的動態范圍會有所增加，對比度和信息量會有所增強。然而，并不是所有的圖像經直方圖均衡化后都能得到很好的效果，這種方法存在自身的不足，如直方圖均衡化不適合處理灰度呈兩端分布且低灰度區域像素點分布較多的圖像；對圖像的整體效果破壞較大，失真嚴重等。針對上述問題，張懿等［1］提出了一種自適應圖像直方圖均衡算法；陳煒赫等［2］提出動態直方圖雙向均衡化的圖像增強方法；郝峻晟等［3］提出首先將灰度區間分割，然后對每個區間分別進行直方圖局部均衡處理的方法；Wanhyun Cuo等［4］提出了一種直方圖處理的新方法。但這些方法都是改進算法，處理圖像的直方圖，從而達到圖像增強的效果，并沒有提出與其他的方法有效結合處理圖像的方法。為此，筆者結合上述方法，針對其中存在的問題提出了一種簡便且高效的圖像增強的混合算法。

1 直方圖均衡

一幅數字圖像的灰度級范圍為［0，L－1］，則該圖像的直方圖可表示為：

或：

式中，xk表示第k級灰度值（0≤k≤L－1）；nk表示第k級灰度值的像素的個數；M，N分別表示圖像的行數和列數；p（xk）表示第k級灰度值在目標圖像中的頻數，所有分量的和等于1。

通常稱式（2）為歸一化的直方圖。要用直方圖均衡的方法處理一幅圖像，首先要定義一個變換函數。若圖像像素與像素之間的灰度值是連續的，則p（xk）可以看成灰度值xk（隨機變量）的概率密度函數（PDF），將其記為p（x）。

定義變換函數：

式中，x為輸入灰度值；y為輸出灰度值，且為一一對應關系。該函數需要滿足下面2個條件：

1）T（x）在區間［0，L－1］上是一個嚴格單調遞增函數；

2）在區間［0，L－1］上，函數T（x）的值域也為［0，L－1］。

在圖像處理中，通常用下面的函數形式：

式（3）右邊為x的累計分布函數CDF，則：

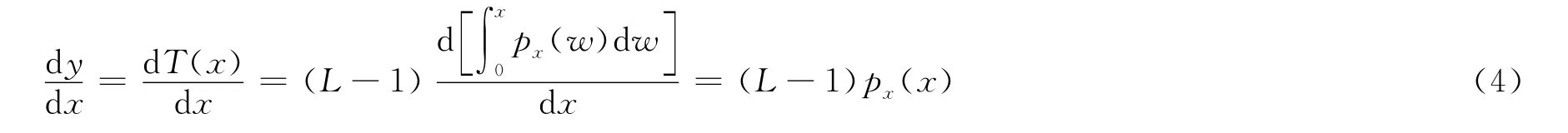
式中，w為積分虛變量。

已知p（x），則可以得到輸出灰度值y的概率密度函數py（y）：

由式（3）、式（4）和式（5）得：

上述方程都是在假設數字圖像的像素灰度值是連續的情況下得到，然而數字圖像的各個像素都是離散的，所以要把上述方程轉化為離散形式。式（3）的離散形式為：

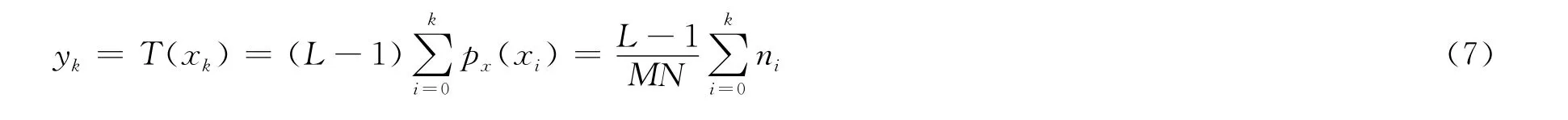
2 梯度銳化

圖像處理中的一階微分使用梯度幅值［5］來實現。函數f（x，y）的梯度為：

式中，gx和gy分別為一階偏微分。

梯度幅度值為：

為便于計算，筆者用絕對值來近似代替求平方及平方根算法，即：

3 灰度擴展

經上述2步處理后的圖像動態范圍可能仍然比較低，為了解決這個問題，還要對經過前2步處理得到的圖像進行灰度擴展：

式中，r表示目標圖像中的像素；min（r）和max（r）分別表示目標函數中的最小灰度值和最大灰度值；h（r）表示輸出灰度值。

因為灰度值是在區間［0，L－1］的正整數，所以在求得h（r）還要對其取整除余得到最終輸出灰度H（r）。

4 試驗結果

選取X射線成像和衛星圖像作為待處理圖像，分別用2種不同的方法以及筆者提出的方法對其進行處理，然后將處理結果進行對比。直方圖是多種空間與處理技術的基礎，可以反映圖像的灰度分布情況。通過觀察一幅圖像的直方圖，可以很直觀的觀察該圖像動態范圍和對比度的高低以及圖像灰度級的分布情況。所以，筆者不但給出了原圖及處理后的圖像，還給出了相應圖像的直方圖。

4.1 X光圖像

圖1（a）是一副人體的胸透圖［5］，因為圖像總體灰度偏低，而且比較模糊，細節觀察不清，所以需要對其進行圖像增強處理。圖1（b）在頻率域是用高頻強調濾波的方法對圖1（a）處理后的結果，可以發現，圖像增強結果并不明顯；圖1（c）是對圖1（a）用直方圖均衡處理的結果，雖然總體灰度有所提高，動態范圍和對比度有所加強，但是圖像細節仍然不易觀察；圖1（d）是用筆者提出的方法對圖1（a）處理后的結果，可見圖像的總體灰度得到提高，動態范圍和對比度得到加強，同時圖像的細節也清晰可見，比前2種處理方法的得到的結果有明顯的提高。

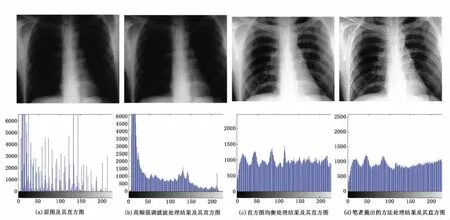
圖1 X光圖像及其處理結果

4.2 衛星圖像

圖2（a）是一副衛星圖像，通過圖像本身和其直方圖可以發現，該圖像總體灰度偏低，而且動態范圍和對比度較小，經直方圖歸一化、直方圖均衡并灰度拉伸和筆者提出的方法分別處理，分別得到圖2（b）、圖2（c）和圖2（d）。

通過觀察不難發現，筆者提出的方法處理原圖像得到的結果比其他2種方法處理得到的結果都要好，不但總體灰度有所改變，動態范圍和對比度有所提高，而且圖像細節也更加明顯。

下面，筆者分別用4鄰域對比度、8鄰域對比度、平均灰度和方差4個參數對圖1、圖2及其處理后的圖像分別進行對比，對比結果分別如表1、表2所示。從對比結果可見，筆者提出的算法可以顯著提高圖像對比度。對于整體灰度較低的圖像，該算法還可以提高圖像整體灰度，從方差對比結果來看，經該算法處理后，圖像質量得到顯著提高。

圖2 衛星圖像處理結果和各個圖像的直方圖

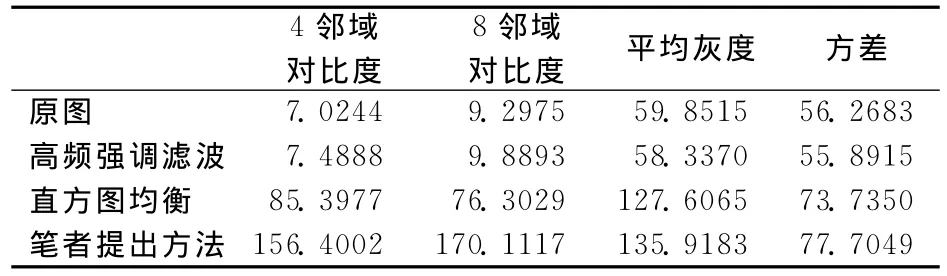
表1 圖1結果對比

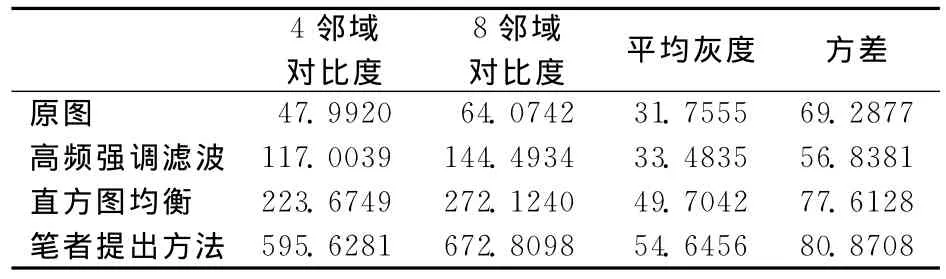
表2 圖2結果對比

5 結語

針對單一處理方法中存在的缺陷，如直方圖均衡化后圖像失真，細節增強不夠等不足，提出了一種基于直方圖均衡化、梯度銳化和灰度擴展的混合方法。通過對圖像的處理試驗證明，經過該混合方法處理后的圖像，其動態范圍和對比度的提升都比用單一的方法處理后的效果要好，而且細節增強明顯。另外，該混合算法計算量小，簡單有效，而且用軟件實現簡單。

［1］張懿，劉旭，李海峰.自適應圖像直方圖均衡算法［J］.浙江大學學報（工學版），2007，41（4）：630～633.

［2］曾煒赫，楊俊煒，邢宇翔.動態直方圖雙向均衡化的圖像增強方法［J］.中國體視學與圖像分析，2014，19（2）：129～139.

［3］郝峻晟，戚飛虎.一種直方圖局部均衡的新算法［J］.中國圖像圖形學報，2003，8（A）：13～17.

［4］Wanhyun Cuo，Seongchae Seo，Jinho You，et al.Enhancement Technique of Image Contrast using New Histogram Transformation［J］.Journal of Computer and Communications，2014（2）：52～56.

［5］Rafael C G，Richard E W.數字圖像處理［M］.第3版.北京：電子工業出版社，2011.

［6］Rafael C G，Richard E W，Steven L E.數字圖像處理（MATLAB版）［M］.北京：電子工業出版社，2013.

［7］茆詩松，程依明，濮曉龍.概率與數理統計教程［M］.北京：高等教育出版社，2010.

［8］Mohammad A A Al－Rababah，Abdusamad Al－Marghilani，Mohammed M Al－Shomuani，et al.Adaptive Enhancement Techniques for Solar Images［J］.Journal of Signal and Information Processing，2013（4）：359～363.

［9］Wei jie，Wang Dada，Wang Yanwei，et al.Industrial X－Ray Image Enhancement Algorithm Based on AH and MSR［J］.Engineering，2011（3）：1040～1044.

［10］李繪卓，范勇，唐俊，等.一種非線性變換的雙直方圖紅外圖像增強方法［J］.計算機工程與應用，2014，50（9）：155～159.