基于聚類分析的降階模型在低滲透油藏數值模擬中的應用

張艷玉，李威威，陳會娟

（中國石油大學（華東）石油工程學院，山東青島 266580）

文章編號：1001?246X（2015）05?0603?07

基于聚類分析的降階模型在低滲透油藏數值模擬中的應用

張艷玉，李威威，陳會娟

（中國石油大學（華東）石油工程學院，山東青島 266580）

基于全隱式法求解考慮低滲透油藏流動過程中啟動壓力梯度影響的二維油水兩相流動數學模型；利用本征正交分解法從獲取的快照中提取基函數，將原模型投影到基函數展成的低維子空間中構造相應的降階模型；考慮到依據等時間間隔獲取的快照的缺陷，利用CVT?Lloyd算法對快照進行聚類分析.實例計算表明：通過本征正交分解法構造降階模型能很好地對原模型進行近似；通過基于聚類分析處理快照后，一方面減少數據冗余，生成空間分布更均勻的快照集合從而提高降階模型的精度，另一方面過少的聚類數可能導致快照信息的缺失，影響最后模型的精度.

低滲透油藏；聚類分析；降階模型；本征正交分解

0 引言

根據國內外大量的研究，流體在低滲透介質中的流動不符合達西滲流規律，存在著啟動壓力梯度［1－3］.在油藏數值模擬中由于啟動壓力梯度的引入，使得方程的非線性增強.在利用差分法求解方程的過程中，目前通常采用全隱式法來提高計算的穩定性，但該方法計算量大，求解所需時間較長［4］，為進一步的生產制度優化和歷史擬合造成一定困難.為了解決這個問題，考慮利用模型降階的思想用以加快模擬速度.降階模型是一類有效近似大型系統的方法，近幾年已被成功地應用于許多高新工業技術應用領域.目前本征正交分解法（proper orthogonal decomposition，POD）是構造非線性系統降階模型最流行的方法之一.該方法的基本思想是首先通過實驗或者數值模擬獲取快照并從中提取基函數，而后通過投影法將原始系統的控制方程投影到優選出的少數主要基函數上從而得到相應的降階模型［5－8］.然而快照一般采用等時間間隔法獲取，這樣一來可能出現的問題是快照在空間分布可能不均勻，這意味著有些空間部位的快照數相對集中而其它部位則分布稀疏.2006年，Burkardt［9］引入CVT（Centroidal Voronoi Tesselation）用于構造降階模型的基函數.運用該方法有兩點好處，首先它提供了一個空間上分布更加統一的快照，因此可以有效地減少基函數的個數.其次進行CVT聚類分析后的矩陣在進行奇異值分解（Singular Value Decomposition，SVD）分解時效率更高.2009年，Cardoso［10］將聚類分析用于常規油水兩相滲流的油藏數值模擬，指出通過對快照進行聚類分析可以有效刪除數據的冗余，降低降階模型構造的難度.

本文建立考慮啟動壓力梯度的低滲透油藏二維油水兩相數學模型，并利用全隱式有限差分法對數學模型進行求解，過程中通過本征正交分解（POD）法構造原系統的降階模型加快計算速度，最后通過實例分析計算研究基于POD法的降階模型在低滲透油藏數值模擬中的計算效率以及精度.

1 低滲透油藏數值模擬數學模型

對于低滲透油藏二維油水兩相滲流，根據質量守恒方程建立模型［1］：

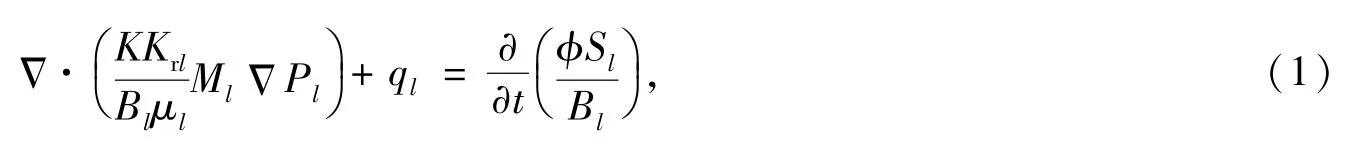
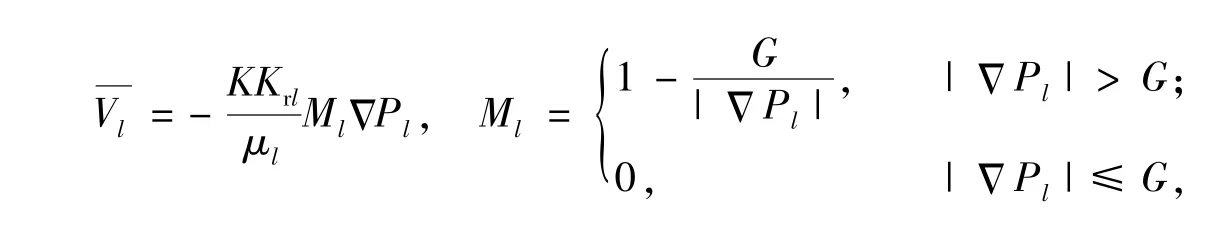
輔助方程

式中，pcow為油水兩相毛管力，0.1MPa.

初始條件

外邊界條件

式中，n為油藏外邊界G的外法線方向.

內邊界條件

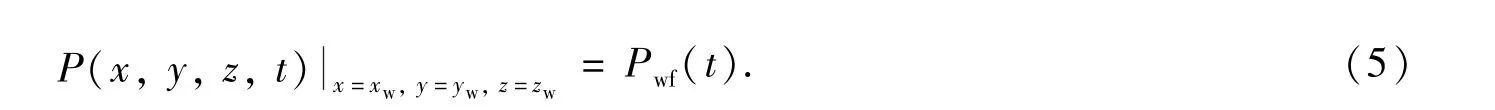
2 數學模型的求解及降階模型的構造

結合式（1）－（5），基于五點差分格式全隱式法進行求解.在構造降階模型的過程中，首先以一定生產制度運行全隱式法求解的模型，以固定時間間隔記錄下模擬過程中每一時刻下各個網格的壓力和飽和度（即快照）［11］，再利用CVT?Lloyd算法對快照進行聚類分析，而后結合本征正交分解法的思想求出基函數，將基函數和全隱式法求解過程相結合，即可得到相應的降階模型，具體過程如下.

2.1 全隱式求解

將方程（1）左右兩端乘以單元體體積VB＝ΔxiΔyjh并引入線性差分算子，簡化方程為

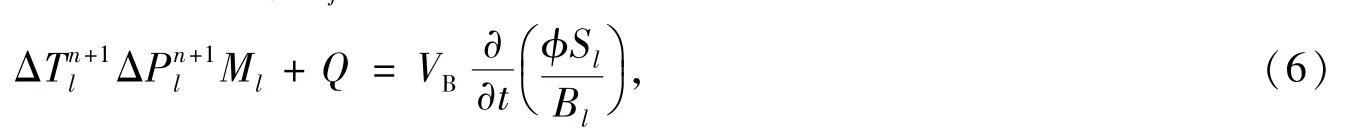
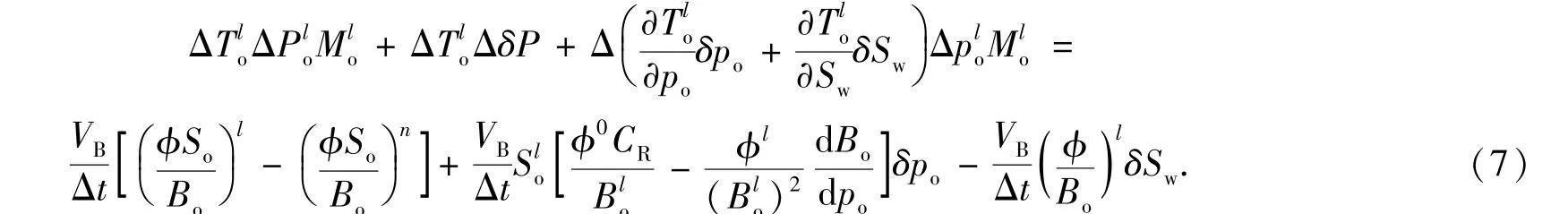
計算過程中流度和啟動壓力梯度按“上游權”選擇［4］，綜合輔助方程（2），水相差分方程表示為

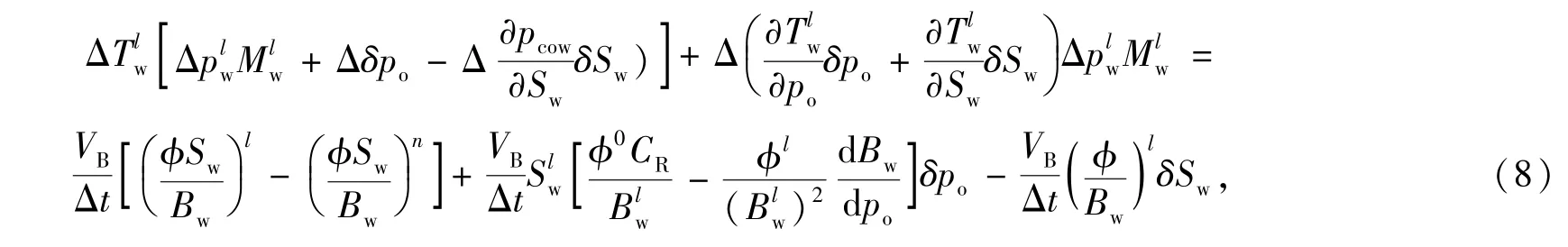
其中，l為每個時間步內的迭代次數；t為時間，s；?0為地層初始孔隙度，無因次；CR為巖石壓縮系數，0.1MPa－1；

產量可以表示為［12－13］

其中，re為Peaceman等效半徑，cm；rw為井眼半徑，cm；pBH為井底流壓，0.1MPa；pe為外邊界壓力，0.1 MPa；Ql為地面條件下產量，cm3·s－1；S為表皮系數；

對定井底流壓條件進行全隱式求解時，油水產量可以分別表示為

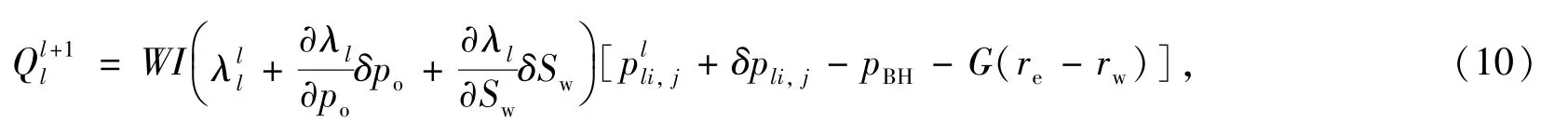
其中，WI＝（2πhKe）/［ln（re/rw）＋S］，λl＝Krl/（Blμl）．

考慮Nc個網格的油水兩相流動，全隱式法求解的具體過程參考文獻［4］，可得

其中，J為雅可比矩陣；δx＝［δpo1，δSw1，δpo2，δSw2，…，δpoNc－1，δSwNc－1，δpoNc，δSwNc］T，

g ＝ ［go1，gw1，go2，gw2，…，goNc－1，gwNc－1，goNc，gwNc］T．

2.2 基于本征正交分解法的降階模型構造

本征正交分解法的基本思想就是將高維空間模型投影到低維空間模型之中.具體來說，首先通過實驗或者計算實例得到的快照構造相關矩陣，利用求得的相關矩陣的特征向量以及對應特征值大小優選出少數正交基函數來刻畫原模型.而后通過將原始模型投影到POD基函數上得到降階模型，從而減少計算過程中的未知數數量［5，10，14］.

2.2.1 獲取快照

由于壓力和飽和度物理性質差異很大，因此將二者分開處理，但處理的過程類似.考慮Nc個網格中油水兩相流動，定義狀態向量：x＝［po1，…，poNc－1，poNc］T或［Sw1，…，SwNc－1，SwNc］T（以下統一用x表示）．按照

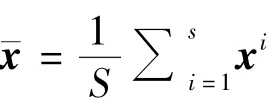
2.2.2 快照的聚類分析

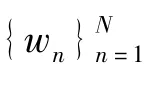
根據以上步驟，將所得質心點集合作為新的快照集合參與下一步運算.

2.2.3 基函數的建立

針對處理后快照形成的矩陣，構造相應的相關矩陣C＝XTX．依據文獻［4］所提出的方法通過直接對X進行奇異值分解可以得到計算相關矩陣C的特征值λ和特征向量Ψ．

基函數可表示為快照的線性組合Φ ＝XΨ．將相關矩陣特征值依次遞減排列，即：λ1≥λ2≥λ3≥λ4….根據文獻［17－18］所述篩選主要的特征基函數，可得壓力保留的基函數個數設為lp，飽和度的基函數個數設為ls．將上一部篩選出的特征值所對應的基函數構成新矩陣Φl，它包含l（l＝lp＋ls?2Nc）列，這樣就將Φ降階至Φl．

2.2.4 將POD基函數和原模型求解過程結合得到降階模型

將降階后的狀態向量定義為z，全階模型下的油水狀態向量x就可以表示為

將（12）式帶入（11），并將等式兩端同時乘以Φl，可得牛頓迭代法的降階表達形式：

3 實例計算

利用某油田區塊實際地質資料建立概念模型對前文所述方法進行驗證.其中基礎數據為：油藏頂部深度1 450m，油層厚度為20m，孔隙度0.3，平均滲透率為0.01μm2，初始含油飽和度0.7，油水啟動壓力梯度為0.0009MPa·m－1.采用五點井網，網格數為Nc＝25×25×1，注水井定井底流壓為14MPa，生產井定井底流壓為9MPa，地層原始壓力為12MPa.

3.1 降階模型的建立

由于從基礎模型中獲取快照的質量直接影響到最后所生成的基函數能否精確反映原模型物理量的變化，此處采用隨機改變生產井井底流壓的生產制度運行程序獲取快照.如圖1所示，對四口生產井（井底流壓相同）每隔1小時隨機改變其井底流壓（但保證其在8.5MPa到9.5MPa之間）并保持該壓力生產一小時，而注入井保持井底流壓為14MPa.

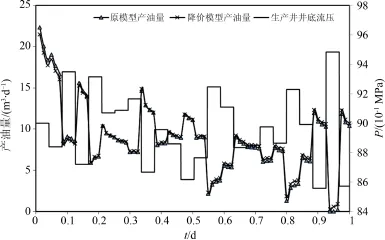
圖1 生產井井底壓力、產水量和產油量隨時間變化Fig.1 Evolution of bottom hole pressure，water production rate and oil production rate

在上述生產制度下，以等時間間隔獲取600張快照，依據CVT?Lloyd算法分別取聚類數為600、500、200、100、50、20和10對快照進行預處理，最后利用上文提出的本征正交分解法構造基函數，最后建立原模型對應的降階模型.對于建立的降階模型，采用基礎模型中使用的生產制度（由于井底流壓隨機改變，因此每種情況具體值都不同），比較原模型和降階模型計算精度.

3.2 結果分析

由圖2可知，整體上經過快照預處理所構造的降階模型對原模型都有較好近似.隨著聚類數的減少，降階模型和原模型在相同生產制度下的偏差逐漸變大.為了進一步定量比較原模型和降階模型的區別，定義降階模型相對原模型的誤差計算公式

其中：ns為快照數；為第i快照時間處原模型產量，cm3·s－1；為第i快照時間處降階模型產量，cm3· s－1；為原模型的平均日產量，cm3·s－1.

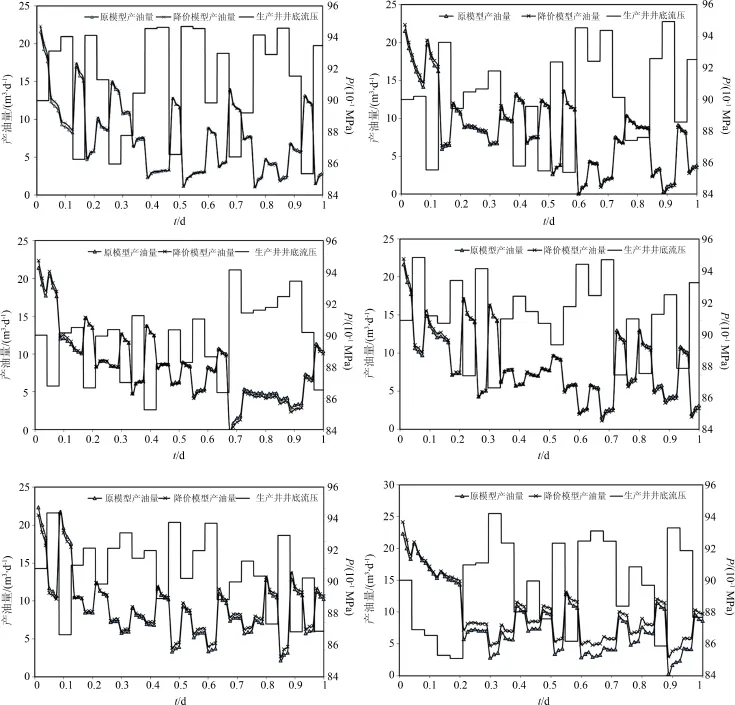
圖2 聚類數為500、200、100、50、20和10時生產井井底壓力和產油量隨時間變化Fig.2 Evolution of bottom hole pressure and oil production rate as number of clusters is set at 500，200，100，50，20 and 10

結合圖2和圖3可知，一方面隨著聚類數進一步減小，模型的誤差不斷增加.另一方面隨著聚類數的增加，模型的誤差也略微增大.產生此現象的原因主要是在獲取快照的過程中，采用間隔固定的時間步長獲取，這樣獲取的在時間上均勻分布的快照可能在空間上不均勻分布.當聚類數不斷減小時，原本不同類型的快照合并導致信息缺失，最終由此構造的降階模型無法有效近似原模型.而當聚類數偏大時，原本相似的快照可能被聚并成多類，那么最終生成的基函數就會倚重某些快照，造成誤差增大.相比于直接利用快照構造降階模型，對快照進行一定大小的聚類一方面可以降低數據的冗余，防止生成的降階模型偏重于某些狀態空間，提高模型的精度，另一方面可以減小相關矩陣維數，從而降低降階模型構造的難度.

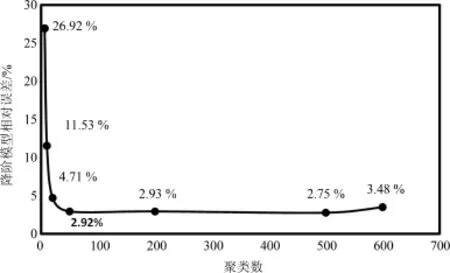
圖3 降階模型誤差隨著聚類數變化Fig.3 Errors of reduced?ordermodel at various numbers of clusters

4 結論

結合全隱式法求解考慮啟動壓力梯度的二維油水兩相滲流模型的基本過程和基于本征正交分解構造降階模型的基本思想，研究了利用聚類分析預處理快照對所構造出的降階模型的影響.研究表明：

1）基于本征正交分解法基本思想所建立的降階模型對原模型有很好的近似，在一定程度上減小了計算量.

2）基于CVT?Lloyd聚類分析處理快照可以有效減小數據冗余從而提高模型精度，但過少的聚類數使得信息缺失，影響降階模型對原模型的近似.

［1］ Huang Yanzhang.Flow mechanism in low permeability oil layers［M］.Beijing：Petroleum Industry Press，1998：93－97.

［2］ Song Fuquan，Liu Ciqun.Analysis of two?phase fluid flow in low permeability reservoir with the threshold pressure gradient ［J］.Journal of the University of Petroleum，China，1999，23（3）：47－56.

［3］ Li Daopin.Development of low permeability reservoir［M］.Beijing：Petroleum Industry Press，1999：25－30.

［4］ Han Dakuang，Chen Qinlei，Yan Cunzhang.Fundamentals of reservoir simulation［M］.Beijing：Petroleum Industry Press，2001.

［5］ Jiang Yaolin.Methods of reduced?ordermodeling［M］.Beijing：Science Press，2010.

［6］ Quarteroni A，Veneziani A.Analysis of a geometricalmultiscalemodel based on the coupling of PDE’s and ODE’s for blood flow simulations［J］.Multiscale Modeling and Simulation，2003，1（2）：173－195.

［7］ Vermeulen P T M，Heemink A W.Inverse modeling of groundwater flow using model reduction［J］.Water Resources Research，2005，41（6）：1－13.

［8］ Yang Y J，Shen K Y.Nonlinear heat?transfermacromodeling for MEMS thermal devices［J］.Journal of Micromechanics and Microengineering，2005，15（2）：408－418.

［9］ Burkardt J，Gunzburger M，Lee H.POD and CVT?based reduced?order modeling of Navier?Stokes flows［J］.Computer Methods in Applied Mechanics and Engineering，2006，196（1）：337－355.

［10］ Cardoso M A，Durlofsky L J.Use of reduced?ordermodeling procedures for production optimization［J］.SPE Journal，2010，15（2）：426－435.

［11］ Sirovich L.Turbulence and the dynamics of coherent structures part I?III［J］.Quarterly of Applied Mathematics，1987，45 （3）：561－590.

［12］ Zhang Bo.Research on numerical simulation of low permeability［D］.Qingdao：China University of Petroleum（East China），2011.

［13］ Wang Jianzhong，Yao Jun，Wang Wei.Numerical simulation of oil?water two?phase flow in low permeability reservoirsconsidering well?grid influence［J］.Journal of Southwest Petroleum University，2013，35（5）：81－86.

［14］ Kunisch K，Volkwein S.Galerkin proper orthogonal decomposition methods for a general equation in fluid dynamics［J］. SIAM Journal on Numerical analysis，2002，40（2）：492－515.

［15］ Li Chengtao，Xiao Yiqing，Ou Jinping.Study on themodel reduction for flexible structure based on clustering algorithm and DOFs concentration［J］.Chinese Journal of Computational Mechanics，2012，29（2）：236－241.

［16］ Hao Pan.A connected area weighted centroidal Voronoi tessellation model for image segmentation［D］.Hangzhou：Zhejiang University，2010.

［17］ Wu Xuehong，Tao Wenquan，Lv Yanli，Gong Yi.Reduced order model for fast computation of incompressible fluid flow problem［J］.Proceedings of the CSEE，2010，30（26）：69－73.

［18］ Wang Zhongxia.Reduced ordermodels based on PODmethod for wind turbine blade design［D］.Beijing：Chinese Academy of Sciences，2011

Reduced?order M odel Based on Cluster Analysis in Numerical Simulation of Low Permeability Reservoir

ZHANG Yanyu，LIWeiwei，CHEN Huijuan
（College of Petroleum Engineering，China University ofPetroleum，Qingdao 266580，China）

A mathematical model for numerical simulation of 2D water?oil phase reservoir concerning start?up pressure gradient is solved with full implicit finite difference scheme.A reduced?ordermodel is established by projecting originalmodel in low dimension space formed by basis functions，which is produced from collected snapshots；CVT?Lloyd algorithm is employed in cluster analysis to tackle with flaws from collecting snapshots of same time interval.Computational results show that reduced?order model established based on POD is able to approximate the originalmodel effectively.With cluster analysis，data reduction is eliminated，which could create uniform snapshots in space resulting in enhanced accuracy of reduce?order model.On the other hand，extremely limited clustering groupsmay lead to loss of information and thus impairing accuracy of reduced?ordermodel.

low permeability reservoir；cluster analysis；reduced?ordermodel；proper orthogonal decomposition；

TE34

A

2014－08－07；

2014－12－28

張艷玉（1963－），女，博士，教授，從事油藏工程的教學和研究工作，E?mail：yyzhang＠upc.edu.cn

Received date： 2014－08－07；Revised date： 2014－12－28