材料熱物性與熱源強度辨識的改進遺傳算法

顏 帆，盧 玫

（上海理工大學能源與動力工程學院，上海 200093）

文章編號：1001?246X（2015）05?0623?08

材料熱物性與熱源強度辨識的改進遺傳算法

顏 帆，盧 玫?

（上海理工大學能源與動力工程學院，上海 200093）

建立二維非線性導熱逆問題（IHCP）的數學模型.通過對基本遺傳算法逐步改進得到三種不同改進階段的遺傳算法，分別用于反演導熱問題中材料的導熱系數及其內部熱源強度，并比較遺傳算法在各改進階段用于求解導熱逆問題時的收斂速度與求解精度，尋求一種使導熱逆問題求解效率與計算精度更高的遺傳算法改進策略.結果表明：提出的遺傳算法改進策略達到了預期目的.

遺傳算法；導熱逆問題；導熱系數；熱源強度

0 引言

近年來導熱逆問題（IHCP）在生物醫學、無損探傷、電子芯片散熱設計等領域運用愈發廣泛.導熱逆問題的求解通常可轉化為一優化問題，由于其具有計算量大、不適定性和非線性等特點，因此選擇一種合適、高效的優化方法對于解決此類反問題非常重要.不少文獻采用傳統梯度類優化方法，如正則化方法［1－2］、共軛梯度法［3－6］等求解導熱逆問題，由于存在模型誤差和觀測誤差，其解常常是振蕩和不收斂的［7－8］，且依賴于初始搜索點［9－10］，當反演由單宗量向多宗量轉變時，導熱逆問題的不適定性和解的不唯一性表現地更加明顯，計算量較單宗量反演時更大，故選擇一個搜索能力強、魯棒性好的優化方法是解決此類問題的有效手段.遺傳算法作為一種智能優化算法，具有較強的全局與局部搜索能力和良好的魯棒性，能較好地避免局部最優且不依賴于初始搜索點［11］，相比于傳統尋優方法，其在非線性、多宗量辨識方面具有優勢.國內外許多學者已將遺傳算法運用于尋優過程，并有學者對遺傳算法采取了一些改進措施.王登剛等人利用遺傳算法反演材料導熱系數時提出保留每代最優個體的策略［12］；王秀春等人對遺傳算法目標函數標定過程進行改進［13］.樂愷等人針對所求問題目標函數具有多峰特征，提出了利用小生境技術提高遺傳算法全局搜索能力［14］.楊偉超等人反演板坯溫度時，考慮求解問題的特殊性，提出采用浮點數編碼的遺傳算法并由此采取針對浮點數編碼的交叉與變異算子［15］.黃長清等人對鋁板帶熱精軋軋制規程優化過程中，對遺傳算法交叉、變異概率進行自適應改進［16］.Raudensky等人采用實數編碼的遺傳算法求解導熱逆問題［17］.Liu為了提高遺傳算法求解時的收斂速度與計算精度，將梯度尋優引入遺傳算法中［18］.

借鑒上述遺傳算法改進措施，通過在遺傳算法中逐步引入價值函數，混沌序列以及擇優選取子代等，分別建立三種處于不同改進階段的遺傳算法，并將其運用于反演材料熱物性與熱源強度的導熱逆問題，旨在獲得一種能提高導熱逆問題求解效率與計算精度的改進遺傳算法.

1 物理問題及數學描述

討論物理對象如圖1所示，截面形狀為矩形，內部有一截面為點的熱源，導熱體的導熱系數λ隨溫度T呈線性變化，并設為λ＝λ0＋aT.由于導熱體長度尺寸遠大于截面尺寸，因此，上述物理問題是一個二維非線性穩態導熱問題，對應的控制方程及邊界條件為

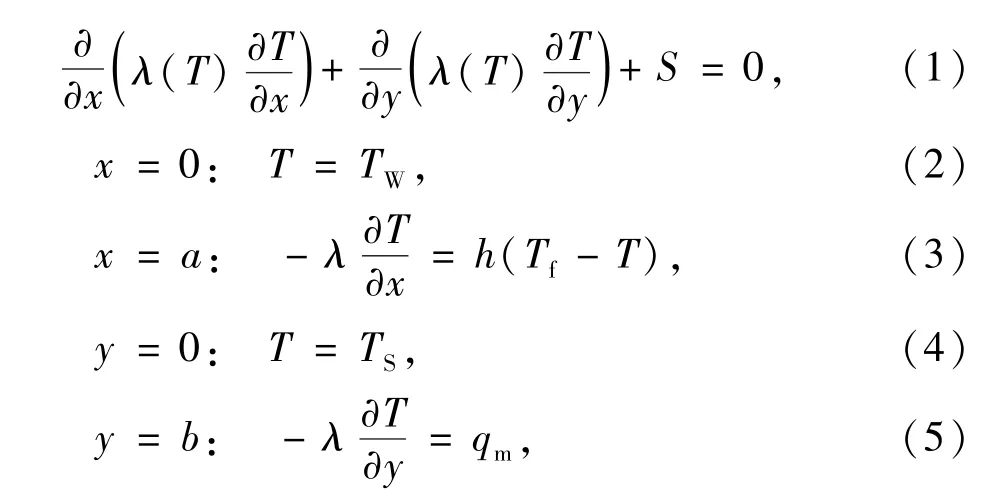
式中T為溫度，K；λ為材料導熱系數，W·（m·K）－1；S為熱源強度，W·m－1；qm為熱流密度，W·m－2；TS為南邊界壁面溫度，K；TW為西邊界壁面溫度，K；Tf為周圍介質溫度，K；h為表面對流換熱系數，W·（m2·K）－1.

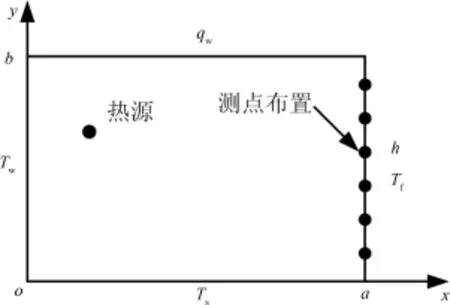
圖1 計算區域示意圖Fig.1 Schematic of calculation area

當材料導熱系數、熱源強度是待定參數時，上述導熱問題即為導熱逆問題，需要附加補充求解條件.本文通過在非第一類邊界條件邊界上布置若干測點（如圖1所示），測量其溫度值對導熱逆問題進行反演求解［19］.定義補充求解條件

式中，Tm為測點處的實測溫度向量.

式（1）、式（2）～（6）構成導熱逆問題的數學描述.定義目標函數［20］

式中，n為測點個數，T為溫度向量的計算值，它依賴于待識別的參數.

定義導熱逆問題的解空間：0≤λ0≤999；0≤a≤0.1；0≤S≤999.利用遺傳算法在解空間中隨機產生一組解：λ0、a與S值，代入式（1）、式（2）～（5）所描述的導熱正問題中求解其溫度場，將對應測點處的計算溫度向量代入式（7），目標函數越小則解越優，故而可轉化為如式（8）所示一全局優化問題

2 遺傳算法

遺傳算法（genetic algorithm，GA）起源于對生物系統所進行的計算機模擬研究，由Holland教授在1967年首次提出.其基本思想是利用某種編碼技術，將所求問題解空間中的可行解轉化為稱為染色體的數字串，通過選擇、交叉、變異等遺傳操作，使可行解逐漸改善，最終獲得最優.

基本遺傳算法可表示為

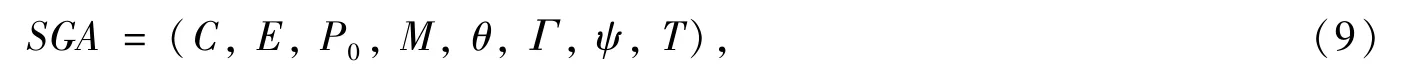
式中C表示個體編碼方式；E表示個體適應度評價函數；P0表示初始種群，M表示種群大小，θ表示選擇算子，Γ表示交叉算子，ψ表示變異算子，T表示算法終止條件.

基本遺傳算法流程圖如圖2所示.

3 改進遺傳算法

上述基本遺傳算法對于導熱反問題的求解僅是概率性收斂［12］.本文首先借鑒目前大多數學者已提出的遺傳算法改進措施，對基本遺傳算法作簡單改進，得到GA?1.在GA?1的基礎上引入價值函數得到GA?2.在GA?2的基礎上再對其進行改進得到GA?3.具體操作過程如下.

GA?1：

1）采用實數編碼；

圖2 遺傳算法基本流程圖Fig.2 Flowchart of GA

2）對由目標函數向適值函數的標定如式（10）：

式中F為適應度函數，f為個體目標函數，fmax與fmin依次為當前代中目標函數值最大與最小的個體，r為小于1的正實數.

3）變異方式上借鑒標準正態分布原理.本文只對被選中進行變異操作基因進行變異操作，以提高算法的局部搜索能力，加速算法的收斂，具體做法為：假設某代種群中一個體可表示為G＝（g1g2g3g4g5g6g7g8），且已選中該個體第三基因位上的基因g3進行變異操作，則其余基因位上基因值不變，第三基因位上基因值變為：＝g3＋N（0，1），式中N（0，1）表示服從標準正態分布的隨機變量.

4）保留每代種群中最優個體.

GA?2：在GA?1基礎上融入如式（11）的價值函數.

式中Jk（gij）表示第k代種群中第i個個體上第j位基因對應的價值函數，gij表示在該代種群中第i個個體上第j基因位上的基因，fij表示對應該個體的目標函數值.其基本思想是計算每代種群中所有個體相同基因位上基因的價值函數，根據這一基因位上基因的價值函數大小進行排序與重組種群.具體操作為：假設第k代種群中有且僅有三個個體，可表示為

若由式（11）計算得到J（g11）＝10，J（g21）＝14，J（g31）＝7，則根據這一基因位上基因的J值大小重組種群得到

第二位基因同理操作，直至最后一位基因.

GA?3：在GA?2基礎上做如下改進.

1）將種群中個體基于價值函數重組操作置于選擇操作之前.選擇方式上采用基于種群中個體適應度值大小進行排序的方法，其基本思想為將種群中所有M個體按適應度值從小到大排序，則排序后第j個個體被選中的概率如式（12）所示.

2）交叉方式上采用擇優交叉，每次交叉均進行N次，在2N個子代中選擇適值最好的兩個個體加入新一代種群；

3）交叉點與變異點的位置利用Logistic混沌序列產生的隨機數來確定.假設第k代種群中兩個體為

取初始值x（0）＝0.3，則x（1）＝4x（0）［1－x（0）］＝0.84，0.84×7＝5.88，取整得6，則第6位作為交叉點，保存此值作為以后確定交叉點的混沌迭代初值.變異操作同理.

三種改進算法在導熱逆問題中求解流程如圖3、4所示.

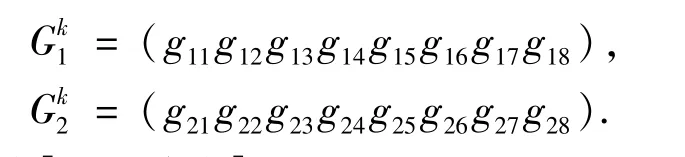
4 計算結果與分析

本文采用數值方法計算求解式（1）、式（2）～（5）所描述的導熱正問題.首先采用有限體積法對圖1所示計算區域進行離散，并引入邊界條件，得到每個網格節點對應的離散方程，所有節點的離散方程構成一非線性方程組.計算中采用逐行法迭代求解方程組，直至收斂后得到整個計算區域的溫度場.

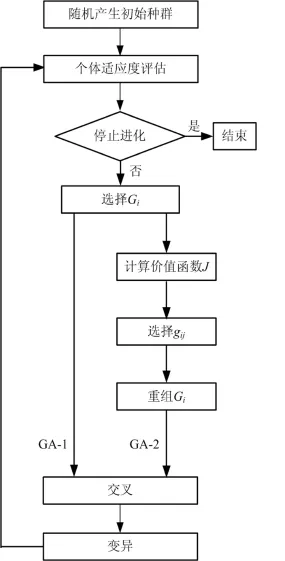
圖3 GA?1與GA?2算法流程圖Fig.3 Flowchart of GA?1 and GA?2

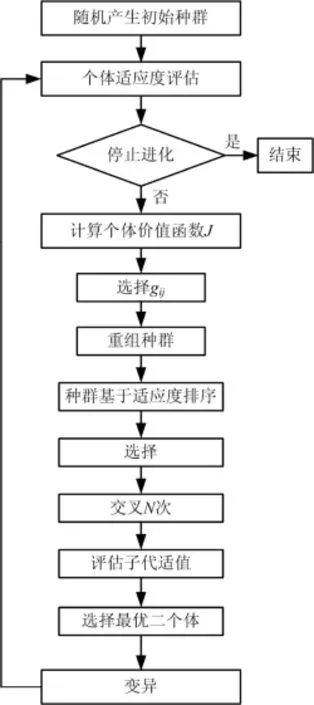
圖4 GA?3算法流程圖Fig.4 Flowchart of GA?3

計算時各參數取值如表1所示.假設該材料真實的導熱系數λ＝500＋0.01T，熱源強度S＝400W·m－1，代入式（1）、式（2）～（5）所示導熱正問題中求解，得到整個計算區域的溫度場，在邊界處選取若干點溫度值，用于代替實際測量值.

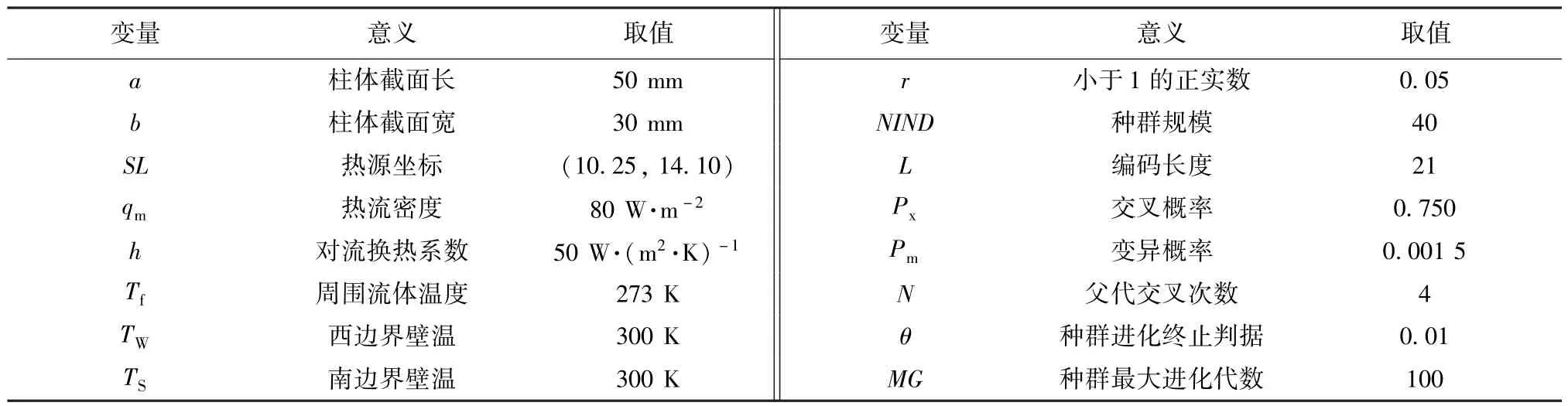
表1 各參數取值表Table 1 Values of parameters

4.1 三種改進遺傳算法反演結果與分析

設定三種改進算法種群進化終止判據均為連續5代種群個體平均適應度之差絕對值小于0.01，同時對最大迭代次數設置限制，限定三種改進算法種群最大進化代數MG均為150，作為終止程序執行的準則.將以上三種算法分別運用于上述導熱逆問題的反演求解，每種算法均進行3次反演計算，計算結果如表2所示.從表中可以看出，GA?3具有最好的求解效率與計算精度，GA?2其次.GA?3是在GA?2基礎上，通過對選擇、交叉等遺傳操作的改進，更好地將優良基因傳遞至下一代，且采用混沌序列使得算法在初始反演階段對解空間的全局搜索能力更強，在計算即將收斂階段收斂速度更快，即算法的全局與局部搜索能力得到了提升.

表2中所列MGA算法是文獻［14］中提出的改進遺傳算法.由表中所列計算結果可以看出，僅作簡單改進的GA?1，雖然克服了概率性收斂問題，但計算效率與精度低于MGA；GA?2雖然求解所需時間略長于MGA，但反演精度高于MGA；而本文最終獲得的改進遺傳算法GA?3，其計算效率與求解精度均明顯優于MGA.

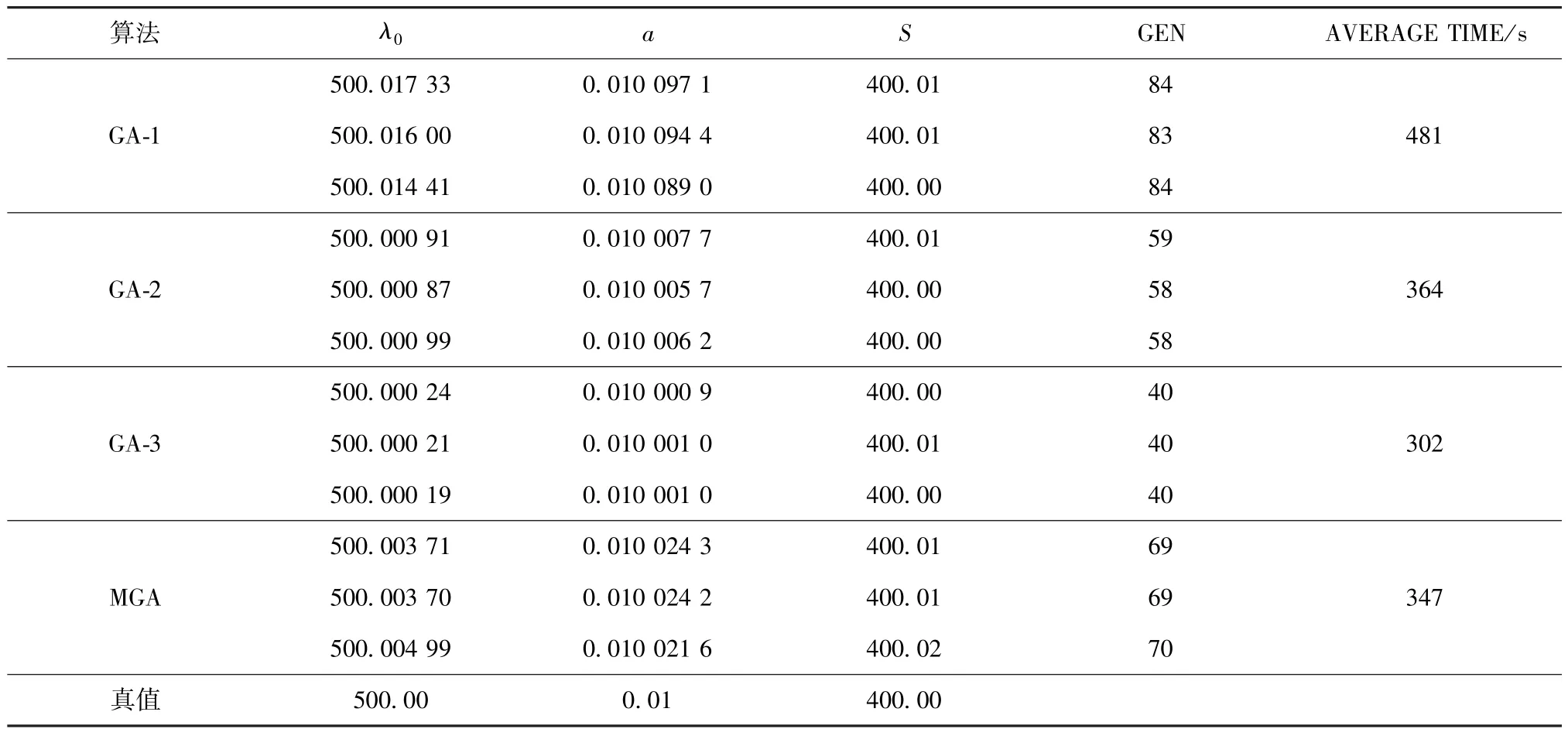
表2 計算結果Table 2 Calcu lation resu lts

為了解各算法在求解逆問題過程中種群進化趨勢，限定三種改進遺傳算法與MGA算法均進行90代種群進化，記錄四種改進算法每代種群中最優個體目標函數值變化趨勢，如圖5.從圖5可以看出，在種群進化代數相同的情況下，GA?3在反演計算中有著最高的求解精度.

GA?3中存在被選擇父代進行N次交叉擇優選擇子代這一操作，對于正整數N的選取，文中進行了驗證，結果如圖6.圖中ηN表示N取某正整數時程序運行時間的倒數.在達到幾乎相同的求解精度情況下，從圖中可知，N取4最優.

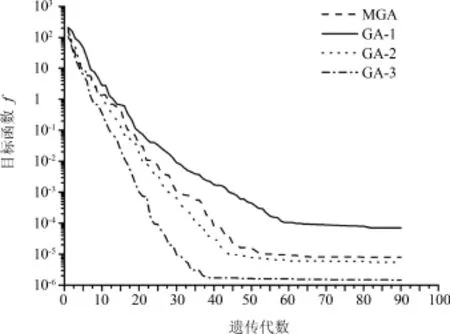
圖5 種群中最優個體目標函數隨代數的變化Fig.5 Objective functions of best individuals in population as functions of generations

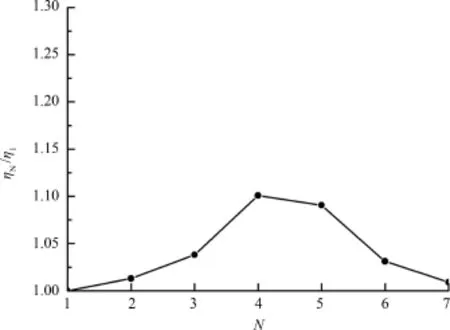
圖6 求解效率隨N取值變化Fig.6 Calculation efficiency as a function of N

4.2 隨機噪聲對算法反演結果的影響

對于以上導熱逆問題的求解，測點溫度是通過求解導熱正問題模擬得到，為模擬測量誤差對計算結果的影響，在沒誤差的正問題的精確解上施加隨機噪聲向量ε，如式（13），以檢測算法在求解問題過程中的抗噪性能.

本文分別給予三種改進算法以3％、6％的隨機噪聲各自進行6次反演計算，用于模擬實際測量中出現的誤差，所得結果如圖7所示，取一次計算結果制成表3.從圖7中可知GA?3抗噪聲性能較GA?2稍好，GA?1抗噪聲性能次于GA?2.

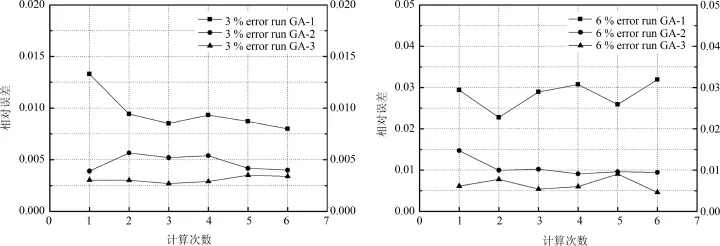
圖7 輸入噪聲對計算結果的影響Fig.7 Influence of input noise on calculation results

表3 加入噪聲反演結果Table 3 Calculation results under input noise

4.3 測點數量及分布對反演結果的影響

在測點布置與數量選擇對導熱逆問題反演結果的影響方面，參照圖8，在計算區域東邊界上均勻設置16個可選測點，在北邊界靠近熱源位置設置3個可選測點，圖中均已標明序號.通過選擇不同數量與位置處的測點，在不考慮噪聲的情況下，采用GA?3算法對文中導熱逆問題進行反演求解，結果如表4所示.

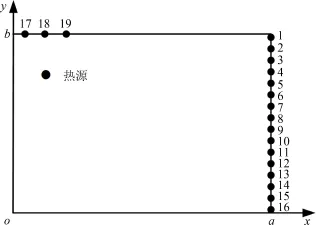
圖8 測點編號示意圖Fig.8 Serial number ofmeasuring points

從表4中可以看出，No.1選擇東邊界上3個測點進行反演計算，所得結果背離了真實值；采取No.5、No.6、No.7的測點數量與分布可反演得到正確的結果，反演精度接近一致且均比采取No.3、No.4時的反演精度要高；No.8有著最好的反演效率與精度.由表4可得出以下結論：（1）測點的布置應適當均勻且應達到一定的數量，同時測點數目并不是越多越好，過多的測點數目只會影響計算效率.（2）測點在數量選擇上可從一個較小的數目開始，逐次遞增，直至相鄰兩次計算結果在一個設定的允許范圍之內，則倒數第二次測點數目為最小觀測點數目.（3）對于文中導熱逆問題，當材料內部存在線狀軸向內熱源且其位置已知，需要對其強度進行反演的情況下，在測點布置方面應盡可能使部分測點靠近熱源均布，測點位置越接近熱源，其上溫度對熱源強度的改變越敏感，越有利于結果的反演.

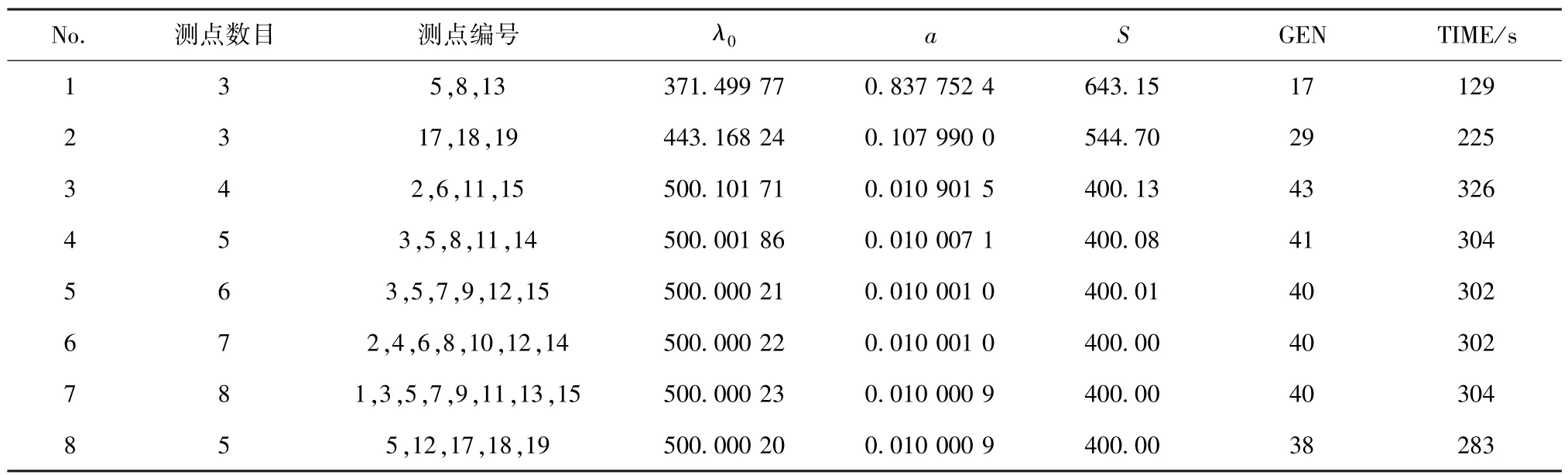
表4 測點數量及分布對最終結果的影響Table 4 Influence ofmeasuring point number and distribution on final results

5 結論

提出三種不同改進階段的遺傳算法，分別對材料導熱系數與熱源強度反演求解.對三種改進方法實例求解的收斂速度、計算精度的分析、比較，得到以下結論：GA?1克服了概率性收斂的問題；GA?2建立在GA?1基礎之上，通過引入價值函數，使得GA?2對導熱逆問題求解的收斂速度、計算精度和抗噪性能較GA?1得到明顯提升；在GA?2基礎上改進得到的GA?3，數值計算結果表明其有著更高地針對導熱逆問題求解的收斂速度和計算精度，同時抗噪性也優于GA?2.

［1］ Lee H S.A new spatial regularization scheme for the identification of the geometric shape of an inclusion in a finite body［J］. International Journal for Numerical Methods in Engineering，1999，46（6）：973－992.

［2］ 王登剛，劉迎曦，李守巨.非線性二維導熱反問題的混沌－正則化混合方法 ［J］.應用數學與力學，2002，23（8）：864－869.

［3］ Huang C H，Ozisik M N，Sawaf B.Conjugate gradient method for determining unknown contact conductance during metal casting［J］.International Journal of Heat and Mass Transfer，1991，34（7）：1779－1785.

［4］ Alifanov OM，Mikhailov V V.Solution of the nonlinear inverse conductivity problem by the iterationmethod［J］.Journal of Engineering Physics，1978，35（6）：1501－1506.

［5］ 俞昌銘.計算熱物性參數的導熱反問題［J］.工程熱物理學報，1982，3（4）：372－378.

［6］ 吳洪潭.二維對流換熱反問題的共軛梯度法求解［J］.宇航計策技術，2005，25（4）：25－27.

［7］ 薛齊文，楊海天.共軛梯度法求解非線性多宗量穩態傳熱反問題［J］.計算力學學報，2005，22（1）：51－54.

［8］ Tervola P.A method to determine the thermal conductivity from measured temperature profiles［J］.International Journal of Heat and Mass Transfer，1989，32（8）：1425－1430.

［9］ 朱麗娜，王廣軍，陳紅.采用共軛梯度法求解多變量穩態傳熱反問題 ［J］.中國電機工程學報，2011，31（8）：58－61.

［10］ 李守巨，劉迎曦.改進遺傳算法在非線性熱傳導參數識別中的應用［J］.工程力學，2005，22（3）：72－75.

［11］ Liu F B.A modified genetic algorithm for solving the inverse heat transfer problem of estimating plan heat source［J］. International Journal of Heat and Mass Transfer，2008，51（15－16）：3745－3752.

［12］ 王登剛，劉迎曦，李守巨，等.非線性二維穩態導熱反問題的一種數值解法［J］.西安交通大學學報，2000，34（11）：49－52.

［13］ 王秀春，智會強，毛一之，等.用遺傳算法求解多維導熱反問題［J］.核動力工程，2005，26（1）：23－27.

［14］ 樂愷，趙琰，張欣欣.改進的遺傳算法在生物組織熱物性參數無損測量中的應用［J］.北京科技大學學報，2008，30（11）：1317－1321.

［15］ 楊偉超，王劍魁，張國山，王赟.基于改進遺傳算法的板坯溫度計算［J］.系統仿真技術，2012，8（4）：259－265.

［16］ 黃長清，劉彬，趙旻，陽康.基于改進遺傳算法的鋁板帶熱精軋軋制規程優化 ［J］.金屬材料與冶金工程，2014，42 （2）：20－24.

［17］ Raudensky M，Woodbury K A，Kral J，Brezina T.Genetic algorithm in solution of inverse heat conduction problems［J］. Numerical Heat Transfer Fundamentals，1995，28（3）：293－306.

［18］ Liu F B.A hybrid method for the inverse heat transfer of estimating fluid thermal conductivity and heat capacity［J］. International Journal of Thermal Sciences，2011，50（5）：718－724.

［19］ Kohn R，Vogelins M.Determining conductivity by boundary measurements［J］.Communications on Pure and Applied Mathematics，1984，137（3）：289－298.

［20］ 黃少君，盧玫，張濤，等.適用于尋源導熱反問題的改進蟻群系統［J］.工程熱物理學報，2013，34（4）：694－697.

M odified Genetic Algorithm for Identifying M aterial
Thermal Properties and Strength of Heat Source

YAN F?an，LU Mei （School of Energy and Power Engineering，University of Shanghai for Science and Technology，Shanghai 200093，China）

A mathematicalmodel for two?dimensional nonlinear inverse heat conduction problem（IHCP）is established.Three kinds of genetic algorithm at differentmodified phase are proposed for identifyingmaterial thermal conductivity and strength of heat source. Convergence speed and calculation precision of genetic algorithms at differentmodified phase are compared.Calculation results show that the genetic algorithm modified strategy proposed achieve higher convergence speed and calculation precision.

genetic algorithm；IHCP；thermal conductivity；strength of heat source

TL329

A

2014－09－25；

2014－12－18

國家自然科學基金（51176126）資助項目

顏帆（1989－），男，碩士，從事導熱逆問題優化方法研究，E?mail：yanfanaust＠163.com

?通訊作者：盧玫（1957－），女，教授，從事導熱逆問題研究，E?mail：rose_luu＠usst.com

Received date： 2014－09－25；Revised date： 2014－12－18