S－分布時滯隨機競爭神經網絡的指數穩定性*

張 燕，楊 彬，王林山

（1.中國海洋大學數學科學學院，山東 青島 266100；2.青島大學，山東 青島 266071）

0 引言

競爭神經網絡是一種無監督學習型神經網絡，在模式識別、信號處理、優化計算和控制理論中有著廣泛應用。從生物學角度出發，人類記憶分為短期記憶（STM）和長期記憶（LTM），STM描述網絡狀態瞬時變化的動力學行為；LTM描述網絡受外部刺激而誘發的無師指導下突觸緩慢變化的動力學行為。由此，文獻［1］提出如下一類具有不同時間尺度的競爭神經網絡：

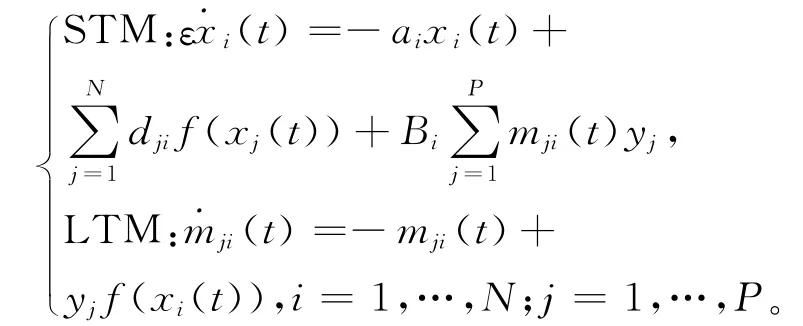
由于神經網絡在運行過程中，神經元之間的突觸反應不可避免地出現時間延遲效應，因此人們研究了含有離散時滯和分布時滯的競爭神經網絡的動力行為［2－4］。特別是，包含離散時滯和分布時滯的S－ 分布時滯的神經網絡動力行為的研究更加引人注目［5－7］。另外，網絡在信號傳輸過程中易受噪聲干擾，噪音往往影響系統的穩定性［8－10］，因此，研究S－ 分布時滯隨機競爭神經網絡的動力學行為不僅是應用的需要，而且理論上也有重要意義。本文研究了一類S－分布時滯隨機競爭神經網絡的適定性和全局指數魯棒穩定性。給出了易于驗證的穩定性判據，推廣了文獻［15-16］中的結果。

1 預備知識

考慮如下S-分布時滯隨機競爭神經網絡模型：

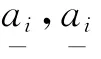
定義 1設x＝（x1，x2，…，xN）T，φ（θ）＝（φ1（t），φ2（t），…，φN（t））∈C（ （－ ∞，0］，RN）和D＝（dij）N×N，則其范數分別定義為：

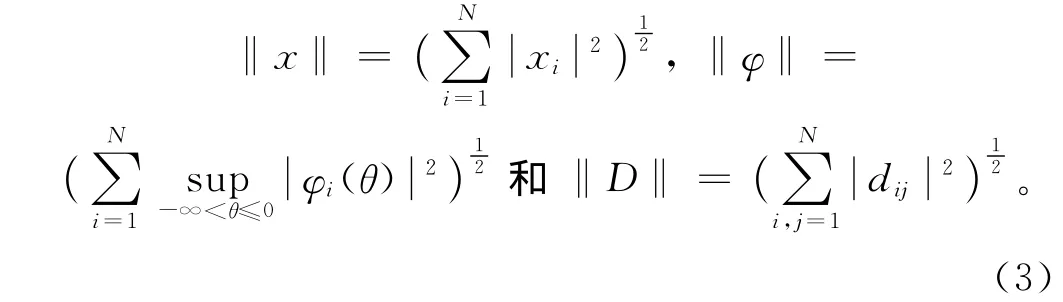
定義2［12］設＝（0，0）T，i＝1，2，…，N為系統（2）的平衡點，對于任意的有界的初始函數φ（θ）＝（φ1（θ），…，φN（θ））T，ψ（θ）＝（ψ1（θ），…，ψN（θ））T∈C（（－ ∞，0］，RN），zi（t）＝（xi（t），Si（t））T是系統（2）滿足條件（t）＝（φi（t），ψi（t））T，i＝1，2，…，N，－∞ ＜t≤0，的解。若存在常數λ＞0，K＞0，使得

則稱系統（2）的平衡點＝（0，0）T，i＝1，2，…，N是全局均方指數穩定的。

定義3［13］如果對每個A∈Al，B∈Bl，C∈Cl，D∈Dl，M∈Ml，且系統（2）的平衡點z＊＝（0，0）T是全局均方指數穩定的，則稱系統（2）在均方意義下是全局指數魯棒穩定的。

引理1［14］考慮完備概率空間 （Ω，｛Ft｝，Ρ） 上的自治泛函微分方程：

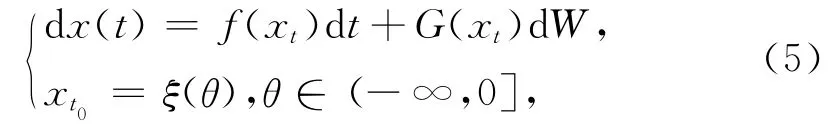
其中：

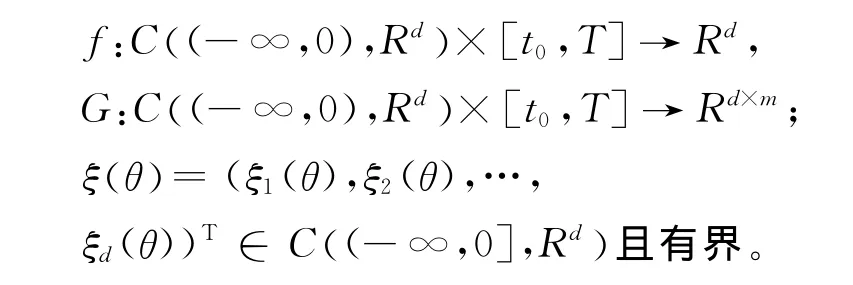
若f，G滿足Lipschitz條件：

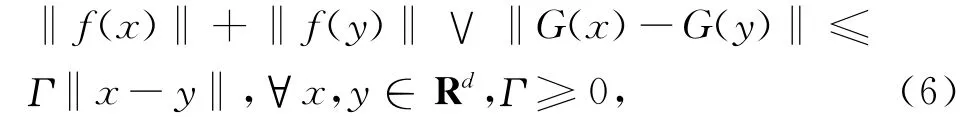
則系統（5）在［t0，T］上存在唯一連續的全局解。

引理2［11］（It定理）令u＝u（t，x1，x2，…，xd）是定義在［t0，T］×Rd上的連續函數且存在連續偏導數ut，uxi，uxixj，i，j＝1，2，…，d，若d維隨機過程xi（t）在［t0，T］滿足：

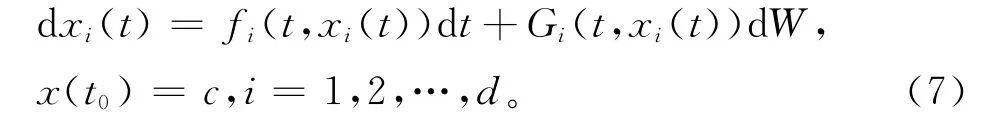
則隨機過程u＝u（t，x1（t），x2（t），…，xd（t））的隨機微分為：

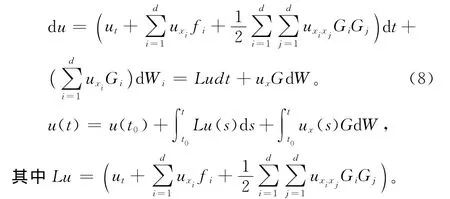
引理3［14］若系統的平衡點在均方意義下是全局指數穩定的，那么網絡是幾乎必然一致指數穩定。

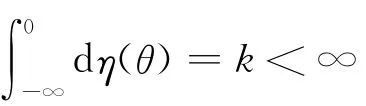
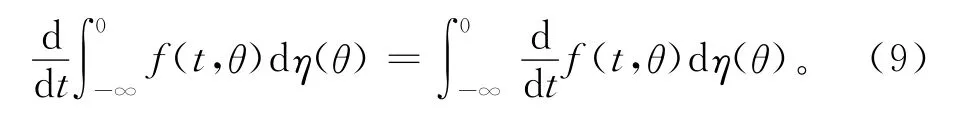
2 主要結果

定理1 假設下列條件成立：

（H1）：存在常數lj＞0，ξij＞0，i，j＝1，2，…，N，使得對任意x，y∈RN有：

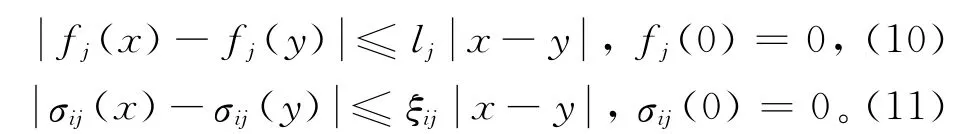
（H2）存在常數μ＞0，使得

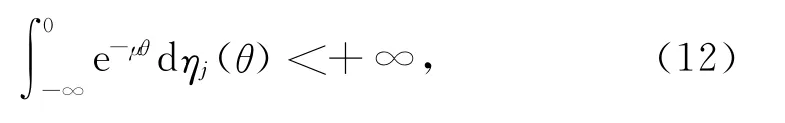
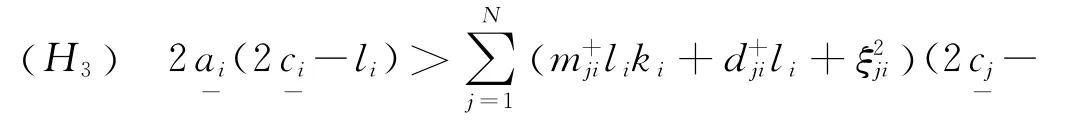
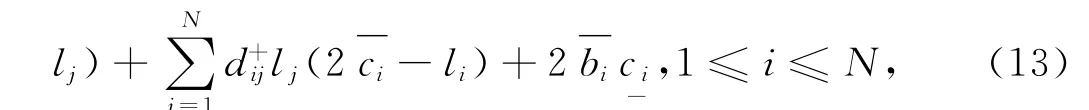
為證明方便，將系統（1）可化為：

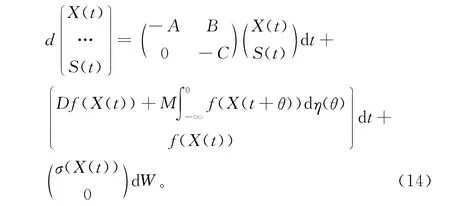
由條件（H1）可以證明系統（14）等式右端系數滿足Lipschitz條件，證明如下：

設

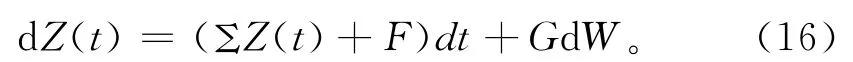
顯然，由條件（H1），（15）和（16）可得

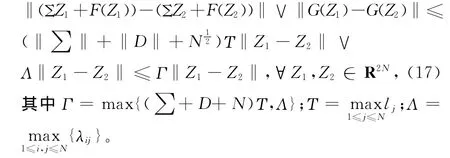
由（17）和引理1知系統（2）存在唯一滿足初值條件xi（θ）＝φi（θ），Si（θ）＝ψi（θ），i＝1，2，…，N，θ∈（－ ∞，0］解Z（t）＝（X（t），S（t））T，且以概率1連續。再證：平衡點z＊＝（0，0）T在均方意義下全局指數穩定。

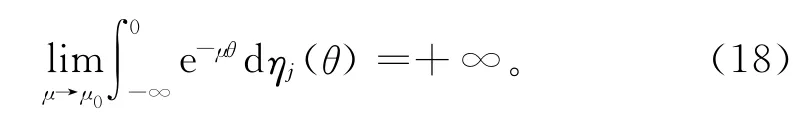
定義映射：

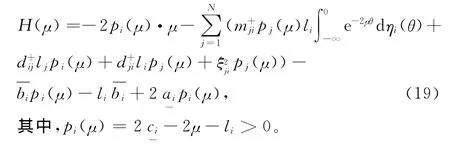
則由條件（H3）得：

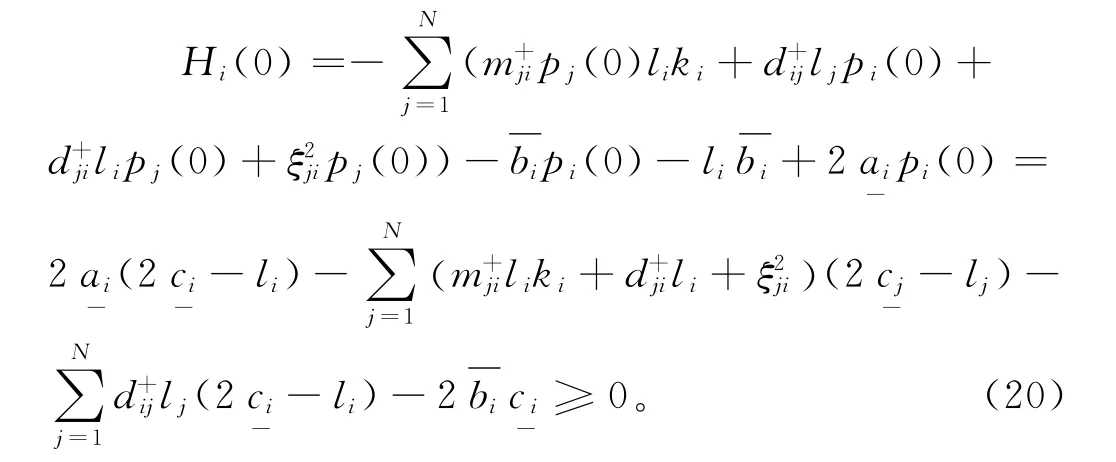
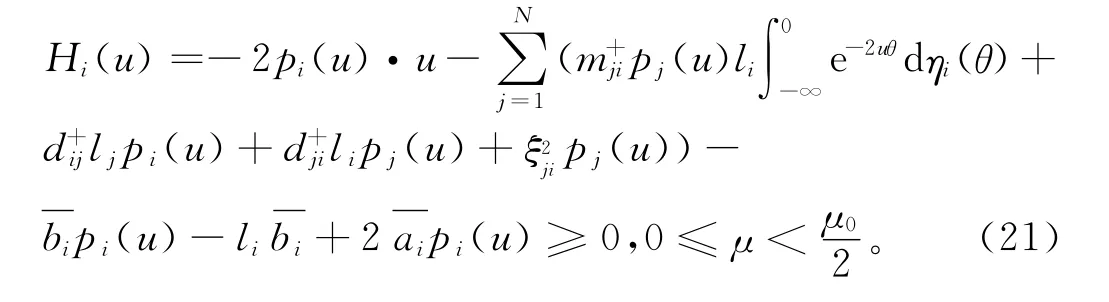
定義Lyapunov泛函

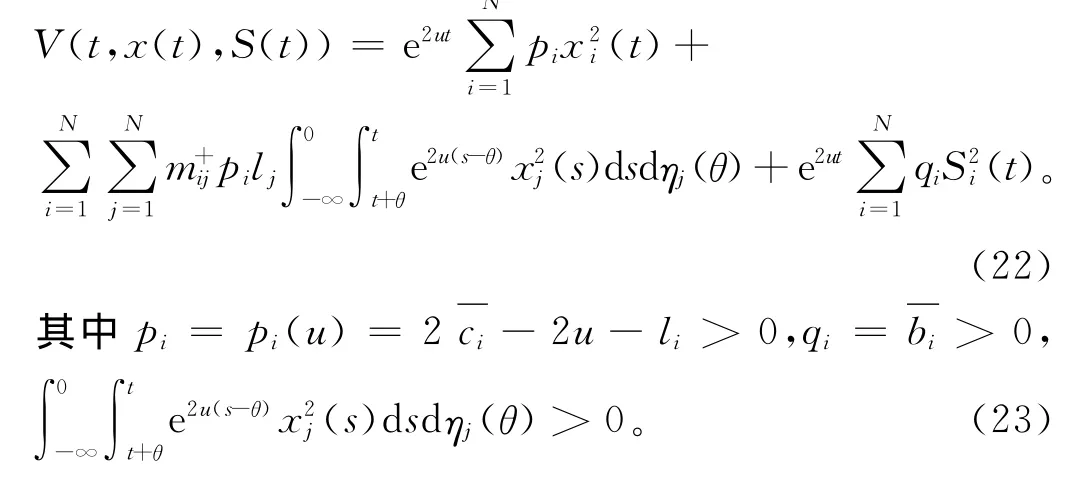
根據引理2得：

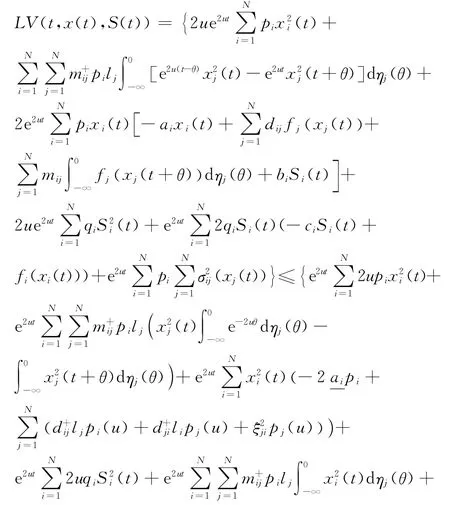
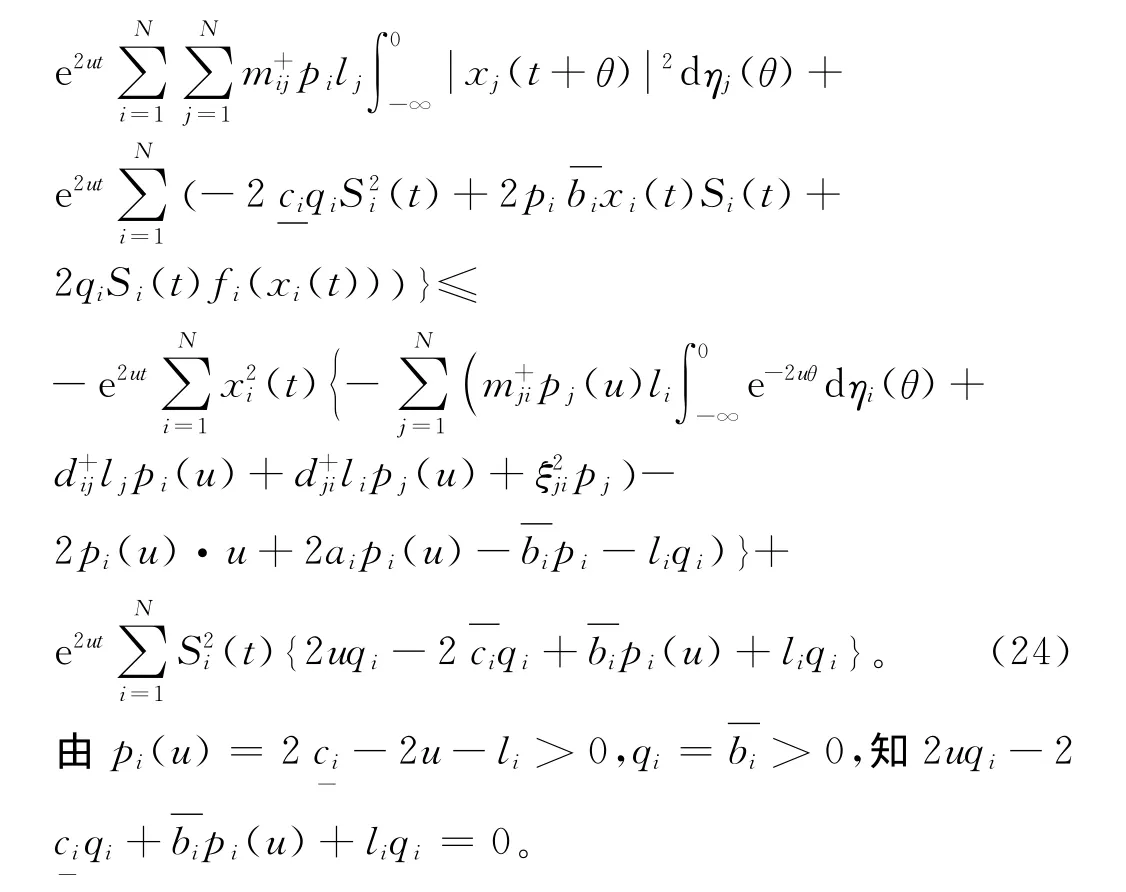
由H（u）≥0，得

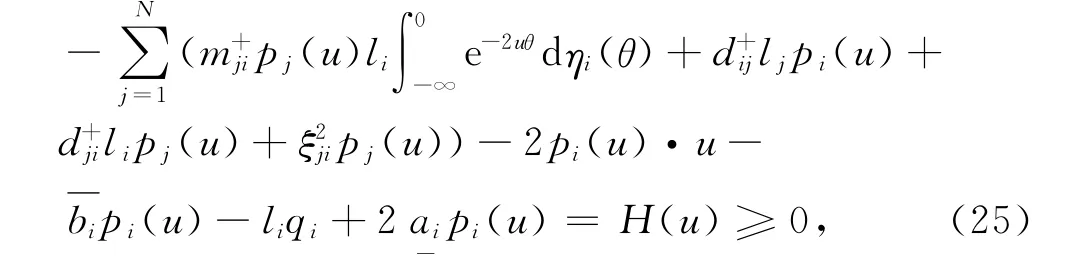
因此LV（t，x（t），S（t））≤0。

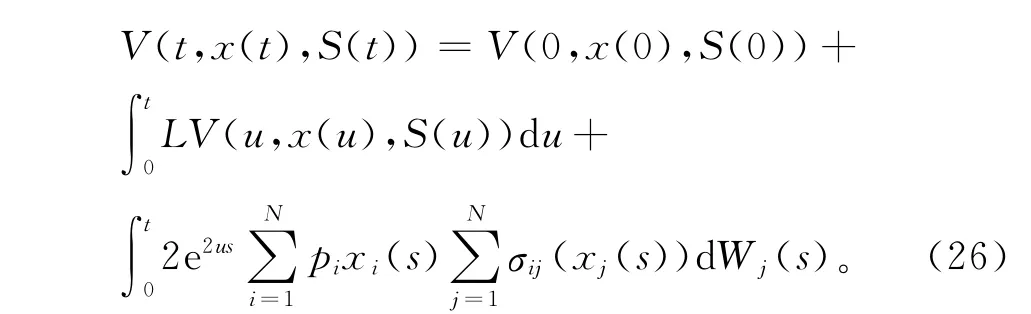
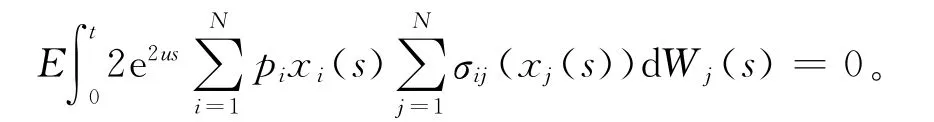
又因LV（t，x（t），S（t））≤0，所以有：

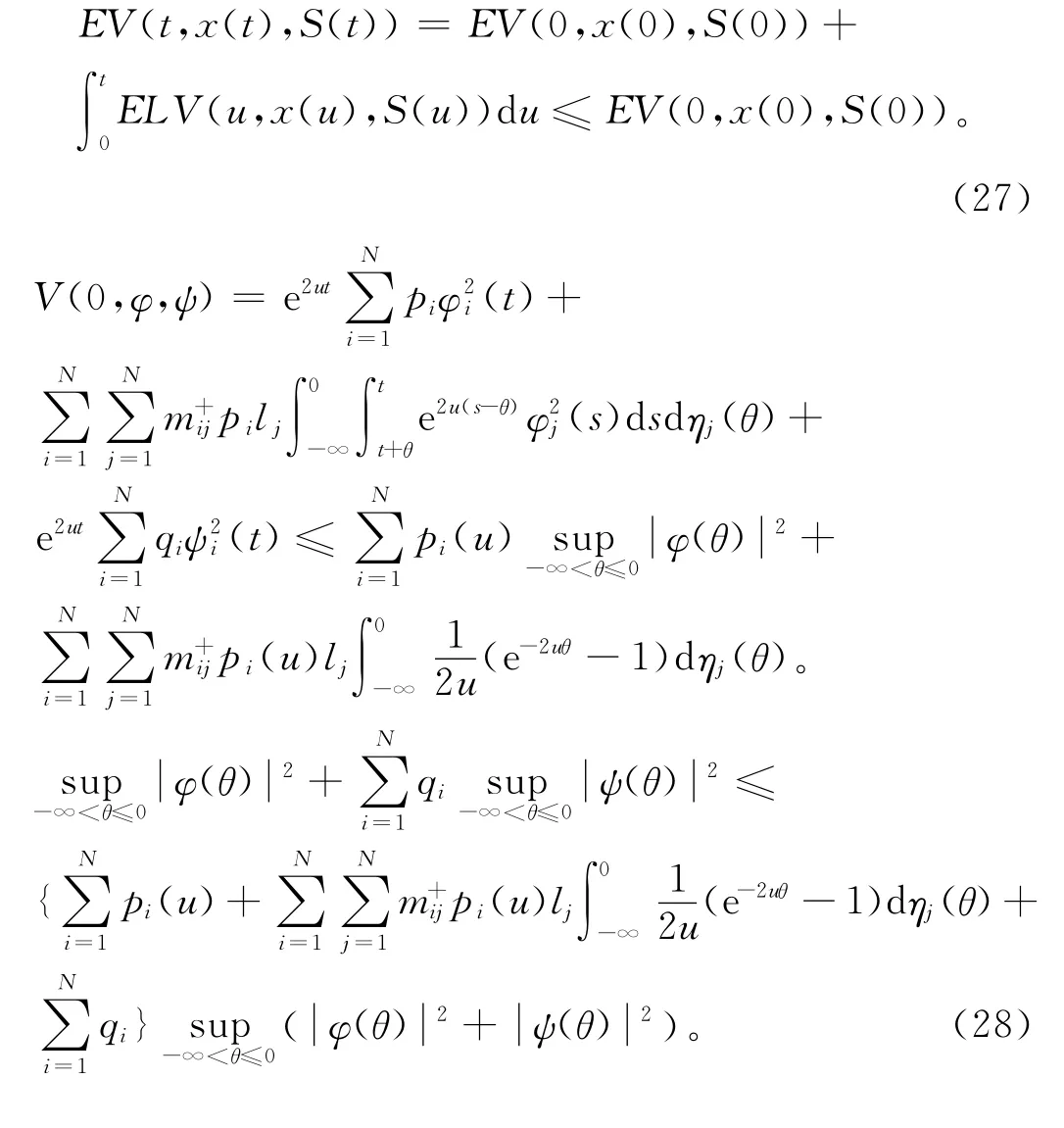
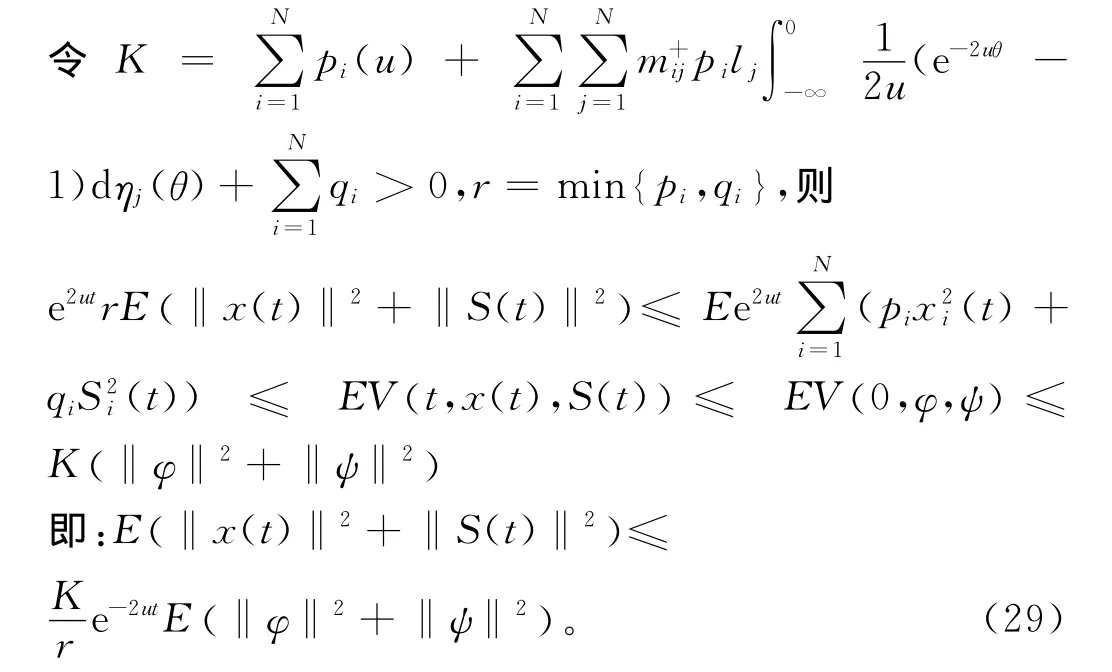
則根據定義3，系統（2）的平衡點z＊＝（0，0）T在均方意義下是全局指數穩定的，并且對每個A∈Al，B∈Bl，C∈Cl，D∈Dl，M∈Ml，系統（1）在均方意義下是全局指數魯棒穩定的，依據引理3，平衡點z＊＝（0，0）T也是幾乎必然指數一致穩定的。即網路幾乎必然指數穩定。注：由文獻［5］知，S-分布時滯的系統包含了離散時滯和分布時滯的系統，反之不成立。因此，文獻［2-4］研究的問題是本文研究問題的特例，本文推廣了這些文獻中的有關結果。另外，S-分布時滯還包含了無窮分布時滯［18］的情形。

3 仿真實驗

考慮如下S－分布時滯隨機競爭神經網絡（N＝2）：

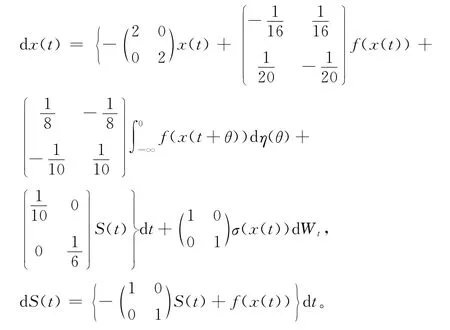
其 中fj（xj（t））＝sin（xj（t）），σij（xj）＝sin（xj（t）），ηj（t）＝，λj＞0，i，j＝1，2，

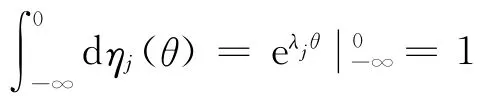
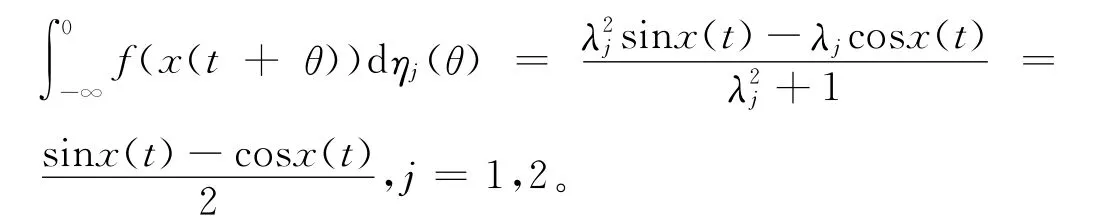
取pi＝1，i＝1，2，則滿足定理1中的條件，從而系統在均方意義下是全局指數穩定的。

取初值條件 （2，－1，－3，2） 得仿真圖像：

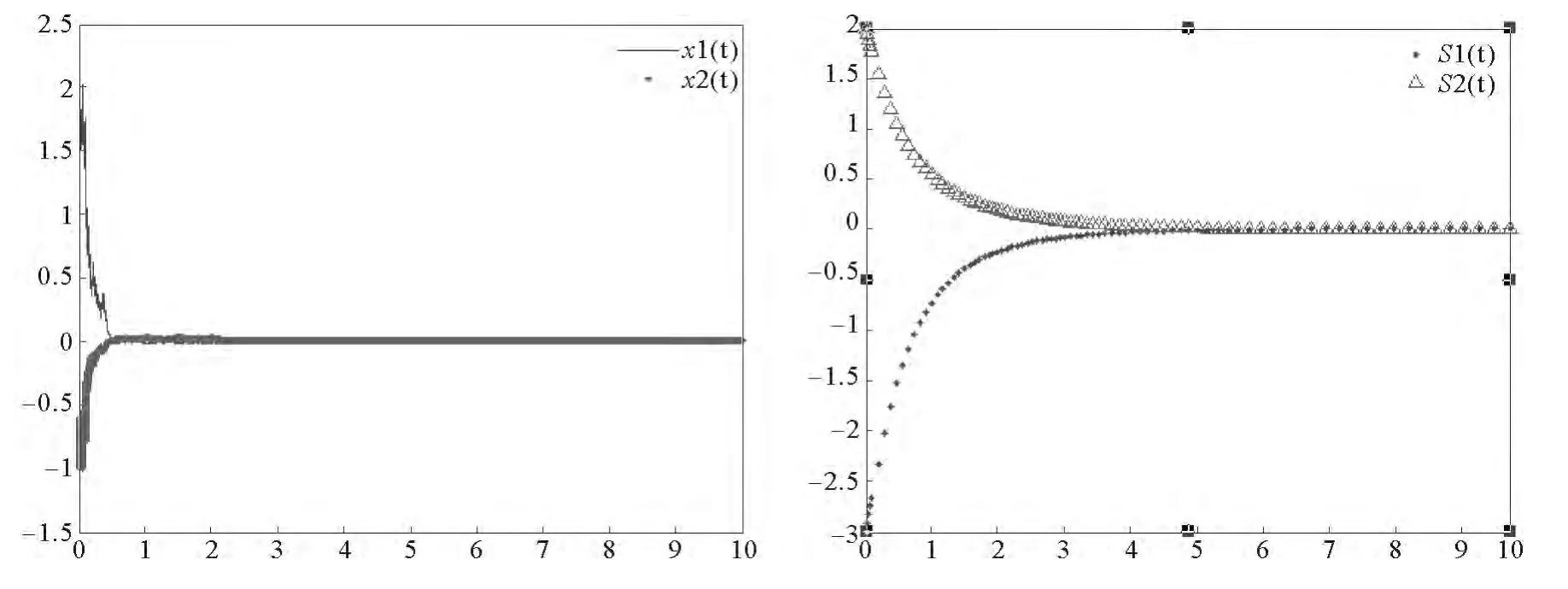
圖1 初值取 （2，－1，－3，2）T時系統的仿真結果Fig．1 The simulation results of the system at initial value （2，－1，－3，2）T

［1］Meyer-Baese A，Pilyugin S S，Chen Y.Global exponential stability of competitive neural networks with different time scale［J］.IEEE Transactions on Neural Networks，2003，14：716-719.

［2］Wei Xuerui.Exponential stability of competitive neural networks with different time-varying delays［J］.Journal of Biomathematics，2012，27（3）：455-462.

［3］Xiaobing Nie，Jinde Cao.Multistability of competitive neural networks with time-varying and distributed delays［J］.Nonlinear A-nalysis：Real World Applications，2009，26（3）：928-942.

［4］Kwon O，Lee S，Park J.Improved delay-dependent exponential stability for uncertain stochastic competitive neural networks with time-varying delays［J］.Phys Lett，2008（A374）：219-233.

［5］王林山.時滯遞歸神經網絡［M］.北京：科學出版社，2008：86-96.

［6］Wang L S，Xu D Y.Global asymptotic stability of bidirectional associative memory neural networks with s-type distributed delays［J］.International Journal of Systems Science，2002，33（11）：869-877.

［7］張偉偉，王林山.S－分布時滯隨機區間細胞神經網絡的全局指數魯棒穩定性［J］.山東大學學報，2012：47（3），87-92.

［8］Qintao Gan，Renxi Hu，Yuhua Liang.Adaptive synchronization for stochastic competitive neural networks with mixed time-varying delays［J］.Commun Nonlinear Sci Numer Simulat，2012，17：3708-3718.

［9］Haibo Gu，Haijun Jiang，Zhidong Teng.Existence and global ex-ponential stability of equilibrium of competitive neural networks with different time scale and multiple delays［J］.Journal of Franklin Institute，2010，347：719-731.

［10］Huabin Chen.New delay-dependent stability criteria for uncertain stochastic neural networks with discrete interval and distributed delays［J］.Neurocomputing，2012（101）：1-9.

［11］Ludwig Arnold.Stochastic Differential Equation Theory and Applications［M］.Hoboken：A wiley-interscience publication，1971：88-92.

［12］Xuerong Mao.Stochastic Differential Equation and Applications［M］.Berlin：Springer-verlag，1997：149-152.

［13］Ruojun Zhang，Linshan Wang.Global exponential robust of interval cellular neural networks with s-type distributed delays［J］.Mathematical and Computer Modelling，2009（50）：380-385.

［14］鄭祖庥.泛函微分方程［M］.合肥：安徽教育出版社，1994.

［15］鐘守銘，劉碧森，王曉梅，等.神經網絡穩定性理論［M］.北京：科學出版社，2008：208-301.

［16］Tolga Ensari，Sabri Arik.New results for robust stability of dynamical neural networks with discrete time delays［J］.Expert Systems with Applications，2010，37：5925-5930.

［17］Liao Wentong，Wang Linshan.Existence and global attractability of almost periodic solution for competitive neural networks with time-varying delays and different time scales［J］.Advances in Neural Networks，2006，3971：297-302.

［18］Bing Li，Daoyi Xu.Mean square asymptotic behavior of stochastic neural networks with infinitely distributed delays［J］.Neurocomputing，2009，72：3311-3317.