光伏發電量的預測綜述

張 玉，張振濤，莫 寒

ZHANG Yu, ZHANG Zhen-tao, MO Han

（桂林理工大學 廣西建筑新能源與節能重點實驗室，桂林 541004）

0 引言

面對全球日益嚴重的能源危機，人類加快了對新能源探索的腳步。太陽能作為目前全球最大的可再生能源，具有極高的利用價值。發電量預測是太陽能利用的一項非常重要的指標，對大電網的分配調度會產生一定的影響。然而光伏陣列的輸出特性受到光照強度、溫度、濕度等其他外界因素的影響，具有不確定性[1,2]，這使得光伏發電量的預測變得更加困難。

圖1 光伏發電量受環境因素影響示意圖

對于一個光伏發電系統，其發電量的預測對于大電網調度十分重要，我們需要掌握的是該系統在某一時刻的實時發電功率，在不同情況下選擇合理的預測方法對發電量預測能起到事半功倍的效果。目前光伏發電量的預測方法有很多種，按照時間尺度可以分為超短期預測、短期預測和中長期預測。按照研究過程可以分為直接預測和間接預測[3]。這些方法雖然可以將大多數的預測方法進行歸類，卻很難全面覆蓋，甚至有些預測方法的劃分界限十分模糊，不能系統的將光伏發電量預測的方法進行歸類。為此本文將光伏發電預測方法用數學統計預測法和人工智能預測進行分類，并在最后補充了一些其他的預測方法。實現了光伏發電量預測的完整化分類。

1 數學統計預測法

1.1 灰色理論預測法

所謂灰色理論預測法就是指利用灰色系統實現的預測模型。灰色系統的概念是在1982年由鄧聚龍教授首次提突出，他所描述的是介于部分信息已知的白色系統和部分信息未知的黑箱系統之間的過度系統。灰色系統可以通過對原始數的分析整理找出它們之間存在的聯系從而預測數據的變化規律從而達到預測的效果。GM(1,1)模型是灰色系統中較為常用的動態預測模型，該模型的構成只有一個單一變量的一階微分方程，預測過程大致可以分為累加—擬合—累減三個步驟[4]。

文獻[5,6]分別采用GM(1,1)模型對光伏發電量進行預測，單一的采用GM(1,1)模型對光伏的發電量雖然可以起到預測的效果，但其預測結果與實際結果存在一定的偏差，為了能夠得到較為準確的預測結果，采用GM(1,1)殘差修正模型對原有的預測模型進行修正。將一天中各個時間段的發電量構成一個時間序列，以一天中光照強度最強發電量最大時為分界點，把一天中的預測分為兩個階段分別進行預測。結果顯示，基于殘差修正的GM(1,1)模型效果更好，其預測結果更為接近實際值。

1.2 多元線性回歸預測法

在生活中一種現象的發生往往與多個因素存在相互關聯，此時就需要多個相關因素作為自變量解釋因變量的變化規律，這種模型就是多元線性回歸模型。在光伏發電量預測中，光伏系統的發電量受到輻射強度和溫度等因素的影響，因此可以以這些因素作為光伏發電系統的多元線性回歸模型的輸入。

文獻[7]將由18塊京瓷KC130GH-2P多晶硅太陽能電池組件串聯的光伏陣列作為研究對象，對該系統的輻射強度、環境溫度、組件背板溫度、風速、發電功率以及每小時發電量6個自變量建立多元線性回歸模型，并采用F檢測法對回歸方程顯著性檢測后說明該模型有很好的擬合效果。將對預測結果在不同的天氣情況下進行分類，在晴天，多云，陰轉天三種情況下與將預測值與實際值比較后發現，在晴天的預測值較實際值偏高，陰轉云的情況下預測值較實際值偏低，多云天氣的預測值則有較好的預測效果。

1.3 時間序列預測法

時間序列預測法是一種以時間為序列，根據歷史數據揭示事物發展規律的數學統計方法。在光伏發電量預測技術中將光伏系統某一時段內的發電量看作一個隨時間周期變化的隨機數列。通過曲線擬合和參數評估來建立預測系統的數學模型，自回歸—滑動平均模型（ARMA）是時間序列預測法中較為常見的預測模型。文獻[8]中作者建立了ARMA模型在光照充分的晴天下對光伏系統的短期發電量進行預測，結果表明，ARMA模型在晴天中有較高的預測精度。

數學統計預測法雖然在光伏發電量預測中可以實現預測的效果，其預測結果雖然和歷史數據存在著某種相互聯系，但這種聯系并不能起到決定性的作用。在短期預測中光伏發電量受環境因素影響時效性較強，這種特性導致此類方法一旦受到環境因素變化較大情況時，預測結果變化緩慢，預測精度較低等情況。但這種方法易于實現，正是由于與歷史數據存在著相互聯系使得在中長期發電量變化趨勢上有一定的可取性。

2 人工智能預測法

2.1 BP神經網絡預測法

BP神經網絡是一種按照誤差逆向傳播算法訓練的多層前饋網絡，是由大量的神經元相互連接而成的非線性動態系統，使用最速下降法通過反饋結果進而不斷調整網絡的權值和閘值，使網絡的輸出達到最優化。BP神經網絡模型包括輸入層，隱含層和輸出層三個部分。目前，通過BP神經網絡與其他算法相結合可延伸出多種預測方法，如基于牛頓法小波神經網絡預測模型，基于遺傳算法神經網絡預測模型，基于BP神經網絡—馬爾科夫鏈預測模型，基于粒子群BP神經網絡預測模型等。

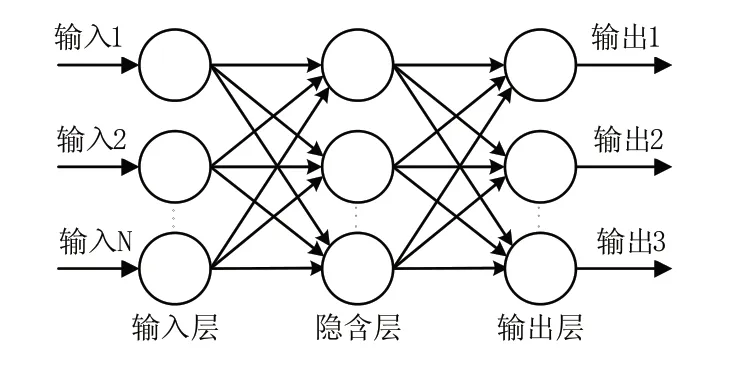
圖2 BP神經網絡結構示意圖

2.1.1 基于牛頓法小波神經網絡預測模型

文獻[9]描述了一種基于牛頓法小波神經網絡的光伏發電預測模型，在原有神經網絡的預測模型中做了以下兩點改進，其一在訓練方法上選擇能夠較好地處理復雜問題的擬牛頓算法；其二是在神經網絡的結構上采用能夠較好處理小信號的小波神經網絡進行改進。通過仿真結果分析發現，該模型比普通的神經網絡預測模型預測精度更高，尤其針對不同季節采用該模型有較好的預測效果。

2.1.2 基于遺傳算法神經網絡預測模型

文獻[10]描述了一種改進的神經網絡算法，在神經網絡的基礎上加入遺傳算法，建立GA-BP預測模型。首先對環境溫度、風速、濕度、輻射強度等環境因素進行主成分分析，剔除掉無用信息并篩選出主要成分作為GA-BP預測模型的輸入。設定初始種群數，經過遺傳迭代，得到BP神經網絡的最優權值和閘值，經過BP神經網絡訓練后得到最終預測結果。對預測結果分析后表明主成分分析的遺傳優化神經網絡預測模型比一般的BP神經網絡預測模型在預測結果上更為準確。

2.1.3 基于BP神經網絡—馬爾科夫鏈預測模型

文獻[11]中提到一種基于BP神經網絡—馬爾科夫鏈的光伏發電預測方法，將前一日的發電量及最高和最低溫度以及預測日當天的最低和最高溫度作為模型的輸入，在經過BP神經網絡預測后根據預測的相對誤差采用馬爾科夫鏈模型進行修正。避免了在建模的過程中忽略了實際的光照數據等。結果表明該模型具有較高的預測精度。

2.1.4 基于粒子群BP神經網絡預測模型

文獻[12]中描述了一種基于粒子群的BP神經網絡(PSO-BP)光伏發電預測模型，該模型將神經網絡中需要調整的權值和閘值映射為PSO中的粒子，通過粒子間的競爭與合作不斷優化這些參數，使網絡的訓練效率大大提高。通過與普通BP神經網絡的預測結果相比較，基于PSO-BP神經網絡的光伏發電預測模型有更好的預測效果。

2.2 支持向量機預測法

支持向量機（SVM）是1995年由Corinna Cortes和Vapnik提出的，是一種基于統計學習理論的模式識別方法，在解決一些復雜的非線性系統中具有極好的效果。其主要思想可以概括為將一個樣本空間映射到一個高維空間中，在原有樣本空間中線性不可分的問題在高維空間中實現線性可分。

2.2.1 基于魯棒學習最小二乘支持向量機預測模型

文獻[13]中提到了一種改進后的基于魯棒學習最小二乘支持向量機（RLS-SVM）的光伏預測模型。在傳統的LS-SVM基礎上采用魯棒學習提高系統的魯棒性，同時減少了系統的“過擬合”現象。該模型以歷史發電量，太陽輻射強度和環境溫度作為輸入，以光伏發電功率為輸出，與LS-SVM模型及RBF神經網絡做了仿真對比。研究結果表明，RLS-SVM光伏預測模型有更高的預測精度，能夠準確的預測出光伏陣列額定輸出功率，有效地解決了光伏發電的隨機化問題。

2.2.2 基于相似日和最小二乘支持向量機預測模型

文獻[14]提出了一種基于相似日和最小二乘支持向量機的光伏發電預測模型，該模型首先將天氣因素歸類為晴天、陰天和雨天。將溫度和濕度作為兩個主要參考量，計算出預測當日與歷史數據的相似度，根據相似度選擇相應的相似日，由相似日的光伏發電量和預測日當天的氣候特征來預測這一天的發電量。這種模型在一定程度上減小了天氣變化對預測值的影響，相比于SVM模型有更好的預測效果。

人工智能預測法有預測精度高、響應速度快等優點，BP神經網絡和支持向量機預測法是目前較為常用的人工智能預測法，許多其他的智能預測模型也都是基于這兩者加入其他算法進行改進。而這也使原本復雜的系統實現起來更為困難，尤其BP神經網絡需要大量的原始數據進行訓練。而支持向量機面對大規模的訓練樣本時更是難以實施。這些預測方法理論性較強，只能借助計算機實現仿真分析，很難與大型光伏發電站的實際情況相結合。

3 其他預測方法

在研究光伏陣列的數學模型中，我們不難發現影響光伏發電量的主要因素是溫度和輻射強度[1,3]。針對這一特性，人們提出另外一種間接預測光伏發電量的方法，即建立瞬時太陽輻射模型，例如Hottel輻射預測模型或者Liu-Jordan輻射模型[15]等。這種預測方法以天文輻射作為輸入變量，以地表接收到的太陽輻射為輸出建立數學模型來間接預測實時的光伏發電量。同樣利用此方法建立逐時太陽能預測模型和日總太陽能預測模型，可以實現以日為單位的光伏發電量。但這種方法實施起來十分困難，目前國內外對這方面的研究尚處在起步階段。

從光伏電池板的電路特性出發可以直接采用日本工業標準（JIS）進行光伏發電量的預測，這種方法較為簡單，通過光伏陣列的I/V特性曲線由數學公式計算出其輸出功率。與之相似的三維模擬計算法則是尋找輸出的瞬時最大功率，計算出瞬間的發電量并將其累加起來進而算出一天的發電量乃至一月的發電量。該方法充分考慮了影響光伏發電量的各個因素，包括太陽高度角的選擇及配線方案等[16]。但這些方法僅在理論上存在可行性，實際實施起來具有一定的困難。

4 我國光伏發電量預測的發展現狀

目前我國正在走可持續發展的道路并且大力推進“生態文明”建設，對能源的要求向著清潔環保的方向發展。在這樣的時代背景下我國的光伏發電產業得到了迅猛的發展。

根據德國商報報道，2014年最新全球十大光伏供應商排名中中國企業就有四個之多，常州天合光能有限公司更是首次成為全球最大的光伏供應商。其他三家分別為中國英利能源有限公司、無錫尚德太陽能有限公司和晶科能源有限公司。在新增裝機容量方面，根據國家可再生能源中心統計數據顯示，由2008年以前的零增長發展到2012年的新增裝機容量達328MW，僅次于德國和意大利，位列世界第三。這一趨還在以更快的速度增長。到2020年前后累計裝機總量可達20000GW。國家電網公司《關于做好分布式光伏發電并網服務的工作的意見》中規定，自2012年11月1日起不超過6MW的光伏發電項目可以到當地的電網公司申請免費并網運行[1,3]。這一政策的頒布也促使了國內的光伏產業的快速發展。

在光伏發電量預測方面，我國華北電力大學栗然等結合當地氣候特征模擬了30MW光伏電站發電量數據，利用支持向量機和回歸分析法做了發電量的預測。但該方法僅模擬光伏發電站的預測數據，沒有實驗數據作為參考。華中科技大學在對18kW光伏發電站的研究中對每5分鐘系統的發電量進行采集，陳昌松等結合這些數據和大量氣象數據建立了基于相似日的神經網絡預測模型。取得了很好的預測效果，但也同樣存在著一旦環境急劇變化預測失真等情況[17]。

而在德國光伏發電量的預測已不僅僅在理論預測階段，2009年就有6000MW光伏發電量在德國電網運行，RWE運輸風暴公司（RWE TSO）與一些科研院在光伏發電量預測的準確性上做了深入研究，他們不僅能夠準確的對光伏的發電量進行預測，更重要的是他們已經在考慮系統的平衡性、網絡損耗、擁堵、儲能等問題[18]。

總的來說，雖然我國的光伏發電量在以迅猛的速度發展，但由于我國的光伏產業起步較晚，也存在著很多因素制約著其發展，使得我國的光伏產業與國外的發達國家存在著一定差距。

5 光伏發電量預測的發展方向

隨著光伏產業的大力發展，光伏發電量預測技術也日漸成熟。但是目前的研究方法過分依賴大量的原始數據及智能算法，而忽略了光伏陣列的電氣特性以及影響光伏陣列輸出功率的外在因素，因此，我們的預測工作仍有許多需要改進的地方。

光伏產業的飛速發展必將帶來更多大規模的光伏發電站與大電網的并網，光伏并網后其輸出功率的工程模型如式(1)：

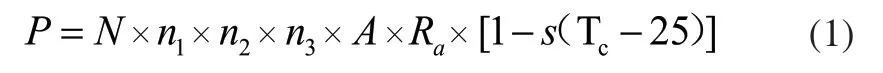
式(1)中P為光伏陣列的輸出功率，N為光伏組建個數，n1為光伏轉換效率，n2為最大功率點跟蹤工作效率，n3為逆變器效率，A為光伏組件的面積，a為光伏陣列傾角，Ra為光伏陣列所受福照度，s為溫度系數，Tc為光伏組件背板溫度[6]。由此可見不僅溫度和輻射強度對光伏發電量有影響，光伏陣列的安裝角度等同樣對光伏發電量存在一定的影響。由于目前光伏陣列的安裝角度較為固定，尤其大型光伏發電站一旦安裝很難更改。以往，光伏板的最佳安裝角度都是根據太陽高度角來進行設置，而我國地理環境復雜，一些地區具有獨特的氣候特征，僅僅通過太陽高度角確定下來的安裝角度不一定是最優的，因此，在安裝角度上，我們可以綜合考慮太陽高度角以及當地特有的氣候特征，確定當地的最佳安裝角度。

6 結束語

在對目前現有的大量有關光伏發電量預測的文獻調研后，本文系統的將光伏發電量預測的方法歸為數學統計預測法和人工智能預測法兩大類。并相應地補充了其他有關光伏發電量預測的方法，起到了查漏補缺的效果，同時分析了各自的優缺點。數學統計法可以大致模擬出預測數據的變化趨勢，但其過分依賴歷史數據，存在預測結果滯后等特點。人工智能算法有很好的預測精度，也有很快的響應速度，但其理論性較強，多數情況下在計算機上進行建模與仿真，很難與大型光伏發電站的實際情況相結合。通過建立太陽能輻射模型的間接預測以及單純的考慮光伏陣列的I/V特性預測同樣存在實現起來過于復雜和考慮過于片面的缺點。未來光伏發電量預測技術應先在有的基礎上加以改進完善，兼顧考慮環境因素、電氣特性以及最佳安裝角度等問題，實現預測精度更高、響應速度更快、考慮更為全面等特點。

[1]王磊.光伏發電系統輸出功率短期預測技術研究[D].合肥工業大學,2012.

[2]Il-Song Kim,Myung-Bok Kim,Myung-Joong Youn.New Maximum Power Point Tracker Using Sliding-Mode Observer for Estimation of Solar Array Current in the Grid-ConnectedPhotovoltaic System[J].IEEE Transaction Industrial Electronice,2006,53(4):1027-1035.

[3]袁曉玲,施俊華,徐杰彥.計及天氣類型指數的光伏發電短期出力預測[J].中國電機工程學報,2013,34:57-64,12.

[4]姜強鑫.基于小波神經網絡的分布式光伏發電出力預測[D].南昌大學,2012.

[5]徐靜,陳正洪,唐俊,李芬.建筑光伏并網發電系統的發電量預測初探[J].電力系統保護與控制,2012,18:81-85.

[6]李光明,廖華,李景天,趙恒利,黃波,何京鴻.并網光伏發電系統發電量預測方法的探討[J].云南師范大學學報(自然科學版),2011,02:33-38,64.

[7]李光明,劉祖明,何京鴻,趙恒利,張樹明.基于多元線性回歸模型的并網光伏發電系統發電量預測研究[J].現代電力,2011,02:43-48.

[8]蘭華,廖志民,趙陽.基于ARMA模型的光伏電站出力預測[J].電測與儀表,2011,02:31-35.

[9]楊超穎,王金浩,王碩,徐永海,黃浩.基于擬牛頓法小波神經網絡的光伏發電系統短期功率預測模型[J].中國電力,2014,06:117-124.

[10]袁曉玲,施俊華,徐杰彥.基于BP神經網絡的光伏發電短期出力預測[J].可再生能源,2013,07:11-16.

[11]姜僑娜,陳中.BP-馬爾科夫組合預測方法在光伏發電量預測中的應用[J].電力需求側管理,2011,06:21-24.

[12]張佳偉,張自嘉.基于PSO-BP神經網絡的短期光伏系統發電預測[J].可再生能源,2012,08:28-32.

[13]李洪珠,賈威,聶苓,鄂小雪.基于魯棒LS-SVM在光伏發電預測中的應用[J].計算機測量與控制,2013,05:1166-1167,1170.

[14]傅美平,馬紅偉,毛建容.基于相似日和最小二乘支持向量機的光伏發電短期預測[J].電力系統保護與控制,2012,16:65-69.

[15]Md Habibur Rahman,Susumu Yamashiro.Novel distributed power generating system of PV-ECASS using solar energy estimation[J].IEEE Transactions on Energy Conversion,2007,22(2):358-367.

[16]楊超,榑沼,弘貴.太陽能光伏發電系統發電量的預測方法[J].智能建筑電氣技術,2011,02:29-34.

[17]李芬,陳正洪,成馳,段善旭.太陽能光伏發電量預報方法的發展[J].氣候變化研究進展.2011,02:136-142

[18]Ernst B,Reyer,F,Vanzetta,J.Wind power and photovoltaic prediction tools for balancing and grid operation[J].2009 CIGRE/IEEE PES Joint Symposium.2009:1-9.