廈漳大橋索梁錨固結構承載力試驗研究
■張 帆,熊健民,周金枝 ■.湖北大學,湖北 武漢 430068;.湖北工業大學土木工程與建筑學院,湖北 武漢 430068
1 概述
廈漳跨海大橋北汊為主跨780m 的五跨連續半漂浮體系雙塔雙索面斜拉橋,跨度布置為(95 +230 +780 +230 +95)m,南汊主橋為雙塔雙索面半漂浮體系組合梁斜拉橋,跨度布置為(135 +300 +135)m;該橋起于廈門馬青路院前處,止于漳州龍海市后宅處。大橋工程主要包括北汊北引橋、北汊主橋、北汊南引橋、海門島立交及收費服務區、南汊橋、海平互通立交組成。
南、北汊主橋索梁錨固形式均采用錨拉板式錨固結構,這種索梁錨固方式傳力路徑明確,構造簡單,施工、檢查和維修方便[1],但局部應力明顯集中,一些關鍵構造細節的疲勞可靠性不明確。為驗證結構設計正確性與制作工藝的合理性,確保結構的安全可靠,對南汊主橋索梁錨固結構進行1:1 足尺模型試驗。
通過對南汊主橋的整橋有限元計算,南汊主橋受力最大的錨拉板為Z12,綜合考慮錨固結構的承載能力與疲勞性能,選擇參照南汊主橋Z12 錨拉板制作本試驗模型。該試驗模型是1:1 足尺模型,高為6.1m,寬為2.39m。試驗模型制作廠家與實橋生產廠家是同一個廠家,保證了模型的整個制作和焊接工藝要求與實橋完全一致,材料也與實橋相同,為Q235 鋼。
廈漳跨海大橋斜拉索與主梁之間采用錨拉板式的錨固方式,如圖1所示,斜拉索在索塔上錨固采用鋼錨梁結構形式。
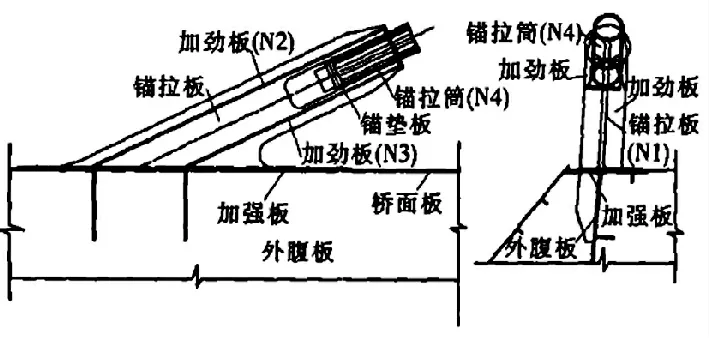
圖1 錨拉板式的錨固方式
2 有限元分析
2.1 材料參數
從錨固區的線彈性有限元分析結果可知,在成橋索力作用下,錨固結構錨拉板、錨管Von -Mises 應力值最大,某些區域的Von -Mises 應力值將達到材料的屈服強度,為了進一步研究錨固結構的極限承載力,需對索梁錨固結構進行了彈塑性分析[2]。計算中忽略結構初始缺陷,不考慮由于板件焊接引起的收縮變形。單元選用四節點三維殼單元SHELL181,鋼材采用雙線性等向強化材料模式,彈性模量E=2.1 ×105MPa,泊松比μ=0.3,初始屈服應力σy=360 MPa;考慮1%強化,切線模量Et=2.1 ×103MPa,采用Von-Mises 屈服準則。材料本構關系如圖2。
2.2 錨固結構承載能力分析
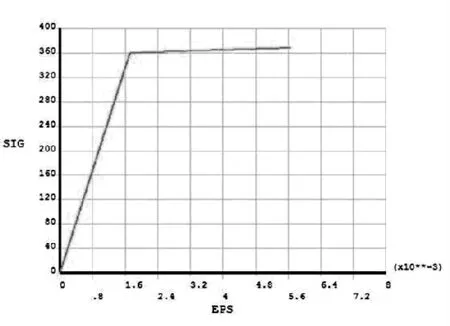
圖2 材料本構關系曲線
根據計算資料,Z12 斜拉索設計索力為5547.1kN,分別計算1.1倍、1.6 倍、2.1 倍、2.6 倍及3.1 倍最大索力下Von-Mises 應力值及塑性區間的發展趨勢。Z12 錨固結構錨拉板與錨管在各級荷載作用下的最大Von-Mises 應力值如表1、表2。錨拉板與錨管的塑性區間發展趨勢如圖4、圖5。
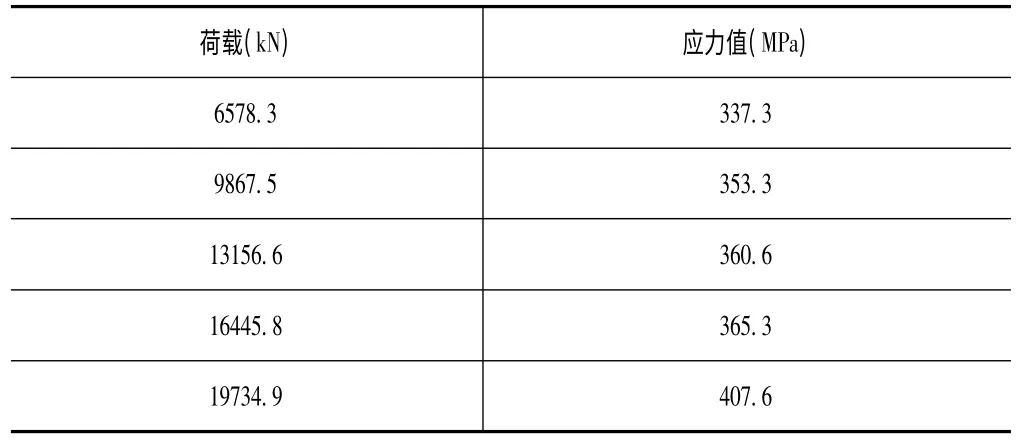
表1 各級荷載作用下錨拉板最大Von-Mises 應力值
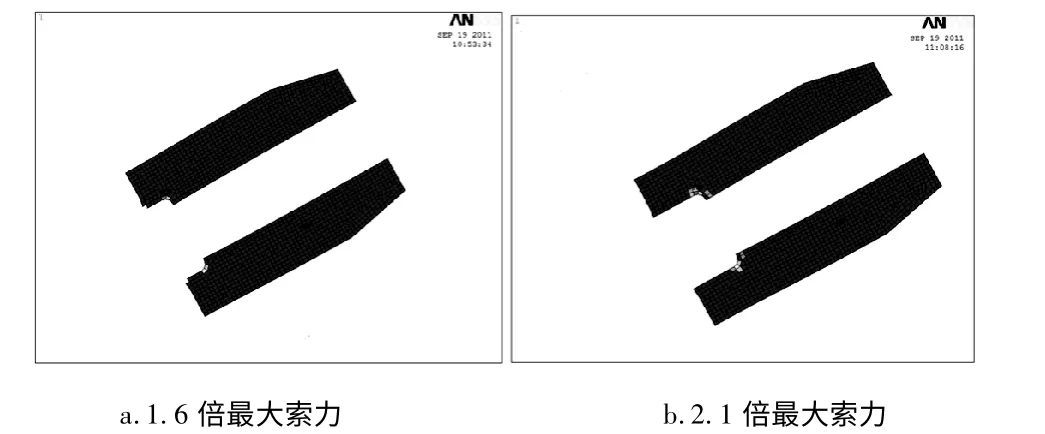
圖3 可以看出:隨著荷載的增加,錨拉板的圓倒角在處塑性區間不斷增大,當荷載增在最大索力的3.1 倍時,錨拉板與錨管連接處的圓倒角處已全部屈服。
圖4 說明了:隨著荷載的增加,在與錨拉板連接處的錨管處塑性區間不斷增大,當荷載增在最大索力的3.1 倍時,錨管全截面屈服。
2.3 錨固結構整體剛度分析
錨固結構在各級荷載作用下的最大位移如表3,將表3 的數據繪制成圖5。

圖3 錨拉板塑性區發展趨勢

圖4 錨管塑性區發展趨勢
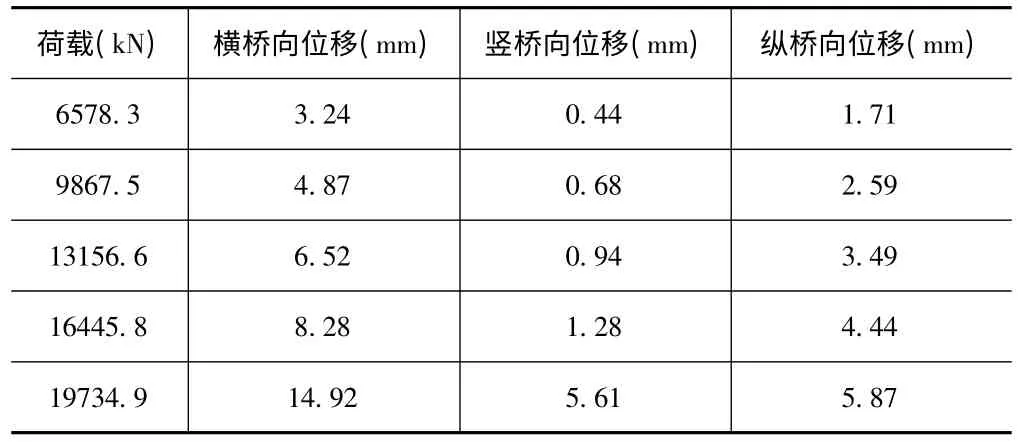
表3 各級荷載作用下錨固結構的最大位移值
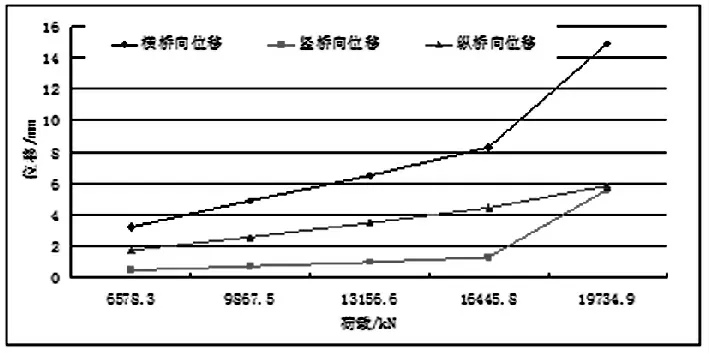
圖5 各級荷載作用下錨固結構的最大位移值
隨得荷載的增大,錨固結構的最大位移逐漸增大,在破壞荷載之前,錨固結構的最大位移與荷載幾乎成線性關系,在3.1 倍索力作用下,錨固結構的橫橋向與豎橋向的最大位移增長迅速,分別達14.92mm、5.61mm。
2.4 錨固結構局部穩定分析
根據計算參數,可得到錨管外徑與壁厚之比:
錨管外徑/壁厚之比=426/38=11.2 <100(235/fy)
根據《鋼結構計設規范》(GB 50017 -2003)規定“圓管截面的受壓構件,其外徑與壁厚之比不應超過100(235/fy)”[3]。可見錨管結構局部穩定性滿足規范要求。
3 試驗研究
3.1 試驗方法
由于承載能力試驗最大加載索力為Z12 拉索的最大索力的1.7 倍(10703kN),該荷載值已經遠大于MTS6000 試驗機的最大加載能力,因此,必需制作專門反力架進行加載,試驗采用2 個1300T 千斤頂利用自平衡方式進行,加載方式見圖6。

圖6 承載能力試驗加載圖
為防止意外事故發生,試驗采取分級加載,逐級增加,分級數為7級,達到最大荷載后一次卸載的加載方式,具體分級如下:0kN →2518kN→5037kN→6296kN→8814kN→10074kN→10703kN→0kN。每級荷載持荷1 分鐘后,進行應變測試讀數,讀數完成后,進行下一級加載。卸載到0kN 后,等待5 分鐘后再讀數。
3.2 試驗結果
根據對錨固結構主要受力構件在1 倍索力作用下各測點的Von -Mises 應力實測值的測算,1 倍設計索力作用下,錨拉板開口兩側受力基本對稱,錨固結構的最大的Von -Mises 應力值為336.8MPa,出現在錨拉板與錨管連接圓弧處,其他區域絕大部分測點Von -Mises 應力值在80MPa 以內。
對錨固結構主要受力構件在1.7 倍設計索力作用下各測點的Von-Mises 應力實測值的測算。可以看出,1.7 倍設計索力作用下,錨拉板開口兩側受力基本對稱,錨固結構的最大的Von -Mises 應力值為361.6MPa,出現在錨拉板與錨管連接圓弧處,已超過其屈服應力360MPa,其他區域絕大部分測點Von-Mises 應力值在100MPa 以內。
圖7 為錨拉板與錨管連接圓弧附近測點在各級荷載作用下的Von-Mises 應力。從圖7 可以看出,0.8 倍設計索力前,Von-Mises 應力與荷載呈線性關系;當荷載加載到設計索力的1.4 時,圓弧處的8 號測點與16 測點Von-Mises 應力值分別達到360.5MPa、360.1MPa,已達到材料的屈服應力。
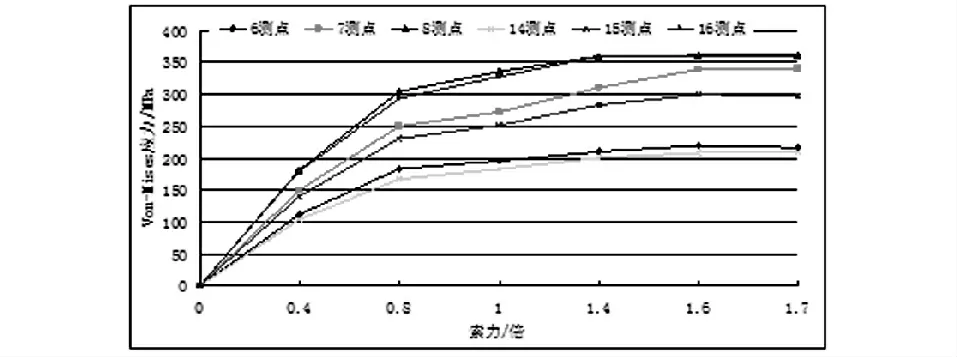
圖7 錨拉板部分測點在各級荷載作用下的Von-Mises 應力實測值
4 結論
(1)錨固結構的最大位移隨得荷載的增加而增大,在破壞之前,錨固結構的最大位移與荷載幾乎成線性關系,在3.1 倍索力作用下,錨固結構的橫橋向與豎橋向的最大位移增長迅速,分別達14.92mm、5.61mm;
(2)錨固結構在1.6 倍索力作用下,局部區域開始屈服,最大的Von-Mises 應力值為361.2MPa,出現于錨管與錨拉板連接圓弧附近[4];隨著荷載的增大,錨拉板的塑性區間沿焊縫不斷增高,當荷載增大加2.1 倍索力時,錨拉板與錨管連接圓弧處屈服面積達6000mm2,錨管屈服面積達整個截面的1/4;當荷載達3.1 倍索力時,錨管全截面屈服。
承載能力試驗結論:(1)各級荷載作用下,錨拉板開口左右兩側受力基本對稱,整體應力水平不高;(2)錨固結構應力隨荷載的增加而增大,當荷載加載到索力的1.4 時,錨拉板圓弧處的8 號測點與16 測點Von -Mises 應力值分別達到360.5MPa、360.1MPa,已達到材料的屈服應力;1.7 倍索力作用下,除錨拉板與錨管連接圓弧處測點的Von-Mises 應力值為361.6MPa,其他區域測點Von-Mises 應力值均在100MPa 以內;(3)結構試驗后進行檢查表明,沒有任何裂紋出現,錨固構造十字接頭處抗層狀撕裂能力滿足要求。
綜上所述,南汊主橋錨固結構具有足夠的承載能力,能夠保證運營的安全性。
[1]嚴國敏.現代斜拉橋.成都:西南交通大學出版社,1996.
[2]林元培.斜拉橋.北京:人民交通出版社,1998.
[3]李富文等.鋼橋.北京:中國鐵道出版社,1992.
[4]李本偉.斜拉橋索梁錨固區模型試驗與計算分析.西南交通大學研究生學位論文,1996,5.

