用于微振動控制的隔振器分析和實驗

馬俊

（四三一廠軍代表室，遼寧 葫蘆島 125004）

用于微振動控制的隔振器分析和實驗

馬俊

（四三一廠軍代表室，遼寧 葫蘆島 125004）

首先從隔振系統(tǒng)頻響函數(shù)出發(fā)，得到系統(tǒng)最優(yōu)頻響表達式，然后根據(jù)最優(yōu)頻響條件，設(shè)計了一種用于微振動控制的隔振器，并通過實驗測試隔振器的特性，獲得了由隔振器和不同質(zhì)量元件構(gòu)成的系統(tǒng)的振動加速度和振動傳遞率。實驗與理論計算結(jié)果一致性較好，說明設(shè)計是正確的。

振動與波；隔振器；微振動；最優(yōu)頻響；波紋管

微振動是影響高精度遙感衛(wèi)星指向精度和成像質(zhì)量等關(guān)鍵性能的主要因素，由于其微小性、固有性、寬頻性和難控性，航天器的微振動力學環(huán)境極為復雜和特殊，分析與控制難度都很大。在實際中，兩參數(shù)隔振器常被用與微振動隔振，主要因為其具有工作穩(wěn)定、成本低、可以抑制共振峰等特點，但是研究也表明，兩參數(shù)隔振器在隔振區(qū)的衰減率僅為20 dB，而且對高頻干擾（如100 Hz以上的振動），隔離效果并不理想。因為隔振器存在駐波效應，隨著頻率的增高，高頻區(qū)會出現(xiàn)一系列波峰，從而削弱隔振效果。在被動隔振中，一般通過增加隔振級數(shù)來提高隔振器的隔振性能，其中雙層隔振系統(tǒng)最常用。一種特殊的兩級隔振——Zerner隔振，在隔振區(qū)具有40 dB的衰減率。兩級隔振的優(yōu)點是可以獲得更高的頻率衰減特性，但其設(shè)計較困難，結(jié)構(gòu)較復雜，而且較難獲得最優(yōu)值[1]。

對于Zerner隔振，國外研究較早，如LIN Y等人對由膜片泵彈簧和阻尼構(gòu)成的系統(tǒng)進行分析[2]；Davis P在衛(wèi)星隔振平臺中采用了Zerner隔振器，并對其原理進行了簡單闡述[3]；Davis L P在前人工作的基礎(chǔ)上，總結(jié)了Zerner隔振和兩參數(shù)隔振的優(yōu)缺點[4]。Davis T在多軸主被動混合隔振中采用了隔振器，從而使平臺具有更低的隔振頻率[5]。Wilson研究了在D-strut結(jié)構(gòu)上采用Zerner隔振和兩參數(shù)隔振的隔振效果[6]。

本文在隔振器機理與參數(shù)分析的基礎(chǔ)上，提出一種Zerner隔振器，并通過實驗研究了其對微振動的隔離效果及參數(shù)依賴性。

1 隔振器系統(tǒng)模型分析

考慮圖1所示的隔振模型，其振動方程為

其中M表示質(zhì)量，Ca是阻尼，Ka為平行主剛度，Kb為串聯(lián)剛度。

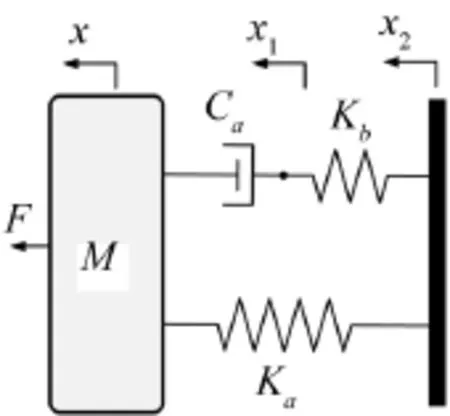
圖1 隔振模型

對方程（1）兩邊求導

綜合方程（1）、（2）、（3），得到方程（4）

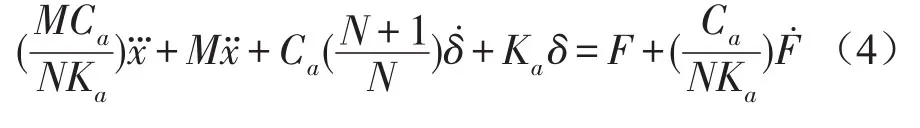
其中假設(shè)Kb=NKa，δ=x-x2，N為剛度比。

對方程（4）兩邊同時進行傅里葉變換，可以得到傳遞函數(shù)[5]

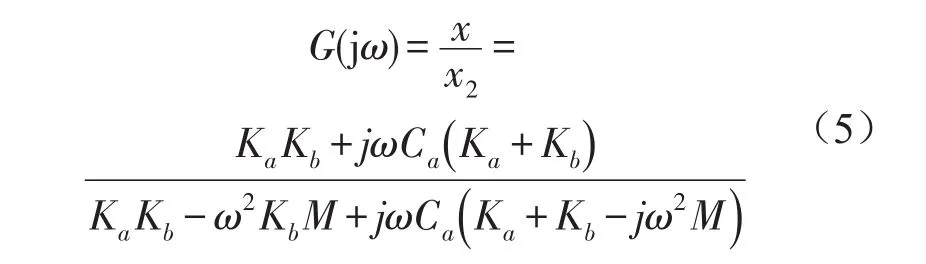
當系統(tǒng)輸入為基礎(chǔ)激勵時，通過方程（4）也可以得到頻響函數(shù)的另一種形式[1]

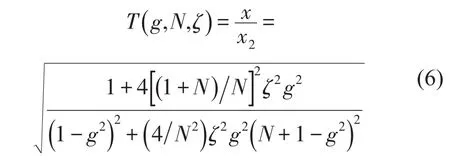
其中g(shù)為頻率比，ζ為阻尼比。

式（6）以參數(shù)N為常數(shù)，參數(shù)（ζ，g）為變量求解隔振系統(tǒng)頻響函數(shù)最優(yōu)值得[3]

式（9）中的ω可利用式（10）和（11）進一步簡化，只包含隔振器參數(shù)

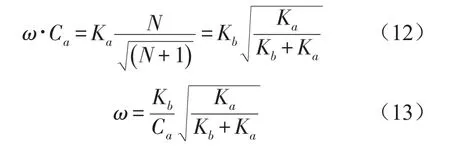
式（13）是隔振系統(tǒng)在最優(yōu)阻尼下的共振頻率表達式。

2 隔振器設(shè)計和實驗

隔振器結(jié)構(gòu)如圖2所示，實物如圖3所示。

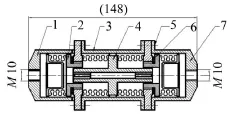
圖2 隔振器結(jié)構(gòu)圖

圖3 隔振器實物圖

隔振器的剛度元件選取波紋管，由圖2可以看到，零件1和2之間的波紋管相當于理論模型中Kb，零件3和5之間的波紋管相當于理論模型中的Ka，Ca阻尼是由阻尼孔和黏滯流體流動產(chǎn)生。

波紋管的厚度是變化的，實測波峰處厚度約為0.10 mm，波谷處厚度約為0.15 mm，波紋管內(nèi)圓環(huán)殼的厚度，可利用經(jīng)驗公式得到近似值。黏滯流體采用的是水，在25°時它的標準運動黏度是1 cst[7]。

2.1 隔振器剛度特性

利用MTS電液式萬能試驗機（50 kN）分別對28個波的波紋管和隔振器的主剛度進行測試，圖4為剛度測試圖。

圖5為波紋管的力—位移曲線，由圖可以看出，波紋管的剛度具有線性特性。由軸向變形（10 mm）和軸向力（約為42 N）可以計算出半波的實際剛度

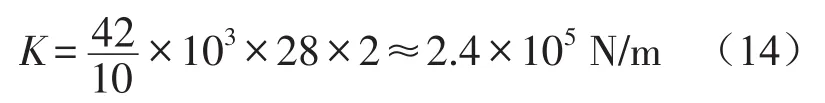
圖4 利用試驗機測試剛度圖

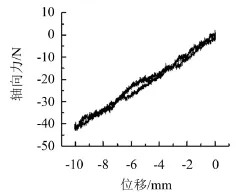
圖5 U型波紋管力位移曲線

圖6是隔振器主波紋管的力—位移曲線，由此可以計算出主波紋管的剛度Ka

圖6 主波紋管力—位移曲線

由式（16）計算可知，隔振器的主波紋管相當于兩個具有3個波的波紋管并聯(lián)，m表示主波紋管的波數(shù)，這與實際結(jié)構(gòu)相符

式（14）、（15）和（16）表明實測結(jié)果比較準確，利用相同方法，可以得到Kb

2.2 隔振器的傳遞特性測試

測試系統(tǒng)如圖7a所示，包括電磁激振臺、加速度傳感器和數(shù)據(jù)采集儀等，圖b為隔振器和質(zhì)量塊在激振平臺安裝方式以及兩個加速度傳感器的安裝位置。

測試原理如圖7a所示，采用基礎(chǔ)激勵，通過兩個加速度傳感器的測量信號得到單級隔振的頻響函數(shù)。

圖7 隔振系統(tǒng)位移傳遞率測試原理圖

在電磁振動臺上進行隔振器的傳遞特性測試。首先，測試僅有主波紋管的隔振系統(tǒng)的傳遞特性，結(jié)果如圖8所示，共振頻率為22.0 Hz，共振峰值約為48 dB，隔振系統(tǒng)的阻尼很小。其次，分別用4 kg、6 kg、15 kg、17 kg、19 kg、25 kg的質(zhì)量塊與隔振器一端聯(lián)接，隔振器另一端安裝在水平振動臺面上，使之組成一個隔振系統(tǒng)。振動臺激勵為1 Hz～200 Hz范圍內(nèi)正弦掃描，分別采用了降頻和升頻兩種模式，并且進行了重復性驗證。隔振器的加速度傳遞特性如圖8所示，由圖中可以看出，隨著質(zhì)量的增大，共振峰向左側(cè)移動，峰值先降低再增大[10，11]，其中實線為阻尼器自身無阻尼時的頻響函數(shù)。

隔振器存在兩個共振頻率，其物理意義的分析可以從結(jié)構(gòu)入手，如圖1所示，當結(jié)構(gòu)中阻尼為0時，整個系統(tǒng)只有Ka起作用，系統(tǒng)的固有頻率計算方程如式（18），定義為第一固有頻率，當結(jié)構(gòu)中的阻尼為無窮大時，Kb和質(zhì)量相當于剛性連接，整個系統(tǒng)簡化為Ka和Kb并聯(lián)，系統(tǒng)的固有頻率計算如式（19），定義為第2固有頻率。

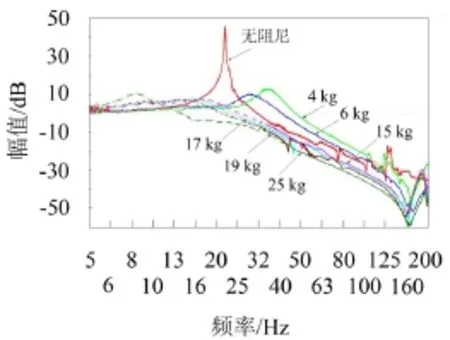
圖8 不同隔振質(zhì)量的加速度傳遞特性曲線

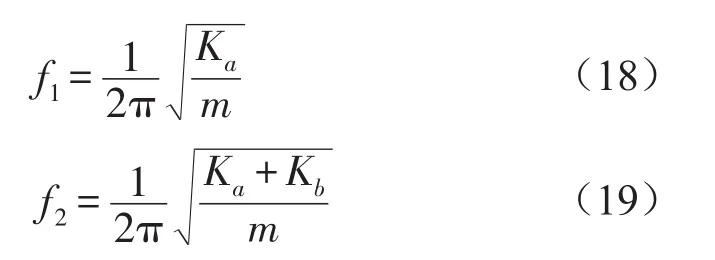
圖8中的數(shù)據(jù)與表1對應，表1中數(shù)據(jù)包括不同質(zhì)量下隔振系統(tǒng)的第1和第2固有頻率，可以看出，實際的共振頻率都處在第1和第2固有頻率之間，隨著質(zhì)量的增大，共振頻率從第2固有頻率向第1固有頻率靠近，同時在這個過程中會出現(xiàn)最優(yōu)阻尼比的特殊情況。表1也給出了共振幅值，質(zhì)量變化時，T也不斷變化，但是從表中可以得到隔振系統(tǒng)的Tmin最小值約為2.2，這時系統(tǒng)的輸出阻尼達到最優(yōu)值。

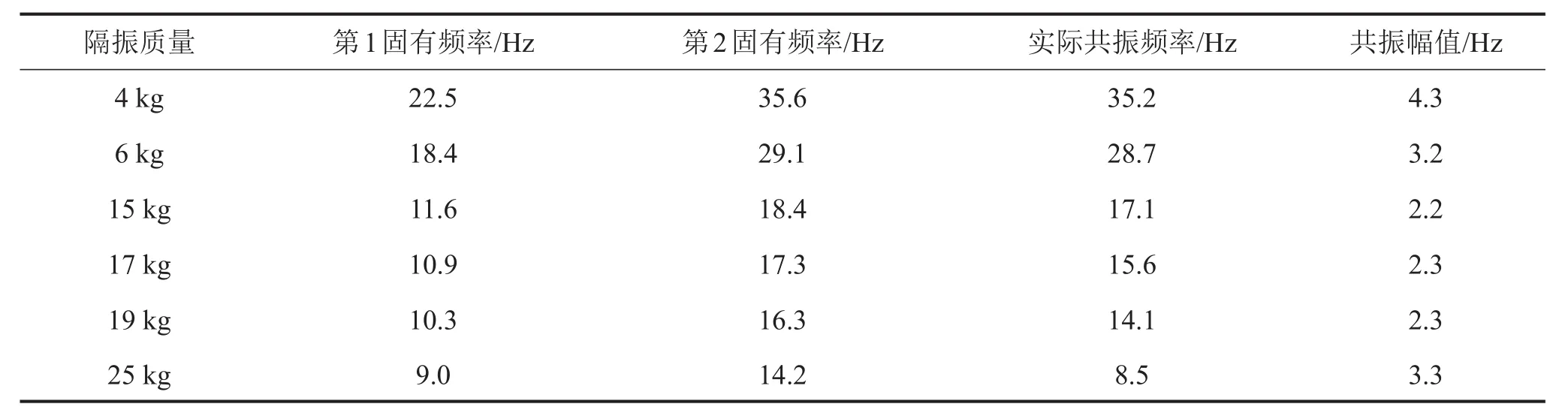
表1 不同隔振質(zhì)量下系統(tǒng)的固有頻率的理論值與實測值

由公式（7）可以知，此時隔振系統(tǒng)的理論峰值應為

其中N為剛度比，隔振器的實際剛度比約為1.5，代入式（20）可得，T=2.3。由此可以看出，理論結(jié)果與實驗結(jié)果吻合良好。

通過理論分析可知，隔振系統(tǒng)負載質(zhì)量取一個確定的值時，隔振系統(tǒng)會取到最優(yōu)阻尼，但是在實際應用當中，在滿足設(shè)計要求前提下，系統(tǒng)的負載質(zhì)量并不需要完全和理論值精確相等，只要在一個范圍之內(nèi)即可，從表1中可證實這個想法，可看出當質(zhì)量從4 kg～25 kg遞增時，系統(tǒng)振幅變化規(guī)律是從大到小，然后再變大。

假定阻尼器設(shè)計要求中規(guī)定振幅范圍是不大于2.3時，通過表1可以知道，只要負載質(zhì)量在15 kg～19 kg之內(nèi)，所設(shè)計的隔振器就滿足要求。

3 結(jié)語

本文得到隔振系統(tǒng)在最優(yōu)阻尼比下的共振頻率表達式。實驗測試與理論計算結(jié)果相符，說明隔振器設(shè)計有效。隔振器在共振峰處的放大因子可以按公式預估。

[1]丁文鏡.減振理論[M].北京：清華大學出版社，1988.

[2]Lin Y,Cunningham D.Stiffness and stress of a fluid-filled circular diaphragm[J].AIAAjournal,1992:1504-1513.

[3]Davis P,Cunningham D,Harrell J.Advanced 1.5 Hz passive viscous isolation system[C].Proceeding of the 35 th AIAA/ASME/ASCE/AHS/ASC Structures.Structural Dynamics and Materials Conference.America:1994.2655-2665.

[4]Davis L P,Carter D R,Hyde T T.Second-generation hybrid D-strut[J].International Society for Optics and Photonics,1995:161-175.

[5]Davis T,Davis L P,Sullivan J M,et al.High-performance passive viscous isolator element for active/passive(hybrid)isolation[C].Symposium on Smart Structures and Materials.International Society for Optics and Photonics. Amecria:1996.281-292.

[6]Wilson G W,Wolke P J.Performance prediction of D-Strut isolation systems[C].Smart Structures and Materials 97 International Society for Optics and Photonics.America: 1997.236-250.

[7]劉德金.波紋管液壓成形工藝的設(shè)計計算[J].儀表技術(shù)與傳感器,1976,2(2):44-49.

Analysis and Experiment of Isolators for Micro-vibration Control

MA Jun
（Military Representative Office in 431 Factory,Huludao 125004,Liaoning China）

The expression of the optimal frequency response of an isolation system was obtained through the analysis of its frequency response function.Based on the result,an isolator for micro-vibration control was designed and its performance was tested.Vibration acceleration and minimum transmissibility rate of the isolation system with different mass components and the isolator were measured.The test results were in a good accordance with those of calculation,which indicate that the design of the isolator is correct and effective.

vibration and wave;isolator;micro-vibration;optimal frequency response function;bellows

TB535+.1

A

10.3969/j.issn.1006-1335.2015.02.045

1006-1355(2015)02-0205-04

2014－10－29

馬俊（1979－），男，遼寧遼陽人，海軍駐葫蘆島431廠軍事代表室，工程師，從事艦船的監(jiān)造工作。E-mail:hhj@sjtu.edu.cn