空濾器結構優化和輻射噪聲分析

彭卓凱，鄧志強，黃振邦

（大長江集團 研發中心，廣東 江門 529030）

空濾器結構優化和輻射噪聲分析

彭卓凱，鄧志強，黃振邦

（大長江集團 研發中心，廣東 江門 529030）

針對試驗中發現的空濾器殼體輻射噪聲大問題，綜合運用模態計算、進氣壓力頻譜計算、拓撲優化、形貌優化和聲學有限元法解決了該問題。首先，通過模態計算，得出了空濾器外殼的各階振型和模態頻率。接著分析了發動機的進氣壓力波頻譜，找出了進氣壓力較大的頻段，由此可知空濾器輻射噪聲大是由于第1階頻率較低引起的。然后，通過拓撲優化和形貌優化，找出了筋的最佳布置位置，使空濾器外殼的第1階頻率得到大幅提高。最后，通過輻射噪聲的計算，確認了改進后的空濾器外殼的總聲功率級降低了13.8 dB，噪聲改進效果非常明顯。

聲學；空濾器；進氣壓力；優化；輻射噪聲；有限元法

摩托車空濾器是發動機進氣系統的一個重要組成部分，其作用是預先對進入氣缸的空氣過濾，防止灰塵或沙粒進入氣缸，以減少氣缸、活塞、活塞環的磨損，延長發動機的工作壽命。在現代摩托車的空濾器結構設計中，還注重進氣消聲；另外，空濾器還具有優化匹配發動機性能的作用[1,2]。

空濾器大體由兩部分組成：空濾器殼體和濾芯。為了達到較好的濾清效果和減少過濾時對空氣的阻力以及增大儲灰能力，空濾器應設計得盡量大一些。但當空濾器較大時，在進氣壓力波的激勵下，空濾器殼體容易發生共振而發出較大的噪聲。某空濾器在試驗過程中被發現其外殼體輻射噪聲較大，此時，發動機轉速在6 000 r/min左右。現本文綜合運用模態計算、進氣壓力頻譜計算、拓撲優化、形貌優化和聲學有限元法來解決該問題。

1 空濾器模態計算

試驗時出現共振的空濾器外殼體如圖1、2所示，該件通過6個安裝點與空濾器內殼體組裝在一起。為解決該共振問題，首先對空濾器外殼體進行模態分析。將在NX軟件中建好的3D模型導入有限元分析軟件Nastran中，進行網格劃分，采用2 mm二階四面體單元。接著定義部件的材料屬性，材料為PP塑料，彈性模量為1 000 MPa，泊松比為0.41，密度為890 kg/m3。再定義邊界條件，將6個安裝孔約束住。最后定義模態提取分析步，提取1 000 Hz以前的所有模態。計算出的原始空濾器外殼的模態頻率見表1，第1階模態振型見圖3，從該振型可知，中部的圓形區域振幅最大。從計算出的模態頻率和振型看，第1階模態頻率較低是造成輻射噪聲大的主要原因，因為在進氣壓力波的激勵下，空濾器外殼會發生共振。為進一步驗證該推斷，下面進行進氣壓力頻譜計算。

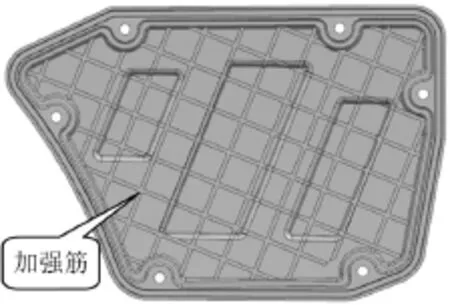
圖1 原始空濾器外殼（里側）

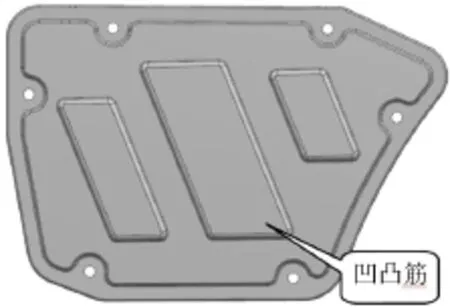
圖2 原始空濾器外殼（外側）

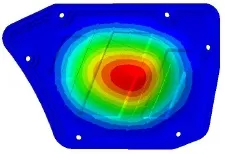
圖3 原始空濾器外殼第1階振型

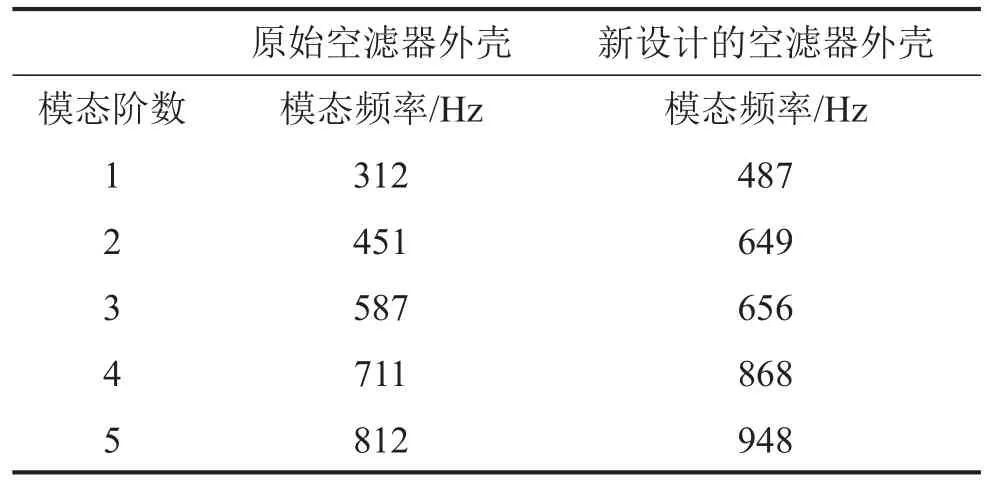
表1 改進前、后的空濾器外殼模態頻率

2 進氣壓力頻譜計算

該發動機為125 ml排量的單缸自然風冷發動機。在發動機模擬分析軟件boost中，對該發動機進行建模，設置相應的進氣系統、燃燒系統、排氣系統等參數，在空濾器內設置壓力監測點，測量發動機轉速在6 000 r/min時空濾器內壓力隨曲軸轉角的變化關系，并將此壓力在時域內的信號通過快速傅里葉變換（FFT）轉換為頻域信號[3]。在6 000 r/min時，空濾器內壓力的頻譜如圖4所示。

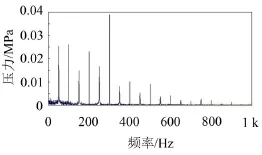
圖4 空濾器內壓力在6 000 r/min時的頻譜

從該圖可知，在300 Hz和低于300 Hz的區域，空濾器內壓力較大，在高于300 Hz的區域，空濾器內壓力隨頻率增加而逐漸減小。從上面的模態計算可知，空濾器外殼體第1階模態頻率為312 Hz，這個頻率位于進氣壓力較大的頻域范圍附近，故而會出現共振而產生較大的輻射噪聲。

3 拓撲優化和形貌優化

優化設計有三要素，即設計變量、目標函數、約束條件。設計變量是在優化過程中發生改變從而提高性能的一組參數。目標函數就是要求的最優性能，是關于設計變量的函數。約束條件是對設計的限制。目標函數、約束函數是從有限元分析中獲得的結構響應。設計變量的選擇依賴于優化類型。在拓撲優化中，設計變量是單元的密度，在形貌優化中，設計變量為形狀擾動的線性組合因子[4]。拓撲優化能在給定的設計空間內尋求最佳的材料分布。形貌優化是一種形狀最佳化的方法，即在板形結構中尋找最優的凹凸型加強筋的分布，與拓撲優化不同的是，形貌優化不刪除材料。

從以上的模態和進氣壓力頻譜分析的結果可知，空濾器外殼體第1階模態頻率低，從而出現了共振問題。故提高第1階模態頻率可解決該問題。從原始空濾器外殼體的3D模型看（見圖1、2），其上面布置了大量的網狀加強筋，且還帶有3個四邊形的凹凸筋。從提高模態頻率的角度考慮，這些加強筋和凹凸筋的形狀和位置未必是合理的。為了找到最佳的加強筋和凹凸筋的布置位置，現對空濾器外殼體進行拓撲優化和形貌優化，以提高其第1階模態頻率。其中，拓撲優化用于確定加強筋（增加材料的筋）的最佳布置，形貌優化用于確定凹凸筋（不增加材料的筋）的最佳布置。

將原始的加強筋和凹凸筋都去除，再用優化計算重新布置這些筋。優化計算的模型采用1 mm四邊形殼單元，如圖5所示，其中灰色區域為設計區域（可優化區域），邊緣黑色區域為非設計區域。優化目標為第1階模態頻率最大。在拓撲優化計算中，加強筋高度設為3.5 mm。在形貌優化計算中，凹凸筋的深度設為3 mm，起筋角度設為60°。

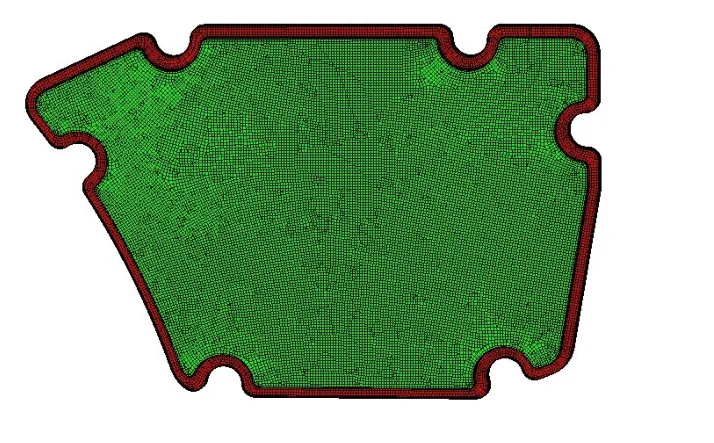
圖5 空濾器外殼優化計算模型

形貌優化計算結果見圖6，其中，除黑色以外的白色區域和灰色區域為最佳的凹凸筋布置位置。從圖可知，凹凸筋應布置在外殼的中部，呈近似橢圓形。而原始空濾器外殼的凹凸筋為間隔一定距離的3個四邊形，與優化結果有較大差異，這表明，原始凹凸筋的設計不盡合理。

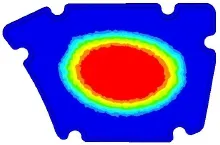
圖6 空濾器外殼形貌優化結果

拓撲優化計算結果見圖7，其中，除黑色以外的灰色區域和接近灰色的白色區域為最佳的加強筋布置位置。從圖可知，加強筋應布置在外殼的邊緣，中間的大部分區域都無需布置加強筋。而原始空濾器外殼的加強筋呈網狀密布，與優化結果差異大，這表明，原始加強筋的設計既浪費材料也不利于提高模態頻率。

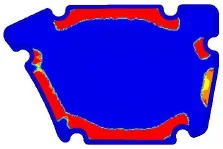
圖7 空濾器外殼拓撲優化結果

現根據拓撲優化和形貌優化計算結果，對空濾器外殼的加強筋和凹凸筋重新設計，重新設計后的3D模型如圖8所示。

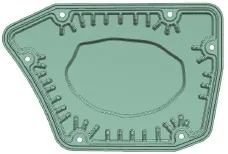
圖8 重新設計后的空濾器外殼

4 空濾器輻射噪聲計算

4.1 模態和動態響應計算

為進一步確認改進前、后的空濾器外殼的聲學響應特性，現進行輻射噪聲的分析。空濾器外殼在進氣壓力波的激勵下，表面會產生振動，從而發出噪聲。故首先須計算空濾器外殼表面的振動響應。對于帶阻尼的多自由度系統，其受迫振動的微分方程為

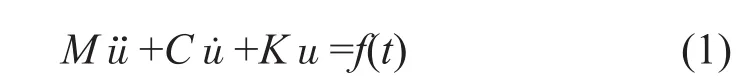
解這個運動方程一般有兩種方法，一種是直接積分法，就是按時間歷程對上述微分方程直接進行數值積分；另一種解法是模態疊加法[5,6]。對于計算系統在諧波激勵下的線性響應，后一種基于模態的計算方法比直接積分的方法計算速度更快。故本文采用模態疊加法計算空濾器外殼表面的振動速度。首先須計算空濾器外殼的模態，再基于模態結果計算空濾器外殼在進氣壓力波激勵下的振動速度。改進后空濾器外殼的結構有限元模型見圖9，采用2.5 mm二階四面體單元。改進前、后的空濾器外殼模態頻率見表1，從該表可知，在不增加空濾器外殼基本壁厚的前提下，僅僅改變筋的布置，其第1階模態頻率已經由312 Hz大幅提高到了487 Hz。

圖9 改進后空濾器外殼的結構有限元模型

4.2 輻射噪聲計算

為求解流場中任意位置（x,y,z）處的聲壓p，可通過流體的連續方程、運動方程、能量方程、物態方程推導出Helmholtz聲學波動方程，其表達式為[7]

?2p(x,y,z)-k2p(x,y,z)=-jρ0ωq(x,y,z)

式中k為波數，ω為角頻率，ρ0為定常流動下的密度，q體積速度。用數值方法求解Helmholtz方程的常用方法有聲學有限元法（FEM）和聲學邊界元法（BEM）。當模型不是特別大時，有限元法在計算內聲場和輻射噪聲方面的速度更快，故本文采用有限元法。用有限元法求解Helmholtz方程時，首先需要把計算的聲場離散成一定數量的小聲場，每個小聲場稱為單元，單元之間用節點連接。對于三維聲場，常用的單元有四面體單元和六面體單元。

本文采用3 mm四面體單元對空濾器外殼周圍的聲場進行離散，聲學網格模型的截面圖見圖10。

并以空濾器外殼為中心布置半徑為1 m的球面場點（見圖11），以計算該球面場點上的輻射聲功率。將上一步計算的空濾器外殼的表面振動速度導入聲學計算軟件LMS Virtual Lab，將表面振動速度映射到聲學網格上作為輻射噪聲計算的邊界條件，求得改進前、后的空濾器外殼的輻射聲功率如圖12所示。從計算結果可知，原始空濾器外殼在312 Hz和739 Hz附近出現了聲功率峰，312 Hz處的最大聲功率級為127.2 dB。新設計的空濾器外殼在492 Hz和882 Hz附近出現了聲功率峰，492 Hz處的最大聲功率級為112.5 dB。對比模態計算結果可知，改進前、后的空濾器外殼的聲功率峰都出現在第1階和第4階模態頻率附近。原始空濾器外殼在整個頻段的總聲功率級為133 dB，新設計的空濾器外殼在整個頻段的總聲功率級為119.2 dB。總聲功率級降低了13.8 dB；最大聲功率級降低了14.7 dB。從以上輻射噪聲的計算結果可知，噪聲改進效果非常明顯。

圖11 球面場點

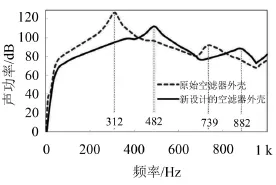
圖12 改進前、后的空濾器外殼的輻射聲功率

5 結語

（1）通過模態計算和進氣壓力波計算，得出了空濾器外殼的各階振型和模態頻率以及進氣壓力較大的頻段，找出了空濾器外殼輻射噪聲大的原因；

（2）通過拓撲優化和形貌優化，找出了筋的最佳布置位置，使空濾器外殼的第1階頻率得到大幅提高；

（3）通過輻射噪聲的計算，進一步確認了空濾器外殼的改進效果：總聲功率級降低了13.8 dB。噪聲改進效果非常明顯。

以上分析流程及相關的模擬計算方法為快速、準確地解決輻射噪聲大問題提供了解決方案，減少了費時費力的試驗，也節約了部件的材料成本（相對將部件簡單的加厚的對策方案），對解決類似的車輛部件輻射噪聲大問題具有一定的參考價值。

[1]馮超，鄔惠樂.汽車工程手冊摩托車篇[M].北京：人民交通出版社，2001.330-331.

[2]曾憲錚，吳振根.中外流行摩托車構造使用維修[M].長沙：湖南科學技術出版社，1996.164-165.

[3]朱訪君，吳堅.內燃機工作過程數值計算及其優化[M].北京：國防工業出版社，1997.89-143.

[4]張勝蘭，鄭冬黎.基于Hyper Works的結構優化設計技術[M].北京：機械工業出版社，2007.159-163.

[5]許本文，焦群英.機械振動與模態分析基礎[M].北京：機械工業出版社，1998.70-78

[6]劉延柱，陳文良，陳立群.振動力學[M].北京：高等教育出版社，1998.85-90.

[7]李增剛，詹福良.Virtual.Lab Acoustics聲學仿真計算高級應用實例[M].北京：國防工業出版社，2010.4-17.

Structure Optimization and Radiation NoiseAnalysis of Air Cleaners

PENG Zhuo-kai,DENG Zhi-qiang,HUANG Zhen-bang
（Research&Development Center,Dachangjiang Group,Jiangmen 529030,Guangdong China）

Modal calculation,frequency spectrum calculation of intake pressure,topology analysis,topography analysis and acoustic FEM were employed to solve the serious radiation noise problem of an air cleaner’s shell.Firstly,vibration modes and eigen-frequencies of the air cleaner shell were obtained by modal computation.Secondly,the intake pressure spectrum was analyzed and the frequency zone with large intake pressure was determined.It was found that the large radiation noise of the air cleaner was resulted from the low 1st order frequency.Finally,the optimal position of the ribs was discovered by topology and topography analysis,so that the 1st order frequency of the air cleaner could be enhanced greatly. The result of the radiation noise computation show that the total sound power level of the air cleaner can be reduced by 13.8 dB after the modification and the improvement effect is very obvious.

acoustics;air cleaner;intake pressure;optimization;radiation noise;finite element method

TB53

A

10.3969/j.issn.1006-1335.2015.02.049

1006-1355(2015)02-0222-04

2014－10－17

彭卓凱（1979－），男，碩士，主要從事摩托車及其發動機的CAE和NVH分析。E-mail:pengzhuokai@126.com