高維雙轉子系統的碰摩響應特性研究＊

羅貴火，楊喜關，2，王 飛

（1.江蘇省航空動力系統重點實驗室，南京航空航天大學能源與動力學院，江蘇 南京210016；2.中國人民解放軍94655部隊，安徽 蕪湖241000）

引 言

含中介支承的雙轉子系統被航空發動機廣泛采用，高性能的追求使發動機轉靜子間的間隙越來越小，轉、靜子碰摩是航空發動機的典型故障之一。研究高維雙轉子系統中轉、靜子碰摩故障對系統響應特性的影響，對航空發動機碰摩故障的診斷和識別有著重要的意義。

含碰摩故障的雙轉子系統動力特性的研究一直被相關學者所關注。晏礪堂從理論和試驗兩方面研究了航空雙轉子發動機轉、靜件碰摩的振動特征［1］。孟越和李其漢應用整體傳遞系數法分別模擬了單轉子、雙轉子的碰摩故障，研究了單轉子和雙轉子系統的碰摩故障特征［2］。單穎春利用接觸理論和ANSYS軟件得到了碰摩力模型，并與整體傳遞系數法相結合建立了含碰摩故障的雙轉子系統的動力學方程，得到了相關的故障特征［3］。周海侖以航空發動機雙轉子系統的為研究對象，建立了含碰摩故障的雙轉子－滾動軸承－機匣耦合動力學模型［4］。韓清凱基于剛柔多體模型，在MSC.Adams中建立了含碰摩故障的雙轉子系統動力學模型，對其非線性特性進行了研究［5］。袁惠群利用連續體理論，建立了雙轉子－機匣耦合系統碰摩模型［6］。陳松霆等采用拉格朗日法建立了含轉、靜件碰摩故障的反向旋轉雙轉子系統的動力學模型［7］。

高維轉子系統的建模方法和模型縮減方法，也一直是熱門的研究方向。在雙轉子系統的研究中，為了減小計算規模，引入了模態綜合法。1980年，美國學者Glasgow D A［8］，將固定界面子結構模態綜合法應用多轉子系統的動力特性分析中。隨后，Li D F和Wang W開展了自由界面模態綜合法在雙轉子系統動力特性分析中的應用研究［9～11］。近年來，國內外的許多學者開展了復雜雙轉子系統的非線性動力學建模研究。2010年，鄧四二利用有限元方法建立同向旋轉雙轉子－滾動軸承耦合系統的非線性動力學數學模型［12］；陳果針對航空發動機整機振動，利用有限元方法對轉子和機匣系統進行建模，建立了一種通用的復雜轉子－支承－機匣耦合動力 學 模 型［13］。 英 國 學 者 Hai，Pham Minh 和Bonello，Philip考慮擠壓油膜阻尼器非線性特性的影響，在模態綜合法的基礎上，分別從時域和頻域兩個方面開展了整機建模方法的研究［14，15］。

本文以某雙轉子試驗器為研究對象，利用有限元方法和自由界面模態綜合法建立含局部碰摩故障的雙轉子系統的動力學模型。為提高計算效率，利用單位脈沖響應和Duhamel積分的方法，進行數值求解。在此基礎上，分析了含碰摩故障的反向旋轉雙轉子系統的動力學響應特性。

1 雙轉子系統模型

1.1 研究對象

為研究雙轉子系統的動力特性，根據現有航空發動機中的五支點的雙轉子系統的結構特點，設計了雙轉子試驗器，圖1為試驗器的結構簡圖。軸承Ⅰ、Ⅱ、Ⅲ、Ⅳ、處均采用“軸承＋鼠籠式彈性支承＋擠壓油膜阻尼器”的結構，中介軸承Ⅴ的內環和外環直接與內轉子和外轉子連接。

考慮支承Ⅰ、Ⅱ、Ⅲ、Ⅳ處的擠壓油膜阻尼器非線性油膜力和中介軸承Ⅴ的非線性軸承力，并假定軸承Ⅰ、Ⅱ、Ⅲ、Ⅳ處的鼠籠式彈性支承為線性支承，假定軸承Ⅰ、Ⅱ、Ⅲ、Ⅳ為剛性。同樣考慮內、外轉子各輪盤處的不平衡力和陀螺效應，忽略重力和材料阻尼的影響。假設轉子碰摩故障發生在輪盤處，用ω1和ω2分別表示內、外轉子的轉速，內、外轉子以一定的轉速比λ＝ω2／ω1運轉。

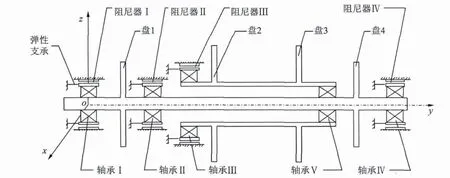
圖1 五支點雙轉子系統結構簡圖Fig.1 Structure diagram of dual－rotor system with five supports

1.2 動力學方程

采用有限元方法，根據系統特點建立雙轉子系統動力學方程。并將各非線性支承處的鼠籠力、非線性油膜力、非線性軸承和陀螺力矩作為外力移到方程的右邊，考慮碰摩力和不平衡力的影響，并假設有限元模型的節點個數為n，則運動方程可寫為

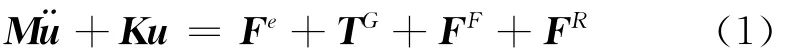
式中M∈R4n×4n，K∈R4n×4n分別為系統質量矩陣和剛度矩陣；Fe∈R4n×1，TG∈R4n×1分別為不平衡力向量和陀螺力矩向量；FF∈R4n×1，FR∈R4n×1分別為非線性支承處的作用力向量和非線性碰摩力向量；u＝［x1，z1，θx1，θz1，…，xn，zn，θxn，θzn］T∈R4n×1為系統位移向量。

用F表示不平衡力向量、非線性支承處的作用力向量和非線性碰摩力向量的和，則

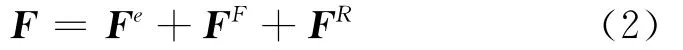
用集合θ表示陀螺力矩作用處自由度集合（TG中非零元素對應的自由度集合），用集合f表示除陀螺力矩外的系統外部作用力處的自由度集合（F中非零元素對應的自由度集合），用集合N表示系統非線性力作用處的自由度集合（非線性支承處的作用力和碰摩力作用處的自由度集合），用集合L表示f與N的差集，用集合E表示系統全體自由度與f和θ的差集。則

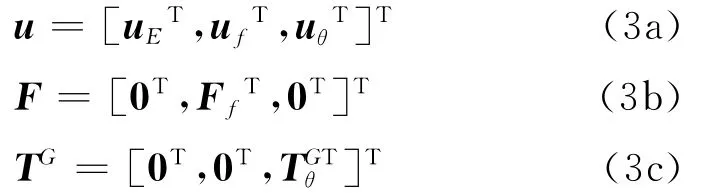
陀螺力矩向量TGθ有如下的表達式

［16］利用赫茲接觸理論建立中介軸承的非線性力模型；參考文獻［17］采用短軸承理論，建立各支承處的擠壓油膜阻尼器非線性力模型；參考文獻［4］建立輪盤碰摩力的非線性力模型。由于中介軸承的非線性軸承力、擠壓油膜阻尼器非線性油膜力和非線性碰摩力的表達式中無加速度項，則

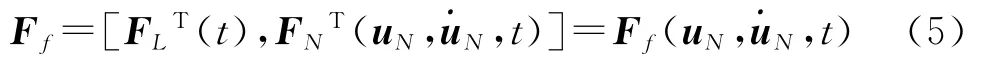
1.3 模態縮減

采用自由界面模態綜合法對系統進行維數的縮減。引入模態坐標變換，忽略剩余模態的影響，可得位移向量與模態坐標向量的轉換關系

式中q為模態坐標，Φ為支承界面為自由狀態時系統質量歸一化后的模態振型，利用ANSYS軟件進行模態振型Φ的獲取。

將坐標變換關系式（6）代入物理空間中的運動方程（1），并利用模態振型的正交化特性，可以獲得模態空間中的運動方程

式中Ωr（r＝1…k）為第r階模態頻率，k為保留模態的階數，Φf和Φθ分別為自由度集合f和θ對應的模態振型矩陣。

方程（7）的各階模態運動方程與單自由度系統在外部激勵下的運動方程有著類似的形式。假定零時刻的位移和速度初始條件為q0和，則利用Du hamel積分，可得方程（7）的模態位移響應

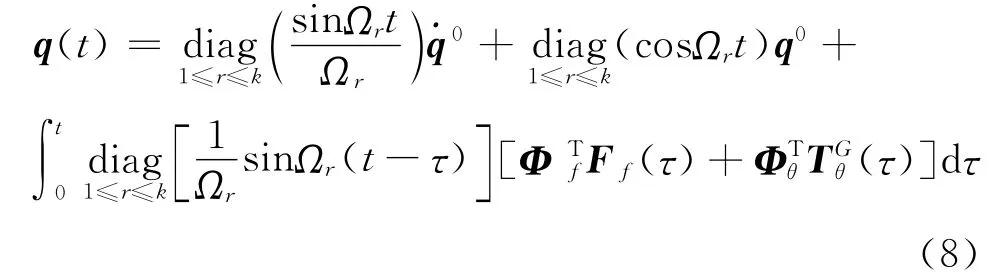
至此，在模態空間中得到了非線性動力系統的瞬態連續解。求解式（8）可得整個系統在模態空間中的響應，由變換關系（6）可得轉子各節點在物理空間中的響應。由于非線性作用力的存在，直接對方程（8）進行積分顯然是不現實的。本文借鑒文獻［1 4］中提出的I RM方法對式（8）進行求解。

2 非線性動力學模型的數值求解算法

取時間區間［tn－1，tn］，其中，tn＝tn－1＋h，用和表示tn－1時刻的響應，用和表示tn時刻的響應。如h的值取的足夠小，當0≤τ≤h時，利用線性差分格式，Ff（τ）和可近似表示為

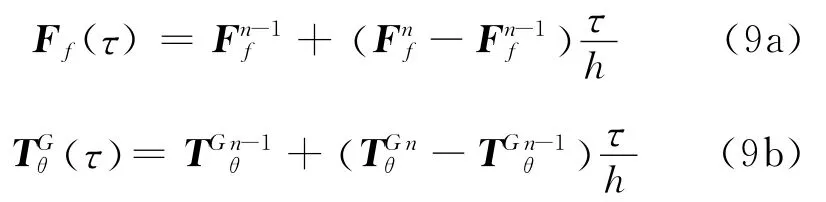
式中

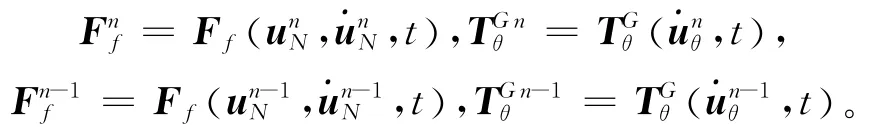
在時間區間 ［tn－1，tn］上，假定tn－1時刻的模態響應qn－1和為初始條件，則利用式（8）可得模態位移響應

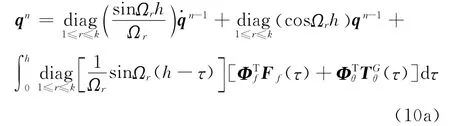
將式（9a）對h進行求導，可得到模態速度響應

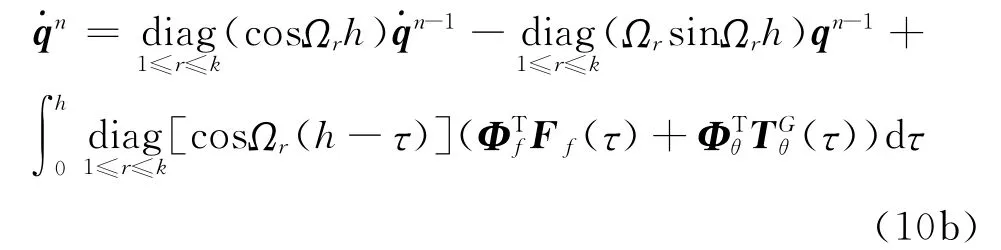
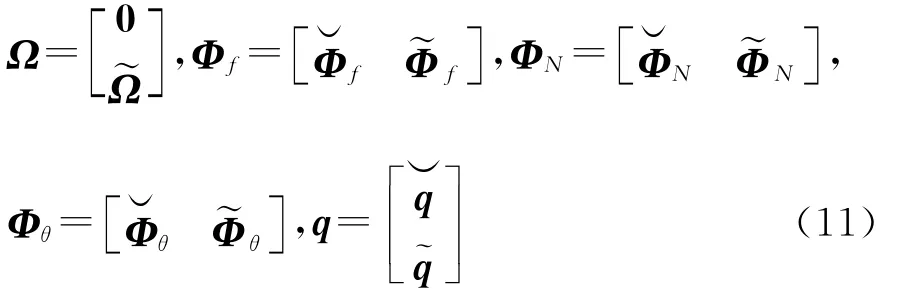
假設自由界面系統有P個剛體模態，則模態參數和坐標有如下表達式：式中Ω包含一個長度為P，數值為零的子向量；和由剛體模態向量組成和由彈性變形模態向量組成和分別為剛體模態坐標和變形模態坐標。

將式（9）代入式（10），并進行積分，可得qn和n的表達式。求解Ωr→0時qn和積分后表達式的極限值，可得到剛體模態對響應qn和的貢獻，經整理可得包含剛體模態影響的qn和的表達式：

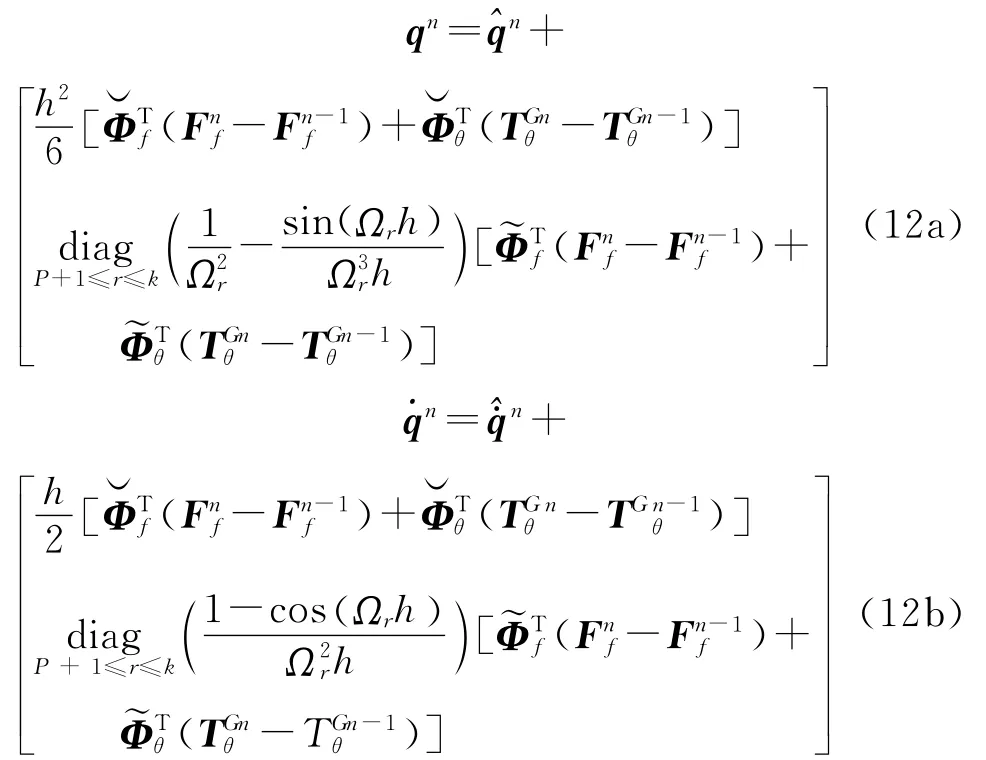
式中

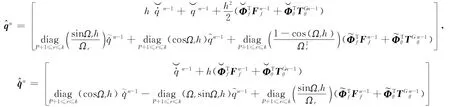
由式（6）所示的物理坐標向量與模態坐標向量的轉換關系，有：

將式（12）和式（4）代入式（13a），并經整理有

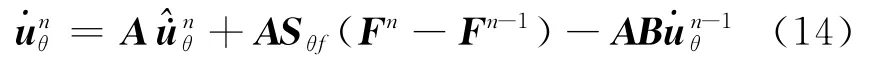
式中

將式（12a）代入式（13b），式（12b）代入式（13c），并代入式（14）的關系，經整理有如下的表達式：

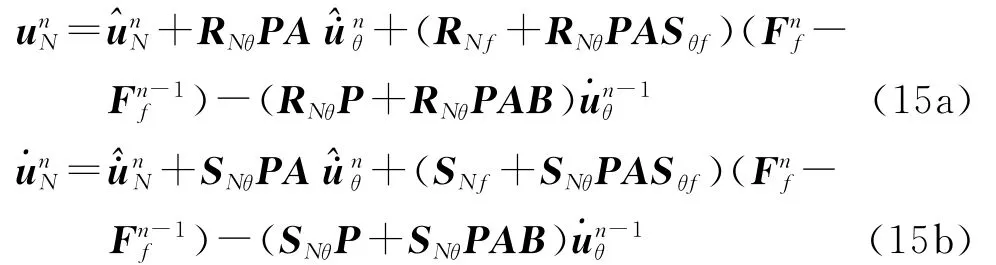
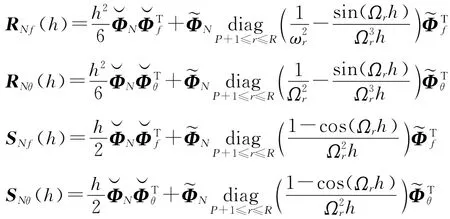
式（12），（14）和（15）組成式（8）的時間迭代公式。故式（1 5）為關于未知數和的非線性代數方程組，采用N e w t o n－R a p h s o n法來求解，可得和，進而由式（1 4）可得。隨后，利用式（1 2）可得tn時刻的模態響應qn和。通過物理坐標與模態坐標之間的轉換關系式（6），可得轉子系統tn時刻任意節點處的位移響應和速度響應。至此，完成［tn－1，tn］時間區間內的計算，將所得到的tn時刻的響應值作為下一時間區間的初始條件，開始新的計算。

非線性方程組（15）的維數等于向量unN個數的兩倍，即等于非線性力處的自由度個數的兩倍，而數值計算的效率主要取決于Newton－Raphson法來求解非線性方程組的效率。所以，在每個時刻非線性方程組的計算規模僅與非線性力處的自由度個數的兩倍有關，可大大提高計算效率。選取足夠多的保留模態個數，可保證計算的精度。

3 雙轉子系統碰摩故障的響應分析

3.1 模型參數

以雙轉子試驗器為參考，給定轉子及其支承系統的參數。在ANSYS中建立雙轉子系統的有限元模型，利用ANSYS模態分析模塊進行自由狀態下的模態分析，獲取轉子系統的模態參數，具體見表1所示。各鼠籠的彈性剛度見表2所示，各輪盤的不平衡量分布見表3所示，各擠壓油膜阻尼器參數見表4所示，中介軸承具體參數見表5所示。

表1 轉子模型相關參數Tab.1 Parameters of dual－rotor system

表2 鼠籠式彈性支承剛度Tab.2 Support stiffiness

表3 各輪盤的不平衡量Tab.3 Unbalance value of every disk

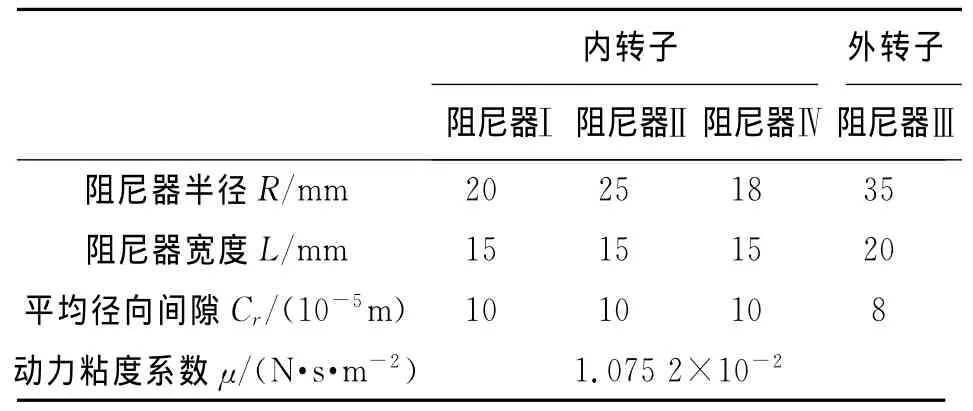
表4 擠壓油膜阻尼器參數Tab.4 Parameters of squeeze film damper

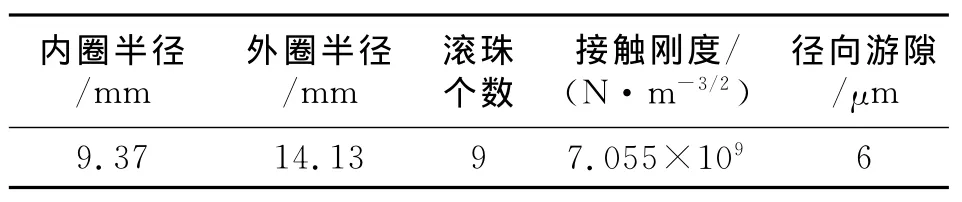
表5 中介軸承的具體參數Tab.5 Parameters of intermediate bearing

3.2 方法驗證

為驗證本文方法的正確性，通過兩種方法來計算雙轉子系統的不平衡響應。方法一：本文方法；方法二：固定界面模態綜合法。方法二［18］為作者的一項前期研究工作，并經過試驗驗證，計算中保留前40階約束主模態，其余系統參數與方法一相同。計算時內、外轉子以轉速比1.6反向旋轉，系統無碰摩。

圖2和3分別為由兩種方法所得到的轉子系統在內轉子轉速230 rad／s（外轉子轉速368 rad／s）時的盤3和盤4處的軸心軌跡圖，兩圖對比可以看出，兩種方法所得到的軸心軌跡有著較好的吻合性，驗證了本文方法的正確性。

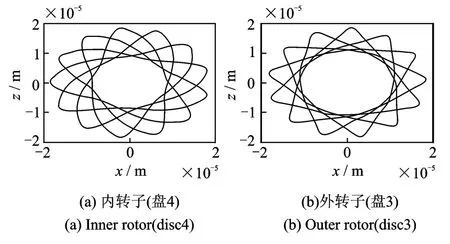
圖2 方法一得到的軸心軌跡圖Fig.2 Orbit obtained by method one

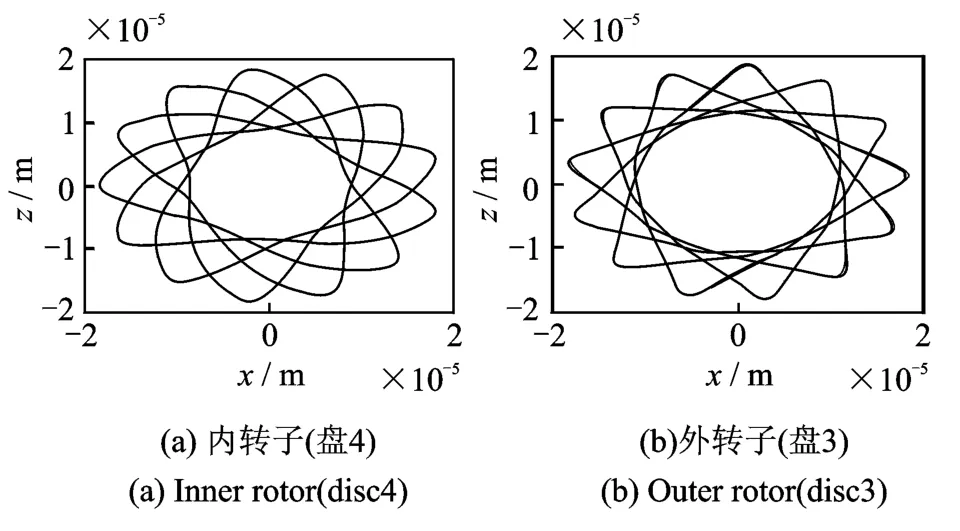
圖3 方法二得到的軸心軌跡圖Fig.3 Orbit obtained by method two

3.3 含碰摩故障反向旋轉雙轉子系統響應特性分析

對于內外轉子存在一定轉速比的雙轉子系統來說，存在分別以內轉子和外轉子為主激勵的兩個一階臨界轉速。假設內外轉子反向旋轉，轉速比取1.6，則在3.1節的模型參數下轉子系統分別以內、外轉子為主激勵的臨界轉速值為：197.5 rad／s和200 rad／s。為分析碰摩故障對反向旋轉雙轉子系統頻率特性的影響，以盤4（內轉子）的響應為例，分析三個典型轉速下的碰摩故障響應特性：外轉子為主激勵的一階臨界轉速前（內轉子110 rad／s，外轉子176 rad／s）、兩個一階臨界轉速之間（內轉子150 rad／s，外轉子240 rad／s）和內轉子為主激勵的一階臨界轉速后（內轉子250 rad／s，外轉子400 rad／s）。圖4，5和6分別為以上三種轉速下的轉子的頻譜圖和軸心軌跡。由圖4～6可以看出：

1）無碰摩力時，三種轉速下響應中，均存在內、外轉子的同步不平衡響應頻率ω1和ω2，且二者占絕對優勢，基本看不到其他頻率成份，軸心軌跡呈規則的“花瓣狀”；

2）各轉速下，碰摩時的軸心軌跡與無碰摩時的軸心軌跡及形狀發生了明顯的變化：外轉子為主激勵的一階臨界轉速前后有明顯削峰和不規則碰摩特點；內轉子為主激勵的一階臨界轉速后軸心軌跡變得雜亂；

3）碰摩故障使系統響應的頻譜圖中出現了較豐富的頻率成分，但同步不平衡響應頻率ω1和ω2仍占主導地位；在低轉速時系統響應中出現了2ω1＋ω2，2ω2＋ω1的頻率成分，但二者的響應幅值較小；在兩個一階臨界轉速之間的轉速時，除2ω1＋ω2，2ω2＋ω1的頻率成分外，又出現了3ω1＋ω2，3ω2＋ω1頻率成分；隨轉速的增加，在大于系統一階臨界轉速后，系統的響應中出現了2ω1＋ω2，2ω2＋ω1，（ω1＋ω2）／2，（ω1＋ω2）／2，（3ω1－ω2）／2，（3ω2－ω1）／2，2ω1－ω2，2ω1＋ω2；在前兩個較低轉速情況下，系統的組合響應頻率均為兩同步不平衡響應頻率的倍頻和，在高轉速情況下，系統響應中出現了兩同步不平衡響應頻率的倍頻差及倍頻差的分頻。

為分析碰摩故障對轉子響應中的同步不平衡激勵頻率幅值的影響，以內轉子5 rad／s和外轉子8 rad／s的轉速增量，計算78個轉速點時系統無碰摩故障和含碰摩故障時的轉子系統穩態響應。圖7為盤3和盤4的響應中兩同步不平衡激勵頻率幅值在無碰摩和碰摩時隨轉速的變化圖。

圖4 外轉子為主激勵的一階臨界轉速前系統無碰摩和碰摩時的頻譜圖和軸心軌跡圖Fig.4 Spectrum and orbit with and without rubbing before the first critical speed excited by outer rotor

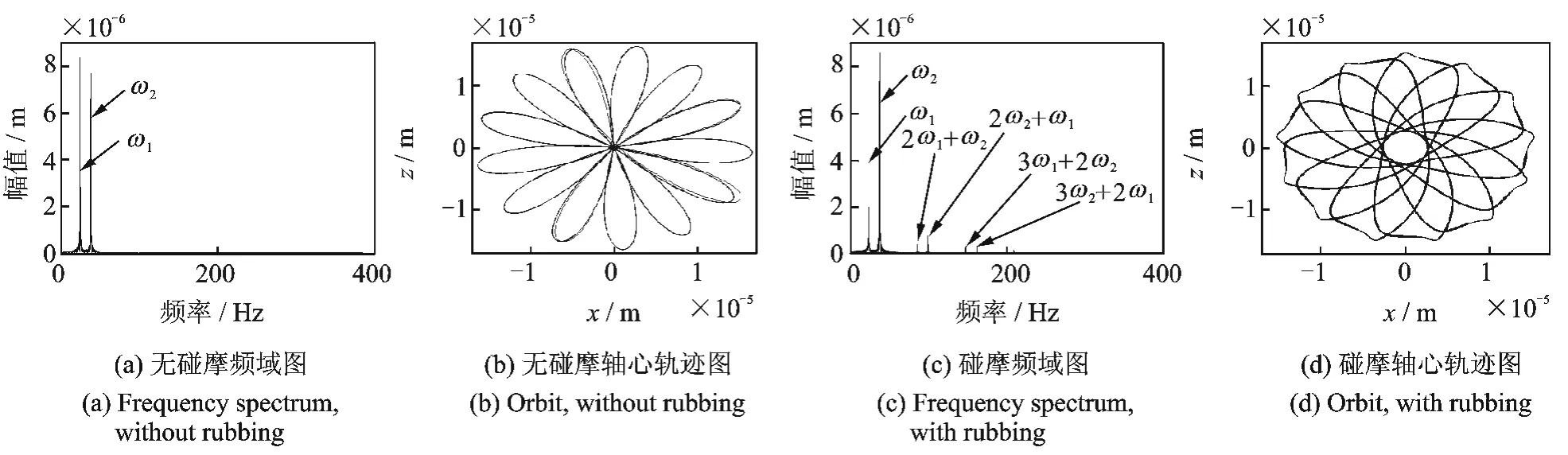
圖5 兩個一階臨界轉速之間系統無碰摩和碰摩時的頻譜圖和軸心軌跡圖Fig.5 Spectrum and orbit with and without rubbing between two first critical speeds of the system

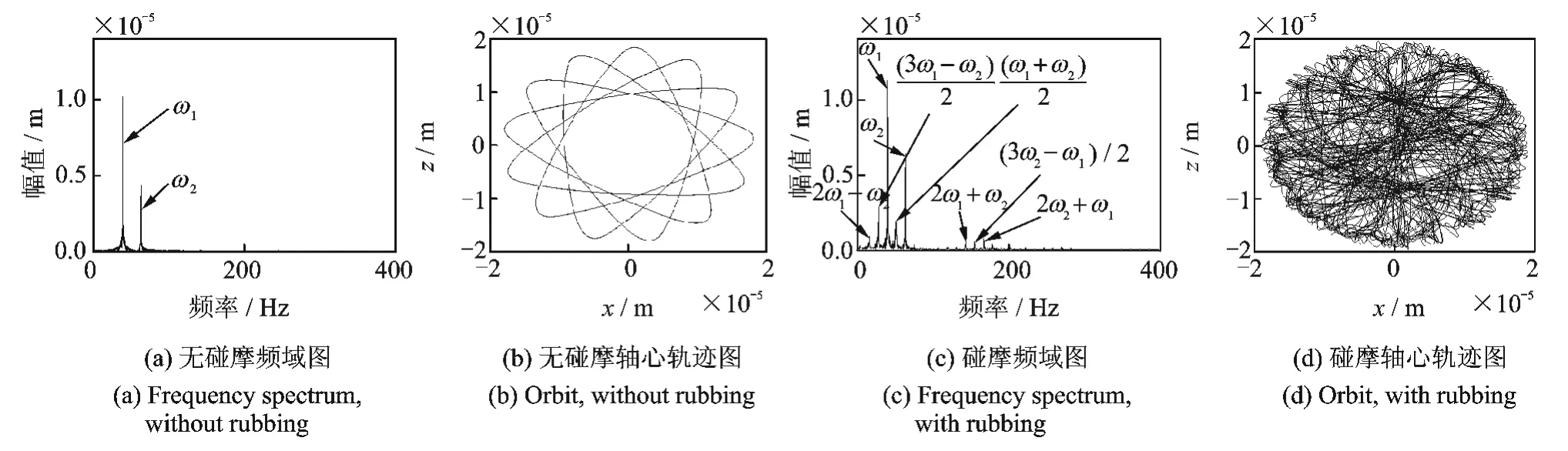
圖6 內轉子為主激勵的一階臨界轉速后系統無碰摩和碰摩時的頻譜圖和軸心軌跡圖Fig.6 Spectrum and orbit with and without rubbing after first critical speed excited by inner rotor

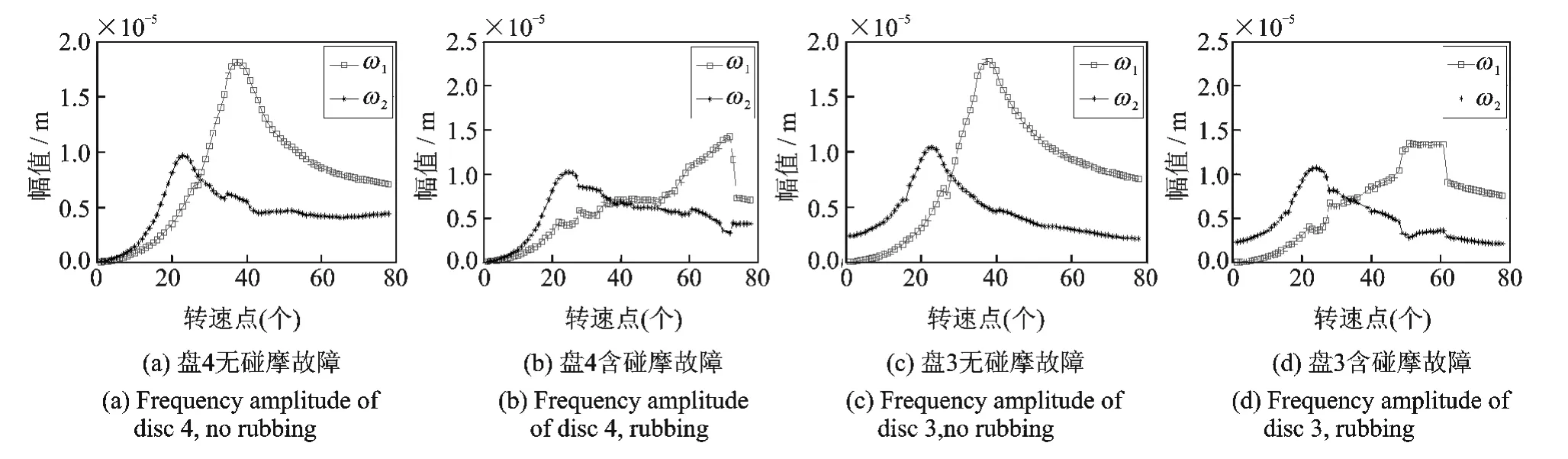
圖7 系統在無碰摩故障和有碰摩故障時的同步不平衡激勵頻率的幅值隨轉速變化圖Fig.7 Frequency amplitude of the synchronous unbalance response varies with speed for rubbing and no rubbing situation

由圖7可以看出：

1）無碰摩故障時，圖7（a）和圖7（b）中兩同步不平衡激勵頻率幅值在整個轉速范圍內先后出了一個峰值，分別對應以外轉子為主激勵的一階臨界轉速和以內轉子為主激勵的一階臨界轉速。較低的轉速時，外轉子同步不平衡激勵幅值大于內轉子同步不平衡激勵幅值，高速時則相反，二者的比例關系決定了轉子軸心軌跡的形狀。

2）由圖7中各圖對比可以看出，碰摩故障出現在系統響應幅值較大的轉速范圍內，與無碰摩時相比，該范圍內兩同步不平衡激勵幅值發生明顯變化。無論是外轉子（盤3）碰摩，還是內轉子（盤4）碰摩，ω1幅值變化程度遠較ω2幅值變化劇烈。分析原因：中介軸承的存在，使內外轉子之間的響應相互耦合；但由于內轉子剛度遠小于外轉子剛度，碰摩力對內轉子響應影響更大。

4 結 論

本文利用有限元方法，建立了含局部非線性的雙轉子系統的運動方程，采用自由界面模態綜合法對系統進行模態截斷，得到模態空間中的轉子系統運動方程，實現高維轉子系統維數的縮減。利用利用單自由度脈沖響應特性和Duhamel積分原理，完成了模態空間中轉子系統運動方程的數值求解。在此基礎上，開展了反向旋轉雙轉子系統碰摩故障響應特性研究。研究結論如下：

1）該方法將每一時間步長中，求解非線性方程組的維數限定為2倍的非線性力作用處的自由度個數，大大提高了計算效率。該方法僅利用自由狀態下的模態振型和模態頻率，考慮陀螺力矩和局部非線性作用力即可建立系統的動力學方程，為含局部非線性的雙轉子系統的動力特性分析提供了一種高效、便捷的方法；同時也為在系統材料參數未知的情況下，借助模態試驗建立系統動力學模型提供了一種有效的途徑。

2）外轉子為主激勵的一階臨界轉速前后，轉子碰摩時的軸心軌跡有明顯削峰和不規則碰摩特點；在一階臨界轉速后，碰摩故障使轉子軸心軌跡變得雜亂。

3）碰摩故障使系統響應的頻譜圖中出現了較豐富的頻率成分，除兩同步不平衡激勵頻率外，出現了二者的倍頻的組合頻率和組合頻率的分頻；在前兩種較低轉速情況下，系統的組合響應頻率均為兩同步不平衡響應頻率的倍頻和，在一階臨界轉速后，系統響應中出現了兩同步不平衡響應頻率的倍頻差及倍頻組合頻率的分頻。

4）碰摩故障對系統同步不平衡響應頻率幅值有著明顯的影響，由于內轉子剛度小，其同步響應頻率幅值變化更劇烈。

參考文獻：

［1］ 晏礪堂，王德友.航空雙轉子發動機動靜件碰摩振動特征研究［J］.航空動力學報，1998，13（2）：173—176.YAN Litang，WANG Deyou.Vibration features from rubbing between rotor and casing for a dual shaft aeroengine［J］.Journal of Aerospace Power，1998，13（2）：173—176.

［2］ 孟越，李其漢.應用整體傳遞系數法分析復雜轉子系統轉靜件碰摩振動特征［J］.航空動力學報，2003，18（1）：146—150.MENG Yue，LI Qihan.Using WTCM to analyze rub impact default of a complex rotor system［J］.Journal of Aerospace Power，2003，18（2）：146—150.

［3］ 單穎春，劉獻棟，何田，等.雙轉子系統碰摩有限元接觸分析模型及故障診斷［J］.航空動力學報，2005，20（5）：789—794.SHAN Yingchun，LIU Xiandong，HE Tian，et al.Research on the finite element impact－contact analytical model of dual－rotor system and its diagnosis method［J］.Journal of Aerospace Power，2005，20（5）：789—794.

［4］ 周海侖，陳果.航空發動機雙轉子－滾動軸承－機匣耦合系統動力學分析［J］.航空動力學報，2009，24（6）：1 284—1 291.ZHOU Hai－lun，CHEN Guo.Dynamic response analysis of coupling system dual rotor－ball bearing－stator for aero－engine［J］.Journal of Aerospace Power，2009，24（6）：1 284—1 291.

［5］ Han Qingkai，Luo Haitao，Wen Bangchun.Simulations of a dual－rotor system with local rub－impacts based on rigid－flexible multi－body model［J］.Key Engineering Materials，2009，413－414：677—682.

［6］ 袁惠群，賀威，韓清凱.發動機雙轉子－機匣耦合系統碰摩故障分析［J］.航空動力學報，2011，26（11）：2 401—2 408.YUAN Hui－qun，HE Wei，HAN Qing－kai.Analysis on rubs of double rotor－stator coupling system［J］.Journal of Aerospace Power，2011，26（11）：2 401—2 408.

［7］ 陳松霆，吳志強.反向旋轉雙轉子碰摩振動分析［J］.振動與沖擊，2012，31（23）：142—147.CHEN Song－ting，WU Zhi－qiang.Rubbing vibration analysis for a counter－rotating dual－rotor system［J］.Journal of Vibration and Shock，2012，31（23）：142—147.

［8］ Glasgow D A，Nelson H D.Stability analysis of rotorbearing systems using component mode synthesis［J］.Journal of Mechanical Design，Transactions of the ASME，1980，102（2）：352—359.

［9］ Li D F，Gunter E J.Component mode synthesis of large rotor systems［R］.American Society of Mechanical Engineers，n81－GT－147，1981.

［10］Li D F，Gunter E J.Study of the modal truncation error in the component mode analysis of a dual－rotor system［R］.American Society of Mechanical Engineers，n81－GT－144，1981.

［11］Wang W，Kirkhope J.Component mode synthesis for multi－shaft rotors with flexible inter－shaft bearings［J］.Journal of Sound and Vibration，1994，173（4）：537—555.

［12］鄧四二，賀鳳祥，楊海生，等.航空發動機雙轉子－滾動軸承耦合系統的動力特性分析［J］.航空動力學報，2010，25（10）：2 386—2 395.DENG Si－er，HE Feng－xiang，YANG Hai－sheng，et al.Analysis on dynamic characteristics of a dual rotorrolling bearing coupling system for aero－engine［J］.Journal of Aerospace Power，2010，25（10）：2 386—2 395.

［13］陳果.航空發動機整機振動耦合動力學模型及其驗證［J］.航空動力學報，2012，27（2）：241—254.CHEN Guo.A coupling dynamic model for whole aero－engine vibration and its verification［J］.Journal of Aerospace Power，2012，27（2）：241—254.

［14］Minh Hai Pham，Bonello Philip.An impulsive receptance technique for the time domain computation of the vibration of a whole aero－engine model with nonlinear bearings［J］.Journal of Sound and Vibration，2008，318（3）：592—605.

［15］Bonello Philip，Minh Hai Pham.A receptance harmonic balance technique for the computation of the vibration of a whole aero－engine model with nonlinear bearings［J］.Journal of Sound and Vibration，2009，324（1－2）：221—242.

［16］羅貴火，胡絢，楊喜關.反向旋轉雙轉子系統非線性特性分析［J］.振動工程學報，2009，22（3）：268—273.LUO Gui－huo，HU Xuan，YANG Xi－guan.Nonlinear dynamic performance analysis of counter－rotating dualrotor system［J］.Journal of Vibration Engineering，2009，22（3）：268—273.

［17］聞邦椿，顧家柳，夏松波，等.高等轉子動力學——理論、技術與應用［M］.北京：機械工業出版社，2000.

［18］楊喜關，羅貴火，唐振寰，等.高維反向旋轉雙轉子系統的建模方法及動力特性研究［J］.航空動力學報，2014，29（3）：585—595.