模糊C均值聚類與多相水平集圖割優(yōu)化相結(jié)合的圖像分割

宋 琳， 高滿屯， 王三民， 王淑俠

(西北工業(yè)大學機電學院，陜西 西安 710072)

模糊C均值聚類與多相水平集圖割優(yōu)化相結(jié)合的圖像分割

宋 琳， 高滿屯， 王三民， 王淑俠

(西北工業(yè)大學機電學院，陜西 西安 710072)

針對在分割多個目標時多相水平集模型對初始輪廓曲線敏感且計算量大的問題，提出采用模糊C均值聚類算法將圖像進行粗分割，初始化多相水平集函數(shù)，使用圖割算法分割出多相結(jié)果的方法。該方法能有效減小多相水平集算法對初始輪廓曲線的敏感性，使圖割算法在分割圖像時更容易分割出理想的目標輪廓；同時，采用圖割算法可使水平集函數(shù)很快收斂到能量最小值，有效減少計算量，提高計算效率。實驗表明該方法具有較好地分割效果和較高地分割效率。

模糊C均值聚類；圖像分割；圖割；多相水平集

圖像分割的目的是獲取輸入圖像中有意義的劃分，并且將其變成有限數(shù)量的不相交的同質(zhì)對象[1]。圖像分割的方法很多，其中最有效的方法就是以能量最小化問題來處理圖像分割問題，求解其最小極值。

求解最小極值一般采用兩種方法：一種方法是

列出相關(guān)聯(lián)的偏微分方程，計算偏微分方程的數(shù)值解；另一種方法是使用組合優(yōu)化工具求解相類似的離散問題的解。

近年來，偏微分方程的單相水平集方法[2]，在界面演化、圖像處理以及計算機視覺等領(lǐng)域得到了廣泛應用。但單相水平集模型假設圖像的目標區(qū)域和背景區(qū)域的灰度值近似為常量，所以，單相水平集模型適合分割灰度均勻、噪聲小、僅含有一個目標的圖像。使用單相水平集模型最終將圖像分割為目標與背景。

一個真實圖像往往存在兩個以上或更多的目標，為了實現(xiàn)多相分割，Vese和Chan[3]將水平集模型擴展成多相模型，即同時采用多個水平集函數(shù)分割圖像。通過多個水平集來表示多個區(qū)域(n個水平集函數(shù)最多可以表示“2n”個區(qū)域[4]，其中，n＞1)的多相分割算法。由于 C-V模型本身復雜的迭代算法，它的分割過程需要耗費大量的時間[5]。當采用多個水平集分割時，初始輪廓曲線的選擇直接決定算法的收斂與否，選擇不合適的初始輪廓曲線將導致算法最終不能收斂，從而大大降低了算法的穩(wěn)定性；即使算法最后能夠收斂，由于其各水平集之間缺乏從屬約束關(guān)系，在實際計算中會出現(xiàn)多個水平集收斂于同一目標的情況，大大降低了水平集的實際分割效率。

另外一個成功的圖像分割方法就是圖割[6]。圖割方法是一種快速計算的算法[7]。基于圖割方法可將圖像分割問題轉(zhuǎn)換為能量函數(shù)的優(yōu)化問題，通過合適的能量函數(shù)建立相應的網(wǎng)絡圖，利用最大流/最小割算法求解網(wǎng)絡圖最小割，從而獲取圖像分割的結(jié)果。圖割-最大流/最小割方法是一種全局優(yōu)化方法，通過解一系列二值分割問題來獲得多相目標[8-9]。因其高效性，近年來被廣泛應用于圖像分割領(lǐng)域中。

在圖像分割領(lǐng)域模糊 C均值聚類[10]方法是最普遍的數(shù)據(jù)聚類方法之一，其思想是使得被劃分到同一簇的對象之間相似度最高，而不同簇之間的相似度最低。模糊 C均值聚類方法允許輸入數(shù)據(jù)的噪聲和變化范圍相對大一些[11]。針對多相水平集和圖割方法的特點，本文提出了采用模糊 C均值聚類的多相水平集與多層圖割結(jié)合的圖像分割方法。該方法，不需要初始化，既能減少水平集計算量，又能提高分割計算效率，快速準確分割出多個目標。

1 相關(guān)背景

多相水平集的核心是建立一種定義在多個曲線上的能量函數(shù)，當能量函數(shù)收斂至極小值時，多個曲線剛好收斂至目標邊界。兩個水平集函數(shù)同時收斂可將圖像分割為4個目標區(qū)域如圖1所示，也就是說，兩個水平集函數(shù)可以找出4個目標邊界；同時，初始化曲線所包含的目標信息，決定著水平集函數(shù)的收斂結(jié)果。本文的兩個水平集是按兩層來排列的結(jié)構(gòu)。

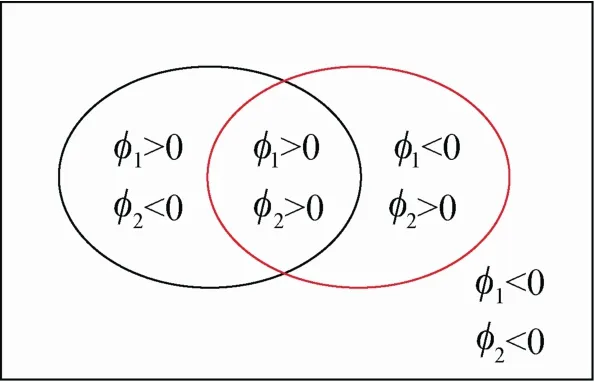
圖1 兩個水平集函數(shù)(φ1和φ2)代表兩個輪廓曲線

令 ?為 R2的有界開子集，φ1、φ2：?→R 的Lipschitz連續(xù)的水平集函數(shù)。p=(x,y)表示圖像中的任一像素點，兩個水平集函數(shù)φ1和φ2將定義域劃分成4個目標區(qū)域ω1, ω2, ω3和ω4，并且其中：

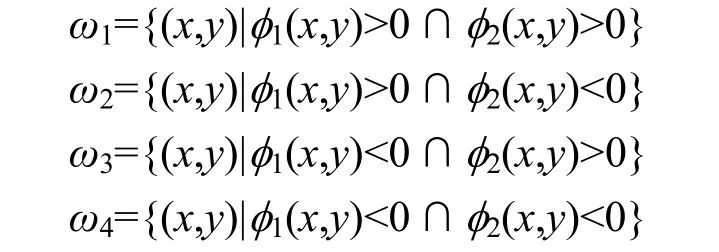
將零水平集曲線C定義為：

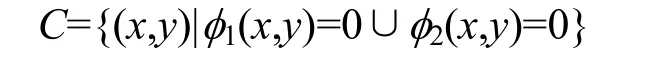
圖像分割的結(jié)果可通過求解式(1)能量函數(shù)最小值來獲得。

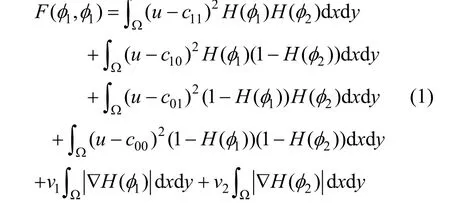
式中，ε為非負參數(shù)，當ε趨近于0時，式(2)接近于 H(φ)：

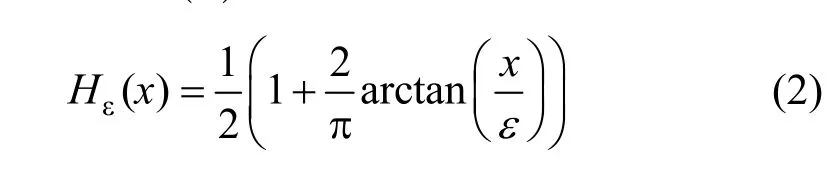
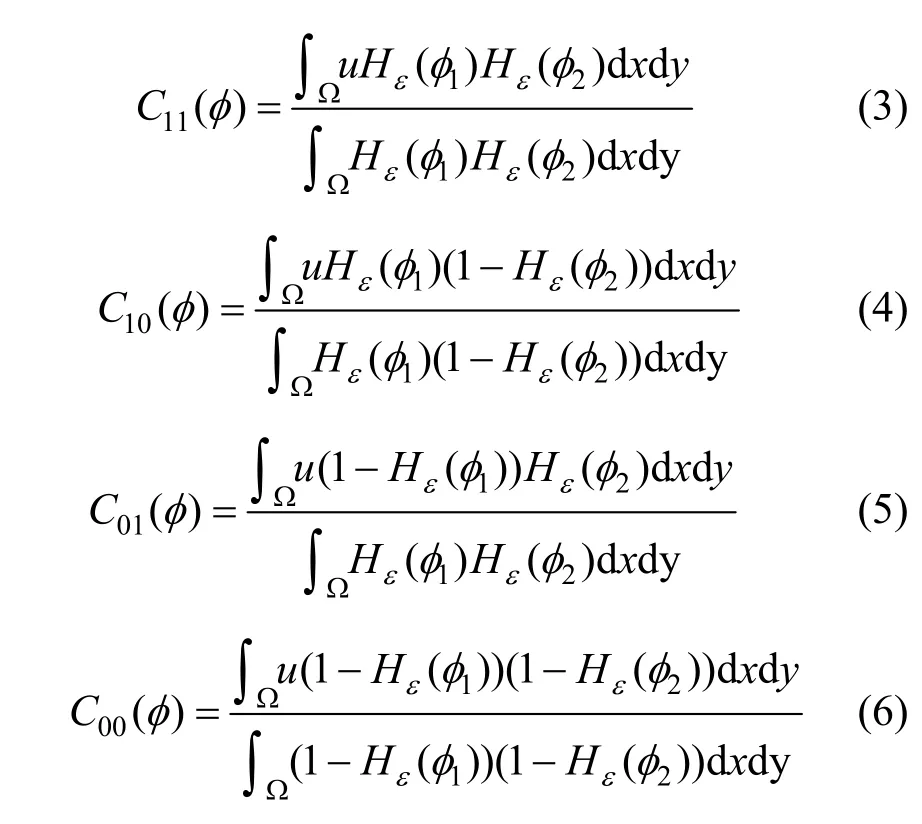
2 本文模型

多相水平集對于灰度均勻的圖像可以實現(xiàn)多目標分割，但對于灰度不均勻，噪聲較大的自然圖像，因多相水平集受初始輪廓曲線影響較大，分割結(jié)果不準確。多相水平集本身計算量大，計算效率低。因此，本文提出了采用模糊C均值聚類的多相水平集與多層圖割結(jié)合的圖像分割方法。

2.1 模糊C均值聚類初始化

模糊 C均值聚類方法通過計算每個數(shù)據(jù)樣本與聚類原型之間的隸屬度對圖像進行分割。假設樣本集合為T={ t1,t2,···,tn}，將其分成a個模糊組，并求每組的聚類中心mj(j=1,2,···,a)，使得非相似性指標的價值函數(shù)達到最小。該方法采用模糊劃分，將每個給定數(shù)據(jù)點用值在0,1間的隸屬度來確定其屬于各組的程度。

模糊C均值聚類方法的固有缺陷是：需要預先給定聚類個數(shù)；容易陷入局部極小值而得不到全局最優(yōu)解。因此，本文利用模糊C均值聚類方法將圖像粗略的劃分為a個部分，并聚類為預先設定的a個模糊組，初始化多相水平集函數(shù)，使用圖割算法，確定多相目標輪廓。

在本文中，以兩相水平集為例，預先給定的聚類個數(shù)為4，模糊C均值聚類將圖像粗分割成4個區(qū)域R1、R2、R3、R4，初始水平集函數(shù)可定義為：

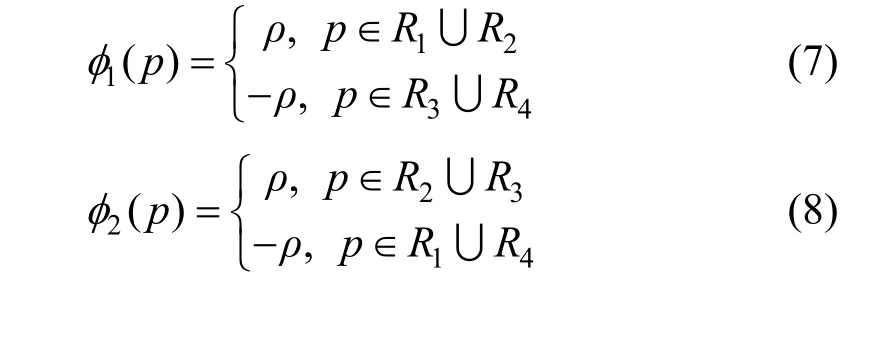
2.2 離散化能量泛函

本文采用圖割方法構(gòu)造能量函數(shù)，即以能量最小化模型構(gòu)造能量函數(shù)，從而將視覺問題轉(zhuǎn)化為能量函數(shù)最小化問題。利用圖割方法構(gòu)造兩相水平集能量函數(shù)，首先將兩相水平集泛函離散化表示。

將圖割方法引入兩相水平集模型，需要根據(jù)圖像構(gòu)造網(wǎng)絡，對于每一個像素點p∈Ω，(離散像素點集合)都有一個二進制變量組成的矢量與之對應，每一個像素點p對應著圖割網(wǎng)絡的一個節(jié)點，Xp所對應的節(jié)點是圖像像素點的兩倍，即構(gòu)造一個兩層網(wǎng)絡xp、yp，xp、yp的定義如下：

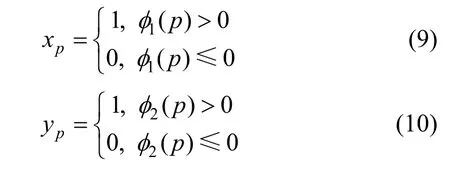
在離散優(yōu)化領(lǐng)域中，多相問題被稱為多標記問題，是將圖像區(qū)域中的每個像素點賦予的標記值的分配問題[12]。因此，Xp∈ {[1 1],[0 1],[1 0],[0 0]}。在兩相水平集模型中的 4個目標區(qū)域 ω1, ω2, ω3, ω4，分別對應4個標記值11，01，10和00。

能量函數(shù)的離散公式可表示為：

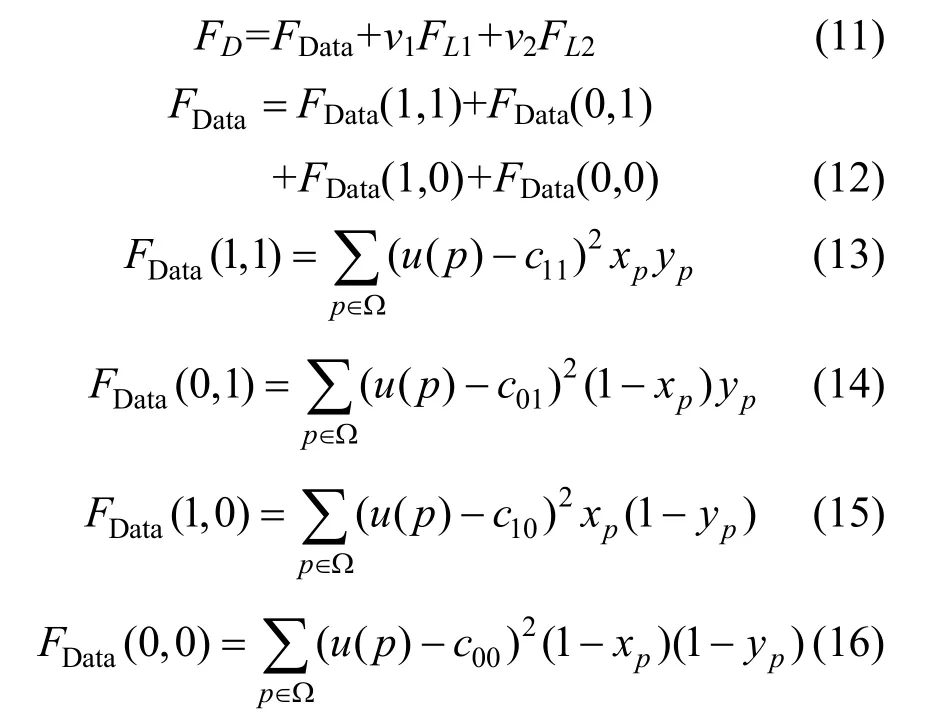
式中，p=(x,y)表示任一層中的圖像像素點，u （p）是p點的圖像灰度值， N(p)是p點的鄰域集合， wpq是邊 vpvq的權(quán)值。

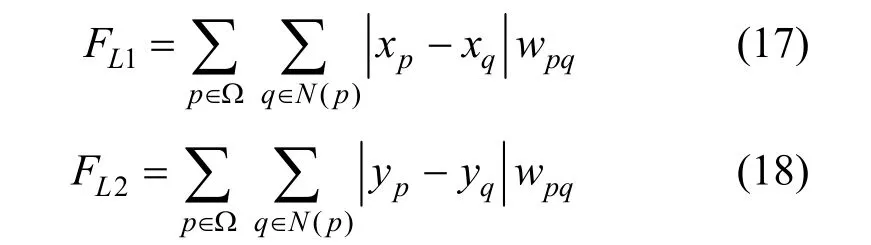
平均灰度值可表示為：

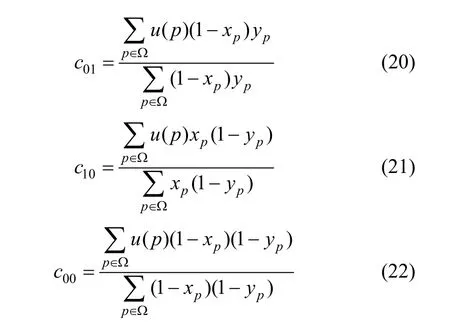
通過探索能量函數(shù)的最小能量值，來獲得分割結(jié)果圖像，其結(jié)果圖像是具有光滑輪廓的分段常數(shù)區(qū)域[13]。分段常數(shù)模型可近似為：

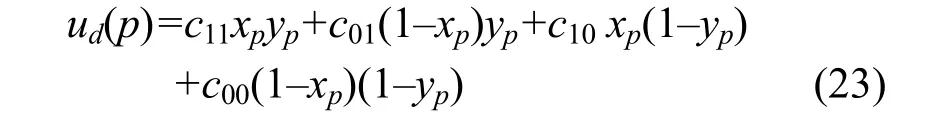
2.3 能量泛函最優(yōu)解

圖割方法根據(jù)圖像所構(gòu)造的網(wǎng)絡，使得能量與網(wǎng)絡割相對應，從而將能量最小化問題轉(zhuǎn)化為網(wǎng)絡最小割問題。根據(jù)最大流/最小割定理，將網(wǎng)絡最小割問題轉(zhuǎn)化為最大流問題。通過求解最大流問題，求得圖的最小割，從而獲得視覺問題的解。

利用圖割方法找到圖像對應的能量模型的最小割，計算出最小能量結(jié)果，最終生成多個目標區(qū)域的輪廓曲線。圖割方法的網(wǎng)絡節(jié)點(像素點)是按兩層來排列的，層內(nèi)節(jié)點之間的關(guān)系、層間節(jié)點之間的關(guān)系以及各節(jié)點與源、匯點的關(guān)系見圖 2～4。因此，為求得式(11)的最優(yōu)解，構(gòu)建的 3個圖分別代表 FL1、FL2、FData。G 代表離散能量函數(shù)FD。

利用圖割方法解能量泛函的最優(yōu)解，層內(nèi)像素點間的關(guān)系(邊)的權(quán)值，層間像素點間的關(guān)系(邊)和各像素點與源、匯點的關(guān)系(邊)的權(quán)值按如下方法確定。

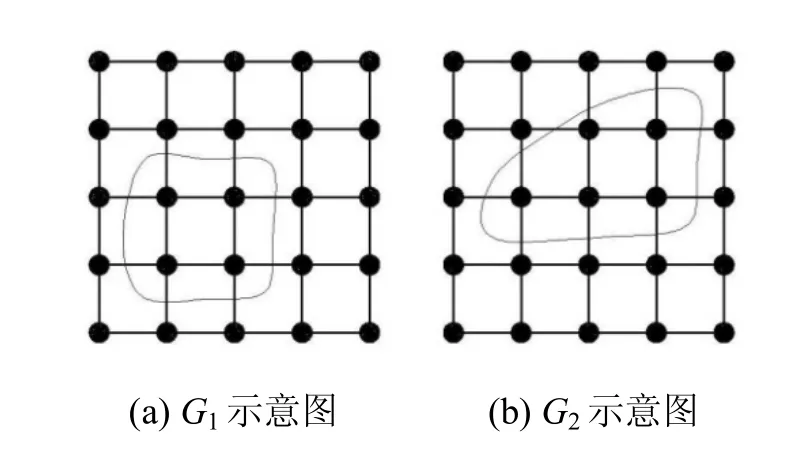
圖2 G1、G2示意圖

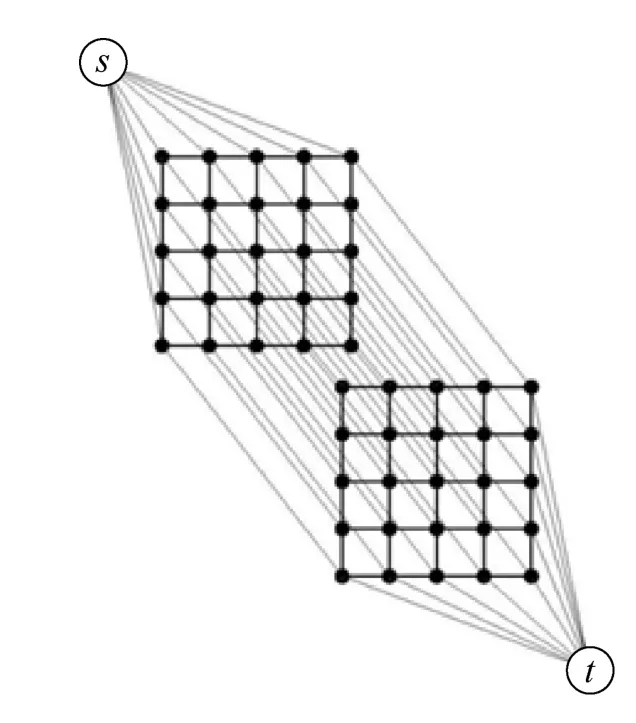
圖3 G3示意圖

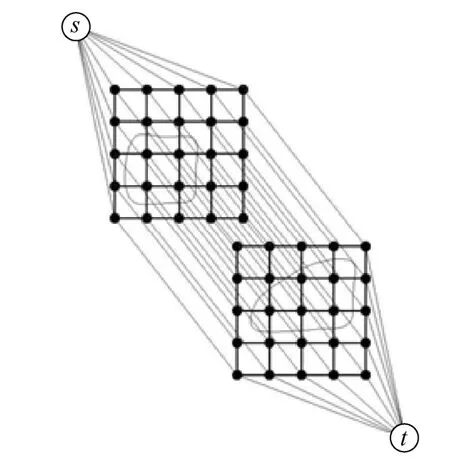
圖4 分割結(jié)果，G示意圖

每一個像素點p對應圖G2中的一個節(jié)點zp,p點的8鄰域集合為N(p)。當q∈N(p)，則有邊ezpzq的權(quán)值為wzpzq。

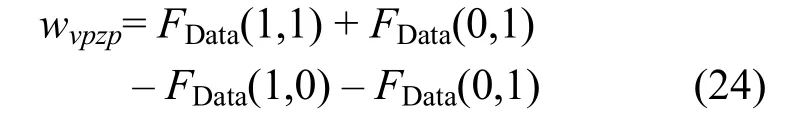
S點(源點)到節(jié)點vp的邊Svp的權(quán)值為wSvp：

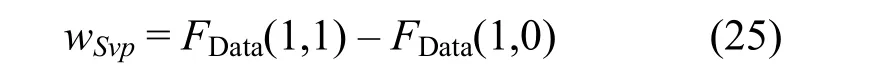
節(jié)點zp到T點(匯點)的邊zpT的權(quán)值wzpT：

本文的計算方法如下：

(1) 用模糊C均值聚類算法將圖像聚類，并進行初始化，構(gòu)造xp和yp。

(2) 計算c11, c10, c01, c00。

(3) 計算權(quán)值wvpvq, wzpzq, wvpzp, wSvp和wzpT。

(4) 計算能量函數(shù)值FD。

(5) 利用圖割算法解出圖G(圖4)的最小割，同時更新xp和yp。

(6) 將xp和yp組合出的4個區(qū)域標記為l1, l2, l3, l4。

(7) 重新計算c11, c10, c01, c00；回到第(3)步；直

到循環(huán)結(jié)束。

3 實驗結(jié)果分析比較

圖割算法的計算效率高；但基于梯度下降法的多相水平集，很容易得到局部極小，要獲得滿意的分割結(jié)果，算法的初始化很重要[14]，合適的初始位置才能分割出理想的多相結(jié)果。本文采用的自然圖像來自Berkeley數(shù)據(jù)庫。

圖 5(a)是采用手動方法初始化多相水平集函數(shù)，圖5(b)是經(jīng)過200次迭代計算后得到的分割結(jié)果。有的初始化曲線，使得算法不收斂，降低了算法的穩(wěn)定性，這里不再贅述。總之使用多相水平集算法，計算量大，且效率低，要得到滿意的分割結(jié)果需要耗費大量的時間去尋找最佳初始化曲線。

圖5 多相水平集方法分割圖像

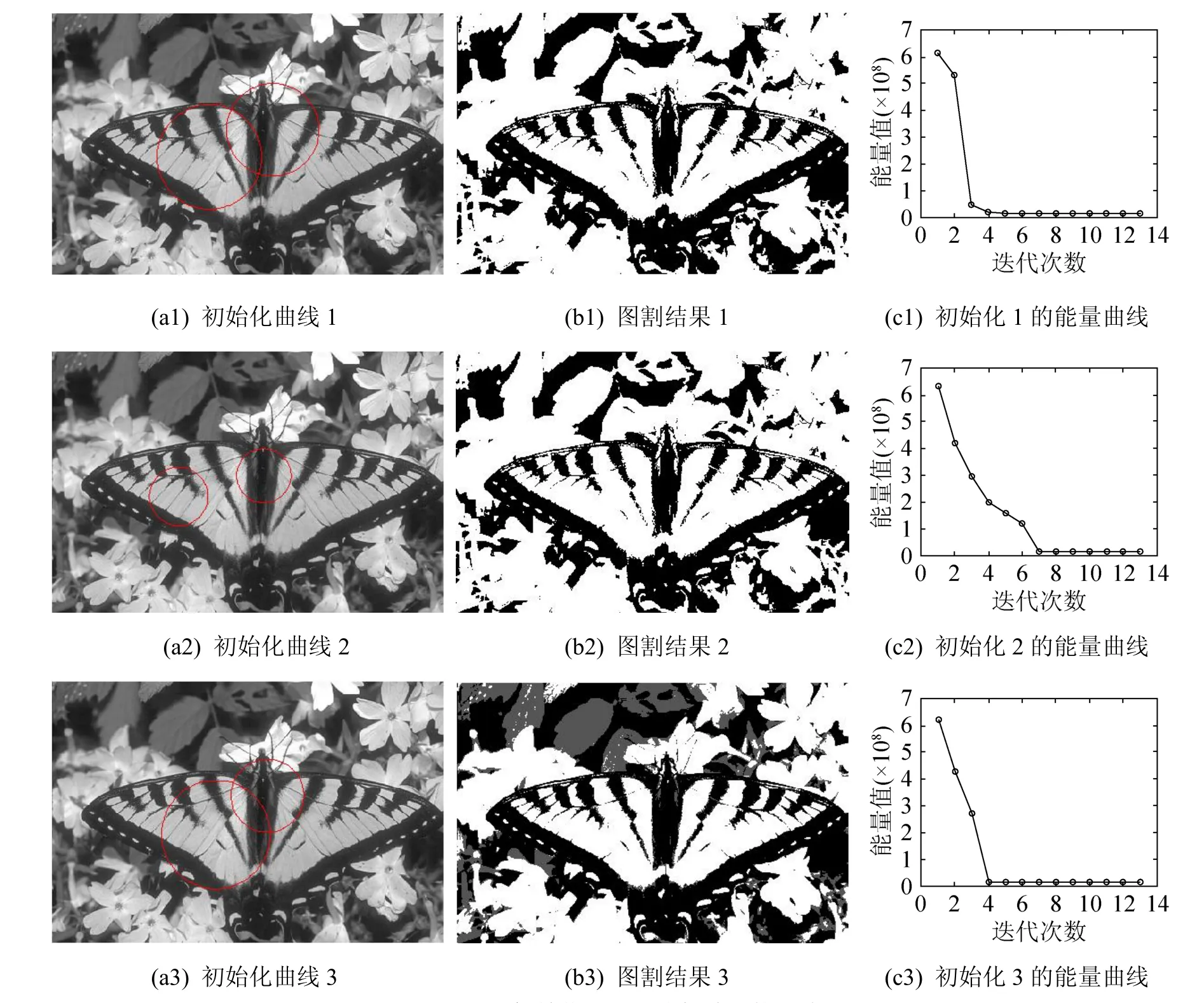
圖6 不同初始化位置對分割結(jié)果的影響

圖 6(a1)～(a3)是采用手動初始化多相水平集函數(shù)的方法，圖 6(b1)～(b3)是經(jīng)過使用圖割算法對圖像進行多相分割得到的結(jié)果。

圖 6(a1)～(a3)中的圓圈線是多相水平集的初始化曲線；圖 6(b1)～(b3)是分割出的多相結(jié)果用不同灰度填充后的效果；圖 6(c1)～(c3)是三次分割的能量值曲線。從分割結(jié)果可以看出，分割結(jié)果對初始化非常敏感，圖6(a1)和(a2)的初始化都只分割出兩相結(jié)果，只有圖6(a3)的初始化得到了三相結(jié)果。在實際計算中，滿意地分割結(jié)果，往往伴隨著很多次初始化之后才能得到。由于圖割算法的使用，三次分割的能量值很快收斂到最小，計算效率很高。

模糊C均值聚類能快速將圖像進行粗分割，本文的算法就是采用模糊 C均值聚類初始化水平集函數(shù)，使用圖割算法對圖像進行多相分割。

以下采用本文的算法將圖像分割為多相結(jié)果，

并予以說明分析。

圖7是要被分割的自然圖像。圖8是采用模糊C均值聚類將圖像聚類后，來構(gòu)造的像素點Xp，紅色和青色區(qū)域是構(gòu)造的初始化像素點xp、yp中的目標相。初始化是圖像分割的第一步，由于模糊C均值聚類已經(jīng)將圖像進行聚類，因此兩相水平集函數(shù)的初始化輪廓曲線就是對圖像進行了粗分割的結(jié)果。圖像中待分割的目標與背景信息已經(jīng)粗略形成，再者，兩層水平集之間又有著聯(lián)系和約束關(guān)系，目標就會更容易被分割出來。因此，模糊C均值聚類初始化水平集輪廓曲線有利于多相分割結(jié)果的形成，使得多相分割結(jié)果對初始化的敏感性大大降低，從而提高了算法的穩(wěn)定性。

圖7 原始圖像

圖8 用模糊C粗分割圖像

圖 9是采用圖割算法迭代后的分割結(jié)果矢量Xp，紅色和黃色區(qū)域是結(jié)果變量xp、yp中的目標相。圖 10是采用本算法的圖像分割結(jié)果，使用不同灰度來填充分割出的多個區(qū)域面積。

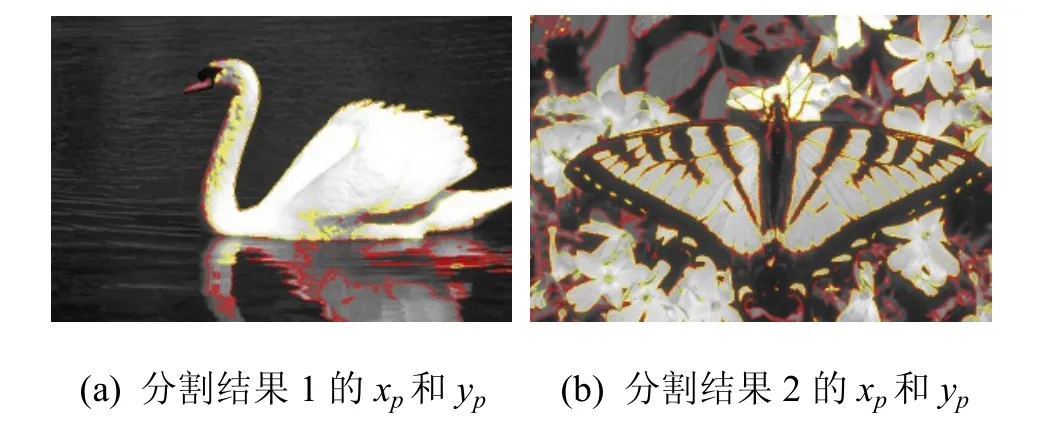
圖9 使用本文算法的xp和yp結(jié)果

從圖7～10可以看出，采用模糊C均值聚類粗分割的圖像，噪聲比較大，初始化的輪廓曲線還有噪聲的干擾。使用多相水平集圖割算法迭代后，噪聲被去掉，圖像中目標的邊界被快速準確的分割出來。

模糊 C均值聚類只能將圖像聚類為預設定的幾個部分，邊緣比較模糊，這是由于模糊C均值聚類對噪聲比較敏感，當灰度值相近時，圖像內(nèi)的目標不能被完全分割。圖割方法有著全局最優(yōu)性和分割結(jié)果的強魯棒性，快速確定目標個數(shù)，使圖像中的目標相很快被分割，水平集函數(shù)的能量值迅速收斂，達到最小。

圖10 分割結(jié)果

從圖11的能量值得出曲線看，水平集圖割算法在3～4次迭代就可以使得能量值收斂到最小，得到滿意的分割結(jié)果，計算效率很高，計算量大幅度降低。

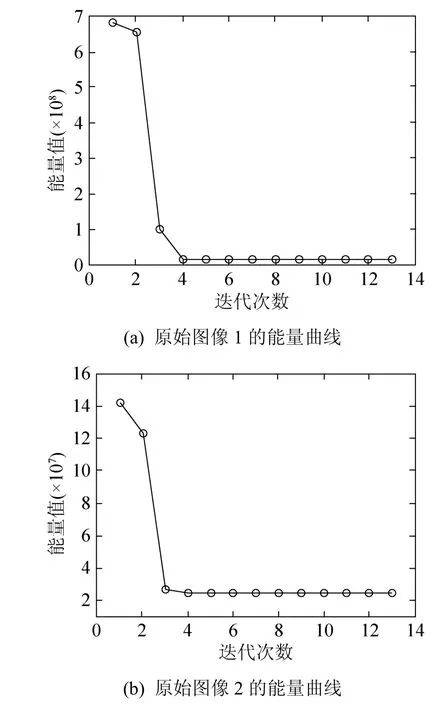
圖11 能量值曲線

圖 12是采用本文算法對自然圖像分割的又一個實例，圖12(a)是原始圖像；圖12(b)是采用模糊C均值聚類對離散水平集函數(shù)進行了初始化，這樣的初始化使得圖像的兩個層的目標信息相對明確；

圖12 分割圖像實例

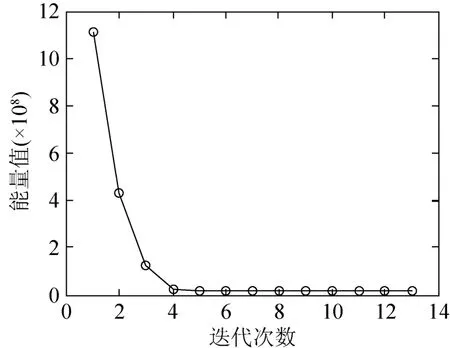
圖13 實例的能量值曲線

4 結(jié) 論

本文提出了采用模糊 C均值聚類初始化兩相水平集函數(shù)的圖割算法。該模型可以有效減小多相水平集函數(shù)對初始輪廓曲線的敏感性，增強了水平集算法的穩(wěn)定性，初始化使得圖像分割的目標相與噪聲相對明晰，更容易分割出目標相；采用圖割算法進行優(yōu)化，能量值很快收斂至最小，有效減少計算量，提高計算效率。

[1] Moreno J C, Surya P V B, Proen?a H, et al. Fast and globally convex multiphase active contours for brain MRI segmentation [J]. Computer Vision and Image Understanding, 2014, 125(2)： 237-250.

[2] Osher S, Sethian J A. Fronts propagating with curvature dependent speed： algorithms based on Hamilton-Jacobi formulation [J]. Journal of Computational Physics, 1988, 79(1)： 12-49.

[3] Vese L A, Chan T F. A multiphase level set framework for image segmentation using the Mumford and Shah model [J]. International Journal of Computer Vision, 2002, 50(3)： 271-293.

[4] Bogovic J A, Prince J L, Bazin P L. A multiple object geometric deformable model for image segmentation [J]. Computer Vision and Image Understanding, 2013, 117(2)：145-157.

[5] Zhao Minrong, Zhang Xiwen, Jiang Juanna. Topography image segmentation based on improved Chan-Vese model [J]. Computer Aided Drafting, Design and Manufacturing, 2013, 23(2)：13-16.

[6] Boykov Y, Veksler O, Zabih R. Fast approximate energy minimization via graph cuts [J]. IEEE Transactios on Pattern Analysis and Machine Intelligence, 2001, 23：1222-1239.

[7] Kolmogorov V, Zabih R. What energy functions can be minimized via graph cuts? [J]. IEEE Transactios on Pattern Analysis and Machine Intelligence, 2004, 26(2)：147-159.

[8] Boykov Y, Funka-Lea G. Graph cuts and efficient N-D image segmentation [J]. International Journal of Computer Vision, 2006, 70(2)： 109-131.

[9] Zeng Yun, Samaras D, Chen Wei, et al. Topology cuts： a novel min-cut/maxflow algorithm for topology preserving segmentation in ND images [J]. Computer Vision and Image Understanding, 2008, 112(1)： 81-90.

[10] Pal N R, Pal K, Keller J M, et al. A possibilistic fuzzy c-means clustering algorithm [J]. IEEE Transactions on Fuzzy Systems, 2005, 13(4)： 517-530.

[11] Wang Zhimin, Song Qing, Soh Y C, et al. An adaptive spatial information-theoretic fuzzy clustering algorithm for image segmentation [J]. Computer Vision and Image Understanding, 2013, 117(10)： 1412-1420.

[12] Bae E, Jing Yuan, Tai Xuecheng. Global minimization for continuous multiphase partitioning problems using a dual approach [J]. International Journal of Computer Vision, 2011, 92(1)： 112-129.

[13] Sashida S, Okabe Y, Lee H K. Comparison of multi-label graph cuts method and Monte Carlo simulation with block-spin transformation for the piecewise constant Mumford-Shah segmentation model [J]. Computer Vision and Image Understanding, 2014, 119(1)： 15-26.

[14] Brown E S, Chan T F, Bresson X. Completely convex formulation of the Chan-Vese image segmentation model [J]. International Journal of Computer Vision, 2012, 98(1)： 103-121.

An Image Segmentation Method by Combining Fuzzy C-Means Clustering with Graph Cuts Optimization for Multiphase Level Set Algorithms

Song Lin, Gao Mantun, Wang Sanmin, Wang Shuxia
(School of Mechanical Engineering, Northwestern Polytechnical University, Xi?an Shaanxi 710072, China)

Multiphase level set model is sensitive to initial contour curve and has huge computation in the process of the multiple objects? segmentation. A novel Image segmentation method is presented for multiphase scenario, which initializes the multiphase level set function by coarse image segmentation using fuzzy C-means clustering algorithm and applies graph cuts algorithm to acquire multiphase output image. The method can effectively reduce the sensitivity of the multiphase level set algorithm to initial contour and is easier to gain the multiphase output image by graph cuts algorithm. At the same time, the multiphase level set function quickly converge to the minimum energy value with small amount of calculation and high computational efficiency using the graph cuts algorithm. The experiments show that this method has better segmentation effect and higher efficiency of image segmentation.

fuzzy C-means clustering; image segmentation; graph cuts; multiphase level set

TP 391

A

2095-302X(2015)04-0563-07

2014-12-11；定稿日期：2015-02-11

國家自然科學基金資助項目(51105310)

宋 琳(1975–)，女，河北任縣人，講師，博士研究生。主要研究方向為計算機視覺和模式識別。E-mail：songlim03@sina.com