自適應收縮函數的Contourlet變換圖像去噪方法

牛為華， 孟建良， 王 澤， 崔克彬

(華北電力大學控制與計算機工程學院，河北 保定 071003)

自適應收縮函數的Contourlet變換圖像去噪方法

牛為華， 孟建良， 王 澤， 崔克彬

(華北電力大學控制與計算機工程學院，河北 保定 071003)

針對傳統圖像在去噪過程中存在丟失細節且去噪效果不理想的情況，提出一種自適應收縮函數的Contourlet變換圖像去噪方法。該方法利用Contourlet變換的基本形式，結合軟閾值和硬閾值收縮函數的優點定義自適應收縮函數，并將其應用于圖像去噪。實驗結果表明，所提出的方法能有效消除噪點，圖像的峰值信噪比及增強因子等圖像質量指標有明顯地提高，去噪后圖像的視覺效果良好。

Contourlet變換；自適應收縮函數；收縮階數；軟閾值；硬閾值

圖像處理技術在人類生產和生活中起著重要作用。然而，由于受陰天、霧天、拍攝抖動等因素的干擾，使得圖像會受到多種噪聲污染，其噪聲信息會干擾后續圖像加工的結果，比如圖像的拼接、融合、識別等。因此，圖像去噪成為所有圖像處理的前提，而去噪的效果將直接影響后續圖像處理的結果。

傳統的圖像去噪方法主要有：空間域濾波和頻率域濾波。空間域濾波是針對像素點的灰度值，可進行直接運算或其他方式的處理，如基于偏微分方程的方法[1-2]、全變分[3]方法及BM3D[4-5]方法等。文獻[1]建立了加權混合噪聲模型的能量泛函表達式，利用變分法獲得其歐拉-拉格朗日方程并給出其顯式差分迭代求解算法，提高了模型數值算法的速度和穩定性，避免了降噪后圖像的階梯效應。文獻[3]將經典全變分模型與圖像平滑擴散

原理相結合，構造了新的擴散函數，能有效去除噪聲。但是，這些方法在處理圖像邊緣和細節上的像素效果較差，造成圖像模糊。文獻[4]所提出的BM3D方法利用圖像自身的相似性，通過對比圖像中不同位置小塊圖像之間的相似程度，來估計圖像像素原灰度值，從而還原圖像原始像素點的灰度值。BM3D去噪方法不僅視覺效果非常好，而且去噪后的圖像有很高的峰值信噪比(peak signal to noise ratio，PSNR)。該算法在處理圖像塊之間的相似性時，需要進行大量的相似性比較，造成該算法的執行效率稍差。變換域濾波先把圖像信息由空間域的像素點灰度值轉換成頻率域等其他域，然后通過目標域中所帶有的一些性質把轉換后的系數進行適當處理來達到弱噪目的，最后再經過逆變換還原圖像，如小波變換法[6-7]、稀疏表示方法[8-9]及 Contourlet變換法[10-12]等。小波理論已廣泛應用于圖像去噪中，由于常用的二維張量積小波具有各向同性且方向選擇性較差的特點，一般只適于刻畫圖像中點的奇異性，難以刻畫圖像中的邊緣和紋理等高維幾何特性，因而相繼出現了幾種超小波，如曲波[6]、輪廓波[7]等，這些方法在超小波去噪的同時較好地保留圖像中的線狀結構。文獻[8]利用圖像的非局部自相似性獲得原始圖像的稀疏編碼系數估計，然后將觀測圖像的稀疏編碼系數集中應用于這些估計，構造了NCSR模型，在圖像復原、去噪、去模糊等方面均取得了很好的效果。文獻[9]利用一種基于學習的框架進行圖像去模糊，該方法首先構建了耦合的學習字典，對訓練樣本應用耦合稀疏表示分析學習模型，由于這些字典的原子耦合在一起，重建信息可以在清晰與模糊圖像之間傳播；然后，在重建系數保持不變的情況下，利用清晰字典恢復最終結果，該方法可以處理未知模糊情形。

Contourlet變換作為一種新的多尺度變換，能在任意尺度上實現任意方向的分解，擅長描述圖像中的輪廓和方向性紋理信息。將小波變換與Contourlet變換相結合能最大限度實現二者的優勢互補，從而更好地實現圖像去噪。目前Contourlet變換在圖像去噪等領域有著較為廣泛地應用，但其缺乏平移不變性，在進行圖像處理時會在圖像邊緣處引起偽吉布斯失真[13]。文獻[14]研究了基于小波-Contourlet變換的硬閾值圖像去噪方法，解決了由小波-Contourlet變換平移變異性而產生的偽吉布斯現象，去噪效果得以加強；文獻[15]利用非抽樣Contourlet變換的多尺度、多方向性以及平移不變性，對加噪圖像進行非抽樣Contourlet變換，使得到的變換系數采用分層最佳軟閾值處理，再將其反變換實現圖像的去噪；文獻[16]利用改進閾值函數對閾值處理的 Contourlet變換的高頻細節系數上頻、中頻和下頻進行處理，較好地彌補了各種閾值函數的缺陷；文獻[17]根據Contourlet多尺度、多方向的特性，將軟、硬閾值函數相結合，根據不同尺度、不同方向選擇不同的閾值，保留了兩種閾值函數的優點；文獻[18]提出了基于分數階微積分的數字圖像去噪方法，在去噪的同時較好地保留圖像邊緣紋理細節信息。因此，本文將Contourlet變換中軟閾值與硬閾值的處理結合起來，構造了新的收縮函數，通過實驗對比分析了軟、硬閾值方法、改進的Contourlet變換法、分數階圖像去噪方法以及BM3D方法，并對實驗結果從定性和定量兩個方面進行了分析。

1 Contourlet變換

Contourlet變換是一種“真正”的圖像二維表示方法，它不僅繼承了小波變換的多分辨率時頻分析特征，而且擁有良好的各向異性，能用比小波變換更少的系數來表達光滑的曲線，并更好地捕獲圖像的邊緣和輪廓信息。Contourlet變換將多尺度分析和多方向分析分開進行，首先由拉普拉斯金字塔(Laplacian pyramid，LP)變換對圖像進行多尺度分解以捕獲奇異點，接著由方向濾波器組(directional filter bank，DFB)[19]，將分布在同方向的奇異點合成為一個系數，再用類似于輪廓段的基結構逼近原圖像，Contourlet分解過程如圖1。

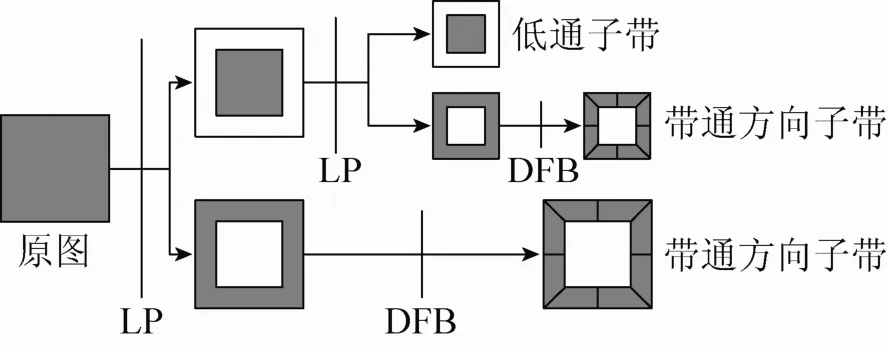
圖1 Contourlet分解的過程

(1) LP濾波器。Laplacian塔式分解算法通過對信號分辨率進行改變，對于相關圖像細節根據特定的目標來處理。在塔式分解中，先通過相關處理獲得低頻圖像，采用低通濾波器對上一尺度低頻圖像進行濾波，再進行下采樣操作。上采樣

操作應用于低頻圖像后，使用高通濾波器對得到的結果進行高通濾波，并與低頻圖像差分，得到LP分解的高頻部分，其分解過程如圖2所示[20]。

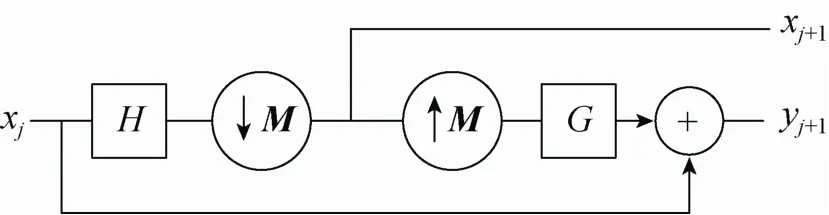
圖2 塔式分解過程[20]

其中， xj為第j尺度上的低頻圖像，H為低通濾波器，G為合成濾波器，M為采樣矩陣且。LP分解對源圖像 xj抽樣后做低通濾波，得到源圖像的一個平滑概貌部分 xj+1。源圖像與 xj+1的差值 yj+1相當于一個帶通圖像，對概貌xj+1重復進行該操作，使源圖像不斷被分解，得到一個塔狀結構，稱為Laplacian金字塔。

(2) 迭代方向濾波器組。其由扇形濾波器組級聯構成，二維雙通道扇形濾波器組通過梅花形采樣與扇形濾波器相結合而構成，圖 3是雙通道扇形濾波器組原理圖[21]。

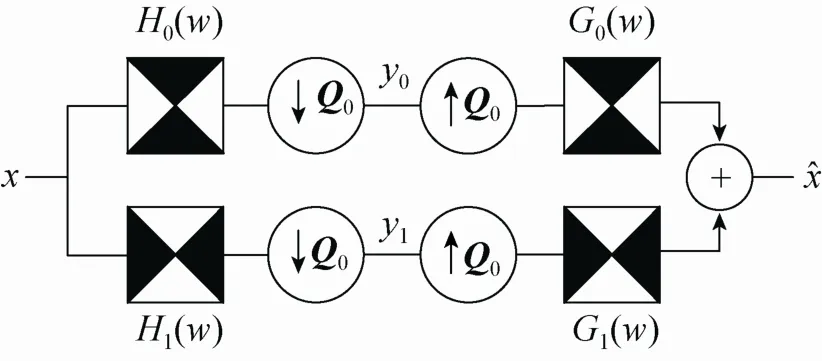
圖3 分解和重構原理圖[21]

2 自適應收縮函數Contourlet變換

2.1 軟、硬閾值函數

Dohono的小波閾值去噪方法簡潔、方便、視覺效果較好，從最小均方誤差角度看是有效的。主要依據為：整個小波域內分布著噪聲的能量，而對于小波域內屬于 Besov空間的信號來說，其能量主要集中在幾個系數中，所以經過小波分解操作，噪聲的系數會小于信號系數，可以設置一個合適閾值K，對于小于K的系數，置零并舍棄，此時系數中占主導地位的是噪聲；對于大于K的系數，按某一固定量向零收縮(軟閾值方法)或者直接保留下來(硬閾值方法)，這時系數中占主導地位的是信號，最后進行小波重構得到去噪后的結果。

圖像的高頻信息主要集中在某些紋理的法線、輪廓和邊緣上，體現著圖像的細節，因此圖像的高頻信息存在于這3個方向上的細節系數中，其圖像也具有明暗變化較大的特點。噪聲是隨機產生的，高頻信息中也經常含有噪聲，噪聲對應的小波系數一般較小，僅由部分細節系數描述。適當尺度地將噪聲與信號進行分解后，就可以將二者有效分離。

去噪的關鍵是修改細節系數，圖像最終效果的質量也由此決定。軟、硬閾值是最常用的兩種方法。

(1) 收縮函數中硬閾值數學表達式為：

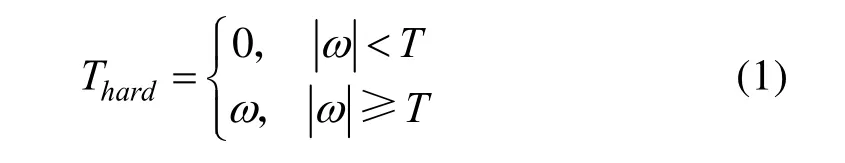
其中，ω表示含噪圖像的小波系數，T表示閾值，Thard表示硬閾值收縮函數。其目的是將大于或等于閾值的系數保留并去掉幅值較小的系數(通常噪聲的小波系數比較小)，小波系數的估計在硬閾值濾波中是無偏的，缺點是濾波后可能會產生突變，尤其是在圖像的邊緣處。

(2) 收縮函數中軟閾值數學表達式為：

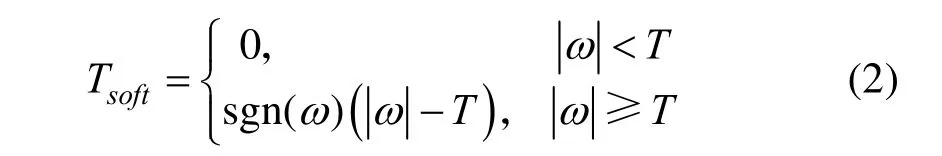
其中，sgn代表符號函數。軟閾值為使小波域內的系數連續，小波系數大于閾值時，對其進行收縮操作后保存下來。因為整個過程中剪掉了一部分幅值，而且系數的估計是有偏的，所以濾波后圖像的缺點是過于平滑。

2.2 自適應收縮函數

為了兼顧兩種收縮方式優點，對收縮函數進行重新構建。

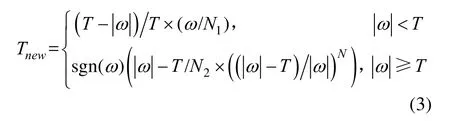
其中，N1，N2取正整數，N取大于等于0的整數。

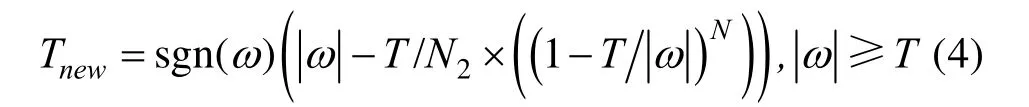
對于式(3)，分解后系數本身以及 N1，N2及N的選取如下：

以上分析說明，無論是通過分解系數本身還是階數的選取，由于收縮因子與階數的共同作用，可以使改進后的收縮函數在軟、硬閾值間靈活調整，可增強去噪過程的適應能力，且對未考慮的軟、硬閾值收縮函數也考慮了進去，進一步提高了函數的效果。

2.3 算法步驟

將新的收縮函數應用于Contourlet閾值去噪，算法步驟如下：

(1) 將原始圖像加噪；

(2) 對含噪圖像進行Contourlet分解，建立細節分量圖像序列；

(3) 設置閾值；(4) 依據式(3)處理各層分解的細節分量系數；(5) 將處理后的系數進行Contourlet逆變換，獲得重建圖像。

3 實驗結果

式(3)中，由于系數 N1， N2及收縮階數N可變，故采用不同的系數對圖像進行處理并選取適宜的去噪效果系數。為了驗證該方法的優越性，對增加高斯白噪聲 σ= 25的圖像進行去噪，分析比較了硬閾值去噪、軟閾值去噪、文獻[16]方法、文獻[17]方法及分數階方法(取文獻[9]中最好的階次v =-0 .8)。同時，為了保證實驗結果的一致性，選用了512× 512的標準測試圖像；采用文獻[4]的高斯白噪聲添加方法；Contourlet變換選擇“9-7”塔式分解和“pkva”方向濾波器組進行的總分解層數為3，方向數分別為4、8、16。實驗結果如圖4～6所示。

由圖 4～6可以看出，應用硬閾值和軟閾值的Contourlet變換對圖像有一定的去噪作用，但也造成了圖像的細節信息丟失，以至于圖像出現了模糊現象；分數階方法對于圖像的去噪有一定效果，且對比度以及細節信息的凸顯都有顯著地提高，但對于灰度變化較大的區域出現了高頻信息的過度銳化，導致噪點清除的不理想；文獻[16]和文獻[17]方法去噪效果較好，但文獻[17]方法會出現局部階梯效應；應用本文方法對圖像的噪點清除較明顯，細節信息突出，紋理較清晰。實驗結果表明，收縮函數系數 N1=7，N2=6，收縮階數 N =5時，去噪效果較好，因此在算法的實際應用中，可以根據圖像去噪程度來適當選取參數，從而實現圖像的自適應收縮函數的Contourlet變換去噪。

圖4 不同方法去噪后的peppers圖像

圖5 不同方法去噪后的lena圖像

圖6 不同方法去噪后的boat圖像

4 圖像去噪質量評價

圖像去噪的質量可從定性和定量兩方面進行評價。定性評價需依靠圖像的視覺效果進行評價，如圖7～9。而定量方法的評價目前并沒有統一的標準。本文選用了反映圖像灰度值變化的圖像灰度值在x方向上的投影分析方法、反映圖像細節信息的參數峰值信噪比(peak signal to noise ratio，PSNR)、均方根誤差(mean squared error，MSE)和圖像增強因子(image enhancement factor，IEF)對去噪后的圖像進行綜合評價[22]。

4.1 圖像灰度值投影分析比較

對圖4～6中去噪后的圖像灰度值作縱向(x方向)投影進行對比分析，投影結果如圖7～9所示。

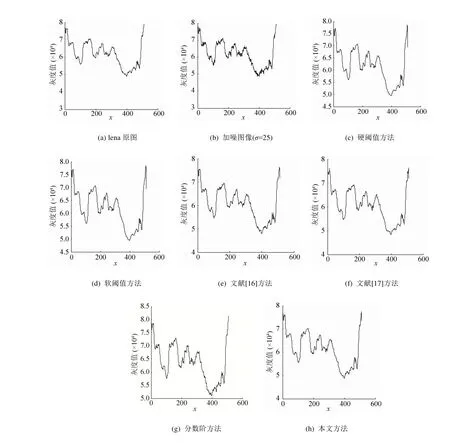
圖7 圖4中各圖的灰度值在x方向投影

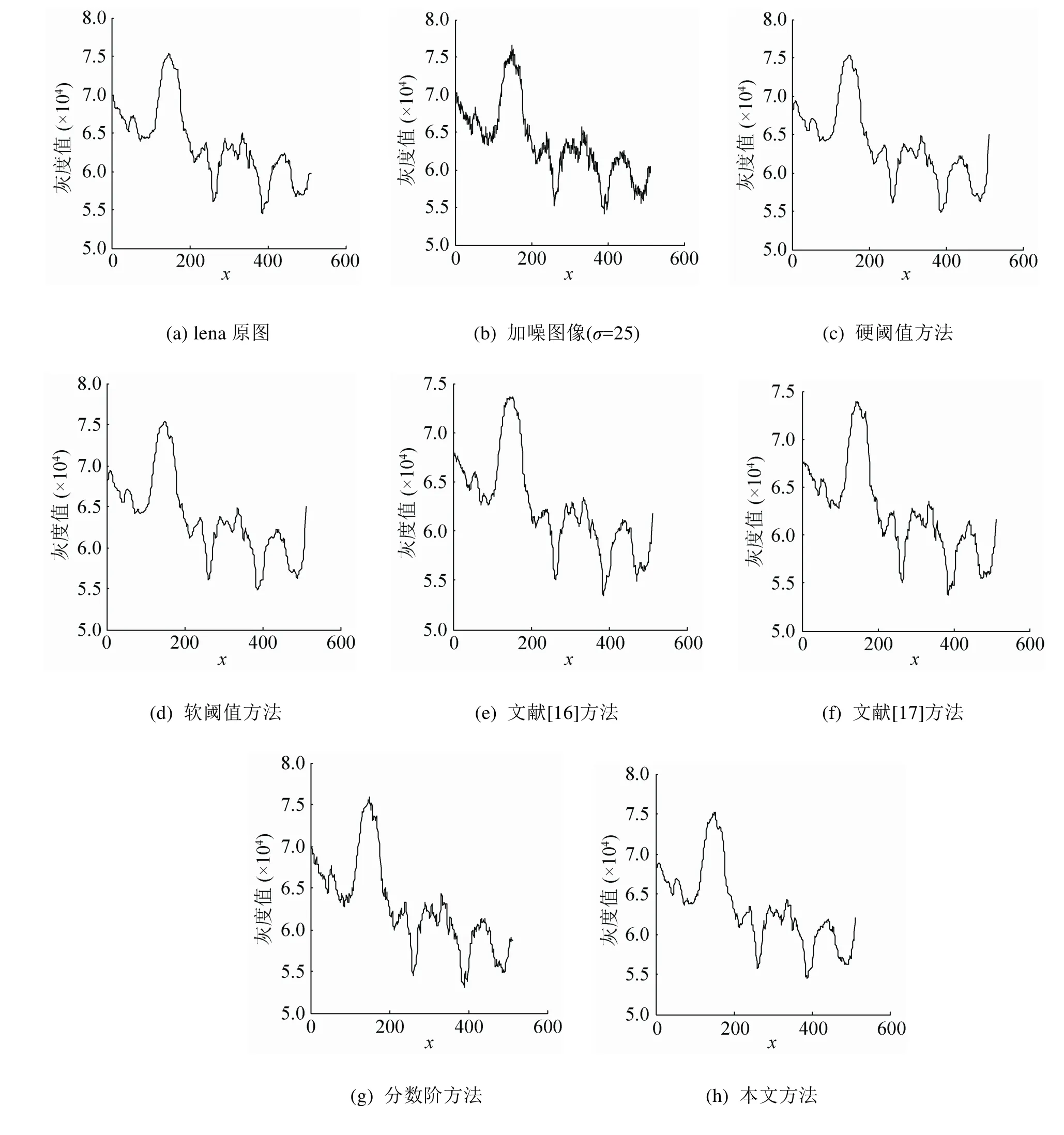
圖8 圖5中各圖的灰度值在x方向投影

由圖7～9可以看出，圖像在增加高斯白噪聲后圖像的灰度變化劇烈；Contourlet硬閾值方法去噪后圖像的灰度變化減弱，曲線變得平滑，在去噪的同時丟失了部分細節信息，使得圖像出現模糊現象；Contourlet軟閾值方法去噪后圖像的灰度曲線變化更加平滑，細節丟失嚴重，模糊現象加劇；文獻[16]方法去噪后的圖像灰度圖與原圖像基本一致，但整體灰度值偏低，而且曲線略微平滑表明局部細節信息有丟失現象；文獻[17]方法去噪后的圖像灰度變化與原圖基本保持一致，但在細節上的弱銳化現象將導致出現局部階梯效應；分數階方法去噪效果明顯，在去噪的同時對圖像的中低頻信息有所增強，圖像的紋理細節信息保留較好，但是曲線出現較多毛刺，表明部分區域出現銳化現象；文中所提方法具有軟、硬閾值的優點，同時避免了二者的缺點，去噪后圖像的灰度變化與原始圖像基本一致。該方法在去噪的同時能保留原始圖像紋理細節信息，特別是對圖像的邊緣細節有很好地保護，去噪效果明顯。

4.2 圖像去噪效果比較

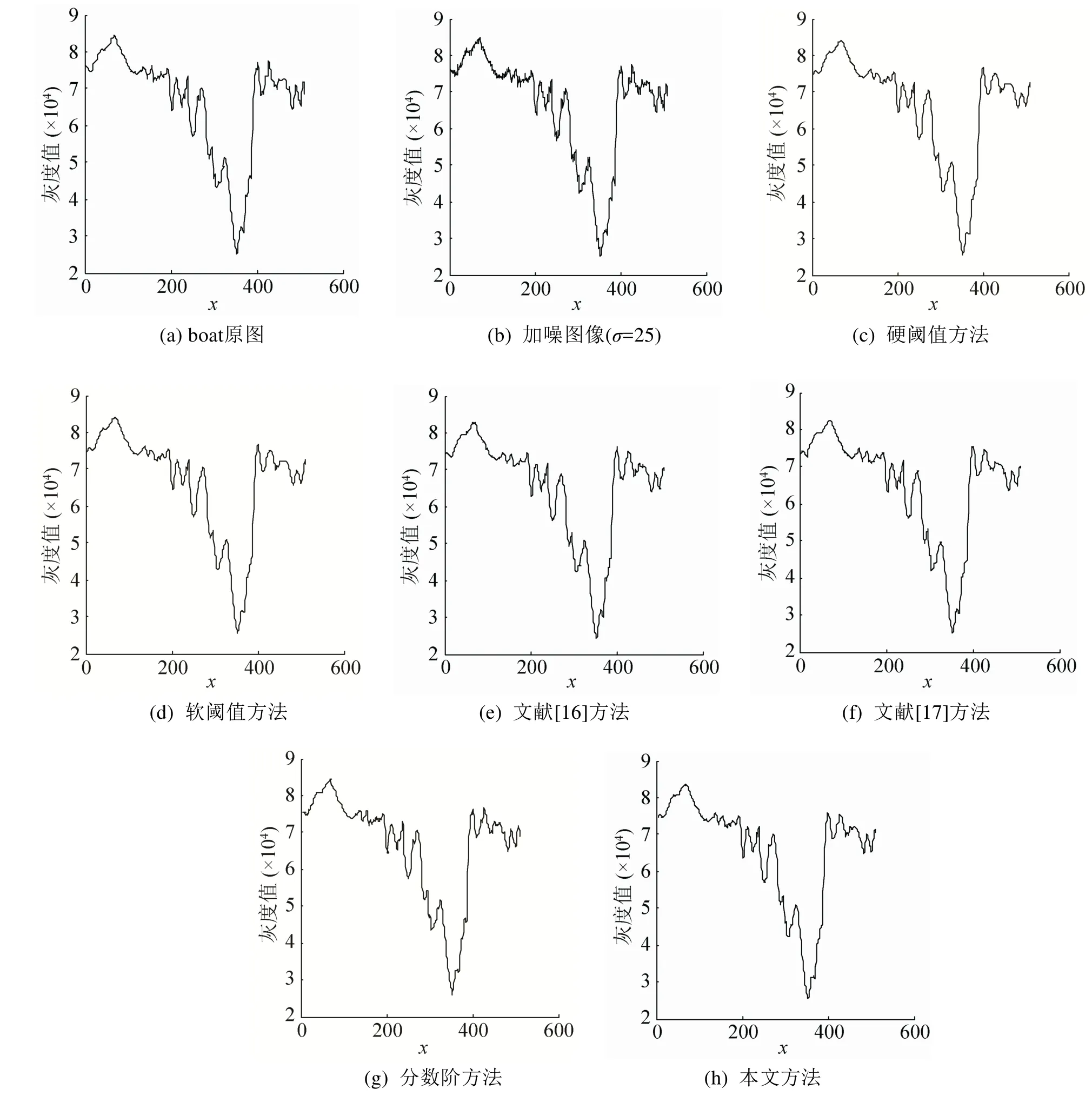
圖9 圖6中各圖的灰度值在x方向投影

設 Xin為原始圖像， Xout為增強后的結果圖像，(M ,N )為圖像的大小，Y為噪聲圖像，則：

(1) 均方根誤差：

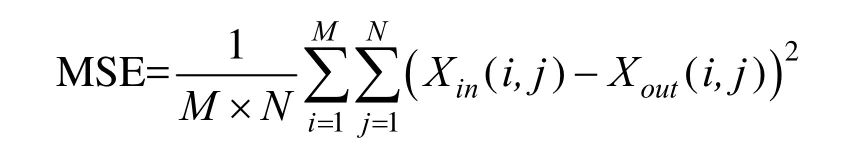
MSE是原圖像與處理圖像之間均方誤差，MSE值越小圖像去噪效果越好。

(2) 峰值信噪比：

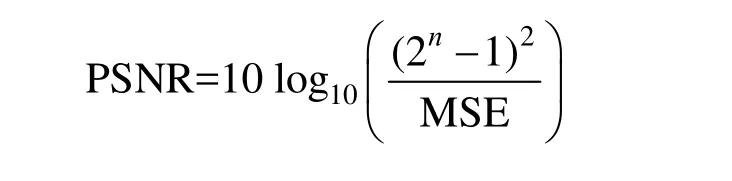
PSNR值越大圖像去噪效果越好。

(3) 圖像增強因子：

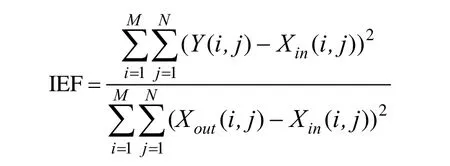
IEF用于評價算法的邊緣保留能力，值越大表示保留的圖像邊緣越多。

對peppers、lena和boat圖像分別應用硬閾值方法、軟閾值方法、文獻[16]方法、文獻[17]方法、分數階方法( v =-0 .8)及本文方法計算去噪后圖像的MSE、PSNR和IEF，計算結果如表1～3所示。

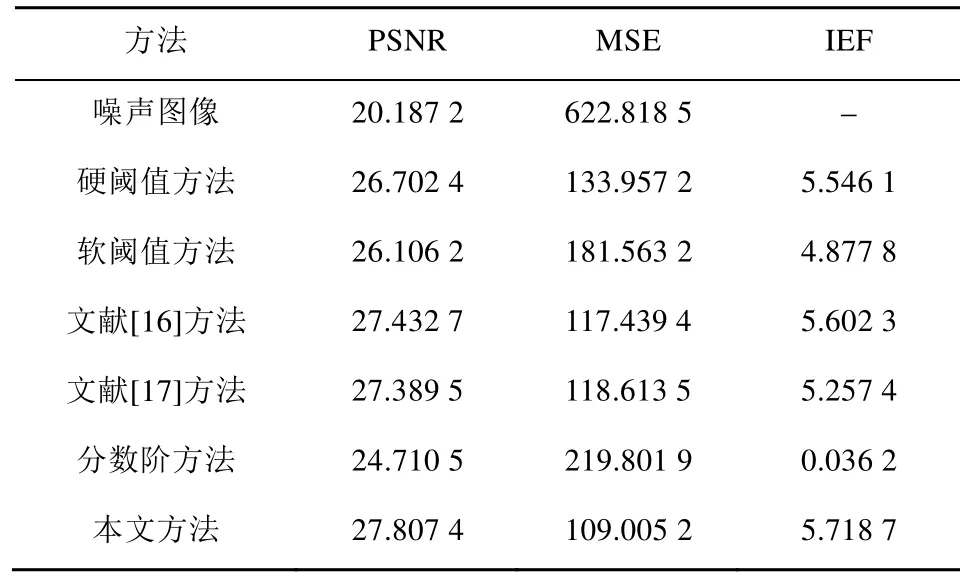
表1 圖4中peppers圖像各種去噪方法的指標比較

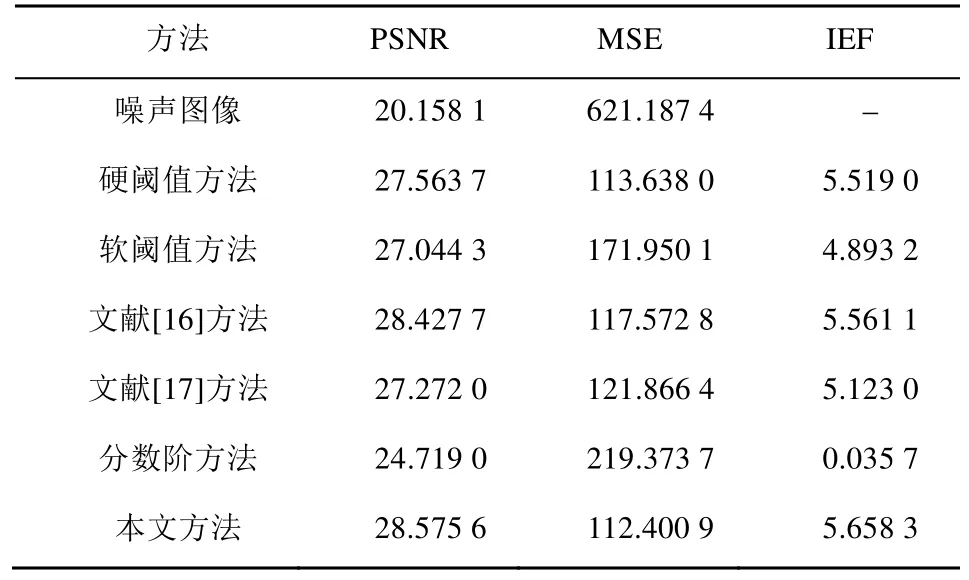
表2 圖5中lena圖像各種去噪方法的指標比較

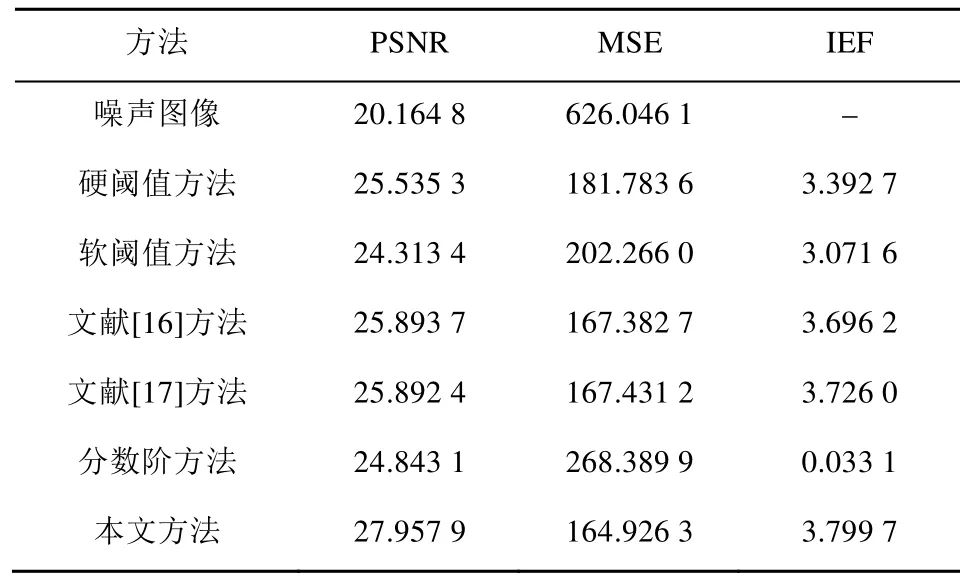
表3 圖6中boat圖像各種去噪方法的指標比較

由表1～3可知，采用分數階方法去噪圖像的MSE最高，PSNR和IEF最低，去噪質量較差；采用硬閾值方法和軟閾值方法去噪所得結果在MSE較高，PSNR和IEF的指標相對較低，造成圖像去噪的視覺效果比較差；采用文獻[16]方法和文獻[17]方法取得了較好的去噪，但各種指標略低；采用本文方法所得圖像PSNR最高，IEF也最高，而MSE最低，表明圖像的去噪效果最好。另外，由于本文方法的收縮函數系數是可變的，根據實際圖像的不同可采用收縮系數得到理想的去噪圖像。

4.3 運行時間比較

為了全面評估本文方法的性能，對peppers、lena和boat圖像分別增加不同高斯白噪聲σ的圖像進行去噪，并比較相關方法的核心算法運行時間，比較結果如圖10～12所示。其中，a表示文獻[16]方法；b表示文獻[17]方法；c表示分數階方法；d表示BM3D方法；e表示本文方法。

由圖10～12的各種去噪方法的運行時間比較可以看出，文獻[16]方法和文獻[17]方法的運行時間較少，隨著高斯白噪聲σ的增加運行時間增加不明顯；分數階方法的運行時間較長，隨著高斯白噪聲σ的增加運行時間逐步增加；BM3D方法運行時間介于分數階方法和改進閾值Contourlet變換方法之間，隨著高斯白噪聲σ的增加運行時間明顯增加；本文方法運行時間遠遠少于其他方法，而且高斯白噪聲σ的增加運行時間基本保持不變。

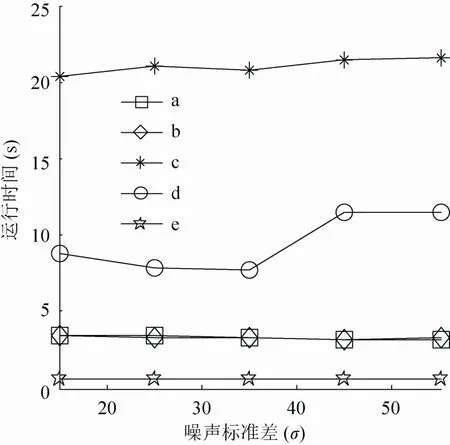
圖10 對peppers圖像去噪時各種方法運行時間比較

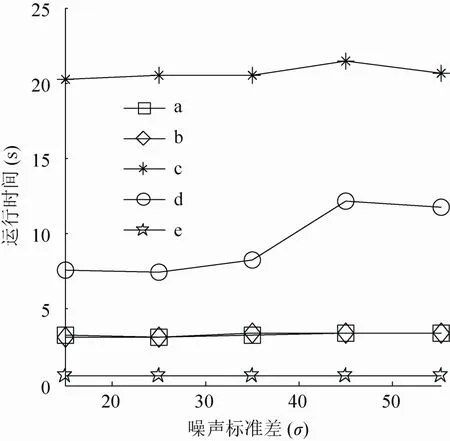
圖11 對lena圖像去噪時各種方法運行時間比較

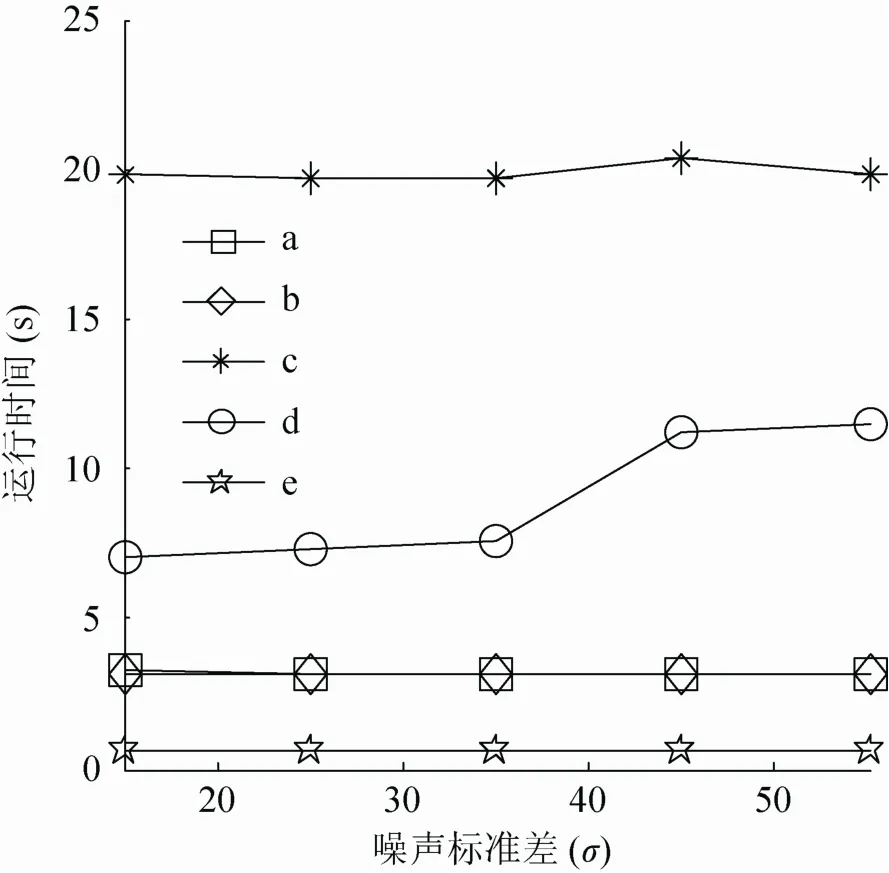
圖12 對boat圖像去噪時各種方法運行時間比較

5 結 束 語

將 Contourlet變換這種新的多尺度變換應用于數字圖像的底層處理是目前較新的研究課題。本文研究了Contourlet變換圖像去噪的原理，利用其在任意尺度上實現任意方向的分解、擅長描述圖像中的輪廓和方向性紋理信息的性質，提出了基于自適應收縮函數的Contourlet變換方法，該方法對收縮函數的系數 N1、N2及階數N的值可自適應選取，使得圖像的去噪效果得以提升。仿真實驗驗證了算法的有效性，表明該方法特別適用于對運行時間和去噪質量有較高需求的圖像去噪。但如何增強算法的自適應性是進一步要探討的問題。

[1] 楊農豐, 吳成茂, 屈漢章. 基于偏微分方程的混合噪聲去噪研究[J]. 計算機應用研究, 2013, 30(6): 1889-1902.

[2] 黃 果, 許 黎, 陳慶利, 等. 基于空間分數階偏微分方程的圖像去噪模型研究[J]. 四川大學學報, 2012, 44(2): 91-98.

[3] 盧兆林, 李閏龍, 李 濤, 等. 基于全變分理論的紅外圖像去噪[J]. 激光技術, 2012, 36(2): 194-197.

[4] Dabov K, Foi A, Katkovnik V, et al. Image denoising by sparse 3D transform-domain collaborative filtering [J]. IEEE Transactions on Image Processing, 2007, 16(8): 2080-2095.

[5] Danielyan A, Katkovnik V, Egiazarian K. BM3D frames and variational image deblurring [J]. IEEE Transactions on Image Processing, 2012, 21(4): 1715-1728.

[6] 李 偉, 楊 航. 曲波域經驗Wiener濾波[J]. 吉林大學學報: 理學版, 2013, 51(2): 312-316.

[7] 盧 艷, 潘英俊, 陶榮輝, 等. 基于輪廓波降噪的ISAR目標輪廓特征提取方法[J]. 儀器儀表學報, 2012, 33(10): 2293-2300.

[8] Dong Weisheng, Zhang Lei, Shi Guangming, et al. Nonlocally centralized sparse representation for image restoration [J]. IEEE Transactions on Image Processing, 2013, 22(4): 1620-1630.

[9] Xiang Shiming, Meng Gaofeng, Wang Ying, et al. Image deblurring with coupled dictionary learning [J]. International Journal of Computer Vision, 2014, 8: 1-24.

[10] 楊勝利, 高 雋, 孫 銳. 基于改良擴頻技術的Contourlet域盲圖像水印[J]. 工程圖學學報, 2011, 32(1): 52-58.

[11] Guo Qing, Dong Fangmin, Sun Shuifa, et al. Image denoising algorithm based on Contourlet transform for optical coherence tomography heart tube image [J]. IET Image Processing, 2013, 7(5): 442-450.

[12] Zhou Y, Wang J. Image denoising based on the symmetric normal inverse Gaussian model and non-subsampled Contourlet transform [J]. IET Image Processing, 2012, 6(8): 1136-1147.

[13] Sadreazami H, Ahmad M O, Swamy M N S. Contourlet domain image denoising using normal inverse gaussian distribution [C]//2014 IEEE 27th Canadian Conference on Electrical and Computer Engineering (CCECE). Toronto, Canada, 2014: 1-4.

[14] 任洪娥, 王海豐, 趙 鵬. 基于小波-Contourlet變換的Cycle spinning硬閾值圖像去噪方法[J]. 光學技術, 2008, 34(6): 854-857.

[15] 方 潔. 基于非抽樣 Contourlet變換的最佳軟閾值圖像去噪[J]. 計算機技術與發展, 2011, 21(2): 102-104.

[16] 唐 飛, 楊恢先, 曾友偉, 等. 改進的 Contourlet變換的圖像去噪算法[J]. 計算機工程與應用, 2014, 50(5): 132-136.

[17] 劉麗萍, 崔寧海, 王 琰. 一種新的Contourlet變換圖像降噪算法[J]. 沈陽理工大學學報, 2012, 31(1): 31-35.

[18] 胡金蓉, 蒲亦非, 周激流. 分數階積分的圖像去噪算法[J]. 電子科技大學學報, 2012, 41(5): 706-711.

[19] Burt P J, Adelson E H. The Laplacian pyramid as a compact image code [J]. IEEE Transactions on Communications, 1983, 31(4): 532-540.

[20] Do M N, Vetterli M. Framing pyramids [J]. IEEE Transactions on Signal Processing, 2003, 51(9): 2329-2342.

[21] Do M N. Directional multiresolution image representations [D]. Lausanne, Switzerland: Swiss Federal Institute of Technology, 2001.

[22] 肖進勝, 單珊珊, 段鵬飛, 等. 基于不同色彩空間融合的快速圖像增強算法[J]. 自動化學報, 2014, 40(4): 697-705.

Image Denoising Based on Adaptive Contraction Function Contourlet Transform

Niu Weihua, Meng Jianliang, Wang Ze, Cui Kebin
(School of Control & Computer Engineering, North China Electric Power University, Baoding Hebei 071003, China)

To solve some problems on image denoising, such as losing details and falling into poor effects, a method of image denoising is proposed based on adaptive contraction function Contourlet transform algorithm. According to the basic Contourlet transform form and combing the soft threshold and hard threshold contraction function, the adaptive contraction function is defined. Experimental results show that the proposed method can greatly remove noise, effectively improve peak signal to noise ratio, mean squared error and image enhancement factor of image quality index. After combining the improved threshold function, the image has better visual quality.

Contourlet transform; adaptive contraction function; contract order; soft threshold; hard threshold

TP 391

A

2095-302X(2015)04-0593-10

2014-09-25；定稿日期：2015-03-09

中央高校基本科研業務費資助項目(2014MS133)

牛為華(1978–)，女，天津人，講師，博士。主要研究方向為圖像視頻處理、圖像處理技術在電力系統中的應用。E-mail：tusiniuweihua@163.com