三維地質模型的一種快速建模方法研究

陳續威，謝凱，劉波，張圳，白志君 長江大學電子信息學院

長江大學油氣信息處理與識別研究所，湖北 荊州434023

隨著復雜幾何模型建模的需求日益增加，快速建模技術也應運而生。在計算機圖形學領域，經常采用多邊形網格來描述物體的幾何模型。對于小數據量的地質模型，采用一般的建模技術足以滿足要求，但是對于復雜不規則的地質模型（如包含斷層、褶曲、開挖邊界等），其網格通常由成千上萬個多邊形面片組成［1，2］。由于將多邊形映射為圖像的過程需要進行大量計算，因而花費的繪制時間相當長，存儲量也特別大。隨著地質學研究的深入，數據量龐大的復雜地質模型通常不能滿足實時繪制的需要。為此，筆者對三維地質模型的一種快速建模方法進行了研究，以便能夠在保持較高逼真度的前提下實現運算速度的大幅提升以及模型的大幅度簡化，從而滿足實時繪制的需要。

1 建模原理與流程

三維地質模型的快速建模方法的基本原理是通過刪除一部分在精度范圍內的頂點，即減少運算數據的方式，從而達到加快建模速度的目的［3，4］。三維地質模型的快速建模方法流程圖如圖1所示。

2 建模過程

2.1 計算法矢量

讀取文件中的地質網格數據，將地質數據進行三角形細分后，任取一個交點，計算出周圍所有三角形的法矢量，求出平均值，作為該點的法矢量，并進行歸一化處理。依此類推，可以計算出所有網格點的單位法矢量。

對于復雜地質體的網格模型，為了提高其建模的精確度，采用6個點（其中有2個重點）畫2個三角形的方式進行三角形細分（見圖2），可得到三角形面的個數為2＊（columns＊rows），對得到的三角形面片，根據其3個頂點可以唯一確定該三角面片的法矢量，具體方法如下［5］。

圖1 三維地質模型的快速建模方法流程圖

設三角形的3個點分別為A、B、C（逆時針排列），其法矢量為→h，則：

三角形細分后，對網格面中的任意一個交點q，其周圍將存在n個（此處n＝6）三角形（見圖2）。

設第i個三角形的單位法矢量為（i＝1，2，…，n），則交點q的法矢量可用其周圍所有（此處為6個）三角形面的法矢量的平均值來表示，若表示交點q的法矢量，則：

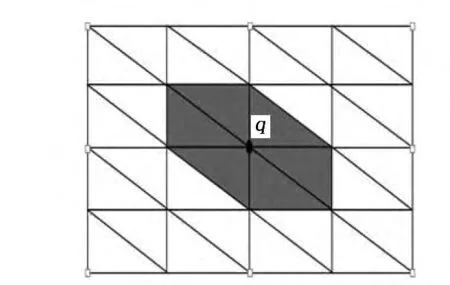
圖2 模型網格面及其三角形細分

由于的模值分布區間較大，不易后續處理，現對其進行歸一化（即取模為1），設歸一化后的單位法矢量為，則：

式（3）即為平均后的單位法矢量，現將其定義為復雜地質網格面交點q的單位法矢量。

2.2 修正法矢量

某一點修正后的法矢量是由周圍所有網格交點的單位法矢量所共同決定的，算出其平均值，即為該點修正后的法矢量。為了提高復雜地質模型處理后的逼真度，根據某一網格點周圍所有點的單位法矢量，求出其平均值作為該點修正后的法矢量。點q修正后的單位法矢量是周圍所有點單位法矢量的平均值（見圖3），由此可以算出周圍8個點，，…，的單位法矢量。修正后的法矢量用表示，即：

圖3 網格交點及其法矢量平均

2.3 數據簡化

模型簡化算法是在給定精度ε的條件下，求出某一網格點與周圍點修正后的法矢量的夾角θ，將求得的夾角θ換算成弧度值后與設定的精度值ε進行比較，由此決定是否刪除該網格點。

在一定的精度范圍ε內，利用模型簡化算法對所有點進行有選擇性的刪除。從視覺效果看，當多個點的法向量的方向近似相同時，它們所構成的曲面近似平緩，此時在一定精度范圍內，部分數據是不必要的（見圖4）。在這種情況下，可以刪除不必要的數據，從而實現地質模型的快速建模。設置繪制精度為ε，周圍點的修正法矢量為（i＝1，2，…，8），計算出某一網格點 （非邊界點）與周圍點的修正法向量所組成的夾角θi：

圖4 曲面的一維數學模型圖

設：

當δi（i＝1，2，…，8）小于繪制精度ε時，表明周圍的點與該網格點的修正法矢量相差不大，即周圍8個點對該點的影響是可以接受的，此時可以刪除該網格點。由于反余弦函數在 ［－1，1］區間內呈單調遞減，故可將表達式：

轉化為：

令N＝cos（επ），則：

當δi（i＝1，2，…，8）不全小于繪制精度ε時，則表明周圍的點中存在與該網格點的修正法矢量相差較大的點，此時將保留該網格點。此外，邊界點將全部保留。

2.4 數據重構

對處理后的數據進行三角形網格重構，采用改進后的分治算法，生成三角網。在重構過程中，首先利用八叉樹算法［6］對已篩選過的地質數據進行分塊處理和存儲，若某塊內的數據是不勻質的，則再次進行八叉樹劃分，塊內的地質數據勻質時則不必再次分塊。然后，將分塊后的數據放到GPU線程塊中，再將非勻質塊細分給每個塊內線程，利用GPU同一線程塊的線程可以相互通信的優勢，讓指向各個不同地質信息數據的指針能夠在線程間并行移動，由此防止指針出現混亂。此外，每個線程塊還要進行同步處理，保證每個線程都能完成其相應的計算。

3 試驗結果與分析

采用某地區的地質體數據進行試驗以檢驗上述方法。該模型為985×748的網格數據，原始網格點數目為736780。對模型數據進行了3次簡化，然后計算了簡化比、平均交互速度和對稱Hausdorff距離（見表1）。分析表1數據可知，隨著頂點數的減少，三角形面片數也減少，簡化比增加，平均交互速度增加，這說明建模速度加快。采用對稱Hausdorff距離來評估的模型的幾何相似度，對稱Hausdorff距離實際上是2個網格模型之間的最大誤差，對稱Hausdorff距離越小，2個網格模型之間的幾何相似度越大。從表1數據還可以看出，隨著刪除的頂點數的增加，對稱Hausdorff距離增大，幾何相似度下降。

表1 某地區地質模型試驗數據

為了直觀地表示試驗結果中刪除的網格點和保留的網格點，將該網格點轉化為985×748的平面圖像。對于每個模型，采用3種顯示方式，分別為點顯示（見圖5）、網格顯示（見圖6）和三角面片顯示（見圖7）。可以看出，圖5和圖6清晰地顯示了保留的網格點。此外，從圖7的4幅圖片可以看出，雖然頂點數減少，但模型的相似度仍然較高。

4 結語

提出一種通過對數據的簡化來實現三維地質模型快速建模的算法，在一定的精度范圍內，根據三角形面片的法矢量對一些數據進行刪除，在數據處理的過程中，利用GPU強大的計算能力，對處理后的數據進行重構，達到快速建模的目的。試驗結果表明，利用該方法能夠在保證較高相似度的前提下實現模型的簡化和建模速度的提高，因而該方法是可行的。

圖5 各模型點顯示圖

圖6 各模型網格顯示圖

圖7 各模型三角面片顯示圖

［1］Wang Gongwen，Zhu Yanyan，Zhang Shouting，et al.3Dgeological modeling based on gravitational and magnetic data inversion in the Luanchuan ore region ［J］.Journal of Applied Geophysics，2012，80（1）：1～11.

［2］Tame C，Cundy A B，Royse K R，et al.Three－dimensional geological modelling of anthropogenic deposits at small urban sites：A case study from Sheepcote Valley ［J］.Journal of Environmental Management，2013，129（15）：628～634.

［3］李舒，李偉波，宋世鵬 .三維地質建模的應用研究 ［J］.科學技術與工程，2008，24（8）：9584～9587.

［4］劉少華，吳東勝，羅小龍，等 .復雜地質體的三維建模與可視化方法的研究 ［J］.礦業研究與開發，2007，27（2）：56～58.

［5］Wycisk P，Hubert T，Gossel W，et al.High－resolution 3Dspatial modelling of complex geological structures for an environmental risk assessment of abundant mining and industrial megasites ［J］.Computers ＆ Geosciences，2009，35（1）：165～182.

［6］Jing Ming，Mao Pan，Honggang Qu，et al.GSIS：A 3Dgeological multi－body modeling system from netty cross－sections with topology ［J］.Computers ＆ Geosciences，2010，36（6）：756～767.