土-結構體系的混合約束模態法在ANSYS中實施研究1

姜忻良 溫 新

?

土-結構體系的混合約束模態法在ANSYS中實施研究1

姜忻良 溫 新

（天津大學建筑工程學院/濱海土木工程結構與安全教育部重點實驗室（天津大學），天津 300072）

為了使提出的線性-非線性混合約束模態綜合法能在商業軟件中得到應用，本文對該方法在ANSYS軟件中的運用進行了研究。對ANSYS中的超單元進行了深入分析，將線性-非線性混合約束模態綜合法線性部分的處理作為超單元生成的過程，并根據基于勢能判據的截斷模態準則，運用Matlab自編了程序，求得子結構的截取主模態數，對存在局部非線性的土-高層框架結構相互作用進行了地震反應分析；進而對采用粘彈性人工邊界與自由邊界狀況進行了比較，討論分析了兩種土體邊界對線性-非線性混合的約束模態綜合法自由度縮減的影響。

土-結構相互作用 混合約束模態法 線性-非線性 超單元

引言

我國處于地震多發區，自2008年汶川地震以來，結構的抗震問題越來越受到工程界的高度關注。在抗震研究的初期，人們已經認識到建筑物的震害與地基條件密切相關（呂西林，2007），因此在高層建筑的抗震分析和設計過程中十分有必要考慮土-結構的相互作用問題（林皋，1993）。在現有計算方法中，動態子結構法具有降低體系自由度、提高計算效率、節省計算時間的優點，已被廣泛應用到土-結構相互作用的分析實踐中。由于動態子結構法是在振型疊加的基礎上建立的（白建方等，2008），故其在非線性結構的應用中受到了一定的限制。然而在土-結構動力響應的分析中，人們往往會截取大范圍的土體來模擬土體的半空間無限性，研究表明，地震作用下僅僅在結構基礎周圍的土體發生塑性變形，進入非線性階段，而離結構較遠的土體一直處于線性階段，對于此類存在局部非線性體系的研究，采用常規有限元方法進行整體非線性分析時存在計算時間較長，計算成本較高的問題。

針對此問題，姜忻良等（2010）提出了線性-非線性混合的約束模態綜合法理論。該方法在考慮土體的非線性特性的同時，能夠極大程度的縮減整體體系的自由度，降低計算成本，為土-結構相互作用的研究提供了新的思路。為了使這一理論與方法得到廣泛應用，本文以土-高層框架相互作用體系為研究對象，將線性-非線性混合的約束模態綜合法理論運用到ANSYS大型通用軟件的實踐中，并在此基礎上研究了粘彈性土體邊界對線性-非線性混合的約束模態綜合法的影響。

1 線性-非線性混合的約束模態綜合法

在許多實際工程中，整體結構在荷載作用下，并非全部構件都進入非線性階段，而是僅僅在某些位置才出現非線性特征，這說明結構存在局部塑性區域的特點。而土與結構相互作用問題就是一個典型的例子，在地震響應分析中，僅僅與上部結構鄰近的地基土區域會產生塑性應變，出現非線性特征，而遠離上部結構的地基土區域在整個加載過程中卻始終處于線性階段。線性-非線性混合的約束模態綜合法就是根據結構體系的這一特點，將體系劃分為若干線性子結構和非線性子結構，然后運用約束模態綜合法對線性子結構進行自由度縮減，而對非線性子結構不作縮減，通過邊界節點的位移協調條件和力協調條件與線性子結構組成整體非線性運動方程進行求解。下面以土-結構相互作用體系為例進行分析。

對于圖1（a）所示的土-結構體系，將在整個加載過程中一直保持線性特性部分的土體分別劃分為線性子結構α、β、γ、δ，將結構周圍進入非線性狀態的部分土體、地下室和框架結構獨立劃分為非線性子結構ω。

對于線性子結構，以子結構為例，來說明子結構自由度的縮減過程。根據約束模態綜合法（Craig等，1968），線性子結構內任一點的位移可由約束模態位移和固定對接主模態位移兩部分組成。同時將線性子結構的節點進行分塊，如圖2所示，未編號節點為內部節點，編號1—16的節點為邊界節點，則子結構的位移向量根據內部節點（用下標表示）和邊界節點（用下標表示）可分塊表示為：

其中，q為Ritz基，是結構的廣義坐標系，為結構的坐標變換矩陣，其表達式為：

（2）

其中，是子結構截取前階主模態獲得的，是子結構的約束模態矩陣。

根據運動學可知，子結構的運動方程為：

其中，、分別為子結構的質量、阻尼、剛度、荷載矩陣。

將式（3）按照內部節點和邊界節點進行分塊處理可寫為：

將式（1）代入式（4），且方程兩側均左乘T（的轉置），可得到線性子結構在廣義坐標下的運動方程為：

（5）

同理，可得到線性子結構在廣義坐標下的運動方程，表達式與式（5）相同，只需改變上角標。

對于非線性子結構，不做自由度的縮減，將其運動方程按照內部節點和邊界節點的形式分塊表示為：

如圖1（a）所示，非線性子結構的邊界同時與線性子結構耦合，其位移與力的協調條件極為復雜，應采用如下協調條件：

（7）

其中，上角標表示該向量所屬的子結構名稱，帶括號的下標表示與該子結構邊界耦合的子結構名稱。結合式（5）—（7），根據力協調與位移協調條件，形成整體體系的運動方程：

（8）

采用合適的非線性方程求解方法對式（8）進行求解，可得到線性子結構在廣義坐標下的位移解和非線性子結構在物理坐標下的位移解，最后通過一次坐標變換，即可得到線性子結構在物理坐標下的位移解。

2 高層框架結構與地基相互作用的地震分析

由上述理論可知，線性-非線性混合的約束模態綜合法是約束模態綜合法的推廣，故其應用也是以約束模態綜合法的應用為基礎的。下面以圖1所示的土-結構體系為例，給出線性-非線性混合的約束模態綜合法在ANSYS軟件中的應用。

在圖1（a）中，土體區域的邊界沿結構基礎邊界兩側各取120m（5倍的基礎寬度），則總寬度為264m，深度取72m。研究表明，塑性土體區域一般僅在基礎附近區域，為保險起見，其高度取20.6m，寬度取120m，各土層厚度1—5以及地質參數見表1。地基最下層土體為理論基巖，視為固定端。本文選用了足夠大范圍的土體，故土體側向邊界采用自由邊界。由圖1（b）可知，框架結構每跨跨度為4.8m，層高為3m，箱型基礎的空間做成地下室，地下室層高為3.3m，樓板厚度為0.5m。柱子的截面尺寸為800mm×800mm，梁的截面尺寸為250mm×600mm，框架結構和地下室均為鋼筋混凝土材料。將體系按照圖1（a）所示劃分為5部分，除了結構為非線性子結構外，結構均為線性子結構。

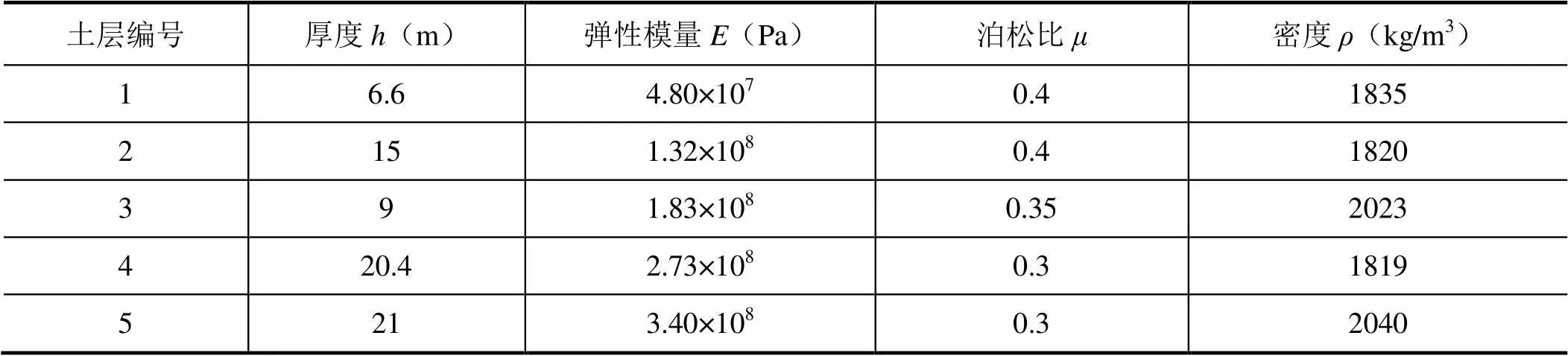
表1 地基地質參數

2.1 線性子結構模型的建立

子結構法在ANSYS軟件中的應用是將線性子結構凝聚為一個單元的過程（王新敏，2007），此單元在ANSYS中稱為超單元。故線性-非線性混合約束模態綜合法對線性部分的處理也是超單元生成的過程。下面以線性子結構為例說明超單元的生成過程。

按照常規方法建立子結構的有限元模型，將超單元與其它單元連接的邊界節點定義為主自由度。為了使縮減后的子結構能保證其精度，確定截取子結構的主模態數的取值，本文根據基于勢能判據的截斷模態準則（姜忻良等，2011）的原理，運用Matlab計算軟件自編了程序，求得如圖3所示的勢能隨著截取主模態數的變化曲線，根據變化曲線進而確定為79。最后求解生成超單元，提取動力特性矩陣。用同樣的方法，還可得到子結構的動力特性矩陣。

2.2 建立整體體系

按照常規方法建立非線性子結構ω的有限元模型，并導入各個線性子結構生成的超單元，耦合主自由度，連接各個超單元以及超單元與非超單元，形成整體體系。

2.3 施加荷載并求解

根據地質情況和《建筑抗震設計規范（GB50011-2010）》（中華人民共和國建設部，2010）選取適合該類場地土的天津波、EI-Centro波（南北向）以及Traft波，調整其地震波加速度峰值為3.10m/s2。如圖4所示。在地面（即箱型基礎頂部）輸入地震波進行地震時程響應分析，并用Newmark-法進行求解，最終得到線性子結構在廣義坐標下的解和非線性子結構在物理坐標下的解。

將所得到的各個線性子結構在廣義坐標下的位移解通過超單元的擴展過程即可得到其在物理坐標下的位移解，從而得到整個體系的位移解。

2.4 結果分析

為了驗證本文方法所得結果的可靠度，同時采用了整體有限元法（網格劃分相同）進行了計算，以下給出兩種計算方法所得部分結果（見圖5）。

表2、表3中max、max、max分別為結構頂點A點的位移、速度、加速度的最大值，max、max分別為柱子B處剪力、彎矩的最大值。

表2 頂點A的Umax、Vmax、Amax

表3 柱子B的Fmax、Mmax

由圖5可知在天津波作用下兩種計算方法所得框架A點的位移、速度、加速度時程曲線吻合良好。由表2、表3的數據可知，兩種不同計算方法所得結果中，A點地震響應和B柱內力最大值的相差均在5%以內，表明在ANSYS分析軟件中運用線性-非線性混合的約束模態綜合法和整體有限元法進行結構的地震分析吻合良好。采用本文方法建模的自由度數為2173，與采用整體有限元方法建模的自由度數5294相比減少了59%，由此可見線性-非線性混合的約束模態綜合法，在進行土-結構相互作用分析中能大幅度縮減體系自由度，節約計算時間，降低計算成本，并且可以在ANSYS分析軟件中實現。

3 粘彈性土體邊界對混合約束模態綜合法的影響

在以上分析中，由于土體區域取得相當大，故土體邊界選為自由邊界，為考察土體邊界條件取法對線性-非線性混合的約束模態綜合法的適用性以及對自由度縮減的影響，本文將土體邊界考慮為粘彈性人工邊界，即在土體邊界施加一組彈簧-阻尼器。由于粘彈性邊界能很好地模擬土體在地震反應中對地震波能量的吸收和土體的恢復性能，能夠通過較小范圍的土體模擬半空間無限土體（劉晶波等，2007），故本例題中結構邊界到土體邊界的長度為96m（4倍的基礎寬度）。

采用粘彈性人工邊界后，涉及到邊界的子結構的運動方程會有所改變，現以線性子結構為例進行推導。

在子結構左邊設置粘彈性邊界后，子結構的節點由圖2的兩部分變為圖6所示的三部分：編號1—4為粘彈性邊界節點；編號5—19為連接節點；未編號的節點為內部節點。則子結構的位移按內部節點（用下標表示）、連接節點（用下標表示）和粘彈性人工邊界節點（用下標表示）分塊表示為：

（9）

其中轉換矩陣也由三部分組成：

子結構α的運動方程式（3）也分塊表示為：

（11）

將式(12)代入式(11)，整理得：

（13）

將式(10)代入式(13)，并且在等式左右兩端均左乘T，得到子結構經過坐標變換的動力方程為：

同理，可得到其他與粘彈性人工邊界相連的子結構在廣義坐標下的動力方程，根據各個子結構之間邊界節點的位移協調和力協調條件裝配成整體體系的動力方程，然后進行求解。

現僅給出天津波作用下的結果，并與采用自由邊界體系的計算結果進行對比。

表4 兩種邊界條件的計算結果的比較

表5 兩種邊界條件下子結構截取的主模態數

由圖7和表4可以看出，兩種邊界條件下的計算結果幾乎相等，表明運用線性-非線性混合的約束模態綜合對體系進行地震分析時，采用自由邊界和粘彈性人工邊界計算時具有相同的精度。由表5可以看出，兩種邊界條件下線性子結構所截取的主模態數相差不大，且采用粘彈性人工邊界體系的總自由度數比采用自由邊界體系的僅少了0.6%，這是因為子結構的邊界節點不能縮減，采用粘彈性人工邊界的體系中邊界節點數目較多，在一定程度上增加了整體體系的自由度數。眾所周知，有限元整體法中人工邊界的設置是減小有限元模型規模的有效方法，而在線性-非線性混合約束模態綜合法中，其效果卻不明顯，應綜合考慮子結構邊界節點的增加與截取的主模態數兩者的關系。

4 結論

本文對線性-非線性混合約束模態綜合法在ANSYS軟件中的應用進行了研究，對存在局部非線性的土-高層框架結構相互作用進行了地震反應分析，得到如下結論：

（1）線性-非線性混合約束模態綜合法能解決體系中局部非線性問題，尤其適合解決土-結構相互作用土體中出現的局部非線性問題。

（2）將線性-非線性混合約束模態綜合法線性部分的處理作為ANSYS中超單元生成的過程，并根據基于勢能判據的截斷模態準則，應用Matlab計算軟件自編了程序，求得子結構的截取主模態數，得到的結果滿足精度要求。

（3）采用線性-非線性混合約束模態綜合法與整體有限元方法相比能有效縮減體系的自由度，而采用不同人工邊界對混合約束模態綜合法效果則不明顯，應綜合考慮子結構邊界節點的增加與截取的主模態數兩者的關系。

白建方，樓夢麟，2008．基于動力子結構方法的場地地震反應分析方法．震災防御技術，3（2）：145—154．

姜忻良，王菲，2010．線性-非線性混合的約束模態綜合法及實踐. 天津大學學報，43（5）：385—391．

姜忻良，王菲，2011．基于勢能判據的約束模態綜合法截斷準則. 振動與沖擊，30（2）：32—38．

呂西林，2007．復雜高層建筑結構抗震理論與應用．北京：科學出版社.

林皋，1993．土-結構相互作用對高層建筑非線性地震反應的影響．土木程學報，26（4）：1—13．

劉晶波，杜義欣，閆秋實，2007．粘彈性人工邊界及地震動輸入在通用有限元軟件中的實現．防災減災工程學報，27（增刊）：37—42．

王新敏，2007．ANSYS工程結構數值分析．北京：人民交通出版社．

中華人民共和國建設部，2010．建筑抗震設計規范（GB 50011-2010）．北京：中國計劃出版社．

Craig R.R.Jr，Bampton M．C．C，1968．Coupling of Structures for Dynamic Analyses．AAIA Journal，6（7）：1313—1319.

Application Research of the Mixed Constrained Mode Synthesis Method of Soil - Structure System in ANSYS

Jiang Xinliang and Wen Xin

(School of Civil Engineering, Tianjin University／Key Laboratory of Coastal Civil Engineering Structure and Safety (Tianjin University), Ministry of Education, Tianjin 300072, China)

In order to research the applicability of the mixed linear-nonlinear constrained mode synthesis method in commercial software, this contribution presents this method in ANYSYS software. The super element in ANSYS is analyzed, and the linear part of the mixed linear-nonlinear constrained mode synthesis method is processed as generation process of super element. In order to capture the cut main modal number in the substructure, the program of Matlab is compiled according to the mode cut-off criterion based on potential energy criterion. And seismic analysis of soil-high-rise frame structure interaction that exist local nonlinear is carried. The comparison of structure with the viscoelastic artificial boundary and structure with free boundary condition is conducted. The discussion on the influence of the two kinds of soil boundary to the reduced freedom degrees of the mixed linear-nonlinear constrained mode synthesis method is proposed.

Soil-structure interaction; The mixed constrained mode method; Linear-nonlinear; Super element

國家自然科學基金項目(51178308)，國家自然科學基金項目(51278335)

2015-02-03

姜忻良，男，生于1951年。博士，教授。從事結構－地基相互作用地震反應分析。E-mail：jiangxinliang@126.com