一種帶剪切約束的啟發式二維裝箱算法

姚　怡， 賴朝安

(1. 華南理工大學工商管理學院，廣東 廣州 510640；2. 廣西大學計算機與電子信息學院，廣西 南寧 530004)

一種帶剪切約束的啟發式二維裝箱算法

姚怡1,2， 賴朝安1

(1. 華南理工大學工商管理學院，廣東 廣州 510640；2. 廣西大學計算機與電子信息學院，廣西 南寧 530004)

提出一種滿足剪切約束的啟發式二維裝箱算法，通過價值修正策略提高箱的空間利用率，進而減少箱的使用數量。該啟發式算法將較難裝箱的物品賦予較高的價值及裝箱優先權；并通過延展或融合剩余零散空間，將未用的空間合并到剩余相鄰空間，以改進空間利用率。基于標桿測試數據集的仿真實驗證明了該算法的有效性和相較于其他二維裝箱算法的優越性。

二維裝箱；價值修正；剪切方式；啟發式

二維裝箱(two-dimensional bin packing，2DBP)問題作為一個典型的組合優化問題吸引了大量集中于數學模型或算法的研究，近期的研究則更加關注大規模的裝箱問題，對此通常不是采用系統的、精確的方法追求問題的最優解，而是采用確定性算法對解的生成方式加以一定的限制，在可接受的時間內獲取較優解[1-2]；或者采用各種啟發式算法[3-10]，通過不斷嘗試逐步趨優的方法，達到有效合理的目標，取得足夠滿意的解。2DBP的研究主要關注輸出(價值)最大化與輸入(價值)最小化兩項指標，以達到裝箱效率的最大化。本文研究以輸入最小化為目標的2DBP多箱問題，該問題可描述為：給定固定尺寸的多個二維矩形箱，其寬度為W，高度為H；存在大量在尺寸上差異較大的二維矩形物品，現需尋找能裝入所有物品的、且保證物品不重疊并呈現正交擺放形式的裝箱方案，達到所使用的箱數量最小化的目標。

定向與剪切這兩種約束的組合產生4種2D裝箱方式：OF、RF、OG和RG[3]。O是指矩形物品只能定向裝箱(orientated，O)，R則相反，允許物品旋轉(rotatable，R)；G是指物品必須采用類似剪床的“一刀切”工藝的擺放布局，即剪切方式(guillotine-cut，G)；而F則相反，允許物品自由擺放。本文研究2種情況：2DBP-OG和2DBP-RG。

2002年Lodi等[7]針對4種2DBP類型(OF、RF、OG和RG)提出了一種啟發式算法，同時設計了一個統一的禁忌搜索算法，在鄰域的探索中通過改變啟發性規則去適應裝箱類型的變化。1999年Lodi等[3]提出了背包裝填算法(knapsack problem，KP)，采用了基于所產生子問題的另一個層裝填策略。在(兩值)背包問題中，必須選擇n個元素的一個子集，每個元素有相應的利潤和重量，使總重量不超過給定的容重并且總利潤達到最大。2009年Polyakovsky和M′Hallah[8]提出了基于代理的智能算法(agent-based，A-B)，以剪切型左下原則(guillotine bottom-left，GBL)做物品的基礎裝填，并設置了物品的代理機制，每個代理擁有自己的參數、適應度和判定過程，通過代理間的相互影響，決定物品的最佳裝填位置。2011年Charalambous和Fleszar[9]針對帶剪切約束的2DBP提出了一個啟發式算法，采用平均面積的策略選擇物品并逐個箱子裝填，有效避免了因單純追求箱子的面積利用率而導致小物品的過度使用。2013年Fleszar[10]針對2BP-OG/RG問題構造了3個插入型啟發式算法，通過樹型結構去描述物品布局以及物品的各種插入操作，并設計了新的判定規則用于改善算法效果。

1　本文算法

針對裝箱過程中，由于某些物品過度使用而產生局部最優而非全局最優的現象，Belov提出順序價值修正策略(sequential value correction，SVC)。通過不斷修正物品價值來達到全局優化的目的，并將該方法成功運用于一維下料問題[11]和帶排樣問題[12]，取得較好的效果。本文的二維裝箱算法借鑒了Belov提出的價值修正策略，具體如下：

(1) 對每個物品設定初始價值，形成價值不等的候選物品集合A；

(2) 從集合A中選擇要填充的若干物品形成集合B，并沿高度方向ih對物品非增序排列，采取左下角原則做基礎填充，形成階梯狀的物品填充布局P；

(3) 選擇位于階梯上方的某個矩形空間s，對其進行裝箱；

(5) 每當一個箱子裝滿了或剩余空間已經無任何利用價值時，就打開另一個新的空箱繼續裝填直至剩余物品為0，此時獲取一個裝箱方案C；

(6) 采用價值修正公式對每個物品價值進行修正，形成附帶新價值的物品集合，重新裝箱，獲得新的裝箱方案，經過若干次的迭代，選取最優裝箱方案作為結果。

主算法偽代碼如下：

算法1. Main()

1.1物品初始價值設定

價值修正策略是為了在迭代過程中能更快更好地逼近最佳結果，在每一次迭代開始時，將前一次迭代的結果傳遞過來，作為參數調節本次迭代的初始值。本文方法在每輪裝箱方案生成后均對所有物品重設價值，采用價值修正的方式調整裝箱布局，使得難裝的物品(價值大)先行填充。衡量每個箱子的裝箱布局的好或壞，不再是單純的面積利用率，而是改成所裝物品總價值最大化。在首輪裝箱方案中，需要給每個物品一個初始價值。根據經驗，一般面積越大的物品填充難度越大，因此直接設置物品面積為初始價值。設箱子尺寸為HW×，需對矩形物品集合A=進行裝箱。裝箱之前，根據式(1)賦予每個物品 ai一個初始價值 vi：

1.2空間填充方法(pack(r,B))本文算法除了定義物品集合A，還定義了空間集合用來存放當前箱子中可供填充的各種矩形空間信息。為方便描述，將已有或即將有物品填充的矩形空間稱為填充區域。對每個新打開的箱子，集合S默認擁有一個面積為H×W的填充區域s00∈s0，隨著填充操作的持續進行，會有分裂出來的剩余子空間集不斷加入集合S。當或S集合元素無利用價值，即任意 sij都無法容納任意的 ai時，一個箱子的填充操作結束，允許打開新箱繼續填充。每次的填充操作都選擇一個填充區域和若干物品，將物品沿空間寬度W方向按照 hi從高到低的原則依次排列填充，填充操作完畢后將生成子空間集(如圖1所示)，對空間 s00進行填充后，生成包含4個子空間的集合

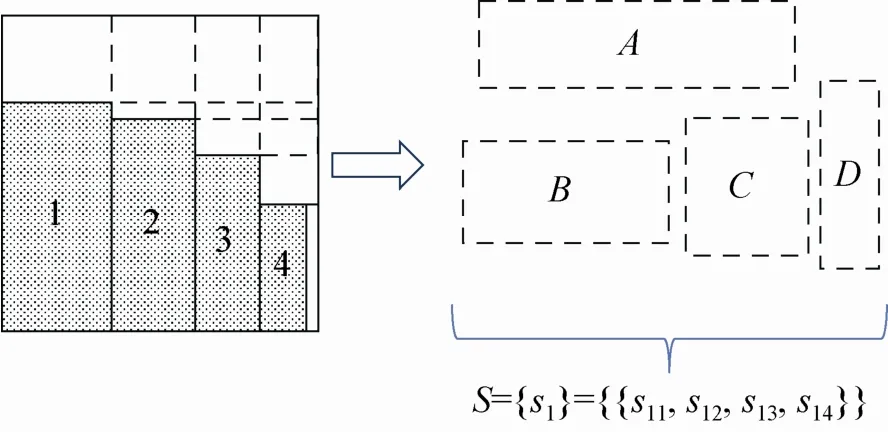
圖1　填充操作后剩余子空間的生成

算法2. pack(r,B)

1.2.1空間的選擇(sele_area(S))

填充操作每次只針對一個矩形區域空間，對新打開的箱子，默認只有一個面積為H×W的填充區域，無需進行選擇。當對某個填充區域進行階梯狀填充操作之后，在每個物品上方均一對一生成小的矩形區域空間sij左下角坐標與物品左上角坐標重疊，右上角坐標與當前填充區域右上角坐標重疊，因此下一輪的填充操作必須進行空間選擇。在如圖 1所示的首輪填充操作后，物品1(2、3、4)對應區域空間A(B、C、D)，4個區域空間形成空間集合S中的一個子集，即各區域空間尺寸、面積各有差異。本文算法按照面積從大到小進行空間選擇，每個空間子集 si只選擇一個空間成為填充區域。如圖1所示的空間子集 s1，優先選擇面積最大的區域 A進行下一輪的物品填充。如果區域 A由于形狀的緣故無法容納候選物品集合中的任何物品，則選擇面積次大的區域 B進行下一輪的物品填充，以此類推，按面積大小進行填充區域選擇。如果所有空間均無法容納物品，且無法與其他區域合并空間，則在集合S中刪除該子集 s1j。

算法3. sele_area(S)

1.2.2物品的選擇(selete(ai,r))

在進行填充操作時，首要步驟是從候選物品集合中挑選合適的物品形成B集合，用于填充當前的面積為H×W的矩形區域，使得填充區域價值最大，然后再考慮剩余空間的利用。此時，物品的挑選實際上是一個經典的0-1背包問題。0-1背包問題描述如下：有n件物品和一個容量為V的背包，第i件物品的重量是 c[i]，價值是w[i]，求解將哪些物品裝入背包可使這些物品的重量總和不超過背包容量，且價值總和最大。0-1背包問題可以用遞歸法、動態規劃法、貪心法和分支界限法等多種方法解決，本文選用動態規劃法。動態規劃的指導思想是先要有效地找出子問題，并通過其子問題推出原問題的解，通常子問題與原問題是相同的，只是規模上的縮小，直到遇見問題的界限。對于0-1背包問題，也可以找出滿足動態規劃的子問題：如果不放第i件物品，那么問題就轉化為“前i?1件物品放入容量為v的背包中”，價值為如果放第i件物品，那么問題就轉化為“前i?1件物品放入剩下的容量為v?c［i］的背包中”。此時能獲得的最大價值就是再加上通過放入第i件物品獲得的價值因此狀態轉移方程為：

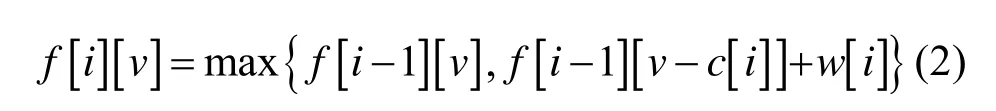
在進行如圖 1所示的物品填充時，由于只允許正交方式擺放，不允許重疊，且物品上下兩個方向均無其他物品，因此可看成一次沿著填充區域的寬度方向的一維填充操作。此時物品的選擇過程就與經典0-1背包問題存在一一對應關系：

(1) 填充區域的寬度W——一個容量為 V的背包；

(2) 物品價值 vi——物品價值w[i]；

(3) 物品寬度wi——物品的重量是 c[i](OG方式)；

(4) 物品寬度wi或長度hi——物品的重量是c[i](RG方式)。

在物品選擇過程中，對于OG方式，只能正放不能倒放，因此，凡是物品過大放不進指定區域即滿足的物品自然淘汰，不在選擇范圍內；而對于RG方式，則需要從正放和倒放兩個方向進行考慮，是選擇物品寬度wi(正放)，還是選擇長度 hi(倒放)作為沿填充區域寬度W填充的對象，主要依據以下判斷規則：

(1) 如果該物品寬度小于等于高度且正放倒放均能放進區域內即wi≤hi&&wi≤W&&wi≤H&&hi≤W&&hi≤H，則選擇物品寬度wi；

(3) 如果該物品寬度大于高度且正放倒放均能放進區域內即wi＞hi&&wi≤W&&wi≤H&&hi≤W&&hi≤H，則選擇物品高度hi；

(5) 其他情況的物品屬于無論正放還是倒放都超出區域的情況，做淘汰處理，不參與物品選擇。

算法4. selete(ai,r)

1.2.3子空間的生成

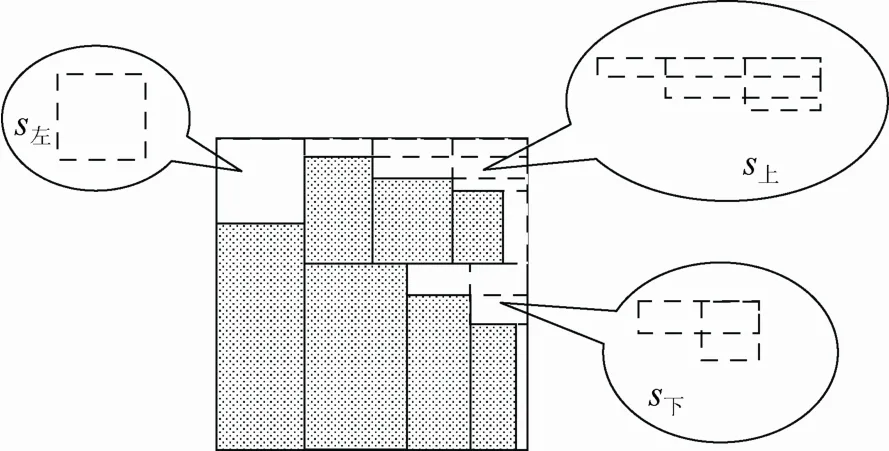
圖2　3個子空間集s上　、s左　和s下的生成

當子空間集均不為空時，添加到空間集S的末尾成為候選空間。如此循環，處理剩余空間。為防止無效空間集的循環生成，設置終止條件：當某個子空間集中所有矩形區域均屬于無效空間時，禁止生成下級空間集并刪除當空間集S=φ時，表示當前箱子已完成填充操作，允許打開新的箱子繼續填充。

剩余空間離散化意味著可選擇的物品種類會變少，因此有必要進行空間擴張或空間融合，這有利于提高空間利用率。當然，采取措施的前提是保證剪切方式的正確實施，因此在做騰挪操作時，應以對應物品的填充寬度作為移動步長。當某個子空間集被定義為無效空間集時，允許其向剩余的相鄰空間集輸送空間。輸送的次序依照空間集S的次序，假設當前空間集如圖3(a)所示。當空間集因無合適物品而被定義為無效空間集時，依照順序，需向右騰挪后被安排給空間集如圖3(b)所示；然后再向上騰挪后被安排給空間集，如圖3(c)所示；當與空間集相鄰的空間集個數為0時，刪除空間集的所有信息。

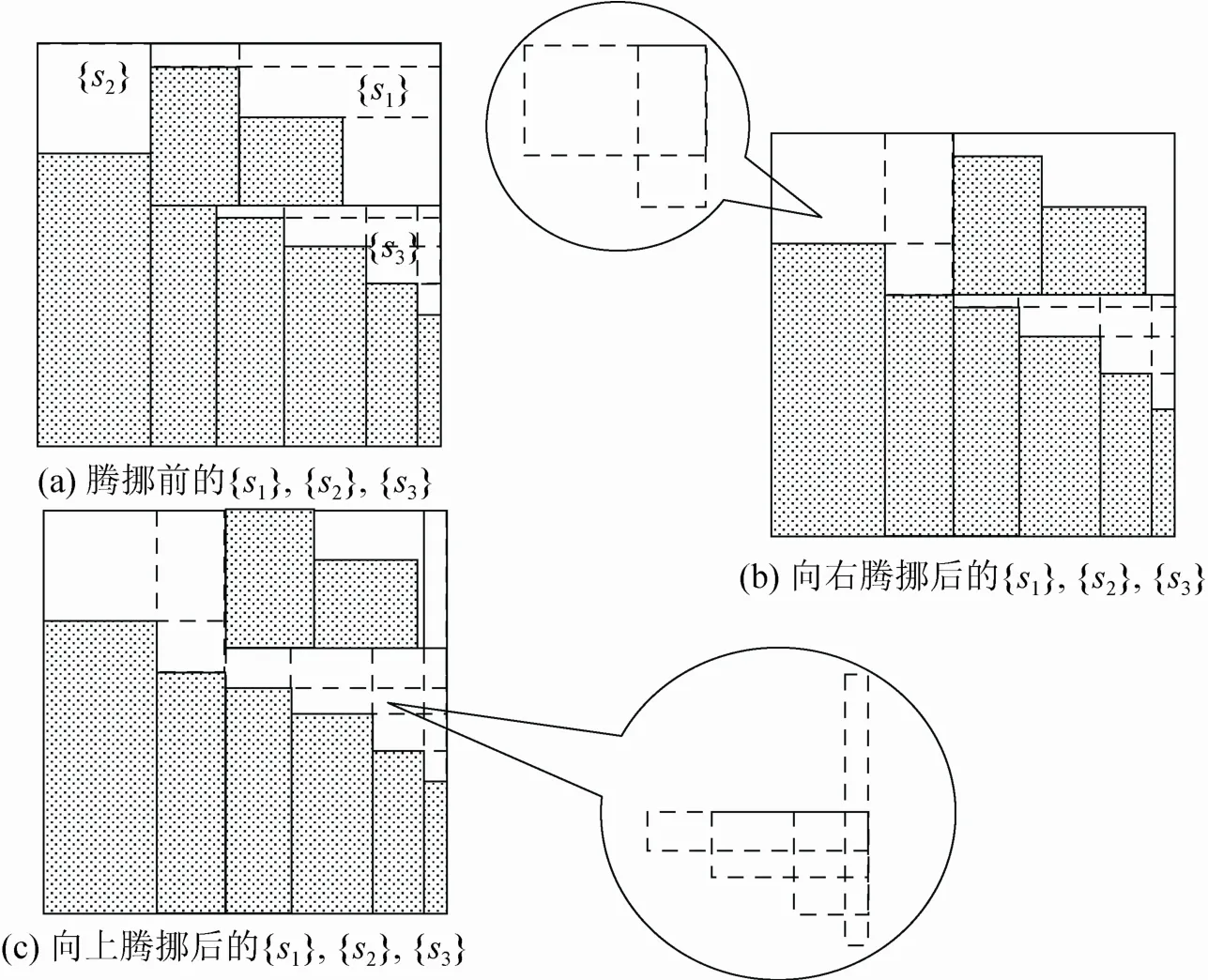
圖3　空間合并示例

1.3價值修正

物品的價值決定了物品在裝箱過程中的優先級別，對于面積較大的，或形狀獨特的，或大部分剩余空間均難以將之容納的物品應賦予更高的價值，提升其優先級別。

本文算法通過多次迭代提高解的質量，每次迭代均根據上一次的裝箱方案C對各物品價值 vi進行修正，以達到讓難裝的物品先行填充的目的。設：在當次迭代產生的裝箱方案C中，物品 ai所在的那個箱子一共填充了m個物品，則面積利用率設置兩個常數g∈(0,1)和 ρ＞1，g為修正價值的權值系數；ρ為控制參數，實驗中可嘗試不同的值使得物品的價值更趨向于合理。本文設計價值修正公式為：

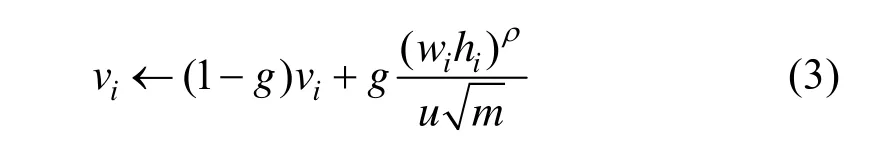
式(3)中，通過權值系數g來調節物品的原價值在新價值中所占的比例；存在的意義在于：箱子中物品個數越多，意味著小尺寸物品較多，且易于和其他物品形成互補關系提升填充率，應該降低該類物品的價值。

通過上述價值公式的修正，使得算法在構造一個解決方案時充分考慮了每個物品的使用頻率，每次迭代生成的裝箱方案都參考了上一次方案的參數，根據參數重新修正物品價值。不再單純以面積利用率作為衡量裝箱效果的唯一標準，而是以箱子物品的總價值作為裝箱優劣的判斷準則，這種修正機制賦予了難裝物品更高的優先權，有效避免了較差方案的生成。

2　實驗結果

本文算法(value correction heuristic，VCH)采用二維裝箱實驗中常用的500個標準算例進行驗算，并與其他算法結果進行比較。500個算例共分為10個classes，每個class包含50個小題。每個小題提供的箱子均為正方形，物品尺寸在小于箱子尺寸范圍內隨機生成，算法采用C#編程，Microsoft visualstudio 2010進行編譯。為了節約運行時間，本文算法讀取了二維裝箱算法下界(lower bound，LB)數據，其中，2BP|O|G 調用了 Fekete和Schepers[5]給出的下界，2BP|R|G調用了Clautiaux等[6]給出的下界。實驗中設置g=0.45;ρ=1.2，經200次迭代計算上述500個標準算例，SH算法取得數據為：2BP|O|G共需7 309個箱子，平均用時0.236 s；2BP|R|G共需 7 059個箱子，平均用時0.255 s。表1顯示本文算法(VCH)與其他啟發式算法進行比較的結果，數據顯示VCH算法在箱子消耗總數上占有優勢。

表2顯示了A-B，CHBP，CFIH+J4算法和本文算法(VCH)的細節數據的對比，同時列出下界(LB)數據作參考。數據表明VCH算法在第5組中表現特別優秀，其他組也取得不錯的結果，無論是O|G方式還是R|G方式，500題的箱子消耗總數比其他算法都要少。

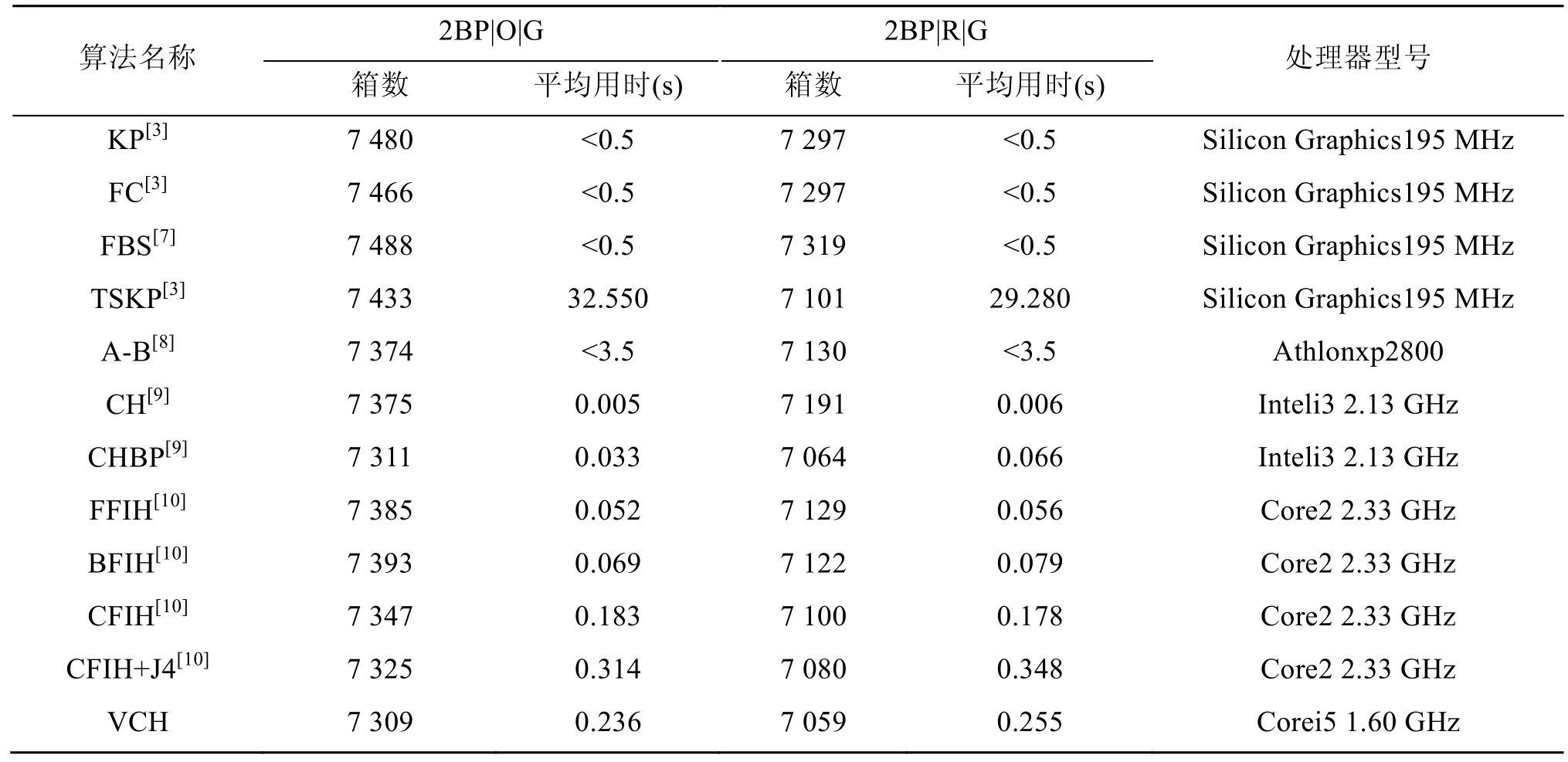
表1　本文算法與其他算法的性能對比數據

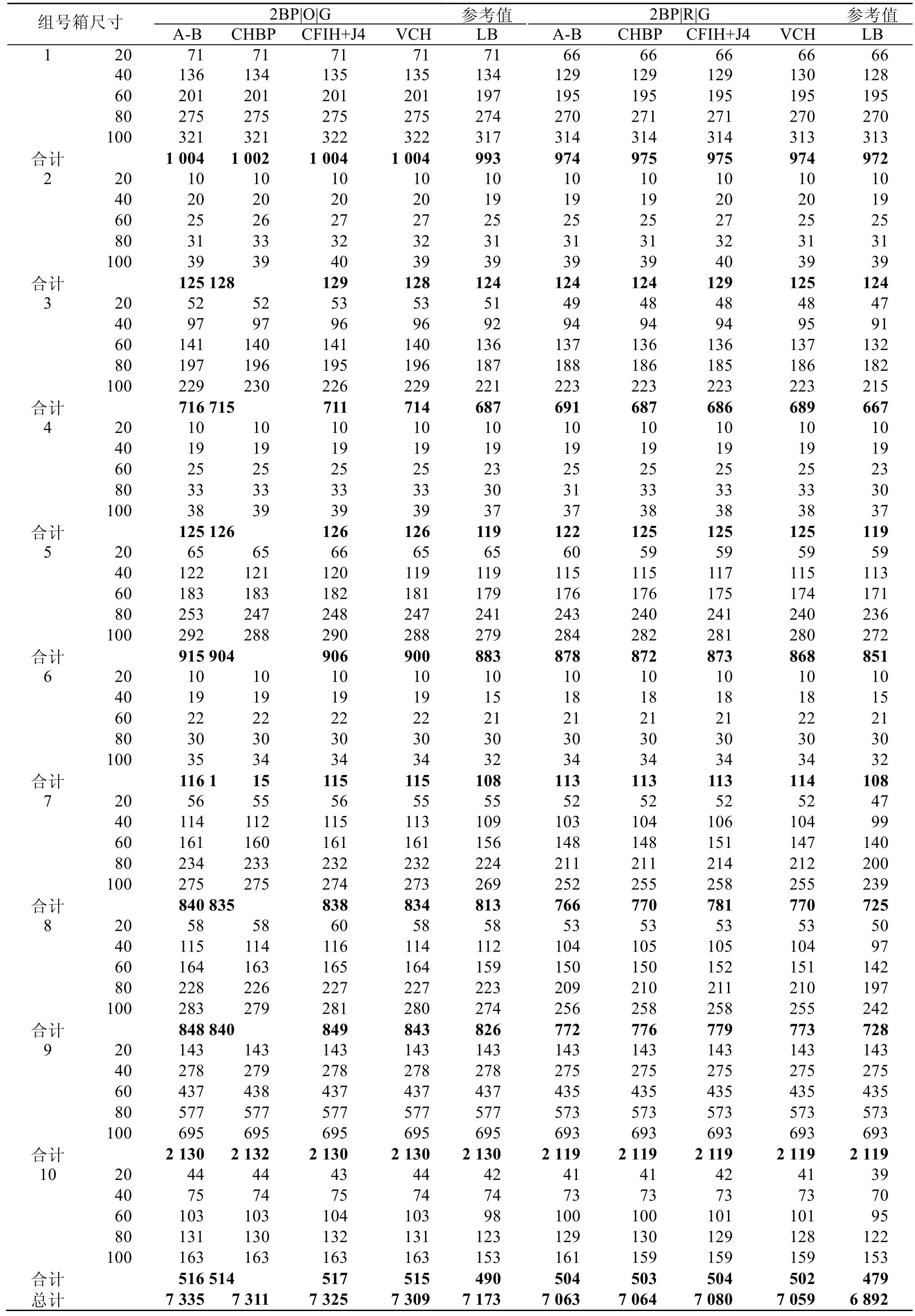
表2　4種算法的分段數據對比(箱子個數)

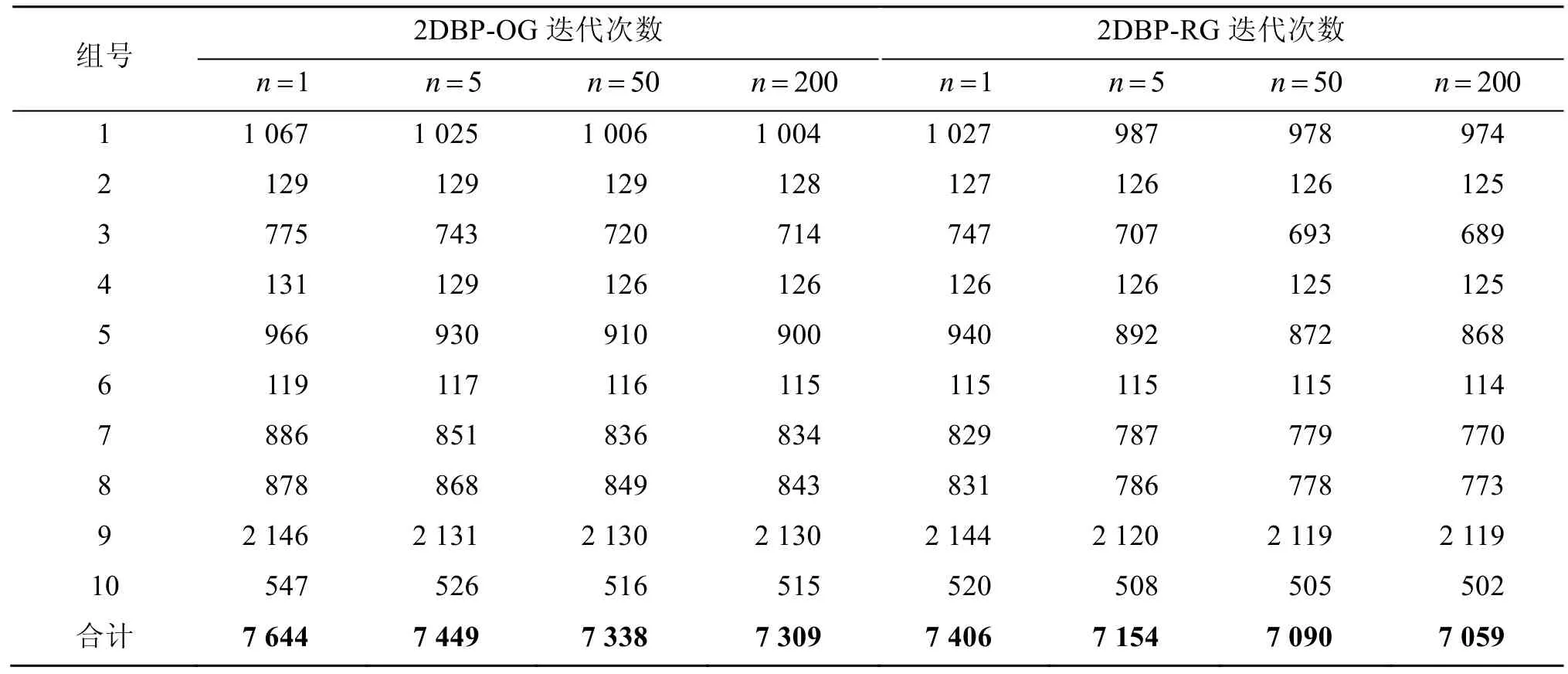
表3　取不同迭代次數的運算結果(箱子個數)

3　結 束 語

本文提出了一個應用于剪切方式的啟發式二維裝箱算法，對當前剩余空間設計了有效劃分和填充，相鄰小空間的合并有效提高了面積利用率。該算法通過修正物品價值調整物品的填充次序，多次迭代使解逐步趨優。實驗表明，相比其他啟發式算法，本文算法取得了較好的裝箱結果。由于其需要多次調用0-1背包子算法，因此耗費時間較多，在時間性能上沒取得更好的結果。基于這個問題，未來可采用并行編程技術，或時間復雜度更低的背包算法，提高時間效率。

[1] 潘衛平, 陳秋蓮, 崔耀東, 等. 基于勻質條帶的矩形件最優三塊布局算法[J]. 圖學學報, 2015, 36(1): 7-11.

[2] 易向陽, 潘衛平, 張俊暉. 基于五塊模式的單一矩形件排樣算法[J]. 圖學學報, 2015, 36(4): 521-525.

[3] Lodi A, Martello S, Vigo D. Heuristic and metaheuristic approaches for a class of two-dimensional bin packing problems [J]. INFORMS Journal on Computing, 1999, 11(4): 345-357.

[4] W?scher G, Hau?ner H, Schumann H. An improved typology of cutting and packing problems [J]. European Journal of Operational Research, 2007, 183(3): 1109-1130.

[5] Fekete S P, Schepers J. A general framework for bounds for higher dimensional orthogonal packing problems [J]. Mathematical Methods of Operations Research, 2004, 60(2): 311-329.

[6] Clautiaux F, Jouglet A, Hayek J E. A new lower bound for the non-oriented two-dimensional bin-packing problem [J]. Operations Research Letters, 2007, 35(3): 365-373.

[7] Lodi A, Martello S, Vigo D. Recent advances on two-dimensional bin packing problems [J]. Discrete Applied Mathematics, 2002, 123(1-3): 296-379.

[8] Polyakovsky S, M′Hallah R. An agent-based approach to the two-dimensional guillotine bin packing problem [J]. European Journal of Operational Research, 2009, 192(3): 767-781.

[9] Charalambous C, Fleszar K. A constructive bin-oriented heuristic for the two-dimensional bin packing problem with guillotine cuts [J]. Computers & Operations Research, 2011, 38(10): 1443-1451.

[10] Fleszar K. Three insertion heuristics and a justification improvement heuristic for two-dimensional bin packing with guillotine cuts [J]. Computers & Operations Research, 2013, 40(1): 463-474.

[11] Belov G, Scheithauer G. Setup and open-stacks minimization in one-dimensional stock cutting [J]. INFORMS Journal on Computing, 2007, 19(1): 27-35.

[12] Belov G, Scheithauer G, Mukhacheva E A. One-dimensional heuristics adapted for two-dimensional rectangular strip packing [J]. Journal of the Operational Research Society, 2008, 59: 823-832.

A Heuristic Algorithm for Two-Dimensional Bin Packing with Guillotine Constraints

Yao Yi1,2,Lai Chaoan1
(1. School of Business Administration, South China University of Technology, Guangzhou Guangdong 510640, China; 2. College of Computer and Electronics Information, Guangxi University, Nanning Guangxi 530004, China)

A heuristic approach for two-dimensional bin packing problems with guillotine constraints is proposed to minimize bin usage by maximizing space efficiency through the strategy of value correction. This heuristic algorithm firstly assigns higher values and packing priorities to items considered more difficult to pack into residual spaces, then selects packing spaces in descending order of unused area, and finally expand or merge residual small spaces and add unusable space to the residual adjacent space set, so as to improve the utilization rate. Simulation experiments on benchmark test sets suggest that the approach can work effectively and rivals existing other 2DBP methods.

two-dimensional bin packing; value correction; guillotine cut; heuristic

TP 391

A

2095-302X(2015)06-0879-08

2015-06-25；定稿日期：2015-07-08

國家自然科學基金面上項目(71371058)；國家自然科學基金地區科學基金項目(61363026)

姚怡(1975–)，女，廣東陽江人，副教授，碩士。主要研究方向為組合優化算法。E-mail：yaoyi@gxu.edu.cn

賴朝安(1973–)，男，廣西欽州人，副教授，博士。主要研究方向為制造信息化、創新方法。E-mail：chalai@scut.edu.cn