基于力學矢量加法的二維PAR過程及其實證研究

張 昴

(中國政法大學商學院，北京 102200)

金融時間序列分析在探索經濟規律中發揮著越來越重要的作用。ARMA過程作為經典的時間序列分析方法較好地反映了時間序列的線性特征。然而現實中許多時間序列往往隱含有高度的非線性特征，它們的變化受到許多復雜因素的綜合作用，這正是ARMA過程在實際應用中真正需要解決的問題。

目前，從統計學角度出發已構建了一系列非線性計量模型。Granger和 Anderson［1］提出了雙線性時間序列模型，給出了耦合的交叉項，邁出了非線性計量的重要一步。Granger［2］在研究ARMA模型時提出分數階的差分，對非平穩時間序列自相關問題進行處理，得到了較好的效果。Haggan和Ozalci［3］突破傳統建模的正態分布假定提出了指數自回歸(EXPAR)模型，為非線性計量分析提供了一個新方向。Chen和 Tsay［4］提出了變系數自回歸(FAR)模型，其泛化能力較強，較好地刻畫了時間序列的演變規律。人們也嘗試用幾何分形理論對經濟系統進行研究，Edgar E.Peters［5］將分形幾何學理論引入資本市場的分析，為此后分形幾何學和混沌動力學的迅速發展作了重要鋪墊。20世紀，憑借軟計算方法對不確定、不精確問題的較好適應性，學術界掀起了一股軟計算方法研究的潮流。Lapedes和Farbar［6］開創性地運用人工神經網絡對股票價格進行分析建模，較好地刻畫了股票價格的復雜性、耦合性。近年來，人們不斷嘗試多種軟計算方法的組合預測。Li C和Cheng H H［7］提出PSO-RLSE與模糊控制論相結合的軟算法，對SP500序列進行分析，從而證明其提出的混合計算方法的優越性。張旭東等［8］將小波與神經網絡相結合對深證300成分指數進行預測。Lahmiri S［9］創新性地采用離散小波技術和支持向量機對SP500股票價格變動方向進行預測，得到了較為準確的結果。

復雜系統的研究已經成為當今學術趨勢，尤其是交叉學科的研究思路和方法已經漸漸得到廣泛的應用。閆妍等［10］介紹了交叉相關矩陣、復雜網絡等統計物理方法在全球股市價格波動上的應用。借鑒物理中關于復雜系統的研究思路和方法，本文以經典物理學矢量的非線性加法為依托解讀經濟系統的非線性，創建二維矢量形式的AR過程(phasor auto regressive model，PAR)，并對其進行實證研究。

1 PAR過程的構建

1.1 傳統AR過程的不足以及經濟系統的非線性根源

時間序列分析中常用的AR過程的一般形式為rt－ φ1rt－1－ …－ φprt－p=et，這是一個線性加法形式的方程。然而現實經濟系統中的許多經濟指標通常既存在線性特征又存在非線性特征。以股票收益率序列為例，對其直接建立的線性AR過程并不能捕捉非線性部分的信息，此時模型的估計是有偏的，因此必然會帶來有效信息的損失。

經濟系統中的非線性根源是各種因素綜合作用于經濟指標。本文用經典物理學的力學理論來闡述經濟指標受到的諸多因素:一個方向上的力對應一種作用因素，一個經濟學指標的實現受到了多種大小和不同方向力的作用。這是對經濟系統中經濟指標非線性根源的力學解讀。經典物理學中力是按照矢量加法的平行四邊形法則進行運算的，受力作用的物理指標同樣要按照矢量法則進行運算。物理上的矢量法則的數學特征形式表現為不是按照線性疊加原理進行的，即 f(aφ+bψ)≠af(φ)+bf(ψ)。受多種因素綜合作用的經濟系統中，經濟指標呈現不按正比例變化的特征，因此經濟指標的加法就不是線性法則，同樣要按照矢量法則進行運算。

1.2 非線性的矢量加法法則

平行四邊形OA1A3A2中，矢量加法的平行四邊形法則為OA3=OA1+OA2，如圖1所示。

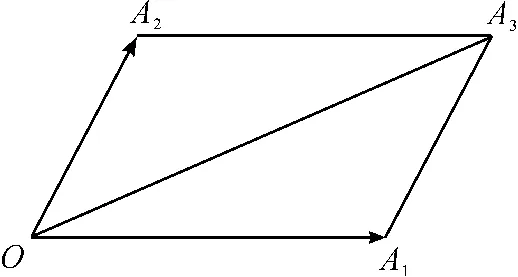
圖1 矢量的平行四邊形加法法則

可以看出兩個指標的矢量和OA3落在以OA1與為OA2為鄰邊的平行四邊形OA1A3A2的對角線上，它由大小和方向兩個要素唯一確定。注意到，OA3的大小并不等于OA1和OA2的大小直接相加的結果，即這是一種非線性的加法，OA3會根據OA1，OA2的大小和方向做出適應性調整，這樣矢量的加法就可以適應數據結構的形態，進而捕捉到數據內部的非線性特征。

1.3 經濟學用矢量做非線性加法的重要意義

在矢量分析中經濟指標OAi(i=1，2，3)有大小和方向兩個維度，這樣就能更好地體現經濟指標大小的不確定性和方向的復雜性。二維視角下第t期經濟指標OAt可以看作是第t－1期經濟指標 OAt－1、第 t－2 期經濟指標 OAt－2，…，第 t－p 期經濟指標OAt－p的矢量組合，而不是傳統的線性加法組合(φ1rt－1+… + φprt－p)。從經典物理學中力學矢量合成的角度來看，第t期經濟指標在多種因素作用下的實現可以看作是 OAt－1，OAt－2，…，OAt－p對應因素的實現。由于 OAt會根據 OAt－1，OAt－2，…，OAt－p的大小和方向做出適應性調整，這樣指標加法法則就可以捕捉到經濟序列的非線性特征。

1.4 PAR過程及其圖解

基于將矢量加法法則應用于非線性過程的合理性，本文把影響經濟指標rt的各種因素對應于物理學上不同大小、不同方向的力，把受多種作用力影響的經濟指標在二維平面上進行矢量疊加，進而提出同時具有大小和方向的二維矢量形式AR 過程:rt－ φ1rt－1－ …－ φprt－p=et。矢量方程等號兩邊矢量大小一致，方向相同。如圖2所示，其中ORt是有大小和方向的經濟指標序列，ON是服從二維正態分布的白噪聲。二維白噪聲豐富地再現了經濟系統的噪聲信息沖擊，凸顯了經濟指標波動的復雜性。

圖2 PAR過程圖解

PAR 過程 rt－φ1rt－1－…－φprt－p=et是一個矢量方程，它表明第t期經濟指標rt可以看作是第t－1 期經濟指標 rt－1，第 t－2 期經濟指標 rt－2，…，第t－p期經濟指標rt－p的矢量組合。rt的大小和方向根據此矢量組合進行適應性調整。

經典物理學上對矢量過程分析的方法是正交分解變換。正交分解變換的一般步驟:首先按照力學上化曲為直的等效替代思想，對多因素、多作用力的非線性運動做正交化分解;然后計算水平方向、豎直方向正交分量的線性運動;最后再根據矢量加法法則合成曲線運動。

2 PAR過程在二維平面的運算

2.1 PAR過程的坐標方程

為了平面直角坐標系中運算方便，把指標數據映射到［0，1］區間內進行標準化。同時為了確定指標rt在二維平面中的方向，將指標rt按照大小沿ORt方向從最低點O出發畫在直徑d為1的圓中，對應得出唯一的矢量ORt(正值數據刻畫在第1象限和負值數據刻畫在第3象限)。當然，也可以把經濟指標畫在橢圓或者其他平面幾何中，選擇圓作為分析框架是因為圓具有更好的中心對稱性和軸對稱性，并且在圓中坐標的表示及三角函數運算比較簡單。

需要指出的是當且僅當在45°角的情況下，作用力的水平分量和豎直分量才會相等，此時作用力在兩個正交方向才能同時有效地發揮作用，這是力作用效果最大化的體現，也是作用效果的極大值點。于是序列中的最大數據rmax在圓中應該映射為

由于經濟指標序列的最小值不能標準化為0(此時沒有力的作用)，因此采用正比例形式的最大值標準化方法。此時，對應的數據標準化公式為基于此下面推導將指標標準化到區間后的二維坐標形式。

在圓里面，取直徑OO'為1，記任意一條弦OR的弦切角(與水平線正方向的夾角)為α，如圖3所示。

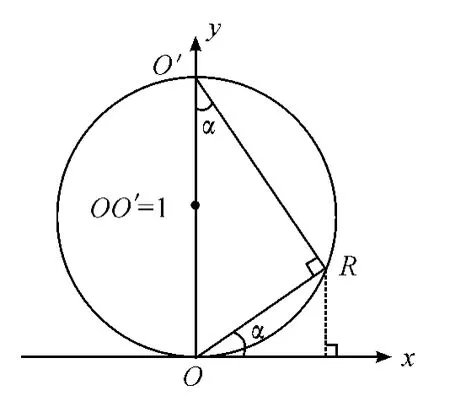
圖3 經濟指標rt的二維正交分解

根據弦切角定理，在圓上弦所對的圓周角等于弦切角，于是有∠OO'R=α。在直角△OO'R中，OO'=1，進而得出通過上述推導得出如下結論:在直徑為1的圓中任意圓周角α對應弦的弦長為sinα。此時R點在水平方向、豎直方向的正投影分別為sinαcosα，sinαsinα，于是 R點的坐標可表示為(sinαcosα，sinαsinα)［11］。因－π/2＜α＜π/2，而負值數據刻畫在第3象限，其坐標仍然表示為(sinαcosα，－sinαsinα)。為了統一，本文采用，這樣坐標在兩個象限的表示是一致的。

反過來對于標準化后的時間序列{rt}，相當于已知弦 OR的弦長為rt，求其弦切角為αt=arcsinrt，再用αt表示R點坐標。以標準化后的股票收益率序列{rt}為例，平面直角坐標系中，ORt是第t個交易日的股票收益率，大小為rt，對應的弦切角為αt=arcsinrt，坐標形式為(sinαtcosαt，

把標準化收益率序列{rt}中數據都在平面直角坐標系中進行正交分解，就得到了二維形式的矢量收益率序列(xt，yt)，標準化收益率和二維形式的收益率序列(xt，yt)的關系為

這樣PAR過程在二維平面就可以表示為:

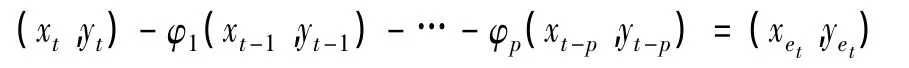
2.2 PAR方程的系數計算辦法

本文采用離差平方和的最小二乘法方法做PAR回歸方程的系數估計。

實際測量值rt與回歸值之間存在著偏差，稱為殘差，記作 ei(i=1，2，3，…，n)。PAR 回歸方程的殘差由兩個分量序列的殘差構成:

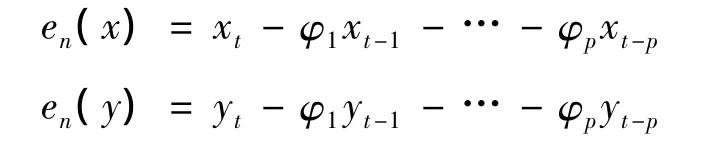
相應的二維形式PAR回歸方程的殘差平方和為

最小二乘法就是尋找系數φ1，…，φp的最佳估計值，使得離差平方和最小。由于Q是關于的二次函數，微積分學上二次函數的極小值總是存在的，因此根據微積分中求函數極值的原理，使Q對求偏導數，偏導數值為0時離差平方和Q即可達到最小。于是有:

線性方程組的解是唯一存在的，把兩個分量序列數據帶入上面的線性方程組，在Excel中進行運算，即可求得PAR過程滯后p階的各項系數。

3 實證研究

3.1 數據的選取與處理

為了證明PAR過程在刻畫時間序列非線性特征的有效性和精確性，本研究選取比較成熟的美國股票市場指數SP500每交易日的股票收盤價格序列{pn}進行分析。價格序列的時間段為2010年10月1日至2015年2月17日，利用公式rn=lnpn－lnpn－1計算得出1 100個對數收益率數據。選用前1 000個樣本數據作為訓練集，后100個樣本數據作為驗證集。數據來源于Yahoo Finance，利用Eviews8.0和Excel2010對數據進行檢驗和分析。

基于圓中45°弦對應序列中最大數據的特性，我們將收益率序列映射到區間內。設時間序列{rn}中的最大值為rmax，則歸一化后的數據對r'正交分解得到矢量收益率的兩個分量序列{rx}和{ry}。

接下來本文對時間序列{rn}，{rx}和{ry}進行分析預測。

3.2 收益率序列平穩性檢驗

為檢驗收益率序列{rn}以及矢量收益率序列兩個正交維度分量序列{rx}和{ry}的平穩性，使用帶截距項和趨勢項的ADF單位根檢驗對3個序列進行平穩性檢驗，檢驗結果如表1所示。

表1 3個序列的平穩性檢驗結果

從表1可以看出，3個序列ADF檢驗的p值在5%的臨界水平下均顯著，因此收益率序列均通過ADF檢驗，此時應當拒絕序列不平穩的假設，認為3個序列都是平穩的，符合AR過程分析的基本條件。

3.3 收益率傳統AR過程定階及系數輸出

根據Box和Jenkins所提出的AR模型建立方案。觀察序列{rn}的偏自相關函數值，發現該序列在AR(3)和AR(5)顯著。模型相應參數的輸出如表2所示。

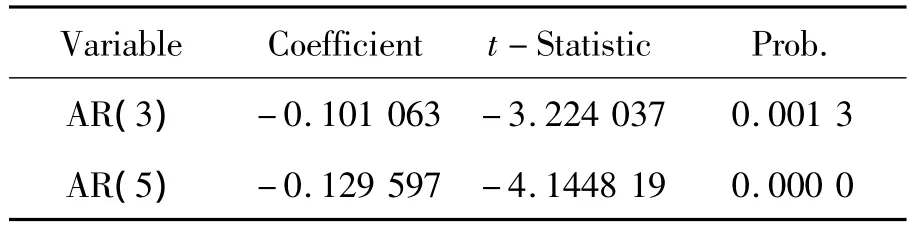
表2 {rn}序列AR(3)和AR(5)系數的t檢驗結果

3.4 收益率PAR過程定階及系數計算

PAR過程要求{rx}和{ry}兩個分量序列建立相同的滯后項及系數。比較{rx}，{ry}的偏自相關函數值，發現兩序列在AR(3)和AR(5)兩期滯后項顯著，其相應的顯著性t檢驗結果如表3和表4所示。

表3 {rx}序列AR(3)和AR(5)系數的t檢驗結果

表4 {ry}序列AR(3)和AR(5)系數的t檢驗結果

因此確立PAR(3)和PAR(5)過程如下:

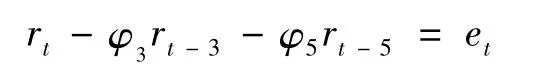
此模型的坐標方程可表示為

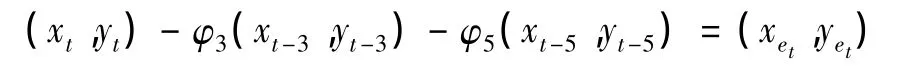
下面用最小二乘法求出系數φ3，φ5的值，此時PAR回歸方程的離差平方和為

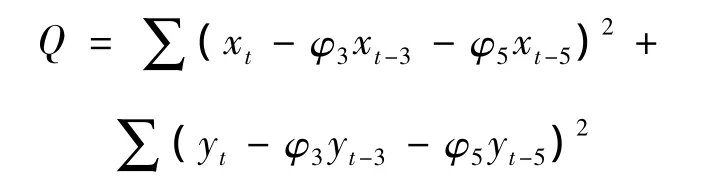
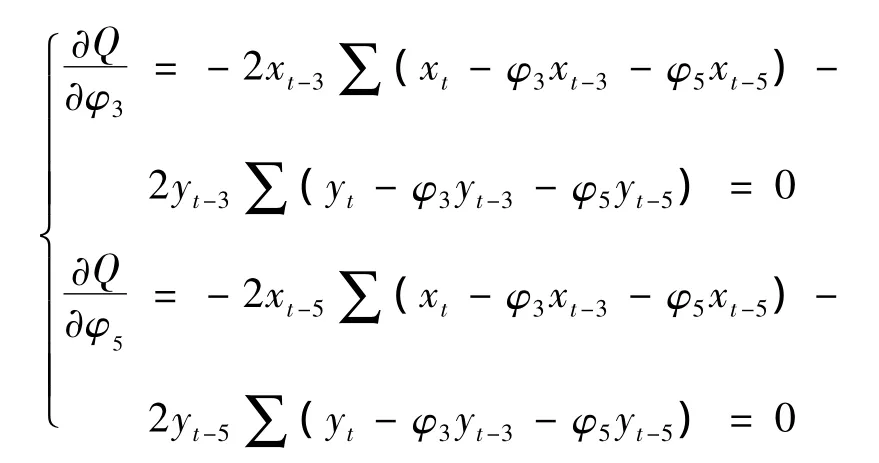
解方程可得PAR過程的系數。下面給出一步靜態預測示例。用Excel計算前1 000個收益率樣本數據、求得的AR(3)和AR(5)系數及其一步收益率(2014年9月24日)預測，如表5所示。

表5 前1 000個樣本數據建立的PAR過程及其一步預測

3.5 預測與評價

用最小二乘法對SP500收益率序列逐步進行100步靜態預測進而還原價格序列。本文參照文獻［12］關于時間序列預測的5個常用指標對預測值進行評價。

平均預測誤差平方和的平方根(RMSE):

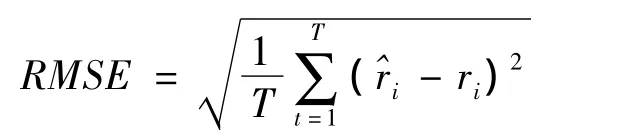
Theil不相等系數(U):

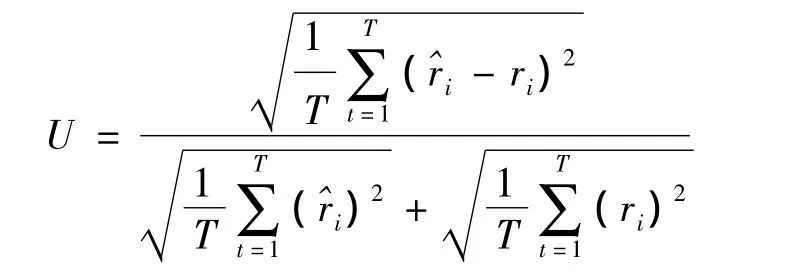
平均絕對誤差(MAE):

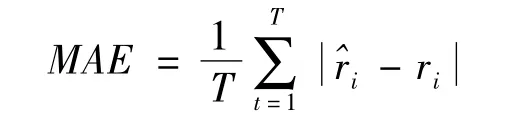
平均預測誤差(MFE):

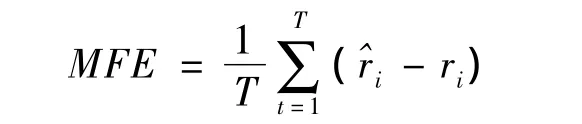
平均絕對百分比誤差(MAPE):

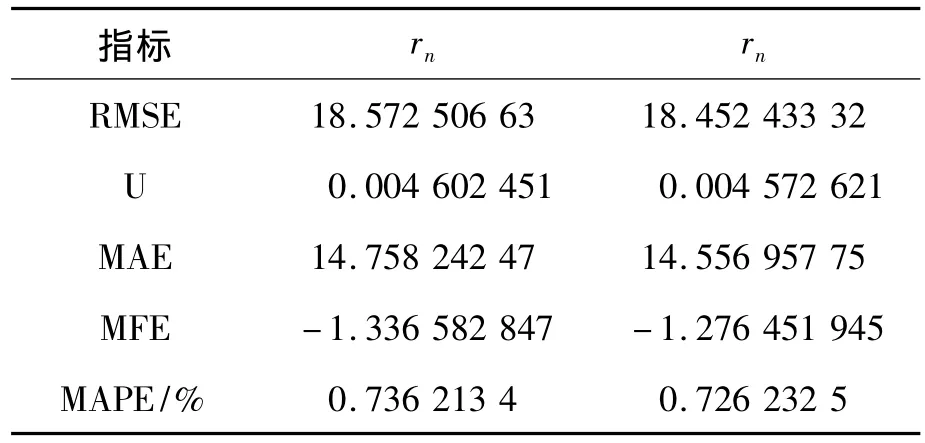
表6 序列{rn}和序列{rn}預測的誤差結果

從預測結果可以看出:本文提出的收益率序列的PAR過程與收益率序列直接建立的AR過程相比，在對SP500收益率序列(2010年10月1日至2014年9月23日)進行建模預測時，5種指標評價誤差均較低，預測準確度相對較高，優勢明顯。

3.6 結果分析

對收益率構建的傳統AR過程和PAR過程都建立了AR(3)和AR(5)兩期滯后模型，其中PAR過程的預測精度更高。一方面PAR過程把不同大小、不同方向作用力和作用于經濟系統中經濟指標的各種因素對應起來，用經典物理學的力學理論展現了經濟指標受到的各種復雜作用因素，挖掘到了經濟系統中經濟指標的非線性根源。另一方面PAR過程對經濟指標的非線性矢量加法運算和二維平面上有方向的白噪聲信息沖擊豐富地再現了經濟系統的復雜性，有力地克服了傳統AR過程不能刻畫經濟系統中由多因素造成的非線性特征的缺陷，較好保留了經濟系統的非線性信息，適應了經濟系統的復雜性發展規律。

4 結束語

現實經濟系統中的時間序列由于受到許多復雜因素的影響和作用往往呈現出一些非線性的特征，所以對時間序列建立的傳統線性AR模型就不能捕捉經濟指標的非線性信息。本研究用經典物理學中矢量的加法法則為基礎解讀經濟系統的非線性，創立時間序列的矢量分析法，并與AR過程相結合，開創二維形式的矢量AR過程。在平面直角坐標系中對矢量經濟指標進行正交化分解得到兩個正交分量序列{rx}和{ry}，由此給出了PAR過程在平面直角坐標系中的坐標方程。通過觀察兩個正交分量序列共同顯著的偏自相關函數，構建相應的二維形式PAR方程，進一步用離差平方和的最小二乘法推導出PAR坐標方程的系數。最后，對SP500收益率序列建模時PAR過程和傳統AR過程建立的是兩期相同滯后項的模型，對時間序列{rn}、{rx}和{ry}進行100步靜態預測進而還原得到價格序列，采用 RMSE，U，MAE，MFE，MAPE對預測效果進行評價。結果表明:PAR過程的預測精度顯著高于傳統的AR過程，進一步論證了PAR過程在詮釋經濟系統復雜的非線性特征時的有效性。

［1］Granger C W J，Anderson A.An Introduction to Bilinear Time Series Model［M］.Gottinggen:Vanderhoech and Ruprecht，1978.

［2］Granger.Long-memory Tine Series Models and Fractional Differencing［J］.Journal of Time Series Analysis，1980(1):15－29.

［3］Haggan V，Ozaki T.Modeling nonlinear vibrations using an amplitude-dependent autoregressive time series model［J］.Biometrika，1981，68:189－196.

［4］Chen R，Tsay R S.On the ergodicity of TAR(l)processes［J］.The Annals of Applied Probability，1991(1):613－634.

［5］Peters E E.Chaos and order in the capital markets:a new view of cycles，prices，and market volatility［M］.［S.l.］:John Wiley ＆ Sons，1996.

［6］Alan S L，Evan W S，Robert M F.Use of Adaptive Networks to Define Highly Predictable Protein Secondary-Structure Classes［J］.Machine Learning，1995，21(1/2):103－124.

［7］Li C，Cheng H.Intelligent forecasting of S＆P 500 time series—A self-organizing fuzzy approach［M］.Intelligent Information and Database Systems.Berlin:Springer Berlin Heidelberg，2011:411－420.

［8］張旭東，俞建寧，郭蘭平，等.基于小波神經網絡的深證300成分指數的預測［J］.重慶理工大學學報:自然科學版，2011(6):49－52.

［9］Lahmiri S.Forecasting direction of the S＆P500 movement using wavelet transform and support vector machines［J］.International Journal of Strategic Decision Sciences(IJSDS)，2013，4(1):79－89.

［10］Yan Y，Mao-Xin L，Xiao-Wu Z，et al.Principle fluctuation modes of the global stock market［J］.Chinese Physics Letters，2012，29(2):028901.

［11］張昴，郭琨.基于等時圓矢量差分的ARVMA模型及其實證研究［J］.系統科學與數學，2015(2):193－205.

［12］惠曉峰，柳鴻生，胡偉，等.基于時間序列GARCH模型的人民幣匯率預測［J］.金融研究，2003(5):99－105.