魚雷被動聲自導反艦深度設定方法

王桂芹，李 偉，鄧 鵬

(海軍潛艇學院 導彈兵器系，山東 青島266042)

0 引 言

由于現代潛艇減振降噪技術的發展，魚雷被動聲自導幾乎只能用于打擊中高速航行的水面艦船目標。被動聲自導系統在搜索目標時，在垂直方向上通常按照設定深度航行。魚雷被動聲自導系統本質上為一部小型聲吶，搜索深度的設定，決定了反艦搜索效能的發揮。目前鮮有魚雷設定深度方面的研究，僅根據部分定性分析或習慣，缺乏定量分析和研究。

被動自導搜索設定深度的研究，前提條件是用于評價搜索效果指標，進而分析影響搜索效果的主要參量。被動自導作用距離是評價自導系統效能的主要指標，主要依據被動自導方程中各項參數進行計算。被動自導方程各項參數中，魚雷自噪聲級和傳播損失隨深度變化。本文將綜合2個要素的仿真分析，進行魚雷被動自導作用距離仿真計算，作為搜索深度設定的依據，研究典型水文條件下搜索深度設定原則。

1 魚雷被動聲自導期望作用距離計算方法

自導期望作用距離是評價魚雷自導系統效能最直接有效的指標，通常采用被動自導方程計算被動自導期望作用距離。

被動自導方程為:

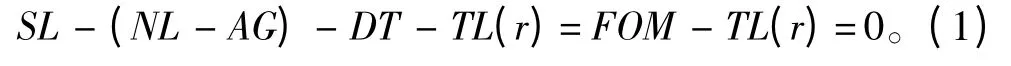
式中:SL為聲源級;NL為噪聲級;AG為自導接收基陣陣列增益;DT為檢測閾;FOM為優質因子;TL為傳播損失。TL為魚雷與目標距離r的函數。當FOM≥TL 時，則魚雷被動自導系統以一定概率發現目標，根據此條件即可計算魚雷被動聲自導期望作用距離r。聲源級SL 衡量艦船目標輻射噪聲，與目標類型、尺寸、航速等因素有關;陣列增益AG 由自導基陣自身參數決定;噪聲級NL 反映自導系統的干擾，魚雷被動自導工作時，干擾包括環境噪聲、魚雷自噪聲和其他反魚雷手段的干擾。魚雷自導系統工作頻率較高，通常在20 kHz左右，在此頻率上，環境噪聲主要為來自海面的風雨噪聲，噪聲譜級僅為30 dB［1］左右，遠小于魚雷自噪聲，因此不考慮反魚雷手段的前提下，被動自導系統干擾主要為魚雷自噪聲。在魚雷航速超過20 kn 時，在自導工作頻率上，魚雷自噪聲主要以螺旋槳空化噪聲為主［2］。螺旋槳空化噪聲經由海水、海底散射或海面散射，傳播到自導基陣形成自噪聲。

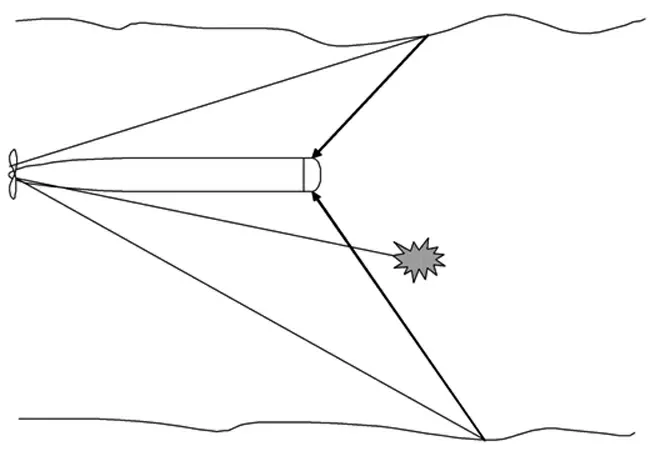
圖1 魚雷自噪聲形成機理Fig.1 Torpedo self-noise formation

魚雷自噪聲包括體積散射噪聲和界面散射噪聲，文獻［3－4］對魚雷自噪聲模型進行研究，但假設條件中認定魚雷接收基陣無指向性，這與實際情況不符合。因此，對其進行修正，體積散射自噪聲NLV和界面散射自噪聲NLS計算模型為:

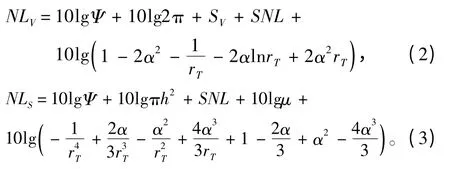
式中:SV為海水體積散射系數(通常為－90 dB～－70 dB)［5］;SNL為魚雷輻射噪聲級;α為海水吸收系數;rT為自噪聲仿真計算距離;h為魚雷距離海面或海底深度，m;μ為界面散射系數，可采用Lambert 定律計算。

式中:μ0為界面散射常量;θ為入射角;φ為散射角。Ψ為反映被動自導系統接收指向性的參數。設魚雷被動波束為理想波束情況，即立體波束角內的接收指向性為1，其余為0，則:

式中:ω為魚雷基陣接收水平波束角寬度;φ為魚雷基陣接收垂直波束角寬度。檢測閾DT為:

其中R0.5為自導檢測概率為0.5 時接收機信噪比門限。魚雷被動自導搜索目標時，尚未發現目標，信號檢測通常采用能量檢測方式。若目標噪聲信號幅值與環境噪聲幅值均服從高斯分布，且被動自導系統為平方－積分處理方式，則自導接收機輸出信號與噪聲幅值服從瑞利分布，根據文獻［6］:

式中:pf為虛警概率;Δf為帶寬;Δt為積分時間;erfc為補償誤差函數;erfc－1為其反函數。

傳播損失TL 由海區水文條件、自導頻率等因素決定。由于魚雷自導工作頻率較高，通常在20 kHz 以上，采用高斯束射線Bellhop模型計算傳播損失TL。根據自導方程各項的仿真計算，將FOM與TL(r)比較，即可計算魚雷設定深度不同時魚雷被動自導反艦期望作用距離，將其作為魚雷深度設定的依據。

2 魚雷被動聲自導反艦深度設定仿真分析

2.1 魚雷自噪聲仿真計算

設海深120 m，海水吸收系數α為6 dB/km，弱不平整海底，海底散射系數μ1為－20 dB，海況3級，海面散射系數μ2為－21 dB，體積散射系數SV為－80 dB，魚雷工作深度h為25 m，聲自導水平波束角±40°，垂直波束角± 12°，魚雷輻射噪聲級SNL為108 dB，則在5～1 000 m的體積散射自噪聲、海面散射自噪聲、海底散射自噪聲和魚雷自噪聲仿真結果如圖2所示。

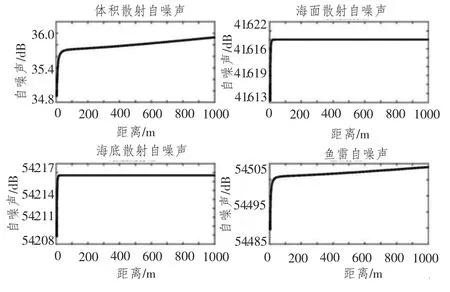
圖2 魚雷自噪聲仿真分析結果Fig.2 Torpedo self-noise simulation and analysis

從圖2 可看出，魚雷自噪聲主要海底和海面散射產生，而體積散射自噪聲可忽略。仿真距離超過10 m 后，魚雷自噪聲趨于穩定。魚雷工作深度取值不同時的仿真也表明，魚雷自噪聲主要為海面和海底散射自噪聲。

下面對魚雷自噪聲隨深度變化進行分析。將魚雷深度在5～115 m 離散取值，自噪聲仿真結果如圖3所示。由圖3 可以看出，魚雷在67 m 深度航行時，自噪聲最低，僅為58.75 dB;魚雷靠近海面或者海底時，由于界面散射的影響，自噪聲較大，在5 m和115 m 時，自噪聲分別達61.91 dB和60.92 dB，超過67 m 深度的自噪聲為2～3 dB，因此，有必要研究自噪聲影響下魚雷被動自導搜索深度如何設定。

2.2 魚雷被動聲自導期望作用距離仿真與分析

設水面艦船等效聲學中心深度為5 m，魚雷自導工作頻率為25 kHz，AG =5 dB，在等聲速、負梯度、正梯度和負躍層4 種典型聲速分布及該條件下的傳播損失分布，以及不同深度下魚雷被動聲自導期望作用距離如圖4～圖7所示。

圖4為等聲速條件下的被動自導作用距離仿真。可以看出，67 m 深度上魚雷自導作用距離最大，可達2.15 km，在靠近海面和海底深度上，自導作用距離僅1.7 km 左右。這是由于在等聲速條件下傳播損失在垂直方向上分布比較均勻，則魚雷被動自導最佳搜索深度主要由自噪聲在垂直方向上的分布決定。67 m 深度同時也是等聲速條件下魚雷自噪聲最小的深度。

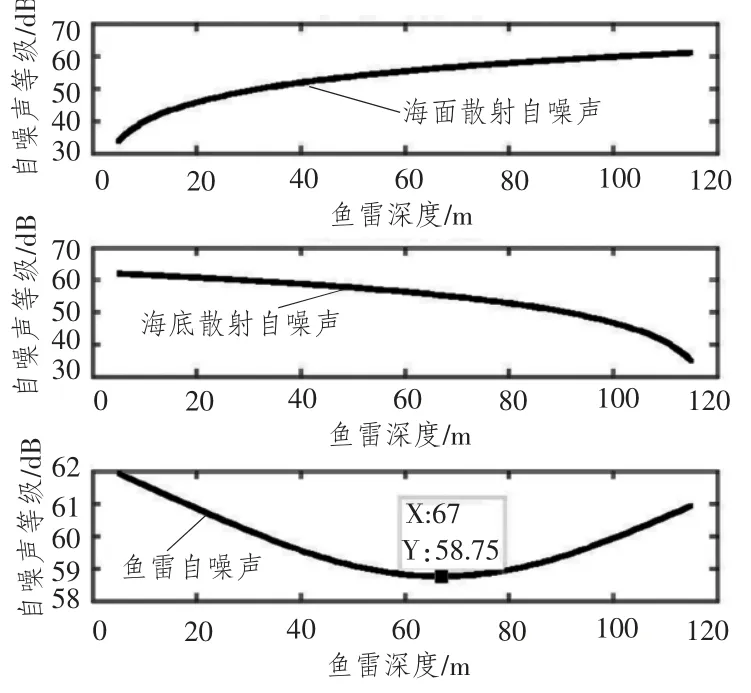
圖3 魚雷自噪聲隨深度變化情況Fig.3 Torpedo self-noise changing with depth

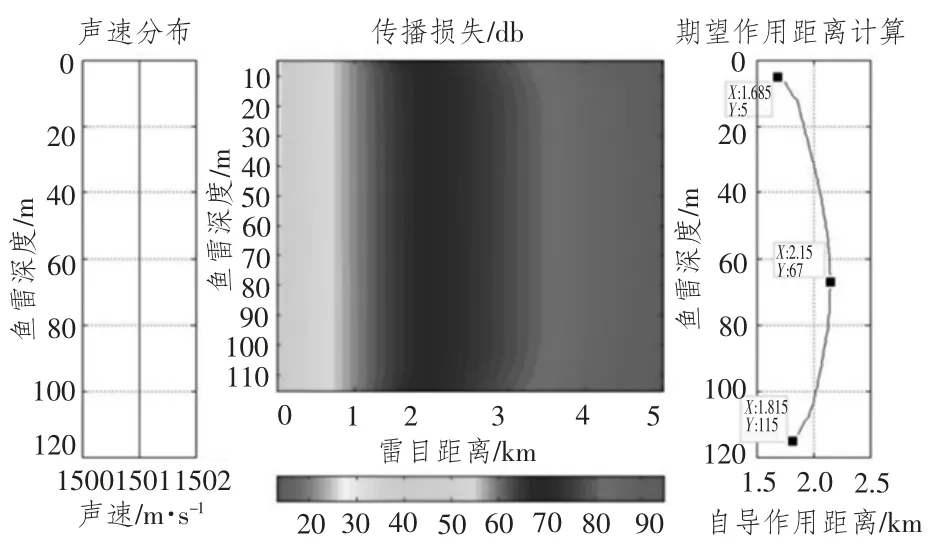
圖4 等聲速條件下的被動自導作用距離Fig.4 Passive homing system detection range in invariable SSP

圖5為負梯度條件下的被動自導作用距離仿真。可以看出，負梯度條件下，70 m 深度上自導作用距離最大，約2.1 km。而在靠近海面和海底深度上，自導作用距離僅1.65 km和1.77 km 左右。這是由于負梯度條件下，聲線往海底方向彎曲，使得大于聲源深度上傳播損失較小，而魚雷自噪聲在67 m 深度上最低，魚雷自噪聲和傳播損失在深度上的分布共同決定了魚雷被動自導最佳搜索深度略大于自噪聲最低深度。

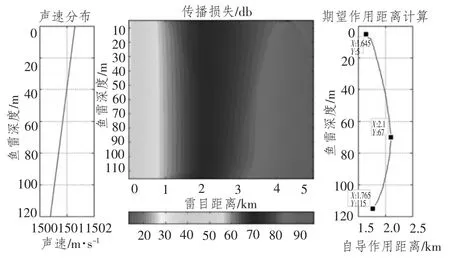
圖5 負梯度條件下的被動自導作用距離Fig.5 Passive homing system detection range in reverse gradient SSP

圖6為正梯度條件下的被動自導作用距離仿真。可以看出，正梯度條件下，靠近海面的深度上自導作用距離較大，最大值2.29 km 出現在10 m深度。而在靠近海底深度上，超過自導作用距離僅1.67 km。這是由于聲速梯度達0.175 s－1，正梯度條件下，聲線往海面方向彎曲，在接近海面深度形成表面聲道。傳播損失成為影響被動自導搜索深度的主要因素。同時可以看出，29 m 深度上作用距離僅1.855 km，這是由于該深度上形成聲影區，進行魚雷深度設定時應避開此深度。

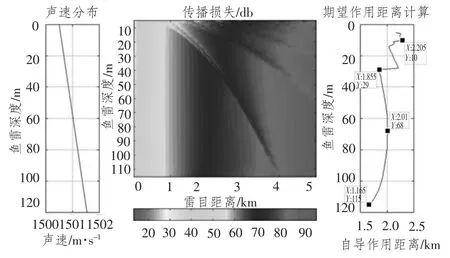
圖6 正梯度條件下的被動自導作用距離Fig.6 Passive homing system detection range in positive gradient SSP

圖7為負躍層條件下的被動自導作用距離仿真，躍層深度在9～20 m，聲速梯度為－1.636 s－1。可以看出，負躍層條件下，被動自導作用距離在最靠近海面5 m 深度上最大，約2.2 km;在19 m 左右的躍層深度上，作用距離僅1.825 km;在靠近海底深度上左右距離最小，僅1.57 km。在躍層以上，由于魚雷與目標處于聲躍層的同側，傳播損失遠小于躍層以下，因此作用距離最大。躍層以下深度上，由于躍層的影響，自導作用距離總體上小于躍層以上。但由于躍層以下為正聲速梯度，聲線向海面彎曲，使得靠近海底深度上自導作用距離最小。同時，由于躍層以下正聲速梯度和67 m 深度上自噪聲最低，使得躍層以下自導作用距離最大值1.94 km 出現在69 m 深度。

3 結 語

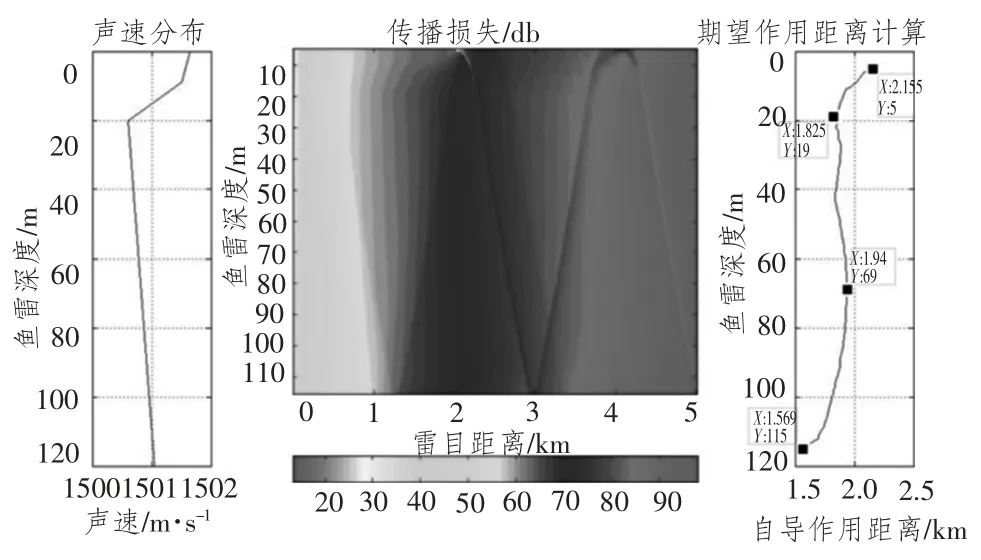
圖7 負躍層條件下的被動自導作用距離Fig.7 Passive homing system detection range in negative thermocline SSP

仿真分析結果表明，在4 種典型聲速分布條件下，由于魚雷自噪聲和傳播損失在水平深度上的差異，不同深度上的被動自導作用距離相差30%～40%。因此，魚雷被動聲自導反艦搜索時，搜索深度設定嚴重影響魚雷被動自導搜索效果，進而影響魚雷作戰效能的發揮。在進行魚雷搜索深度參數設定時，除了魚雷航行深度限制、作戰訓練任務要求等約束，應綜合考慮海面和海底散射為主要因素影響下的魚雷自噪聲，海區聲速梯度條件影響下的傳播損失在深度上的分布。

大量仿真分析表明，在等聲速條件下，魚雷被動聲自導反艦最佳搜索深度通常為自噪聲最低深度;負梯度條件下，魚雷設定深度應略大于自噪聲最低深度;正梯度條件下，滿足魚雷最小極限深度條件的前提下，魚雷設定深度應選擇靠近海面的深度，同時注意避開魚雷被動聲自導盲區;在負躍層條件下，魚雷設定深度應在躍層上方，若戰術或其他條件限制下魚雷不事宜在躍層以上搜索時，應選擇躍層以下自噪聲最低深度附近。

［1］PAUL C E，蔡志明，譯.水聲建模與仿真［M］.北京:電子工業出版社，2005:225－239.

［2］徐園園，王明洲，蔣繼軍.基于聲散射的魚雷自噪聲場空間特性［J］.艦船科學技術，2013，35(9):130－133.

［3］徐園園，王明洲，蔣繼軍.基于雙基地模型的魚雷自噪聲仿真預報［J］.艦船科學技術，2012，34(12):24－29.

［4］徐園園，王明洲，蔣繼軍.基于聲散射模型的魚雷自噪聲特性分析及仿真預報［J］.魚雷技術，2013，21(2):105－109.

［5］笪良龍.海洋水聲環境效應建模與應用［M］.北京:科學出版社，2012:143－151.

［6］MICHAEL A A.Principles of sonar performance modeling［M］.Berlin:Springer ＆ Chichester:Praxis，2010:53－122.