密度泛函活性理論中的Rényi 熵, Tsallis 熵和Onicescu 信息能
劉述斌 榮春英 吳澤民 盧 天(湖南師范大學(xué)化學(xué)化工學(xué)院, 資源精細化與先進材料湖南省高校重點實驗室, 化學(xué)生物學(xué)及中藥分析教育部重點實驗室,長沙 4008; Research Computing Center, University of North Carolina, Chapel Hill, North Carolina 7599-40, USA;北京科音自然科學(xué)研究中心, 北京 000)
密度泛函活性理論中的Rényi 熵, Tsallis 熵和Onicescu 信息能
劉述斌1,2,*榮春英1,*吳澤民1盧 天3
(1湖南師范大學(xué)化學(xué)化工學(xué)院, 資源精細化與先進材料湖南省高校重點實驗室, 化學(xué)生物學(xué)及中藥分析教育部重點實驗室,長沙 410081;2Research Computing Center, University of North Carolina, Chapel Hill, North Carolina 27599-3420, USA;3北京科音自然科學(xué)研究中心, 北京 100022)
根據(jù)密度泛函理論, 分子的電子密度確定了該體系基態(tài)下的所有性質(zhì), 其中包括結(jié)構(gòu)和反應(yīng)活性. 如何運用電子密度泛函有效地預(yù)測分子反應(yīng)活性仍然是一個有待解決的難題. 密度泛函活性理論(DFRT)傾力打造這樣一個理論和概念架構(gòu), 使得運用電子密度以及相關(guān)變量準(zhǔn)確地預(yù)測分子的反應(yīng)特性成為可能. 信息理論方法的香農(nóng)熵和費舍爾信息就是這樣的密度泛函, 研究表明, 它們均可作為反應(yīng)活性的有效描述符. 本文將在DFRT框架中介紹和引進三個密切相關(guān)的描述符, Rényi熵、Tsallis熵和Onicescu信息能. 我們準(zhǔn)確地計算了它們在一些中性原子和分子中的數(shù)值并討論了它們隨電子數(shù)量和電子總能量的變化規(guī)律. 此外, 以第二階Onicescu信息能為例, 在分子和分子中的原子兩個層面上, 系統(tǒng)地考察了其隨乙烷二面角旋轉(zhuǎn)的變化模式. 這些新慨念的引入將為我們深入洞察和預(yù)測分子的結(jié)構(gòu)和反應(yīng)活性提供額外的描述工具.
Rényi熵; Tsallis熵; Onicescu信息能; 香農(nóng)熵; 密度泛函活性理論
1 Introduction
According to density functional theory,1any property of a molecule in the ground state is determined by its electron density. These properties could be structure, reactivity, and many others. While in the past few decades, focuses have been paid to search for better behaved density functionals to approximate energy components such as kinetic and exchange-correlation energies, there is an integral piece of information that is still missing. That is, we still do not know much about how to employ density functionals to predict molecular reactivity. The endeavor to employ quantities directly related to the electron density and its associated quantities as descriptors to establish a conceptual framework so that quantitative predictions of chemical reactivity are possible is called density functional reactivity theory (DFRT).1–4Since quantities from information theory involve probability functions such as the electron density, they are natural choices as reactivity descriptors in DFRT. These quantities include Shannon entropy,5Fisher information,6Ghosh-Berkowitz-Parr entropy,7and information gain.8–10The effort to make use of these quantities in molecular reactivity study in DFRT is called the information-theoretic approach. Very recently, we have intensively investigated the properties of these quantities for atoms and molecules and applied them to quantify reactivity for a number of systems.11–18
In this contribution, we expand the scope of the DFRT study by exploring three closely related quantities in the informationtheoretic approach. They are Rényi entropy,19Tsallis entropy,20and Onicescu information energy.21The purpose of the present work is to formally introduce these quantities into DFRT and set the stage for their further applications in reactivity predictions in the future.
2 Theoretical framework
Given an electron density distribution ρ(r) and density gradientin the ground state of an N-electron system, which satisfies the normalization condition, ∫ρ(r)dr = N, according to the information-theoretic approach, Shannon entropy and Fisher information are, respectively, defined,5,6

The Ghosh-Berkowitz-Parr entropy and information gain can be defined accordingly, as detailed elsewhere.7–10These quantities were the recent focus of our extensive studies.11–18Three other quantities, Rényi entropy, Tsallis entropy, and Onicescu information energy, are closely related, whose definitions are as follows.
For a continuous probability distribution like ρ(r), the Rényi entropy of order n, where n ≥ 0 and n ≠ 1, is defined as19
when n approaches to 1, the Rényi entropy, Eq.(3), reduces to the Shannon entropy, Eq.(1). The Tsallis entropy of order n is defined as follows,20
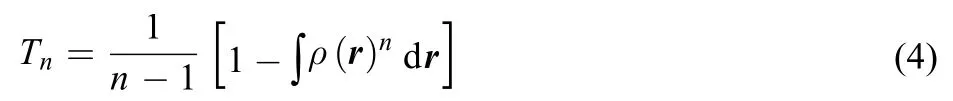
It is a generalization of the standard Boltzmann-Gibbs entropy. The common term in Eqs.(3) and (4) is the integral of the n-th power of the electron density, which can indeed be regarded as a separate definition in its own right. It is called the Onicescu information energy of order n:21
Onicescu introduced this quantity in an attempt to define a finer measure of dispersion distribution than that of Shannon entropy.
These three quantities can similarly be re-defined with the shape function σ(r), which is related to the electron density via ρ(r) ≡ Nσ(r). Eqs.(3–5) become16
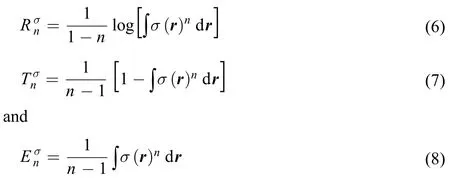
Using the explicit relationship between ρ(r) and σ(r), we can readily prove that
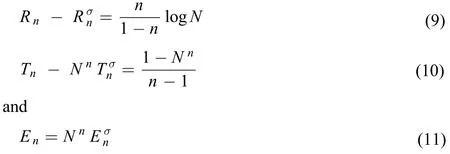
Again, N is the total number of electrons in the system, and n is the order of the quantities studied. In the special case of n = 1, Rényi entropy and Tsallis entropy are both reduced to theShannon entropy, and Onicescu information energy is illdefined because 1/(n–1) diverges. In this work, we consider the cases of n ≥ 2.
Same as the Shannon entropy and Fisher information, these quantities can also be decomposed into atomic contributions through three distinct atom partition schemes, Bader's zeroflux,22Becke's fuzzy atom,23and Hirshfeld's stockholder24approaches. As have been shown recently, these three approaches yield similar results.16In this work, we investigate atoms-in-molecules behavior using Hirshfeld's stockholder partition scheme. For any quantity above Q[ρ], the evaluation of the total molecular value can be rewritten as the sum of atomic contributions,
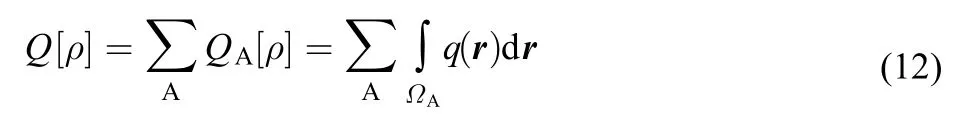
where QA[ρ] is the atomic contribution from atom A and ΩAas the atomic basin of atom A in the molecule.
3 Computational details
In this work, we consider the cases n = 2 and n = 3 in Eqs. (3–11). That is, we only examine the behavior of Rényi entropy, Tsallis entropy, and Onicescu information energy of orders 2 and 3. Higher orders of these quantities can be investigated similarly. All of these formulas have been successfully implemented in the Multiwfn 3.3 package developed by one of the present authors,25whose reliability and applicability have extensively been tested before. As illustrative examples, we present below results of these new information-theoretic quantities for a number of atomic and molecular systems.
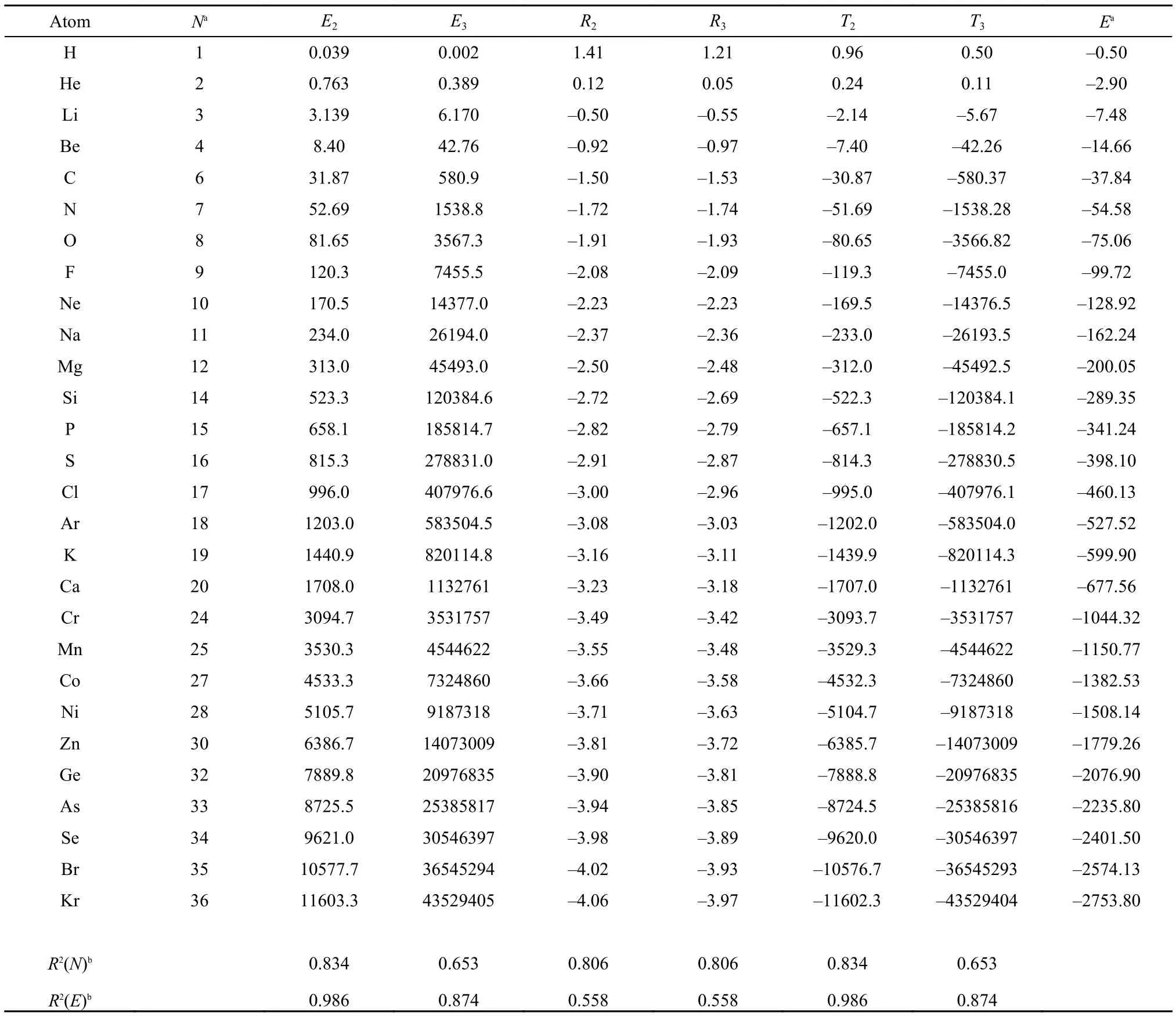
Table1 Atomic values of new information-theoretic quantities (units are in atomic unit) obtained with the total electron density
All electronic wave functions were obtained from the Gaussian 09 package, version D01.26For all atoms and molecules invest-igated in this work, the M062X density functional was employed.27For the choice of basis sets, in atomic calculations, where neutral species from H to Kr were considered, the standard Pople's 6-311G(3df, 3pd) basis set28was used. In molecular calculations, we made use of the augmented version of correlation consistent basis set with added diffuse functions, aug-ccpVDZ,29for all the systems examined. A total of 21 molecular systems were investigated in this work with the general formula of R1R2R3CF with R1, R2, and R3representing alkyl groups such as -H, -CH3, -C2H5, -C3H7, and -C4H9, which were previously considered elsewhere. We denote these molecular species in terms of three substituting groups in the format of (R1R2R3). The molecular values of the Shannon entropy, Fisher information, as well as quantities in Eqs.(3–11) for the orders of 2 and 3 were calculated for these systems. We also calculated the profile of these quantities as a function of the ∠HCCH dihedral angle rotation for the ethane molecule. The ∠HCCH dihedral angle is changed from 0° (staggered conformer) to 360° with the step size of 5°.30The purpose of this profiling study is to examine the change patterns of these quantities with respect to the change of this dihedral angle at both molecular and atoms-in-molecules levels. All molecules were fully optimized. The tight self-consistent field convergence criterion and ultrafine integration grids were employed. Checkpoint files obtained from these Gaussian calculations were used as the input file to obtain these and other information-theoretic quantities.
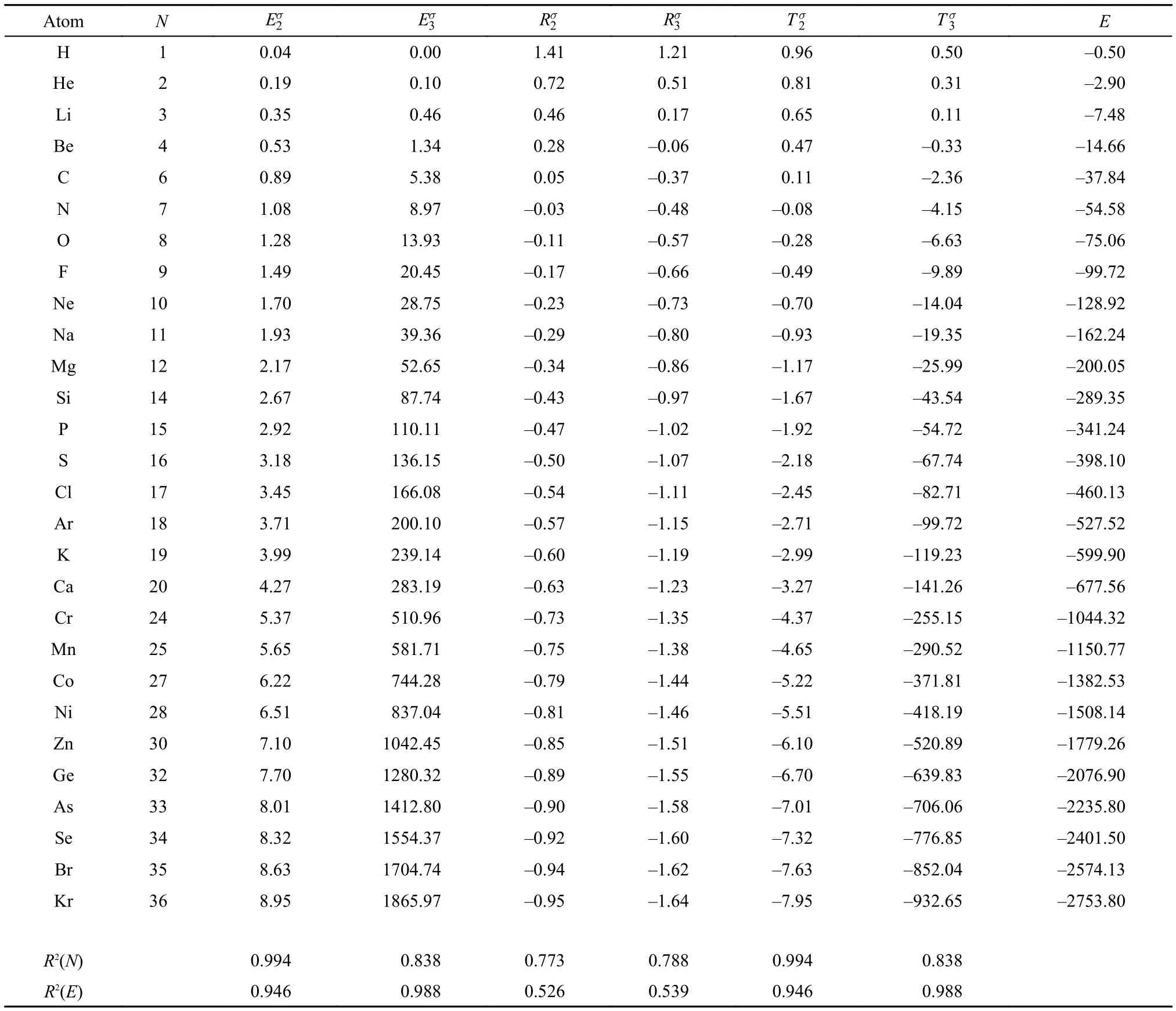
Table2 Atomic values of new information-theoretic quantities (units are in atomic unit) obtained with the shape density for neutral atoms up to Kr
4 Results and discussion
Shown in Table 1 are atomic values of the new informationtheoretic quantities obtained for the total electron density, including Onicescu information energy of orders 2 and 3, E2and E3, Rényi entropy of orders 2 and 3, R2and R3, and Tsallis entropy of orders 2 and 3, T2and T3, respectively, for neutral atoms up to krypton. Also shown in the Table are the total number of electrons N, the total electronic energy E at the M062X/ 6-311G(3df, 3pd) level of theory, and correlation coefficients of these new quantities with respect to both N and E. As can beseen from the Table, E2and E3are always positive and monotonically increasing, but R2, R3, T2, and T3are not always positive or negative, even though they appear to be monotonically decreasing with respect to the total number of electrons. From the values of correlation coefficients R2, we can see that E2and T2have the largest R2value with respect to the total electronic energy. For others, the correlations are also reasonably strong. This particularly strong linear correlation between E2and E could partially explain why E2has been called information energy. Another explanation is to make use of the following identity31-33

for any local strongly decaying quantity q(r). With q(r) ≡ ρ2(r) and after some manipulations, we have
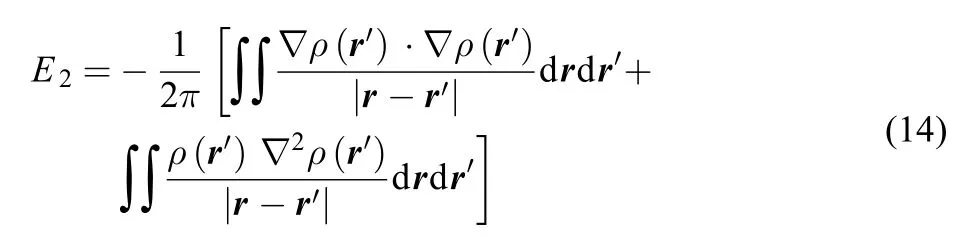
As can be seen from Eq.(14), the double integral form of E2resembles the classical Columbic repulsion between electrons,
except that Eq.(14) involves interactions among ρ(r), ?ρ(r), and ?2ρ(r).
Table 2 exhibits the numerical results of these informationtheoretic quantities obtained for the shape density, Eqs.(6–8), of orders 2 and 3, respectively, for neutral atoms from H to Kr. Their correlation coefficients with both E and N are also appended in the Table. It becomes clear that the shape function version of these new information-theoretic quantities possesses different correlations with E and N. Strong linear correlations betweenand N, and betweenand N are seen, so are correlations ofand with respect to the total electronic energy E. These linear relationships can be harnessed to predict properties for atoms and ions.
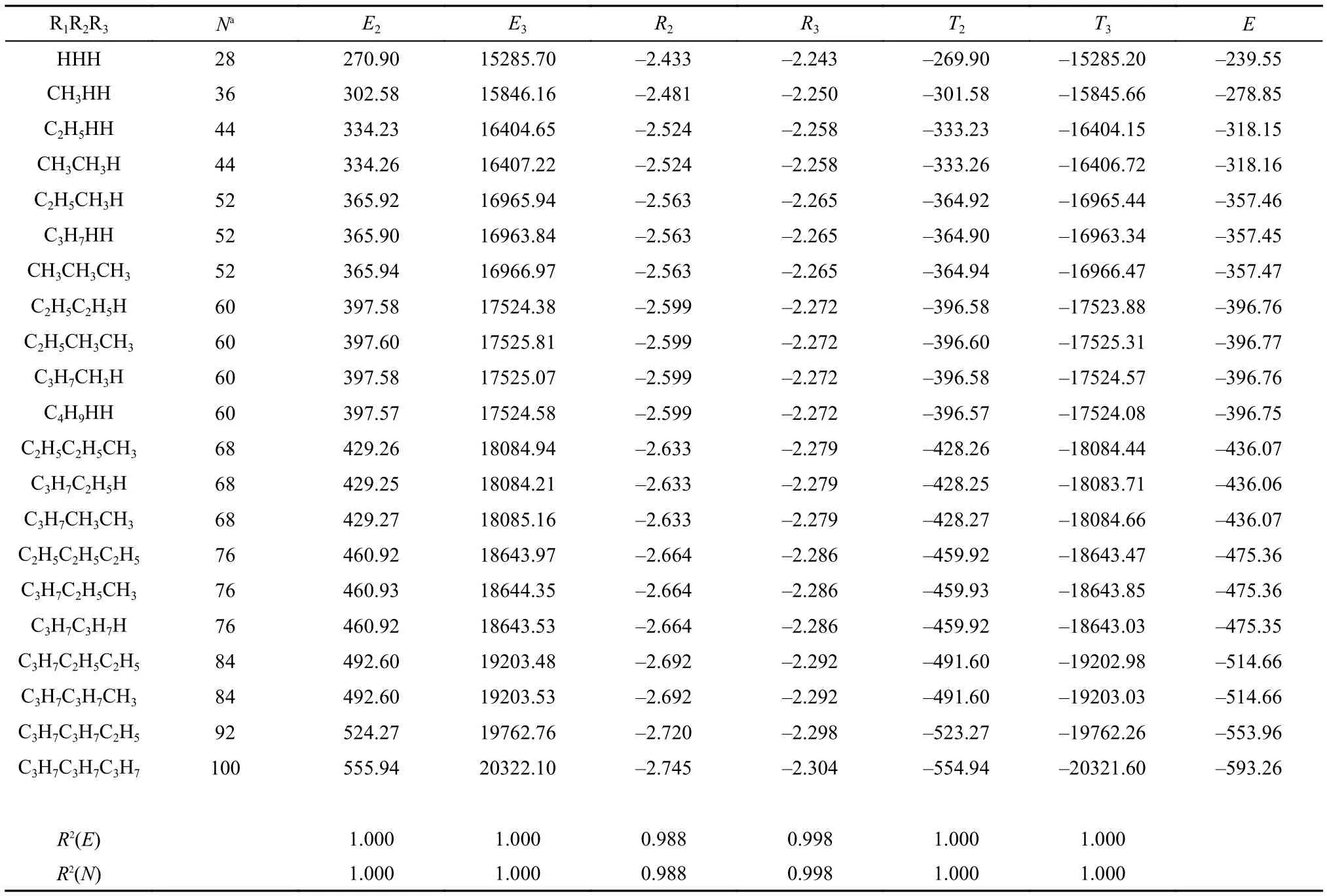
Table3 Molecular values of new information-theoretic quantities (units are in atomic unit) obtained with the total electron density
For molecules, Table 3 illustrates numerical results for 21 species of the same category with the general molecular formula of R1R2R3C-F. To save space, we do not show their counterparts in terms of the shape function. Their correlation coefficients with N and E are also shown, which, as can be seen from the Table, are remarkable. Since the electron density determines everything in the ground state, it is not surprising that strong correlations among different quantities in different sys-tems can be obtained in some cases. These amazingly strong correlations likely originate from the fact that this set of molecules is similar in nature. Whether or not these linear relationships persist in other systems remains to be validated, but based on the results from our previous studies, the answer to above question is likely no.15
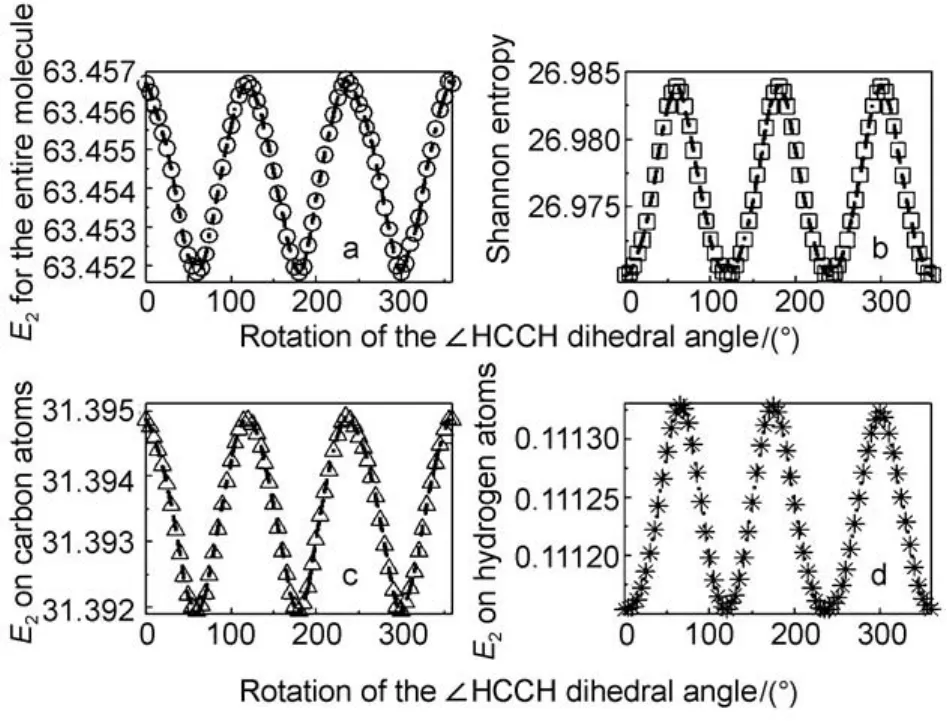
Fig.1 Profiles of information-theoretic quantities as a function of the∠ HCCH dihedral angle for the ethane molecule
To demonstrate different behaviors of these quantities at the level of atoms in molecules, as an illustrative example, shown in Fig.1 are the profiles of the second-order Onicescu information energy E2as a function of the ∠HCCH dihedral angle for the ethane molecule at both molecular and atoms-in-molecules levels. Fig.1a is the second-order Onicescu information energy at the molecular level, Fig.1b is the molecular value of the Shannon entropy, Fig.1c denotes the atomic E2value for the carbon atom in C2H6, and Fig.1d represents the atomic E2value for the hydrogen atom in C2H6. While in all the cases smoothly varying curves are observed as the dihedral angle increases from 0° (the staggered conformer) to 360°, we can clearly see that the changing patterns are markedly different. The secondorder Onicescu information energy is the largest (Fig.1a) at∠HCCH = 0°, that is, when the conformer is staggered, so is the atomic value of E2on the carbon atom (Fig.1c). However, for its value on the hydrogen atom, it becomes the least, as shown in Fig.1d. This latter behavior is also true for the molecular value of the Shannon entropy exhibited in Fig.1b.11Overall, the profiling changing pattern of the molecular value of the second-order Onicescu information energy as well as its atomic value on the carbon atom in ethane is like a cosine curve, whereas for its atomic value on the hydrogen atom together with the molecular value of the Shannon entropy, the changing pattern resembles a sine curve. These different patterns on molecular and atomic levels were unveiled elsewhere for other information-theoretic quantities.11,16These different behaviors will likely result in different reactivity properties for different atoms in molecules.
5 Concluding remarks
As a continuation of our recent efforts to develop an information-theoretic approach in density functional reactivity theory, in this work, we have introduced three new quantities, Rényi entropy, Tsallis entropy, and Onicescu information energy, into the framework of DFRT. These quantities are all functionals of the electron density and they are closely related to each other as well. These quantities can be represented not only for the electron density, but also for the shape function, as have been shown in this work. We evaluated the second and third orders of these quantities for a number of neutral atomic and molecular systems under both the electron density and shape function representations. Their correlations with the total number of electrons and electronic energy have also been obtained and discussed. In addition, using the second-order Onicescu information energy as an example, we examined the changing pattern of this quantity as a function of the ∠HCCH dihedral angle for the ethane molecule at both molecular and atoms-in-molecules levels, where different changing patterns have been observed. It is our belief that these new quantities can be used to serve as novel reactivity descriptors in DFRT to provide more in-depth insights for the accurate predictions of structure and reactivity properties for molecular systems. More studies along this line are in progress and will be reported elsewhere.
(1)Parr, R. G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Clarendon Press: Oxford, England, 1989.
(2)Geerlings, P.; DeProft, F.; Langenaeker, W. Chem. Rev. 2003, 103, 1793. doi: 10.1021/cr990029p
(3)Chattaraj, P. K.; Sarkar, U.; Roy, D. R. Chem. Rev. 2006, 106, 2065. doi: 10.1021/cr040109f
(4)Liu, S. B. Acta Phys. -Chim. Sin. 2009, 25, 590. [劉述斌. 物理化學(xué)學(xué)報, 2009, 25, 590.] doi: 10.3866/PKU.WHXB20090332
(5)Shannon, C. E. Bell Syst. Tech. J. 1948, 27, 379. doi: 10.1002/bltj.1948.27.issue-3
(6)Fisher, R. A. Proc. Cambridge Philos. Soc.1925, 22, 700. doi: 10.1017/S0305004100009580
(7)Ghosh, S. K.; Berkowitz, M.; Parr, R. G. Proc. Natl. Acad. Sci. U. S. A. 1984, 81, 8028. doi: 10.1073/pnas.81.24.8028
(8)Kullback, S.; Leibler, R. A. Ann. Math. Stat. 1951, 22, 79. doi: 10.1214/aoms/1177729694
(9)Nalewajski, R. F.; Parr, R. G. Proc. Natl. Acad. Sci. U. S. A. 2000, 97, 8879. doi: 10.1073/pnas.97.16.8879
(10)Nalewajski, R. F.; Parr, R. G. J. Phys. Chem. A 2001, 105, 7391. doi: 10.1021/jp004414q
(11)Rong, C. Y.; Lu, T.; Liu, S. B. J. Chem. Phys. 2014, 140, 024109. doi: 10.1063/1.4860969
(12)Liu, S. B.; Rong, C. Y.; Lu, T. J. Phys. Chem. A 2014, 118, 3698. doi: 10.1021/jp5032702
(13)Rong, C. Y.; Lu, T.; Chattaraj, P. K.; Liu, S. B. Indian J. Chem., Sect. A 2014, 53, 970.
(14)Liu, S. B. J. Chem. Phys. 2014, 141, 194109. doi: 10.1063/1.4901898
(15)Zhou, X. Y.; Rong, C. Y.; Lu, T.; Liu, S. B. Acta Phys. -Chim. Sin. 2014, 30, 2055. [周夏禹, 榮春英, 盧 天, 劉述斌. 物理化學(xué)學(xué)報, 2014, 30, 2055.] doi: 10.3866/PKU.WHXB201409193
(16)Rong, C. Y.; Lu, T.; Ayers, P. W.; Chattaraj, P. K.; Liu, S. B. Phys. Chem. Chem. Phys. 2015, 17, 4977; Phys. Chem. Chem. Phys. 2015, 17, 11110.
(17)Liu, S. B. J. Phys. Chem. A 2015, 119, 3107. doi: 10.1021/acs.jpca.5b00443
(18)Wu, W. J.; Wu, Z. M., Rong, C. Y.; Lu, T.; Huang, Y.; Liu, S. B. J. Phys. Chem. A 2015, 119, 8216.
(19)Rényi, A. Probability Theory; North-Holland: Amsterdam, 1970.
(20)Tsallis, C. J. Stat. Phys. 1988, 52, 479. doi: 10.1007/BF01016429
(21)Onicescu, O. C. R. Acad. Sci. Paris A 1966, 263, 25.
(22)Bader, R. F. W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, England, 1990.
(23)Becke, A. D. J. Chem. Phys. 1988, 88, 2547. doi: 10.1063/1.454033
(24)Hirshfeld, F. Theor. Chim. Acc. 1977, 44, 129. doi: 10.1007/BF00549096
(25)Lu, T.; Chen, F. J. Comput. Chem. 2012, 33, 580. doi: 10.1002/jcc.v33.5
(26)Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; et al. Gaussian 09, Revision D.01; Gaussian Inc.:Wallingford, CT, 2009.
(27)Zhao, Y.; Truhlar, D. G. Theor. Chem. Acc. 2008, 120, 215. doi: 10.1007/s00214-007-0310-x
(28)Ditchfield, R.; Hehre, W. J.; Pople, J. J. Chem. Phys. 1971, 54, 724. doi: 10.1063/1.1674902
(29)Dunning, T. H., Jr. J. Chem. Phys. 1989, 90, 1007.
(30)Liu, S. B. J. Phys. Chem. A 2013, 117, 962. doi: 10.1021/jp312521z
(31)Liu, S. B.; Parr, R. G.; Nagy, A. Phys. Rev. A 1995, 52, 2645. doi: 10.1103/PhysRevA.52.2645
(32)Liu, S. B. Int. J. Quantum Chem. 2006, 106, 1762.
(33)Liu, S. B. J. Chem. Phys. 2007, 126, 191107. doi: 10.1063/1.2741244
Rényi Entropy, Tsallis Entropy and Onicescu Information Energy in Density Functional Reactivity Theory
LIU Shu-Bin1,2,*RONG Chun-Ying1,*WU Ze-Min1LU Tian3
(1Key Laboratory of Sustainable Resources Processing and Advanced Materials of Hunan Province College, Key Laboratory of Chemical Biology and Traditional Chinese Medicine Research (Ministry of Education of China), College of Chemistry and Chemical Engineering, Hunan Normal University, Changsha 410081, P. R. China;2Research Computing Center, University of North Carolina, Chapel Hill, North Carolina 27599-3420, USA;3Beijing Kein Research Center for Natural Sciences, Beijing 100022, P. R. China)
Density functional theory dictates that the electron density determines everything in a molecular system’s ground state, including its structure and reactivity properties. However, little is known about how to use density functionals to predict molecular reactivity. Density functional reactivity theory is an effort to fill this gap: it is a theoretical and conceptual framework through which electron-related functionals can be used to accurately predict structure and reactivity. Such density functionals include quantities from the information-theoretic approach, such as Shannon entropy and Fisher information, which have shown great potential as reactivity descriptors. In this work, we introduce three closely related quantities: Rényi entropy, Tsallis entropy, and Onicescu information energy. We evaluated these quantities for a number of neutral atoms and molecules, revealing their scaling properties with respect to electronic energy and the total number of electrons. In addition, using the example of second-order Onicescu informationenergy, we examined how its patterns change with the angle of dihedral rotation of an ethane molecule at both the molecular level and atoms-in-molecules level. Using these quantities as additional reactivity descriptors, researchers can more accurately predict the structure and reactivity of molecular systems.
Rényi entropy; Tsallis entropy; Onicescu information energy; Shannon entropy, Density functional reactivity theory
O641
10.3866/PKU.WHXB201509183
Received: August 12, 2015; Revised: September 18, 2015; Published on Web: September 18, 2015.
*Corresponding authors. LIU Shu-Bin, Email: shubin@email.unc.edu. RONG Chun-Ying, Email: rongchunying@aliyun.com;
Tel: +86-13739068784.
The project was supported by the National Natural Science Foundation of China (21503076), and Aid Program for Science and Technology Innovative Research Team in Higher Educational Institutions of Hunan Province, China (Xiang Jiao Tong [2012]318).
國家自然科學(xué)基金(21503076)及湖南省高校科技創(chuàng)新團隊支持計劃(湘教通[2012]318號)資助項目
?Editorial office of Acta Physico-Chimica Sinica

