關于切點三角形的幾個有趣性質

●尚品山(榆林第二實驗中學陜西榆林718000)

關于切點三角形的幾個有趣性質

●尚品山(榆林第二實驗中學陜西榆林718000)

常庚哲先生在1980年第2期的《數學通報》中給出了與內心的切點三角形有關的2個優美不等式.筆者受此啟發，對切點三角形的相關性質也進行了一些探索與研究，得到如下結果.

為了敘述簡便，文中約定:△ABC與其切點△A'B'C'的邊長分別為a，b，c與a'，b'，c';△ABC的面積、半周長、內外切圓的半徑及內心到各頂點的距離分別為Δ，s，r，R及R1，R2，R3.

圖1

引理1在△A'B'C'中，有

證明略.

引理2［1］在△ABC中，有如下恒等式:

引理3［2］在△ABC中，有如下不等式:

證明根據柯西不等式知

結合式(2)得

而由式(5)可知

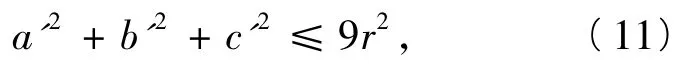
從而由式(10)和式(11)可得

另由海倫公式及半角余弦公式可得

根據均值不等式并結合式(14)，得

從而由式(12)和式(15)即得欲證.

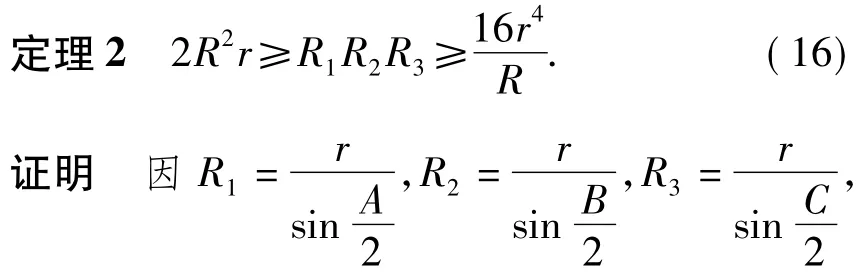
結合式(4)和式(6)，得

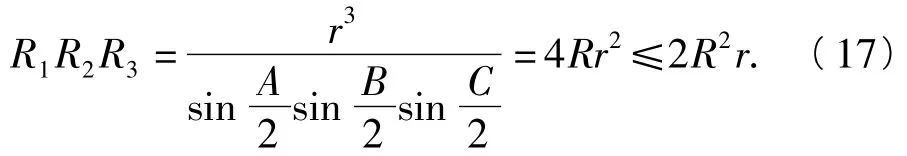
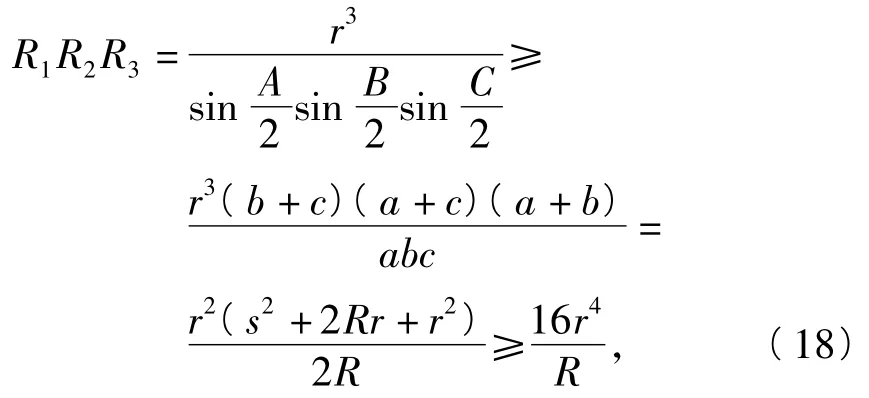
從而由式(17)、式(18)即得欲證.

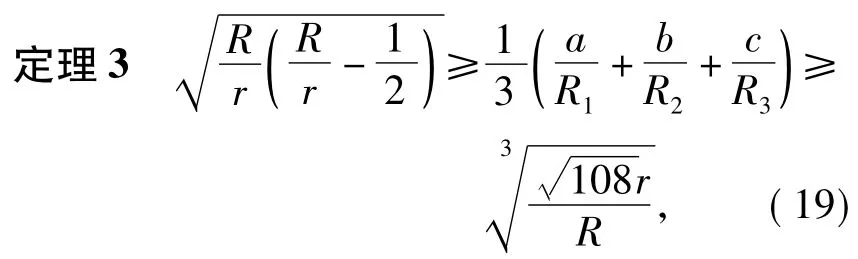
證明根據柯西不等式知

而由定理2的證明過程易知

另由熟知的三角形恒等式

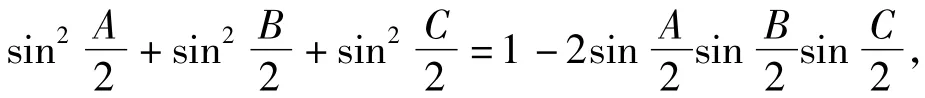
并結合式(4)得

則由式(20)知

從而利用式(5)有

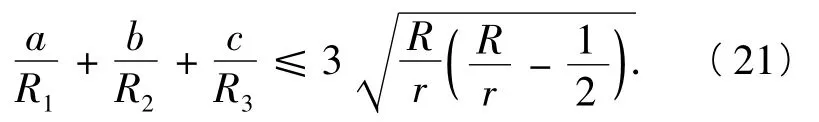
又由均值不等式并結合式(3)、式(7)、式(17)，得

從而由式(21)、式(22)即得欲證.

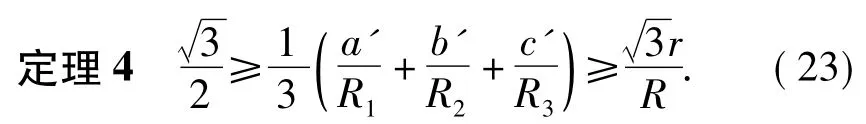
證明由引理1及定理2的證明過程知

從而由式(8)，得

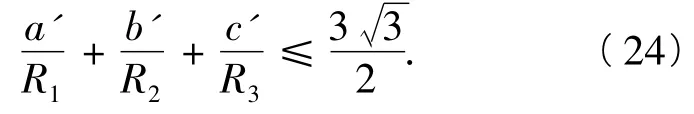
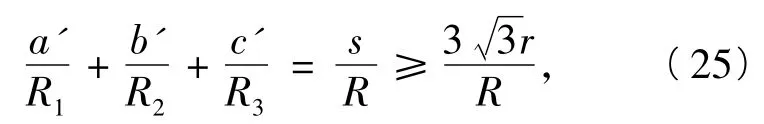
從而由式(24)、式(25)即得欲證.

［1］陳計，葉中豪.初等數學前沿［M］.南京:江蘇教育出版社，1996:90-96.

［2］楊世明.中國初等數學研究文集［M］.鄭州:河南教育出版社，1992:870-886.