基于模糊PID的無人機姿態控制器的設計*

陳 鵬，段鳳陽，張慶杰，鄭志成，肖 偉

(空軍航空大學飛行器控制系，長春 130022)

0 引言

在科技發展的浪潮中，不斷有新的控制理論被提出，而經典的PID控制作為最有效的控制方法還是占據了90%以上的應用領域［1］，常規氣動布局的飛機用PID方法來實現飛行姿態控制的應用亦是非常廣泛［2］。但是經典PID方法沒有考慮飛機在不同大氣環境下模型的不確定性，因而在模型非線性的實際背景下，無法實現精準的控制。相比之下模糊控制方法在模型不確定的情況下仍然可以獲得很好的控制效果，但是它又由于沒有積分項，容易產生穩態誤差［3］。

文中把PID與模糊控制結合，設計一種自適應模糊PID姿態控制器，它同時兼有PID控制較高的控制精度與模糊控制的快速響應性和對不確定模型的適應性。在飛機模型不確定的情況下，仍然可以自適應的調整PID參數，改善被控過程的動態和穩態性能作用，使控制器達到最優。

1 無人機模型與初始PID參數

文中針對的無人機是某型長航時的小型無人機，具有細長機身大展弦比機翼的特點。在研究無人機的穩定性和操縱性時，首先要對飛機模型進行縱向運動和橫航向運動的解耦［4］，然后針對該型無人機工作的平衡點對飛行縱向數學模型進行配平，根據平衡點處的飛行狀態寫出小擾動方程［5］，從而完成飛機模型的線性化處理。文中以高度100 m、速度30 m/s的平飛狀態下對無人機進行配平及線性化處理，得到飛機的狀態方程，根據狀態方程推導出飛機升降舵到俯仰角的傳遞函數G(s)，并據此整定出初始PID參數Kp0，Ki0，Kd0［6］。

2 模糊PID姿態控制器的設計

傳統的PID可以在模型確定的系統中起到不錯的控制效果，但在處理非線性時變模型時，固定的參數使得控制器無法達到最優的效果。文中設計的模糊PID的姿態控制器能夠在系統模型改變時自適應的調整PID控制器的參數，使得性能大幅度優化。模糊PID姿態控制器如圖2所示，輸入為誤差e及誤差的變化率ec，輸出為PID控制器的參數。由于PID控制器有3個參數，所以模糊控制器框圖的內部實際由3個雙輸入單輸出的模糊推理模塊組成。

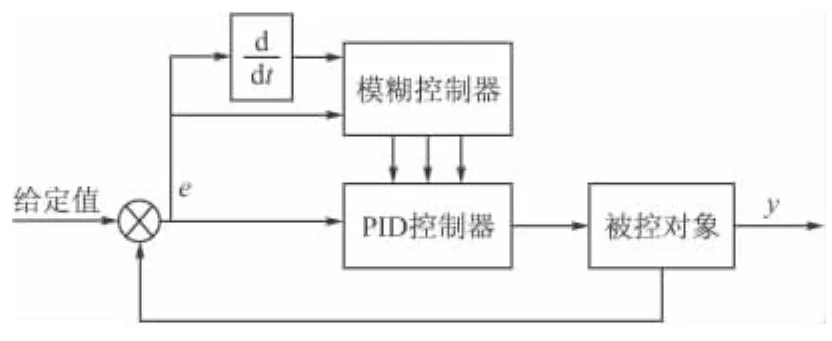
圖1 模糊PID姿態控制器結構圖

2.1 論域的劃分

控制器的兩個輸入變量為誤差e和誤差變化率ec，確定其基本論域為［－5，5］和［－4，4］，選擇量化因子ke和kec分別為1、5/4，把結果映射到模糊論域［－5，5］上。將基本論域劃分為7個模糊子集:{負大，負中，負小，零，正小，正中，正大}(對應的縮寫為NB，NM，NS，ZO，PS，PM，PB)。系統的輸出為 PID 的3 個參數的調整值 ΔKp、ΔKi、ΔKd，確定其基本論域分別為［－10，10］、［－1，1］、［－1，1］，通過比例因子20、2、2，映射到模糊論域［－0.5，0.5］上，輸出端同樣劃分為7個模糊子集:{負大，負中，負小，零，正小，正中，正大}。

2.2 模糊規則的確立

當誤差值e比較大、誤差變化率ec較小時，為了提高系統反應的速度，Kp應取較大值;為了防止超調過大，Ki取較小值;Kd取較小值。當誤差值和誤差變化率中等大小時，Kp、Ki取適中值，Kd應取較大值。當誤差值較小時，Kp應取較大值，為了減少靜態誤差，要增大Ki的取值，而Kd隨著誤差變化率變化而變化。模糊PID就是在初始PID參數的基礎上，運用模糊邏輯對PID參數進行智能調整，如式(1)所示。

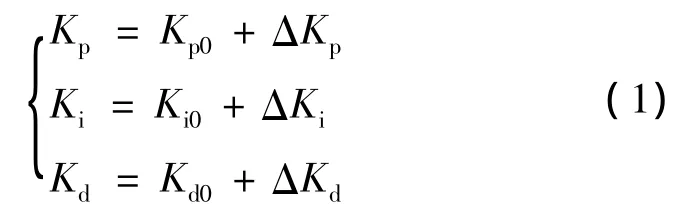
由前述PID調整規則和專家經驗可得到模糊規則表，如表1～表3所示。

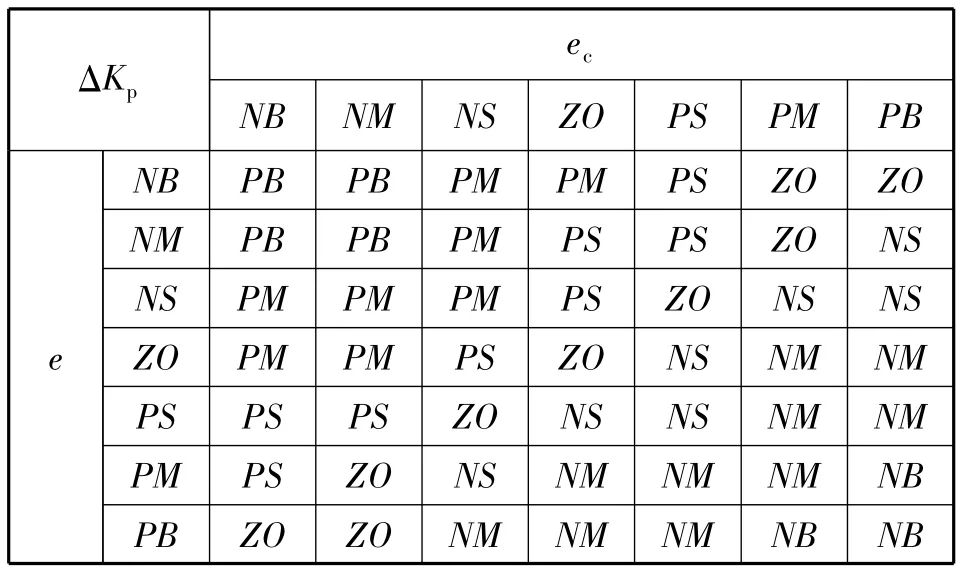
表1 ΔKp模糊規則表

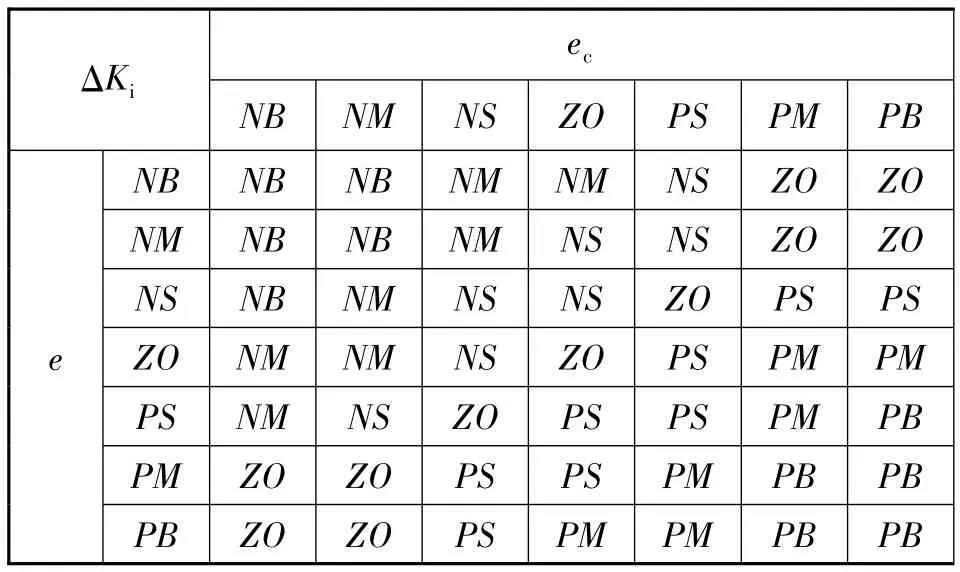
表2 ΔKi的模糊規則表

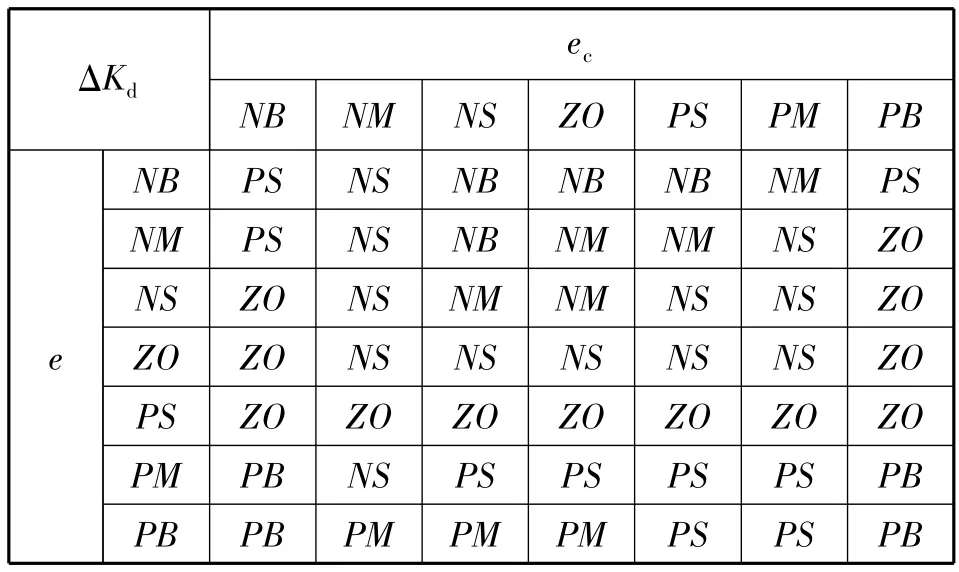
表3 ΔKd的模糊規則表

2.3 隸屬度函數的優化

在設計模糊控制器的過程中，如果模糊規則已經確定，那么模糊控制系統的性能將取決于各個模糊子集的隸屬度函數。模糊控制器的隸屬函數可以設計成三角形、高斯形、梯形等，綜合考慮系統性能，決定采用三角形隸屬函數。通常三角形隸屬度函數的分布是根據模糊子集進行等分，在變量變化不均勻時，如此設計的推理結果不會最優;若是根據專家經驗或者試驗來修正，會有很大的主觀性，同樣不一定是最優結果。文中把遺傳算法應用到隸屬度函數的優化中，這種方法對于傳統搜索方法解決不了的復雜問題和非線性問題具有很好的適應性，通過優勝劣汰的自然法則進行尋優選擇，所得結果收斂于最優值［7］，工作流程如圖2所示。用遺傳算法優化隸屬度函數的主要步驟如下:

1)編碼:把決定隸屬函數形狀的參數轉換成二進制數表示的形式，如式2所示，即轉換為一個個基因段。文中所設計的模糊PID控制器相當于3個普通的模糊控制器分別來控制比例、積分、微分的系數，所以3個控制器的輸出隸屬函數曲線應該是不同的，分別求取最優情況。每種隸屬函數由P1、P2兩個系數來決定，如圖3所示，可轉化為兩個基因段，5種隸屬函數一共有 Pe1、Pe2、Pec1、Pec2、Pp1、Pp2、Pi1、Pi2、Pd1、Pd210個基因段。每個基因由4位的二進制碼來組成，所以每個個體由40位二進制碼組成。

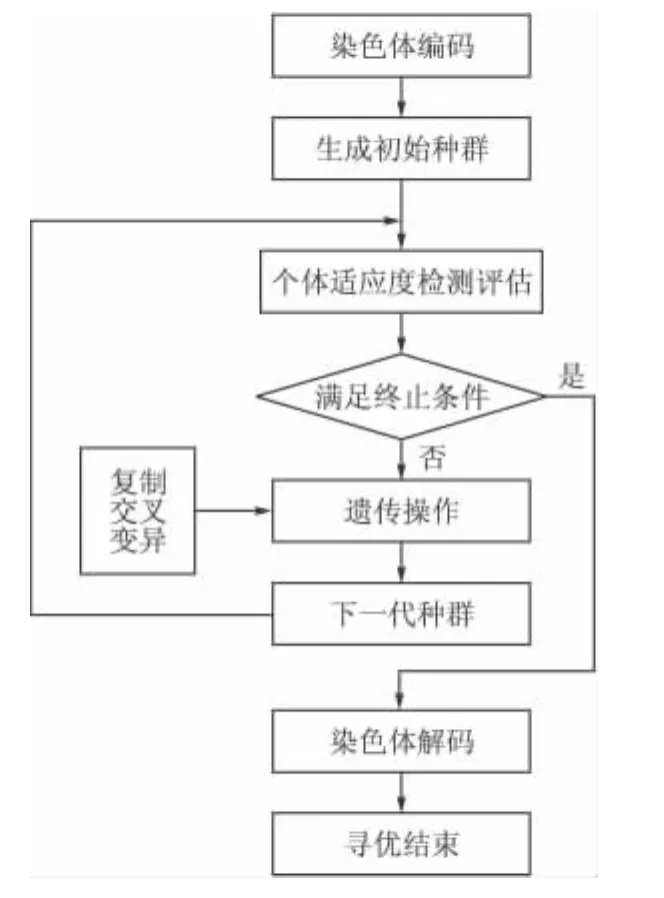
圖2 工作流程圖

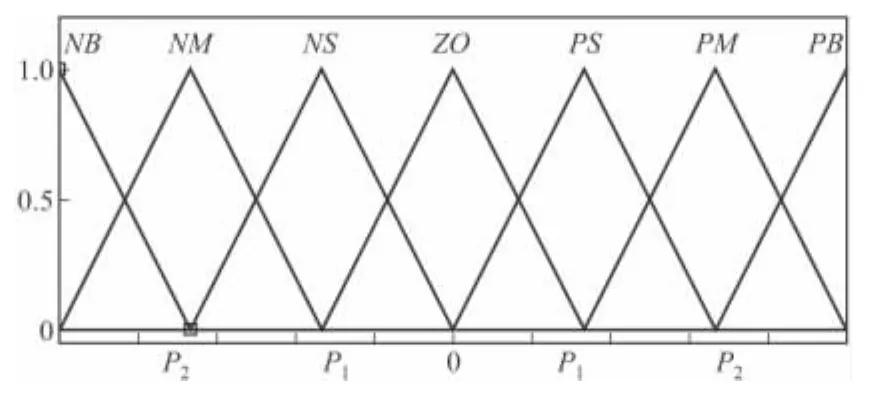
圖3 決定隸屬函數的兩個系數

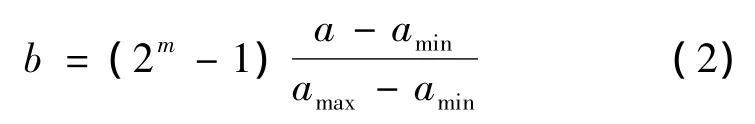
2)適值函數的設計:為綜合考慮目標的準確性和快速性，用誤差絕對值時間積分的結果來設計適值函數。首先設目標函數:

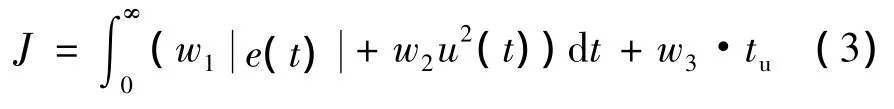
其中:e(t)為系統誤差;u(t)為控制器輸出;tu為上升時間;w為權值。取適值函數f=1/J。即取合適的隸屬函數參數，使得目標函數最小，此時個體適應度最高。

3)選擇:從所有的個體中選出適應性高的個體進行復制和進化，每個個體被復制的概率為:

其中:Psi是第i個個體產生后代的概率;fi為第i個個體的適應度。

4)交叉變異:在新生成的種群中，以Pc的概率進行交叉，在原有的基因型中選出優秀的組合;然后以Pm的概率對個體進行變異操作，產生出新的染色體，它可以改善算法的搜索能力，保證種群的多樣性。

5)最優結果的確定:當隨著優化代數的增加，代價函數值會收斂于一個較小的值，此時遺傳所得的解即是最優的。從中選取適應度最高的染色體，把該染色體解碼，便得到最優化的隸屬函數。

3 系統仿真

文中用到的遺傳基因編碼長度為40，使用的樣本個數為100，交叉概率 Pc為0.9，變異概率 Pm為0.01，終止代數為50。當仿真進行到30代已經開始收斂［8］，目標函數值趨于穩定。最終的結果經過解碼，得到如圖4～圖8所示的隸屬函數。

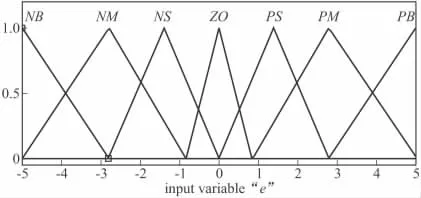
圖4 e隸屬函數

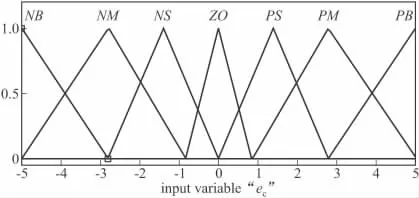
圖5 ec隸屬函數

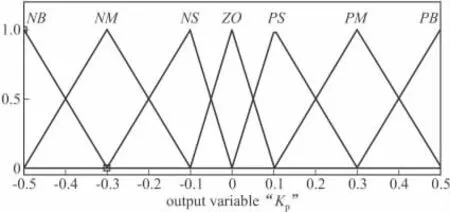
圖6 Kp隸屬函數

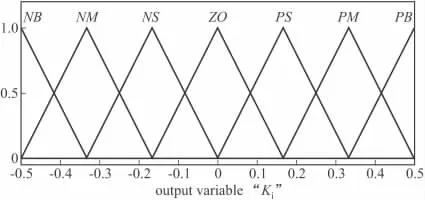
圖7 Ki隸屬函數

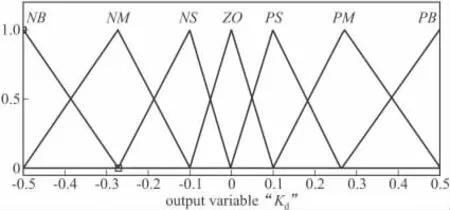
圖8 Kd隸屬函數

把優化后的模糊推理模塊與傳統PID結合，設計完成模糊PID姿態控制器，并對該控制器施加階躍激勵，效果如圖9所示。圖中可以看出，相比傳統PID控制，模糊PID具有很快的反應速度，很高的穩態精度，并且沒有超調。當飛行器收到指令信號之后，可以更迅速、更準確的跟蹤指令信號，完成預定機動。為了測試該姿態控制器在收到連續指令時的響應，對控制系統施加方波激勵，如圖10所示。圖中可以看出，在接受連續方波指令時，模糊PID相比傳統PID的優勢更是明顯，系統具有更好的跟蹤和抗干擾性，可以更快實現穩定的控制，具有出色的動靜態特性。

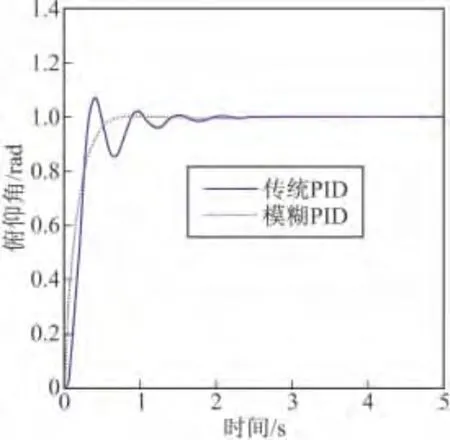
圖9 階躍響應對比

4 總結

文中針對某小型無人機的飛行控制系統設計了模糊PID姿態控制器，通過遺傳算法優化隸屬函數來降低模糊推理過程的人為主觀性。從仿真結果能看出控制系統的動態性能和穩態性能明顯好過傳統的PID控制，文中設計的參數自整定的模糊PID控制器不但有PID控制精度高、易于實現的優點，還有模糊控制器超調小、動態響應快等優點，并且提高了跟蹤和抗干擾性能，可以完成準確快速的姿態控制。

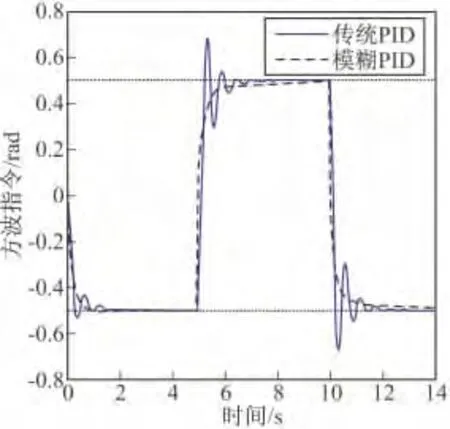
圖10 方波指令的響應對比

［1］Chen G.Conventional and fuzzy PID controllers:An overview［J］.International Journal of Intelligent Control and Systems，1996(1):235-246.

［2］魯道夫.布羅克豪斯.飛行控制［M］.金長江，譯.北京:國防工業出版社，1999.

［3］劉金錕.智能控制［M］.2版.北京:電子工業出版社，2012.

［4］吳森堂，費玉華.飛行控制系統［M］.北京:北京航空航天大學出版社，2005.

［5］文傳源.現代飛行控制系統［M］.北京:北京航空航天大學出版社，2004.

［6］胡壽松.自動控制原理［M］.5版.北京:科學出版社，2007.

［7］E Nakamura.Optimization of fuzzy membership function parameters［C］∥ IEEE International Conference on Systems，Man and Cybernetics，1995 Intelligent Systems for the 21st Century，1995.

［8］薛定宇.控制系統計算機輔助設計——MATLAB語言及應用［M］.2版.北京:清華大學出版社，2006.