有限元模型下大橋合龍頂推方案的研究

孫清娟，趙 杰

(黃河水利職業技術學院，河南開封475004)

一、引 言

預應力混凝土連續剛構橋屬于墩梁固結的超靜定結構，由于溫度變化的作用造成主梁的伸縮變形會使主墩產生偏位，對結構受力產生不利影響。同時在混凝土收縮徐變長期作用下，容易出現跨中下撓、主梁與橋墩水平偏位過大等現象，易導致邊跨支座水平剪切破壞，墩底內力過大［1－3］。為減小這些因素對后期結構承載的不利影響，在合龍階段給梁體施加一定的水平頂推力，以消除合龍溫差、后期收縮徐變因素引起的墩頂水平位移，改善結構受力。目前，潘國兵、殷燦彬、鄒毅松、胡清和等以不同連續剛構橋為工程背景，對合龍頂推力的計算方法進行了研究［4－7］。但由于橋梁結構的差異性，仍需具體問題具體分析。本文在此理論基礎上，引入有限元模型，并以城川河六跨連續剛構橋為工程背景，在給定合龍順序的基礎上，對該橋頂推方案進行一些有益的探討。

二、大橋特點

城川河大橋是霍永高速山西省境內的一座公路橋梁，主橋為(70+4×132+70)m預應力混凝土連續剛構橋(如圖1所示)，設計為左右雙幅，主梁采用單箱單室箱型截面，箱梁根部高8 m，跨中合龍段高3 m，其間梁高按1.6次拋物線變化。單幅橋面寬12 m，底板寬 6 m。主墩墩高 68.8～113.6 m 不等，采用雙肢薄壁墩，單肢采用單箱截面空心薄壁墩，設計荷載為公路I級。

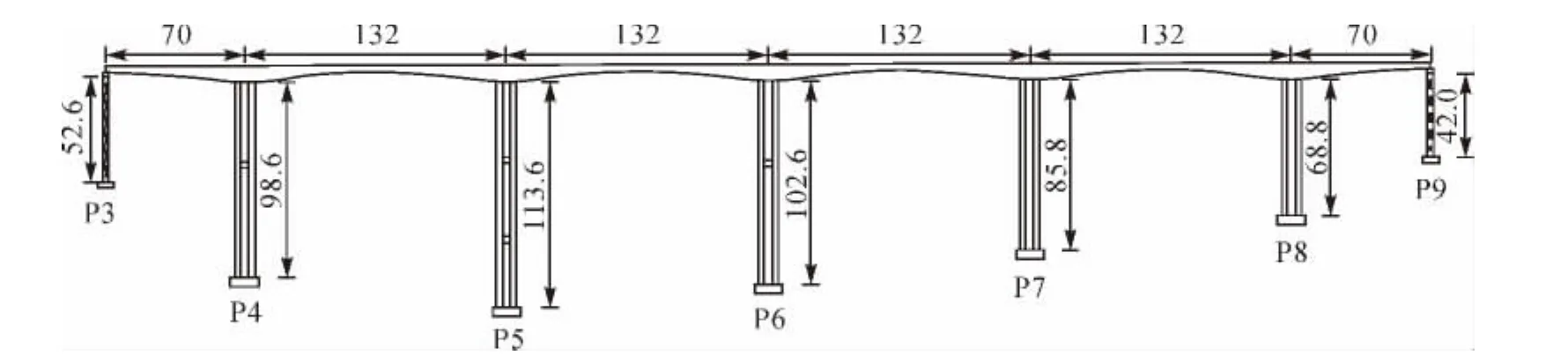
圖1 城川河大橋主橋立面布置圖(單位:m)

三、有限元計算模型

運用Midas/Civil計算軟件，其中采用梁單元，按照施工順序分階段建立橋梁計算模型。全橋共分為36個施工階段，228個梁單元。邊界條件:墩底固結，兩邊跨過渡墩支座模擬成活動鉸。有限元計算模型如圖2所示，圖中數字為相應控制截面節點編號。

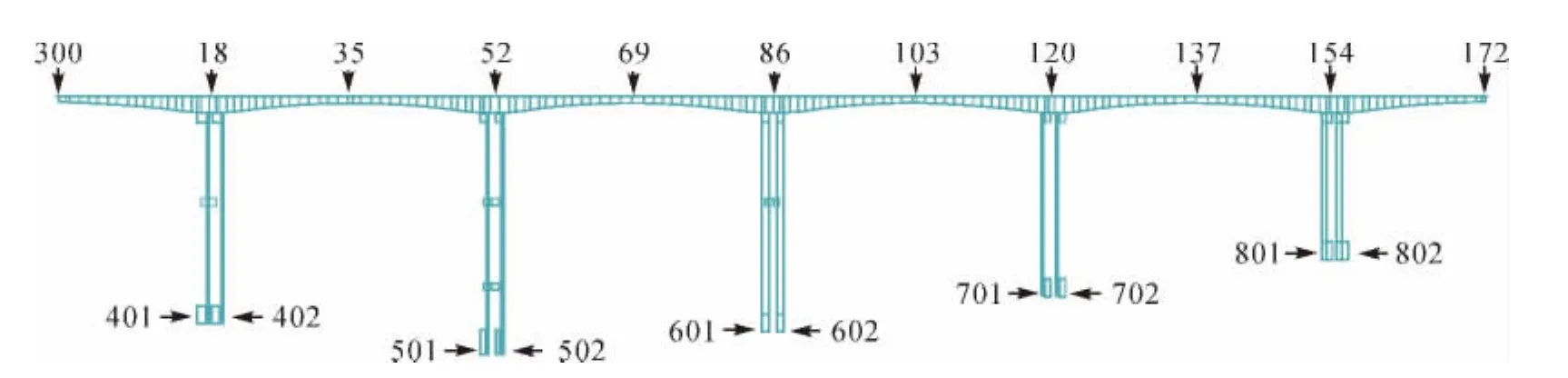
圖2 城川河大橋有限元模型

四、頂推方案

為消除高墩六跨連續剛構橋混凝土收縮徐變與高溫合龍溫差引起的部分墩頂順橋向水平位移，并改善橋墩受力，一般需在跨中合龍段施加相應水平頂推力。

根據該橋的構造特點，結合設計、施工、主梁及橋墩的受力變形特點，在先中跨、然后邊跨、最后次中跨合龍順序基礎上，提出以下3種施加頂推力的方案。

1)方案1:不施加頂推力，如圖3所示。

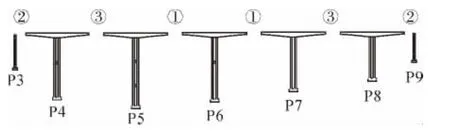
圖3 方案1示意圖

2)方案2:次邊跨、中跨施加頂推力，如圖4所示。

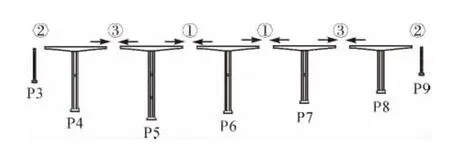
圖4 方案2示意圖

3)方案3:僅次邊跨施加頂推力，如圖5所示。

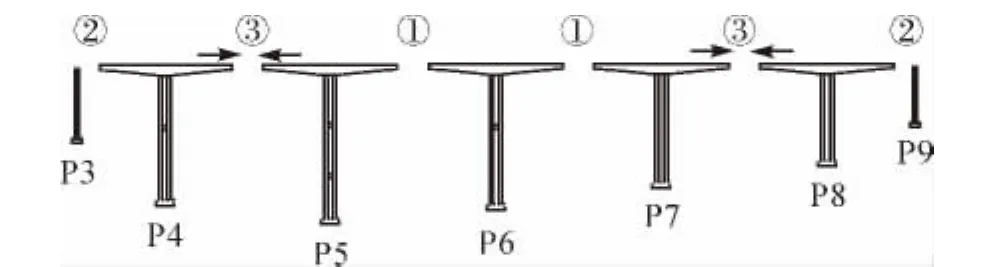
圖5 方案3示意圖

其中，圖3—圖5圈內數字表示合龍順序，相同數字表示同時合龍。

五、頂推力計算

1.頂推量的確定

頂推位移可由以下兩部分組成:合龍溫差變形δ合龍溫差、10年收縮徐變的變形值 δ收縮徐變。考慮成橋后不宜長時間出現過大水平位移，本文取兩者之和的50%。頂推位移δ頂推表達式為

(1)混凝土收縮徐變引起的墩頂位移

為確定在理想合龍條件下(實際合龍溫度與設計相同)，混凝土收縮徐變對墩頂位移產生的影響，按照施工順序進行有限元模擬，計算出不同運營時間各墩頂的順橋向水平位移，如表1、圖6所示。

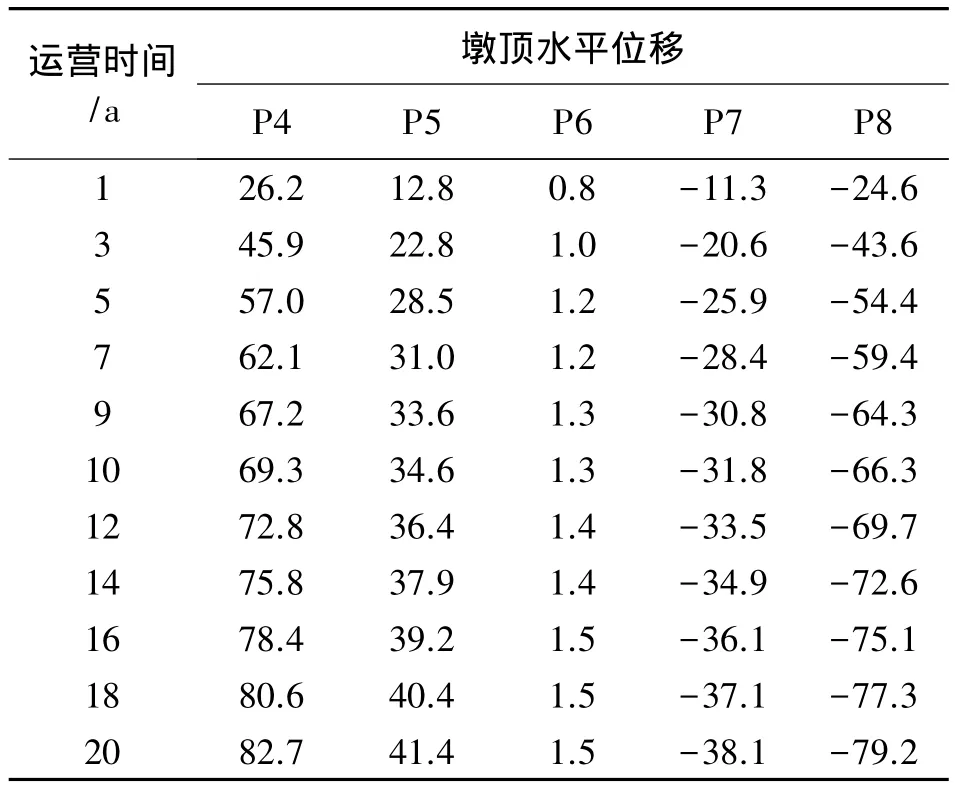
表1 隨運營時間收縮徐變引起的墩頂水平位移 mm

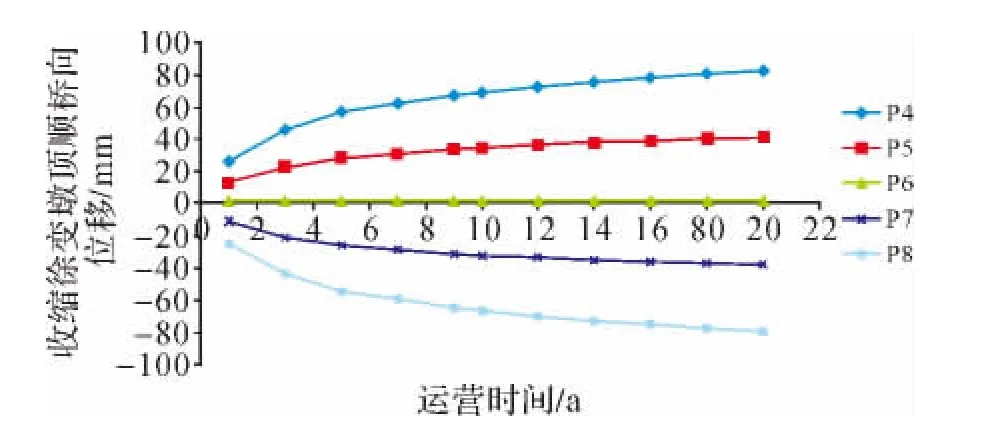
圖6 隨運營時間收縮徐變引起的墩頂水平位移

從表 1、圖6 可以看出墩 P4、P5、P7、P8 收縮徐變引起的位移，隨著運營時間的增加，增速先快速增長后逐漸減緩，趨于穩定。墩P6受影響最小，幾乎不受影響。

(2)合龍溫差引起的墩頂水平位移

大橋實際合龍溫度與設計合龍溫度不同時，由于溫差作用，將使梁體產生相應的伸長或縮短，從而引起墩頂偏位。高溫合龍引起的墩頂水平位移，相當于結構整體由實際合龍溫度下降到設計溫度引起的各墩頂的水平位移，如表2、圖7所示。

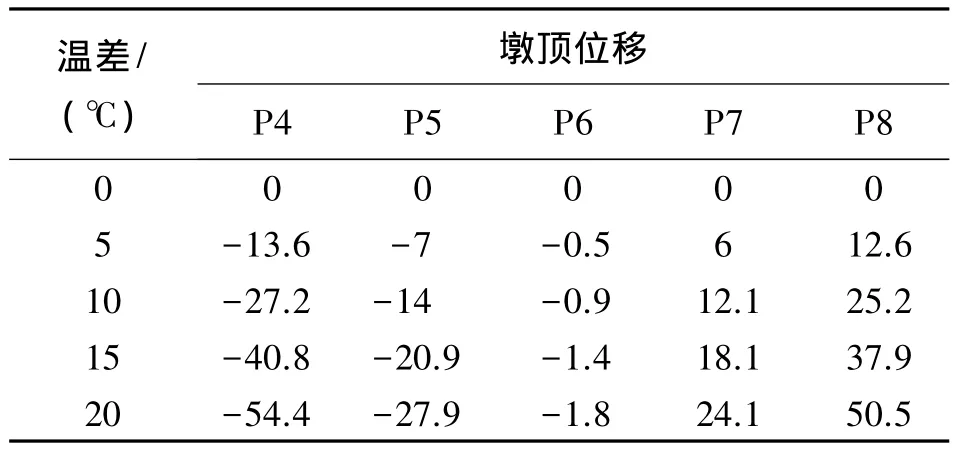
表2 不同合龍溫差對應墩頂順橋向位移 mm

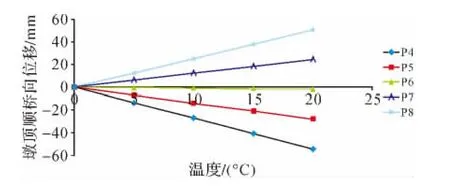
圖7 合龍溫差與墩頂位移關系圖

從圖7可以看出，各墩墩頂位移與合龍溫差基本呈線性關系，經數據擬合可知，合龍溫差每上升1℃，P4、P5、P6、P7、P8 順橋向墩頂位移分別變化－2.72 mm、－1.40 mm、－0.09 mm、1.21 mm、2.52 mm。由此可知，邊跨墩P4、P8墩頂順橋向位移受合龍溫差影響較大，中間墩P6受溫差影響最小，接近主梁縱向溫差變形的不動點。

(3)頂推量計算

根據上述數據及式(1)得合龍頂推位移，見表3。

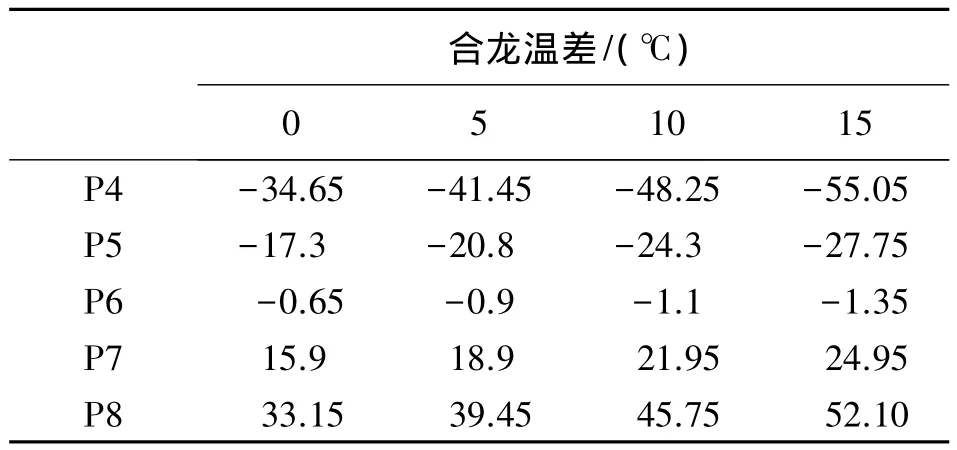
表3 不同合龍溫差墩頂頂推位移值 mm

2.頂推力計算

分別在中跨、次中跨合龍段施加100 kN作用力后，各墩所產生的位移見表4。

表4 100 kN頂推力對應墩頂位移 mm

由于頂推力與頂推位移成正比［8－10］，因此，由表4可以得到頂推力與頂推位移之間有如下關系:

墩 P4:δP4=0.057 5P;墩 P5:δP5=0.088 3P。

墩 P7:δP7=0.091 4P;墩 P8:δP8=0.041 6P。

其中，P單位為kN;順橋向位移δ單位為mm。

頂推力確定原則:由于中間墩P6受溫度及收縮徐變影響較小，故可取中跨頂推力大小相等，其大小取墩P5與墩P7頂推力之和的一半;邊跨頂推力由邊墩頂推位移量確定。

按上述頂推力計算方法，方案2下計算的各頂推力大小見表5。

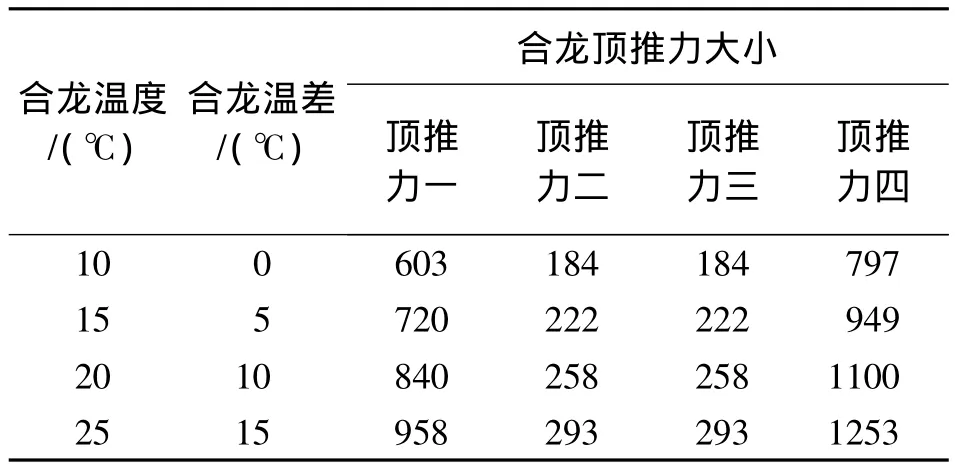
表5 方案2不同合龍溫差下施加頂推力大小 kN

對于方案3，在次邊跨施加頂推力，其頂推力大小取兩邊跨頂推力之和的一半，頂推力計算結果見表6。

取合龍理性溫度為20℃，對這3種方案進行比選。

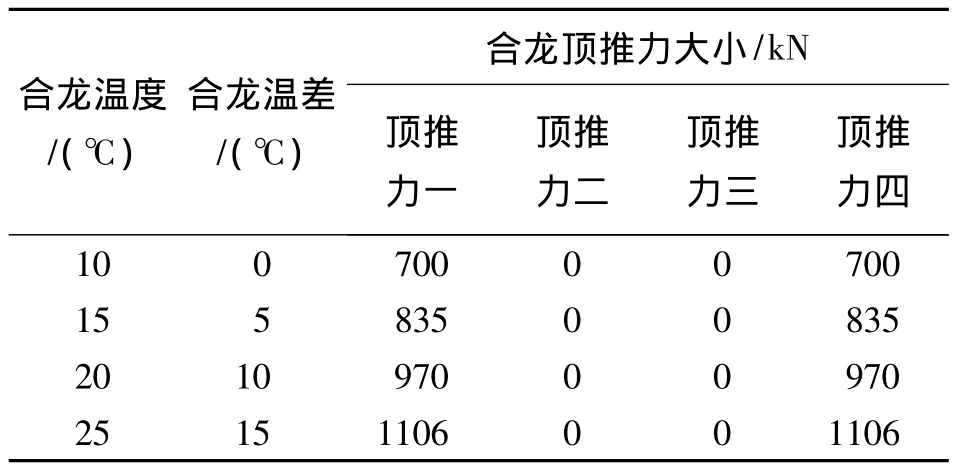
表6 方案3不同合龍溫差下施加頂推力大小

六、頂推對橋梁成橋狀態的影響

1.頂推對主梁跨中撓度的影響

3種頂推方案對成橋狀態跨中撓度的影響見表7。

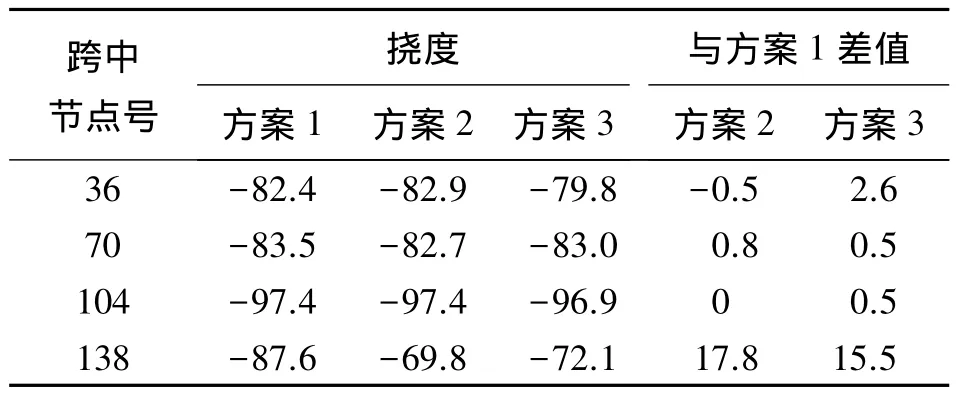
表7 頂推對主梁跨中撓度的影響 mm

表7數據表明，方案2、方案3與方案1相比，頂推后主梁跨中的撓度有所減小，即頂推后對跨中下撓問題有一定的改善。

2.頂推對墩底彎矩的影響

3種頂推方案對墩底彎矩的影響見表8。

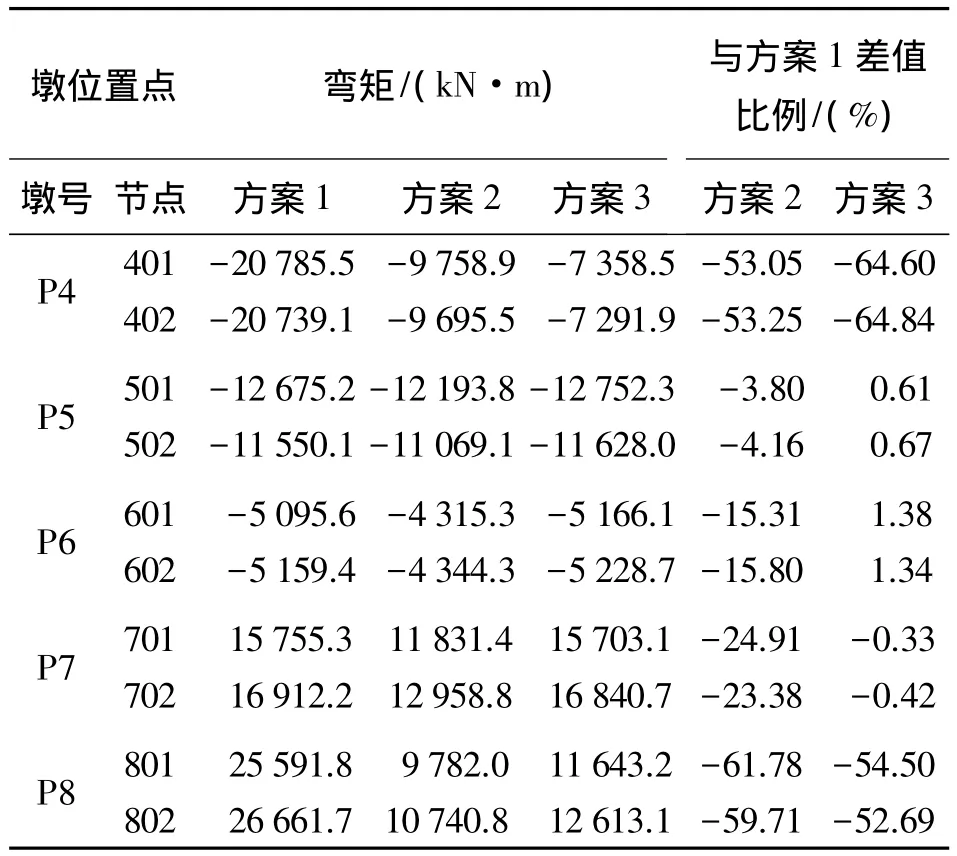
表8 頂推對墩底彎矩的影響

表8數據表明，施加水平頂推力后，各墩底彎矩有增有減，但總體趨勢是:施加頂推后，墩底彎矩呈降低趨勢。其中方案2、方案3與方案1相比，最大降低幅度分別達61.78%、64.84%。而頂推對墩P5、P6、P7墩底彎矩影響較小。

經綜合對比分析，方案2與方案3的計算結果基本一致，但方案2施加4對頂推力，施工復雜且工作量較大。因此，推薦方案3為合龍方案。

七、結 論

本文結合城川河大橋工程，提出了3種施加頂推力的合龍方案，并就各方案的頂推力大小進行了計算，通過對3種頂推方案進行對比分析，得到如下結論:

1)對于該多跨連續剛構橋頂推方案，方案2、方案3較方案1合理，頂推后能顯著減小成橋狀態下墩底彎矩。

2)通過分析比較，方案2與方案3的計算結果基本一致，但方案2施加4對頂推力，施工復雜且工作量較大。因此，推薦方案3為合龍方案。

3)通過施加適當的頂推力，減少了由合龍溫差、混凝土收縮徐變引起的主墩水平偏位，有效降低了墩底內力，對橋梁后期承載有利，同時增加了結構的安全性。

目前，該橋采用方案3已成功合龍。因此，對于多跨連續剛構橋，合龍時需考慮合龍溫差與混凝土長期收縮徐變對結構的影響，且在適當位置施加一定的頂推力是非常有必要的。

［1］范立礎.橋梁工程［M］.北京:人民交通出版社，2001.

［2］向中富.橋梁施工控制技術［M］.北京:人民交通出版社，2001.

［3］馬寶林.高墩大跨連續剛構橋［M］.北京:人民交通出版社，2001.

［4］潘國兵，劉毅.連續剛構橋主梁頂推力計算分析及合龍方案研究［J］.四川建筑科學研究院，2012，38(4):23-26.

［5］殷燦彬，王解軍，唐燦.連續剛構橋高溫合龍頂推力的計算方法研究［J］.中南林業科技大學學報，2009，29(1):111-116.

［6］鄒毅松，單榮相.連續剛構橋合龍頂推力的確定［J］.重慶交通學院學報，2006，25(2):12-15.

［7］胡清和，鄧江明，周水興.多跨連續剛構橋合龍方案研究［J］.中外公路，2009，29(3):109-114.

［8］許明雷，羅力軍.排調河一號特大橋中跨合龍頂推控制［J］.橋梁建設，2011(4):79-82.

［9］蔡軍，楊蕾，武利兵.大跨徑合龍頂推力優化計算［J］.交通科技與經濟，2013，15(1):100-102.

［10］中華人民共和國交通運輸部.JTG/TF 50—2011公路橋涵施工技術規范［S］.北京:人民交通出版社，2011.