BDS實時動態相對定位卡爾曼濾波算法

李 勝，韓永亮

(遼寧工程技術大學，遼寧阜新123000)

一、引 言

北斗衛星導航系統(BeiDou Navigation Satellite System，BDS)是中國正在實施的自主發展、獨立運行的全球衛星導航系統，其空間段包括5顆靜止軌道衛星(geostationary earth orbit satellites，GEO)和 30 顆非靜止軌道衛星(inclined geosynchronous satellite orbit，IGSO 和medium earth orbit satellites，MEO)。目前，在軌衛星14顆，其中GEO衛星5顆、IGSO衛星5顆、MEO衛星4顆，實現了亞太區域的定位、導航和授時及短報文通信服務;根據系統建設總體規劃，2020年前后，建成覆蓋全球的北斗衛星導航系統［1-2］。由于BDS已經形成了區域覆蓋，因此BDS實時動態相對定位與導航的算法和精度成為當前關注的熱點。

目前GPS實時動態相對定位算法比較成熟，得到了廣泛的應用，其方法主要是含有位置參數、速度和加速度參數，以及整周模糊度參數的濾波，濾波過程中用上一次歷元的位置、速度和加速度參數和方差通過一步轉移矩陣預測當前歷元相應的位置、速度和加速度狀態向量和方差，實現模糊度快速固定和精確位置計算［3-6］。BDS與GPS采用相同的CDMA編碼和廣播星歷樣式，并具有固定的頻率，因此兩系統的定位原理應當相同，當前BDS動態定位基本采用GPS動態定位算法，沒有充分考慮BDS的當前狀況。目前BDS在軌衛星數較少，主要是GEO和IGSO衛星，GEO衛星相對于地球靜止，衛星軌道相對于地球基本固定不變，IGSO衛星的運動周期約為24 h，測站觀測到北斗衛星的幾何構型變化較慢，歷元間的相關性較強，因此采用相同的濾波算法，BDS初始化時間明顯長于GPS。而本文提出了一種用偽距定位結果和方差陣作為位置預測值和方差陣，替換了常規的速度和加速度卡爾曼濾波中的一步轉移過程，減少了濾波狀態參數數量，縮短濾波初始化時間，濾波得到雙差模糊度浮點解和方差陣后，結合MLAMBDA方法［7-10］實時搜索固定雙差模糊度，進而得到精確的位置固定解。此濾波算法使用偽距和載波同時濾波，適用于單頻或雙頻定位，最后基于該算法對實測的BDS數據試驗進行分析，得出了BDS單頻(B1)和雙頻(B1、B2)定位精度，并對GEO和IGSO衛星的相位差分殘差值進行分析。

二、相對定位觀測方程

相對定位一般采用站間、星間差分，站間差分消除了衛星鐘差，而星間差分消除了接收機鐘差，并且由于基線距離較短，站間、星間差分有效地削弱了空間相關誤差(電離層延遲，對流層延遲，星歷誤差等)的影響，忽略多路徑的影響。其觀測方程表示如下

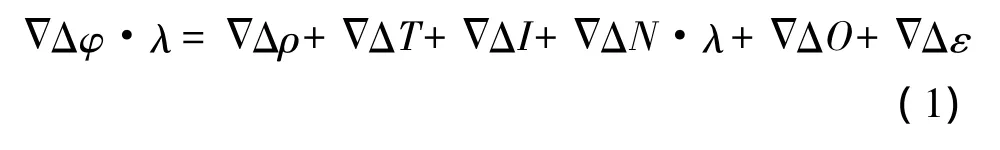
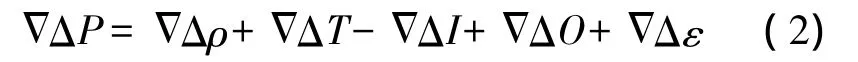
三、實時動態相對定位卡爾曼濾波

1.濾波模型

通過站間、星間差分技術消除了衛星和接收機鐘差，有效地削弱了空間相關誤差(電離層延遲、對流層延遲及星歷誤差等)的影響，忽略其殘差影響，因此相對定位觀測方程中只包含位置和整周模糊度未知數。常規動態定位通常采用加速度的濾波模型，狀態向量包括位置、速度、加速度，以及整周模糊度，其狀態方程用上一次歷元的位置、速度及加速度狀態參數預測當前歷元的位置、速度及加速度狀態參數。為了減少狀態向量的個數，實現BDS濾波的快速收斂，將常規的濾波算法中速度和加速度狀態向量去掉，濾波過程中采用偽距單點定位結果預測當前歷元的位置向量，相應的方差陣為預測位置向量的誤差方差陣，因此狀態向量只包含位置和雙差模糊度狀態參數，避免了濾波的發散。此算法適用于單頻觀測數據或雙頻觀測數據同時濾波，為了表示方便，以下僅針對B1、C展開，離散系統的卡爾曼濾波方程可以表示為

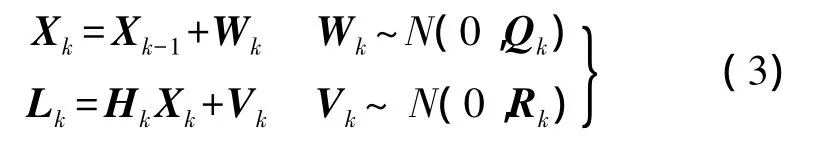
式中，狀態向量為

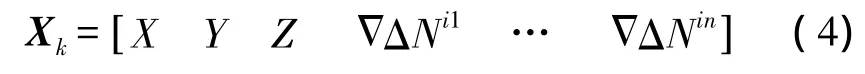
常數向量為

系數矩陣為

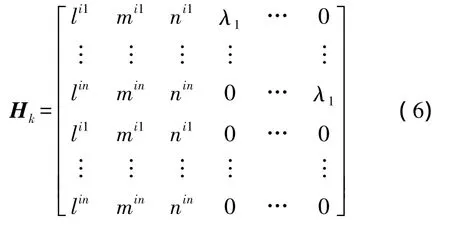
觀測噪聲陣為

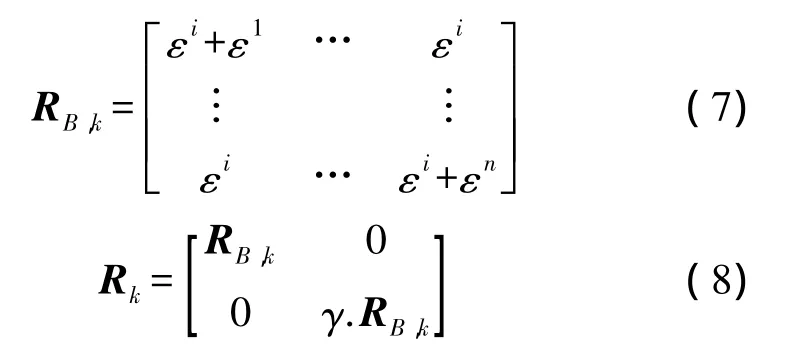
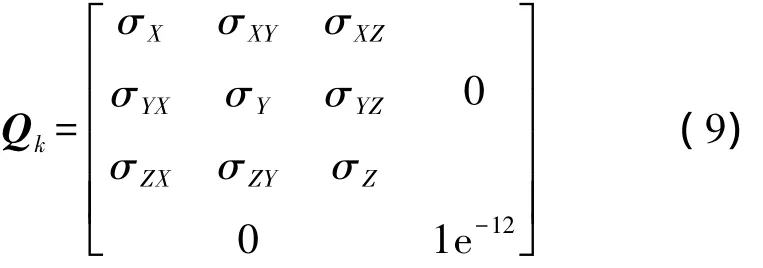
式中，i為參考衛星;n為非參考衛星數;ε為相位觀測噪聲;γ為偽距與相位精度比;l、m、n為初始位置偏導;σX、σY、σZ為偽距定位方差;σXY、σXZ、σYZ為偽距定位協方差;ΔΔN前后歷元不變，假定為零均值白噪聲。

2.第k歷元濾波過程

濾波過程中采用偽距單點定位結果預測當前歷元的位置向量，用第k歷元偽距定位結果［x，y，z］k預測位置參數，相應的方差陣為預測位置向量的方差陣，即用 k 歷元偽距定位方差陣 P［x，y，z］，k、k－1 歷元整周模糊度的濾波方差陣Pk－1和過程噪聲陣Qk計算 k歷元預測方差陣 Pk，k－1

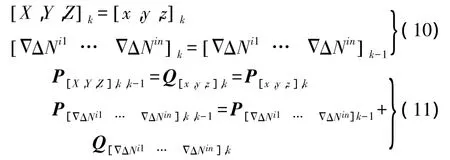
計算濾波增益陣Kk和改正數Vk，修正第k歷元預測值得到卡爾曼濾波解為

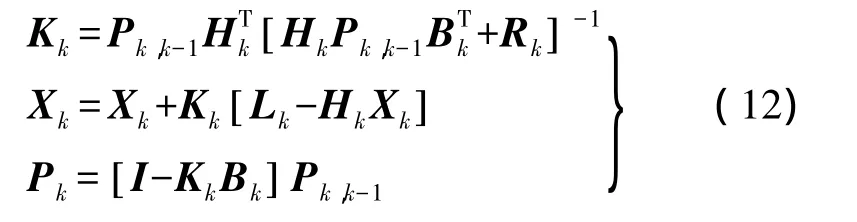
采用上述濾波算法短基線時僅需一個歷元即可正確固定整周模糊度，縮短了動態相對定位的初始化時間，濾波過程中有新生衛星升起或發生周跳，此時重新初始化模糊度，一般只需一個歷元重新固定模糊度。

四、試驗與分析

采用實測的BDS數據進行仿真動態試驗，時間為2013年9月20日8:00—12:00，地點為北京已知坐標觀測站，基線長5.6 km，采樣間隔為30 s。數據處理采用上述濾波算法進行B1和C的單頻定位試驗，再用B1、B2和C、P2進行雙頻定位試驗，衛星截止高度角15°，并對定位中誤差和GEO、IGSO衛星殘差進行分析。

1.BDS動態相對定位結果

采用上述濾波算法僅需一個歷元實現模糊度固定，圖1和圖2給出了試驗數據單頻和雙頻動態定位處理的結果，其中圖1中單頻定位精度平面E方向優于1.2 cm，N 方向優于3 cm，U 方向優于5.3 cm，點位中誤差平均約為0.8 cm;圖2中雙頻定位精度好于單頻定位主要是 N和 U方向，E方向優于1 cm，N 方向優于2.6 cm，U 方向優于4.5 cm，中誤差平均約為0.5 cm。E方向精度好于N方向主要是由衛星分布引起的，其中GEO和IGSO衛星主要分布于測站南側，而東西方向比較均勻。單頻或雙頻解算中誤差在 8.8～9.5 h 階段逐漸變大，并在 9.5 h 出現明顯的跳變，因此對衛星殘差進行分析，跳變原因將在下一節詳細分析。

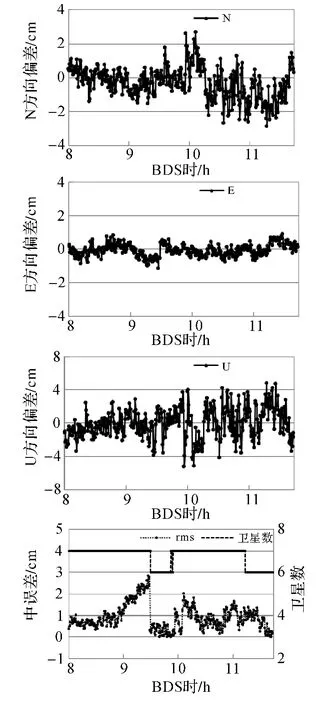
圖1 單頻相對定位結果

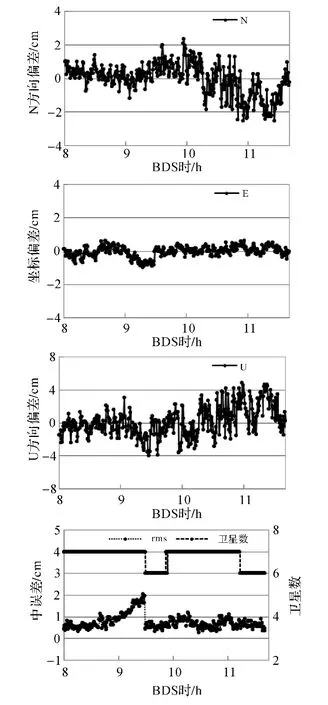
圖2 雙頻相對定位結果

2.GEO和IGSO衛星相位差分殘差

BDS系統含有 GEO、IGSO和 MEO衛星，GEO衛星相對地球位置不變，IGSO和MEO衛星相對地球作固定周期和軌道運行，因此測站坐標已知并且模糊度固定后對GEO衛星和IGSO衛星殘差進行分析，計算相位站間、星間差分殘差值(雙差相位值和幾何距離差值)，并選了 4顆衛星 PRN1、PRN4、PRN7和PRN10進行詳細分析。圖1和圖2中定位中誤差在8.8～9.5 h 階段逐漸變大并在9.5 h 出現了峰值，且衛星數相應地由7顆變為6顆，因此中誤差逐步變大應該是9.5時不參與解算衛星的殘差逐步增大引起的。

圖3顯示的PRN1和PRN4為GEO衛星，相位差分殘差值比較平穩，但B1和B2殘差值之間存在系統性偏差，PRN1的B1和B2殘差值系統差較小，約為0.5 cm，而PRN4的系統差較大，約為1 cm，主要原因是GEO衛星的位置相對于測站基本保持不變，觀測環境保持不變，B1和B2頻率造成的電離層延遲差異導致了系統性偏差;而PRN7和PRN10為IGSO衛星，相對測站位置高度角實時變化，信號傳播路徑發生變化，相位差分殘差值B1和B2互相交互，隨著高度角變小而變大，如22°時PRN7殘差值為4.5 cm，上述BDS 動態定位中誤差值8.8～9.5 h 階段逐漸變大并在9.5 h出現了峰值就是由于PRN7號衛星引起的，9.5 h后PRN7號衛星不再參與定位解算，因此中誤差急劇變小。

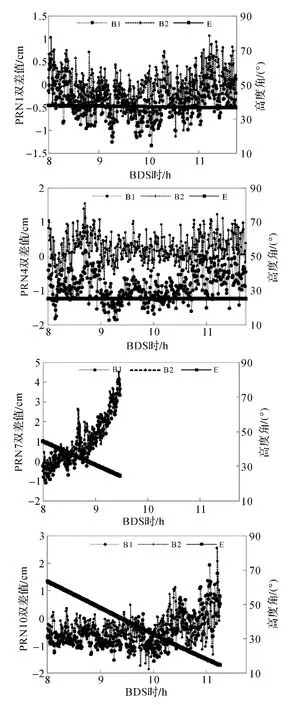
圖3 B1和B2差分殘差值

五、結 論

本文提出了一種適用于BDS的單頻或雙頻實時動態定位的濾波算法，用實測的BDS數據驗證、分析了BDS單頻和雙頻相位觀測值的定位精度，并對GEO、IGSO衛星相位差分殘差值進行了分析說明，結論主要如下:

1)采用上述動態定位算法實現單頻相對定位E方向優于1.2 cm，N方向優于3 cm;雙頻相對定位E方向優于1 cm，N方向優于2.6 cm。

2)BDS定位E方向好于N方向，原因主要是由于衛星分布集中于測站的南側，相位差分殘差值在N方向不能有效地削弱引起的。

3)GEO衛星相位差分殘差值比較平穩，但B1和B2差分殘差值之間存在電離層延遲引起的系統性偏差;IGSO衛星相位差分殘差隨著高度角變小而變大。

［1］中國衛星導航系統管理辦公室.北斗衛星導航系統發展報告(2.0 版)［R］.北京:［s.n.］，2013.

［2］GAO Z Z，ZHANG H P，HU Z G，et al.Performance Analysis of BeiDou Satellite Navigation System(4IGSO+3GEO)in Standard Positioning and Navigation［C］∥SUN J D，LIU J N，YANG Y X，et al.China Satellite Navigation Conference(CSNC)2012 Proceedings Lecture Notes in Electrical Engineering Volume 159.Berlin Heidelberg:Springer，2012:177-186.

［3］徐彥田，程鵬飛，蔡艷輝，等.估計對流層延遲的單頻RTK卡爾曼濾波算法［J］.測繪通報，2012(8):4-6.

［4］YU W K，DAI W J，DING X L，et al.Stochastic Model of GPS/BD Combined Standard Single Point Positioning［C］∥SUN J D，LIU J N，YANG Y X，et al.China Satellite Navigation Conference(CSNC)2012 Proceedings Lecture Notes in Electrical Engineering Volume 159.Berlin Heidelberg:Springer，2012:325-334.

［5］霍夫曼-韋倫霍夫，利希特內格爾，瓦斯勒.全球衛星導航系統 GPS，GLONASS，Galileo及其他系統［M］.程鵬飛，蔡艷輝，文漢江，等，譯.北京:測繪出版社，2009:100-120.

［6］徐彥田，程鵬飛，蔡艷輝.中長基線單基準站動態定位卡爾曼濾波算法研究［J］.西南交通大學學報，2013，48(2):317-322.

［7］LI C X，LIU W M.Effective GPS Positioning Algorithm with New Fast Integer Ambiguity Resolution and Kalman Filter Model［J］.Journal of Convergence Information Technology，2012，7(9):253-260.

［8］TEUNISSEN P J G.The Least-squares Ambiguity Decorrelation Adjustment:A Method for Fast GPS Integer Ambiguity Estimation［J］.Journal of Geodesy，1995，70(1-2):65-82.

［9］CHANG X W，YANG X，ZHOU T.MLAMBDA:A Modified LAMBDA Method for Integer Least-Squares Estimation［J］.Journal of Geodesy，2005，79(9):552-565.

［10］劉志平，何秀鳳，郭廣禮，等.GNSS模糊度降相關算法及其評價指標研究［J］.武漢大學學報:信息科學版，2011，36(3):257-261.