雙流體模型中人工擴散的影響數值分析

韓朋飛，郭烈錦*，李清平，姚海元，程 兵

(1. 西安交通大學動力工程多相流國家重點實驗室，陜西 西安 710049；2. 中海油研究總院，北京 100028)

雙流體模型中人工擴散的影響數值分析

韓朋飛1，郭烈錦1*，李清平2，姚海元2，程 兵2

(1. 西安交通大學動力工程多相流國家重點實驗室，陜西 西安 710049；2. 中海油研究總院，北京 100028)

研究了雙流體模型中加入人工擴散項后不同擴散項系數對模擬的影響。對于豎直管的Water Faucet問題，逐步增加人工擴散系數后非物理振蕩完全消除。對于水平管流動病態區域的工況，不采用擴散系數在中等精細度網格上計算的結果同實驗比較吻合，但無法得到網格無關解。采用Water Faucet問題確定的人工擴散系數進行計算，水動力學不穩定性被抑制，液塞頻率被低估。因此，人工擴散的量隨不同流動條件發生變化，需要具體確定。

雙流體模型；人工擴散；段塞流；數值模擬

0 引 言

管道內多相流流動模擬對石油工業的正常生產及安全保障有非常重要的意義。目前，石油開采正在向海洋尤其是深海進發，因此超長距離的管道多相混輸對管內流動的預測有著更高和更迫切的需求。

根據以往國內外的研究，一維的漂移流模型和雙流體模型是模擬預測超長距離管道流動的有力工具。漂移流模型本質上屬于混合物模型，無法對相界面上波動的發展進行預測，因此精確度有限。Lin等[1]很早就從理論上證明了雙流體模型可以預測界面上波動的發展，并且Issa等[2]也使用雙流體模型在數值模擬中捕捉到了界面波動的實時發展。因此，雙流體模型是對長距離管線流動進行準確預測的最好手段。但是，傳統的標準雙流體模型在某些區域不能保證雙曲性，界面上小的波動會被無限放大。這種特征表現在數值模擬當中，就是當網格步長不斷減小時，不斷有更小的波動被計算分辨，而計算對這些波動的放大系數不是有界的，在波長極小時趨于無窮大，從而無法得到唯一正確的收斂結果。

針對這一問題，很多學者采用各種方法進行了研究。一方面，Zanotti等[3]從純數學的角度上考慮，通過矩陣預處理實現了無條件的雙曲性，盡管對算例的模擬顯示瞬態結果也是準確的，但是理論上預處理影響了模型的瞬態項，只適用于穩態問題。另一方面，很多學者嘗試引入其他物理機制來保證雙曲性，得到了一些有用的結論。Chung等[4]發現虛擬質量力的加入并不是完全有益的，有時它會影響計算的穩定性及精確度。Holmas等[5]則指出表面張力系數作用范圍有限，人為增大表面張力系數雖然可以抑制小波長不穩定性的發展，但是這部分非物理的能量會轉移到長波里，而通過人工增加二階擴散項耗散掉不穩定的小波長波動的能量是一種合理的方法。Song等[6]通過考慮截面速度不均勻引入動量通量參數，也在廣泛的區域內得到了良態的系統。但是，Issa等[7]發現動量通量參數的預測結果同實驗偏離。他們經過同實驗的對比發現Holmas的人工擴散方法能夠在網格不斷加密的情況下得到同實驗吻合的預測結果[8]。但是，他們只對水平管的一個工況進行了研究，提出的系數對豎直管計算的作用還不清楚，需要進一步研究。

本文針對目前保持雙流體模型雙曲性的研究，對雙流體模型模擬豎直管內的流動進行探索，尋求獲得正確預測結果所需人工擴散項系數，并驗證此組系數計算水平管段塞流時的精確度。

1 控制方程

加入人工擴散項后的一維雙流體模型如下：

(1)

(2)

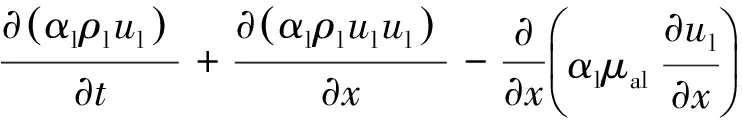
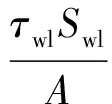
(3)

(4)

αl+αg=1，

(5)

式中：下標l和g分別表示液相和氣相；下標w和i分別表示在壁面處和相界面處；α表示相含率；ρ表示密度；u表示速度；p表示壓力；g表示重力加速度；hl表示液膜厚度；τ表示切應力；θ表示管道傾角；S表示濕周；A表示管道橫截面積。氣相為理想可壓縮氣體，液相為不可壓縮流體。

式(1)～(4)左邊第三項二階偏導即為加入的人工擴散項，φal和φag分別表示液相和氣相連續方程的人工擴散項系數，μal和μag分別表示液相和氣相動量方程的人工擴散項系數。剪切應力的表達式如下：

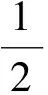
(6)

式中：f為Fanning摩擦系數；兩相的相對速度ur=ug-ul。

對于水平管和豎直管，兩相的濕周計算分布如圖1所示。

圖1 濕周及兩相分布示意圖Fig.1 Schematic representation of wetted perimeters and two-phase distributions

水平管相界面上的摩擦系數采用Taitel-Dukler模型[9]：

(7)

豎直管相界面上的摩擦系數采用Wallis[10]的模型：

(8)

D為管道直徑。水平管氣相與壁面間的摩擦系數同樣采用Taitel-Dukler的模型[9]：

(9)

水平管液相與壁面間的摩擦系數采用Spedding-Hand模型[11]：

(10)

豎直管液相與壁面間的摩擦系數采用Wallis模型[10]：

(11)

雷諾數的表達式為

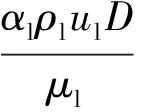
(12)

2 數值方法

氣液相的連續和動量方程式(1)～(4)通過有限體積法在同位網格上進行求解，采用Rhie-Chow插值以消除壓力速度的失耦。壓力修正方程采用兩相混合的質量守恒方程導出，其形式如下：

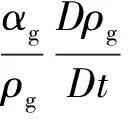
(13)

式中：D/Dt為所給量的物質導數。

為了提高計算的穩定性，時間離散格式為一階歐拉隱式后向差分，空間離散格式采用二階迎風。為了保證計算收斂性，壓力與速度的耦合采用SIMPLE算法，并設定全局最大Courant數為0.1，根據Courant數自動選取時間步長，計算收斂的判據為1×10-6。

3 結果及討論

3.1 Water Faucet問題

Water Faucet問題是檢驗數值計算結果精確度的常用標準方法，其過程如圖2所示。其結構為一段12 m長、內徑為1 m的豎直管道，上部入口含氣率為0.2，氣相和液相的速度分別為0和10 m/s，出口壓強固定為105Pa。氣相的密度為1.16 kg/m3，液相的密度為1 000 kg/m3，整個系統的溫度固定為50 ℃。此問題的解析解為

(14)

.

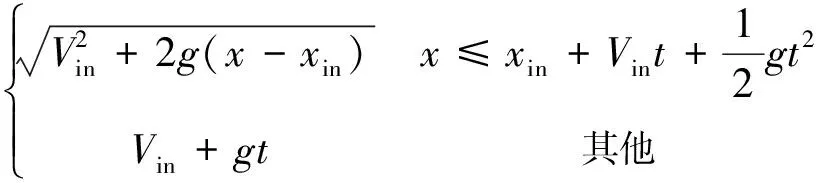
(15)

當采取不同的擴散項系數和網格控制容積(cv)數量時，模擬得到的t=0.5 s和t=2.5 s時的結果和解析解的結果對比分別如圖3和圖4所示。從圖3可以看出，當未引入人工擴散時，雙流體模型是不穩定的病態問題，網格密度為500 cv時，含氣率曲線在梯度劇變處發生了大幅振蕩。而如圖4顯示，未引入人工擴散的計算并不能得到穩定的穩態結果。

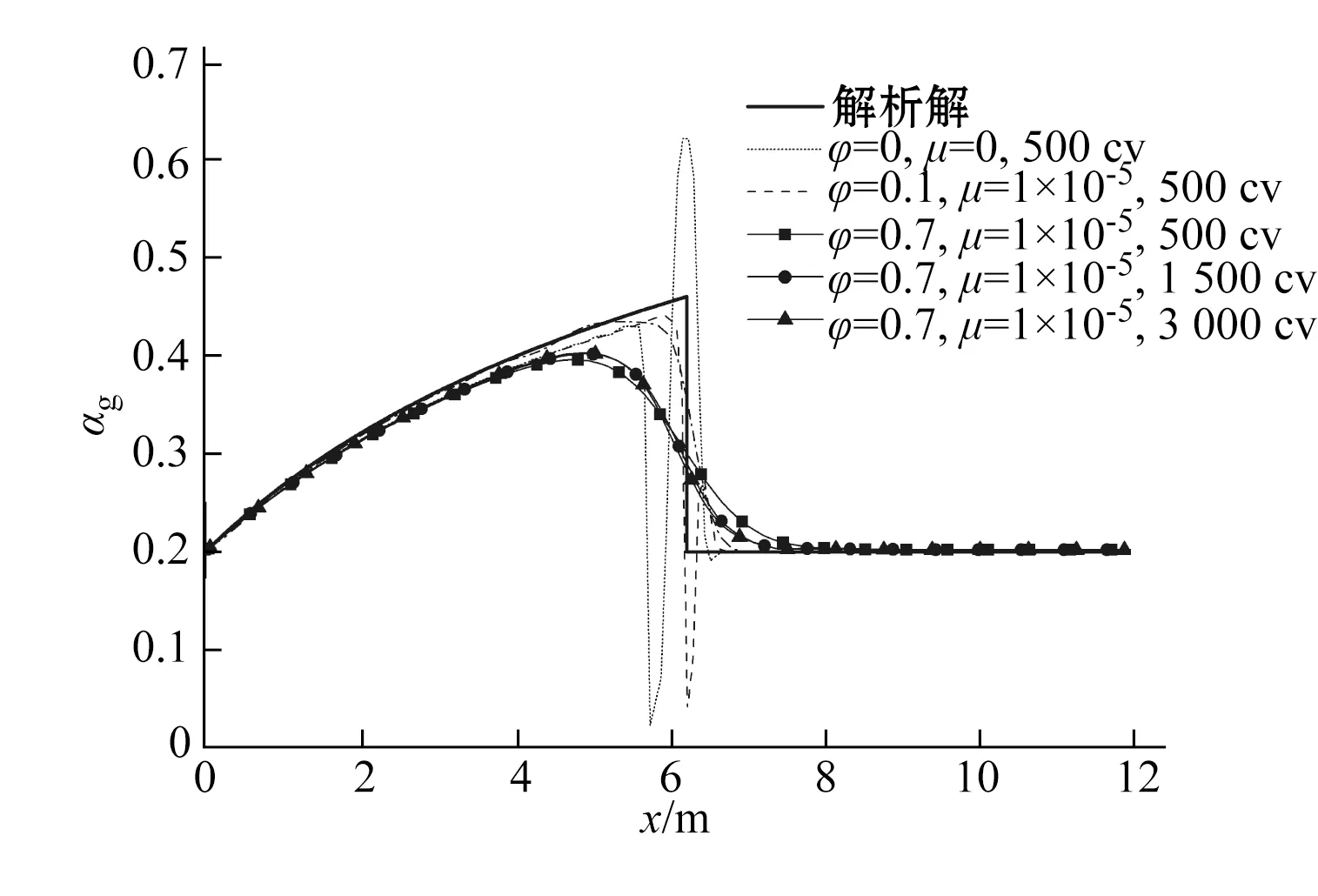
圖3 不同擴散項系數及網格密度在t=0.5 s時模擬與解析解比較Fig.3 Comparison of simulation and analytical results for different diffusion coefficients and mesh densities at t=0.5 s

圖4 不同擴散項系數及網格密度在t=2.5 s時模擬與解析解比較Fig.4 Comparison of simulation and analytical results for different diffusion coefficients and mesh densities at t=2.5 s

當擴散系數采用Issa等[8]的系數時，含氣率的非物理振蕩已被減弱但尚未消失。若進一步增大動量擴散系數，計算沒有明顯的改善，因此逐步增大質量擴散系數。質量擴散系數從0.1開始逐步增大時的計算結果與解析解的比較如圖5所示。從圖中可從看到隨著質量擴散系數的逐步增大，非物理波動的幅度逐漸減小；當質量擴散系數達到0.7時，計算結果已經不存在非物理振蕩。雖然由于擴散的影響，含氣率的曲線變得更加平滑，但是能夠得到符合物理過程的無振蕩解，損失的精度是可以接受的。當網格密度進一步加密到1 500 cv和3 000 cv時，仍舊沒有非物理振蕩出現，可以認為此時能夠得到所求解問題的網格無關解。

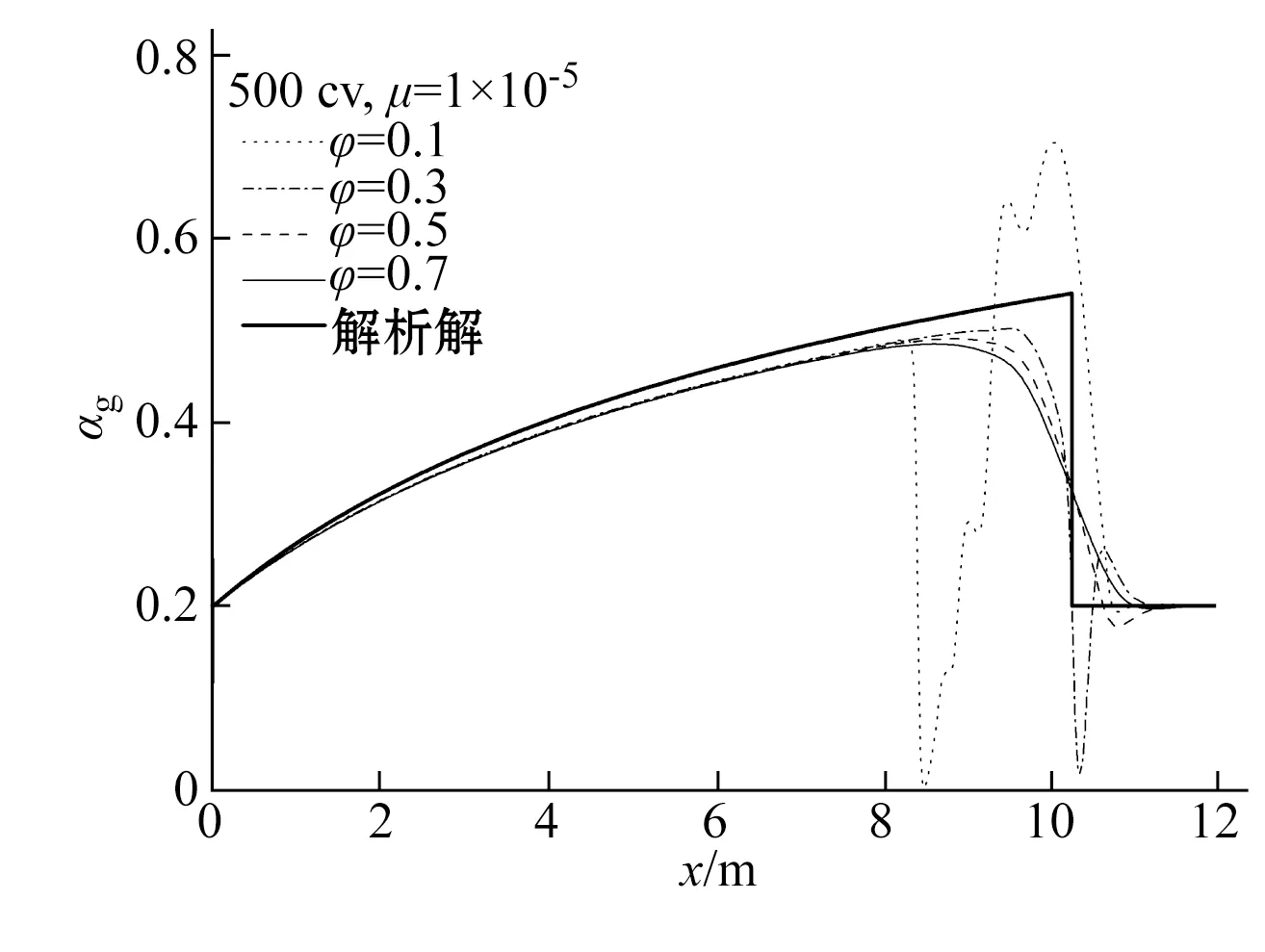
圖5 不同質量擴散項系數在t=0.75 s時模擬與解析解比較Fig.5 Comparison of simulation and analytical results for different diffusion coefficients at t=0.75 s

3.2 水平管段塞流

Woods等[12]列舉的內徑為0.095 m水平管內各種表觀氣速uSG和表觀液速下uSL的段塞流液塞頻率如圖6所示。本文選取了氣液相入口表觀速度分別為15.9 m/s和1.2 m/s遠離穩定邊界的病態區域工況，分別使用較粗網格不加入人工擴散和人工擴散系數φ=0.7，μ=1×10-5進行計算。

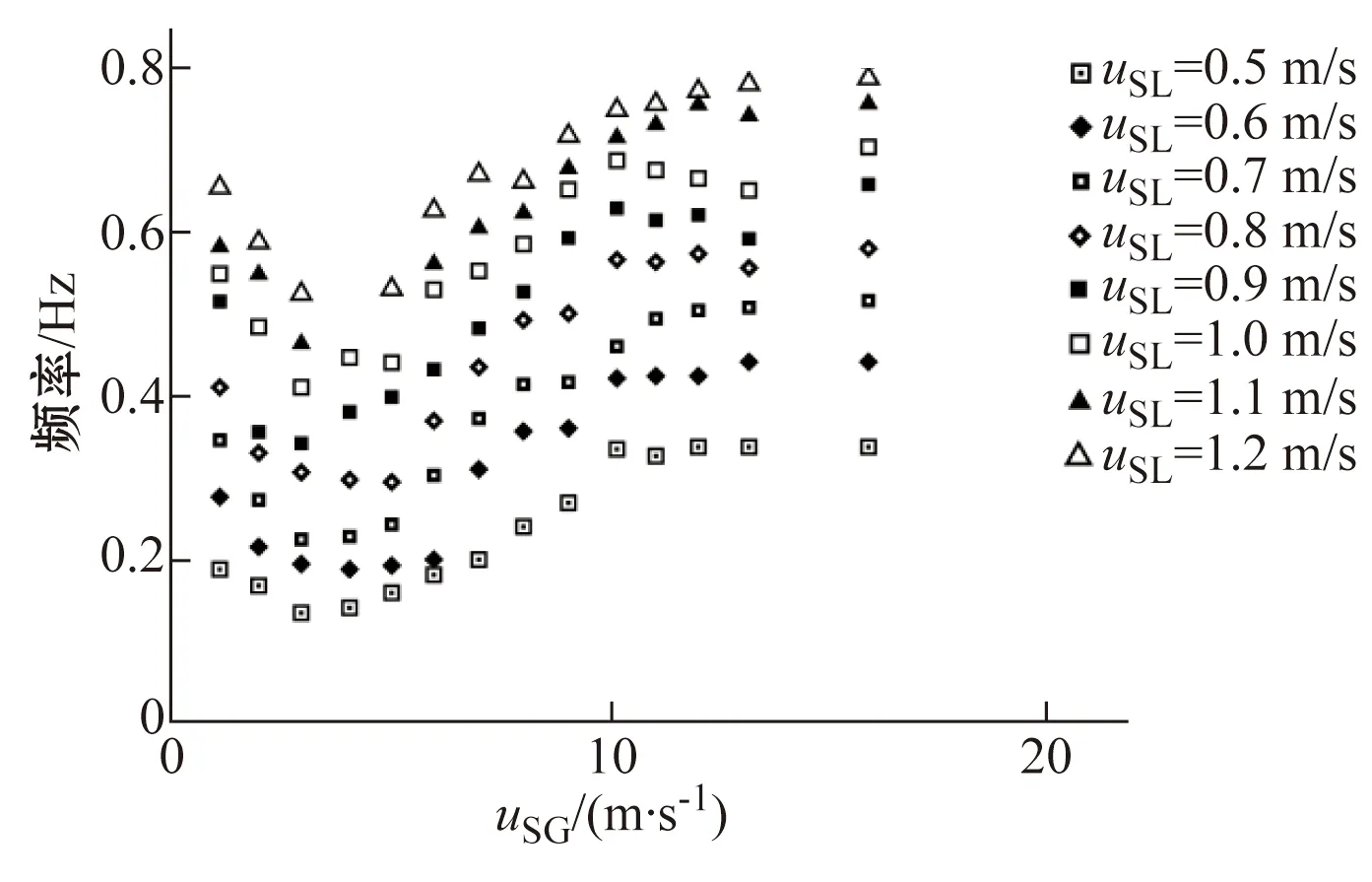
圖6 Woods等[2]列舉的液塞頻率實驗數據Fig.6 Experimental data for slug frequency presented by Woods et al[12]

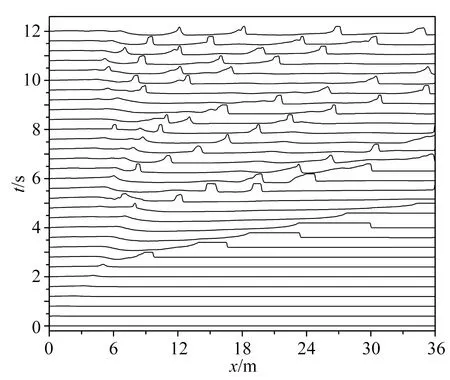
圖7 模擬得到的沿管道無量綱液位高度隨時間的變化(φ=μ=0)Fig.7 Time trace of simulated non-dimensional liquid film height along the pipe (φ=μ=0)

在網格密度為1 500 cv時，計算得到的無量綱液位高度(hl/D)的瞬態曲線隨時間的變化如圖7所示，圖中相鄰曲線間的時間間隔為0.4 s。計算初始狀態管道內無量綱液位高度為均勻的0.5，隨著氣液間相互作用的發展，約2 s時相界面的波動開始出現并在約3 s時發展為液塞。由于初始條件設置，液塞前面的液膜厚度較大，液塞長度能夠不斷增長，因此需等第一個長液塞流出后才能反映真實的流動。從后續的發展曲線來看，并未出現此種超長的液塞。在第一個超長液塞流出管道后，統計得到的液塞頻率為0.88 Hz，與0.79 Hz的實驗結果相比，誤差為11.4%。雖然計算結果同實驗相比很接近，但是當加密網格后，進一步被解析的短波波動使得計算很快發散，無法得到網格獨立解。

采用前文驗證的擴散系數在網格密度為3 000 cv的細網格上進行模擬，得到的無量綱液位高度的瞬態曲線隨時間的變化如圖8所示。從圖8可以看出，液面高度的波動被抑制，曲線變得平滑，液塞形成的頻率降低，統計得到的液塞頻率降低為0.58 Hz，與實驗相比減小了26.5%，顯然此時人工擴散量是過大的。但是，進一步加密網格未能顯著改善預測結果，證明人工擴散量在精細網格上仍舊過大，得到的收斂結果對液塞頻率的預測偏低。可以預測當擴散量很大時，雙流體模型的性能類似于混合物模型。

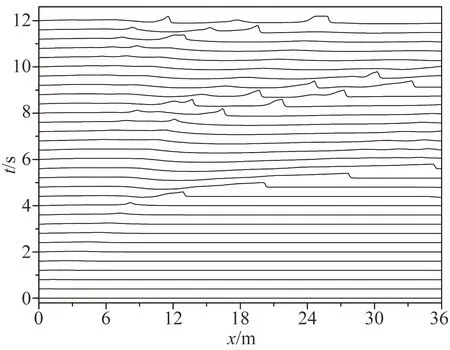
圖8 模擬得到的沿管道無量綱液位高度隨時間的變化(φ=0.7,μ=1×10-5)Fig.8 Time trace of simulated non-dimensional liquid film height along the pipe(φ=0.7,μ=1×10-5)

4 結 語

通過加入人工擴散可以使雙流體模型在原本病態的區域內轉變為良態問題。經過一系列的數值實驗，得出在人工擴散項系數為φ=0.7，μ=1×10-5時，豎直管Water Faucet問題非物理振蕩完全消失。對于水平管內流動病態區域的工況，φ=0.7，μ=1×10-5時水動力學不穩定性被抑制，液塞頻率降低。水平管人工擴散項的系數需要根據不同工況決定，有待進一步研究。

[1] Lin P Y, Hanratty T J. Prediction of the initiation of slugs with linear stability theory[J]. International Journal of Multiphase Flow, 1986, 12(1): 79.

[2] Issa R I, Kempf M H W. Simulation of slug flow in horizontal and nearly horizontal pipes with the two-fluid model[J]. International Journal of Multiphase Flow, 2003, 29(1): 69.

[3] Zanotti A L, Méndez C G, Nigro N M, et al. A preconditioning mass matrix to avoid the ill-posed two-fluid model[J]. Journal of Applied Mechanics, 2007, 74(4): 732.

[4] Chung M-S, Lee S-J. A modified semi-implicit method for a hyperbolic two-fluid model[J]. Appl Numer Math, 2009, 59(10): 2475.

[5] Holmas H, Sira T, Nordsveen M, et al. Analysis of a 1D incompressible two-fluid model including artificial diffusion[J]. IMA Journal of Applied Mathematics, 2008, 73(4): 651.

[6] Song J H, Ishii M. The well-posedness of incompressible one-dimensional two-fluid model[J]. International Journal of Heat and Mass Transfer, 2000, 43(12): 2221.

[7] Issa R I, Montini M. Applicability of the momentum-flux-parameter closure for the two-fluid model to slug flow[C]. 6th International Symposium on Multiphase Flow, Heat Mass Transfer and Energy Conversion, 2009: 712.

[8] Issa R I, Montini M. The effect of surface tension and diffusion on one-dimensional modelling of slug flow instabilities[C]. 7th International Conference on Multiphase Flow, 2010.

[9] Taitel Y, Dukler A E. A model for predicting flow regime transitions in horizontal and near horizontal gas-liquid flow[J]. AIChE Journal, 1976, 22(1): 47.

[10] Wallis G B. One-Dimensional Two-Phase Flow[M]. New York: McGraw-Hill,1969.

[11] Spedding P L, Hand N P. Prediction in stratified gas-liquid co-current flow in horizontal pipelines[J]. International Journal of Heat and Mass Transfer, 1997, 40(8): 1923.

[12] Woods B, Fan Z, Hanratty T. Frequency and development of slugs in a horizontal pipe at large liquid flows[J]. International Journal of Multiphase Flow, 2006, 32(8): 902.

NumericalAnalysisoftheEffectofArtificialDiffusionTermsonTwo-FluidModel

HAN Peng-fei1, GUO Lie-jin1, LI Qing-ping2, YAO Hai-yuan2, CHENG Bing2

(1.StateKeyLaboratoryofMultiphaseFlowinPowerEngineering,Xi’anJiaotongUniversity,Xi’an,Shaanxi710049,China; 2.CNOOCResearchInstitute,Beijing100028,China)

When artificial diffusion terms are introduced in two-fluid model, the effects of different artificial diffusion coefficients are studied. For vertical pipe Water Faucet problem, when the artificial diffusion coefficients are gradually increased, nonphysical oscillations can be eliminated. For horizontal pipe flow in ill-posed region， the calculated results without diffusion terms agree with experimental data but the mesh independent solution cannot be obtained. When the coefficients calibrated in Water Faucet problem are adopted, hydrodynamic instability is suppressed to some extent and slug frequency is underestimated. Therefore, the amount of artificial diffusion varies with different flow conditions and should be determined specially.

two-fluid model; artificial diffusion; slug flow; numerical simulation

O359

A

2095-7297(2015)01-0023-05

2014-12-29

國家科技重大專項(2011ZX05026-004-02)、國家自然科學基金重點項目(51236007)

韓朋飛(1983—),男，博士研究生，主要從事氣液兩相流方面的研究。

*通信作者